特征点检测

角点检测——FAST

若某像素与周围领域内足够多的像素点相差较大，则该像素可能是角点。

检测步骤

1. 1. 1. 以一个像素p为中心，取半径为3的圆上的16个像素点。
      2. 计算p1，p5，p9，p13像素与中心像素的差（绝对值），若其中至少有3个超过阈值，则可能是角点，进一步检测；否则直接结束
      3. 计算p1到p16所有像素点与中心点的像素差，若至少有连续9个超过阈值，则是角点；否则不是角点
      4. 计算完所有角点，进行非极大值抑制，若某个角点3x3或5x5范围内，自己是最大的，则自身保留，否则放弃该角点。

python实现

def FASTGetRadius(y,x):
    P = []
    for indexX in range(x-1,x+2):
        P.append([y - 3,indexX])
        P.append([y + 3, indexX])

    for indexY in range(y-1,y+2):
        P.append([indexY,x-3])
        P.append([indexY, x+3])

    P.append([y - 2,x - 2])
    P.append([y - 2, x + 2])
    P.append([y + 2, x - 2])
    P.append([y + 2, x + 2])
    return P
def FASTGetScore(y,x,P,img):
    score = 0
    for point in range(0,len(P)):
        score+= np.abs(img[P[point][0],P[point][1]]-img[y,x])
    return score
def FAST(img,T):
    img = np.float32(img) #原本是短整型只能存储0-255，当出现负值时会溢出，因此不能用于差值运算
    height,width = img.shape[0],img.shape[1]
    corner = []
    for y in range(3,height-3):
        for x in range(3,width-3):
            count=0
            if np.abs(img[y-3,x]-img[y,x]) >= T:
                count+=1
            if np.abs(img[y,x-3]-img[y,x]) >= T:
                count+=1
            if np.abs(img[y+3,x]-img[y,x]) >= T:
                count+=1
            if np.abs(img[y,x+3]-img[y,x]) >= T:
                count+=1
            if count<3:
                continue
            P = FASTGetRadius(y,x)
            count=0
            for point in range(0,len(P)):
                if np.abs(img[P[point][0],P[point][1]]-img[y,x]) >= T:
                    count+=1
                    if count>=9:
                        break
            if count<9:
                continue
            corner.append([y,x,P])
    #非极大值抑制
    panel = np.zeros((img.shape),dtype=np.float32) #创建全0模板
    for item in corner:#在模板上计算每个点的score
        panel[item[0],item[1]] = FASTGetScore(item[0],item[1],item[2],img)
    window=3
    for item in corner:#在模板上对每个特征点进行非极大值抑制。
        isContinue=True
        for y in range(item[0]-window//2,item[0]+window//2+1):
            for x in range(item[1] - window // 2, item[1] + window // 2 + 1):
                if (panel[y,x]>panel[item[0], item[1]]):
                    panel[item[0], item[1]]=0
                    isContinue=False
                    break
            if isContinue==False:
                break
    for y in range(0,height):
        for x in range(0,width):
            if panel[y,x]>0:
                P = FASTGetRadius(y, x)
                for point in P:
                    img[point[0], point[1]] = 0

    plt.imshow(img,cmap="gray")
    plt.show()

优点

速度快

缺点

特征点不具有方向

不满足尺度不变性

 

 

 

斑点检测——LoG（Laplace of Gaussian）

基本思想

LoG对指定宽度斑点进行卷积时，参数中，取不同的σ响应幅值会不同，取响应幅值最大时候的σ用于检测该宽度的斑点。如下图（已经做了尺度归一化）。

一维形式如下：

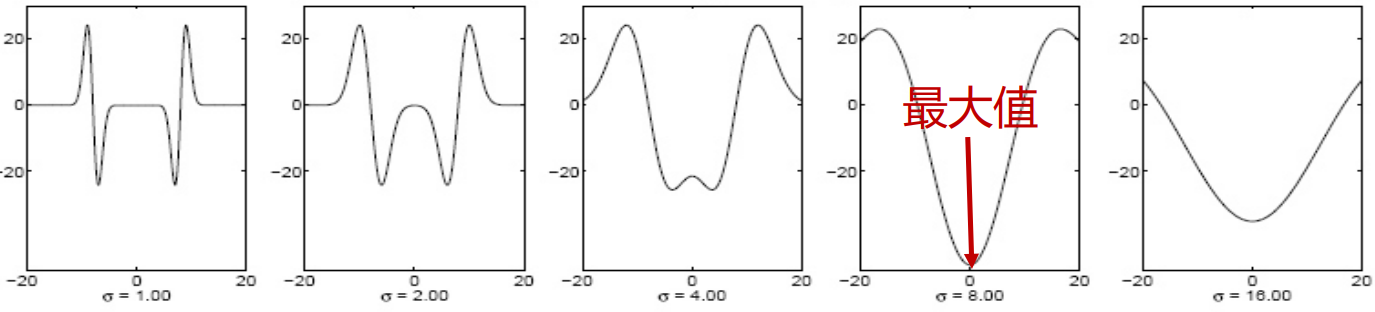
二维形式如下：

    

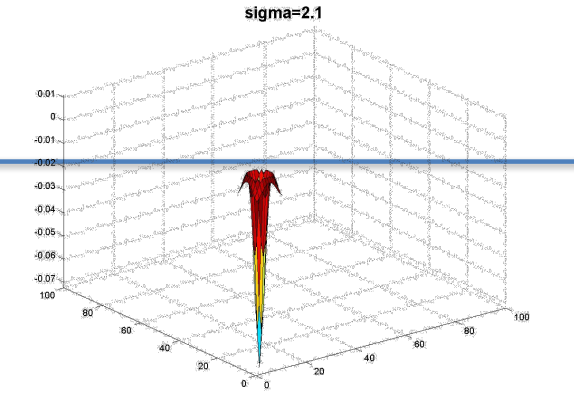
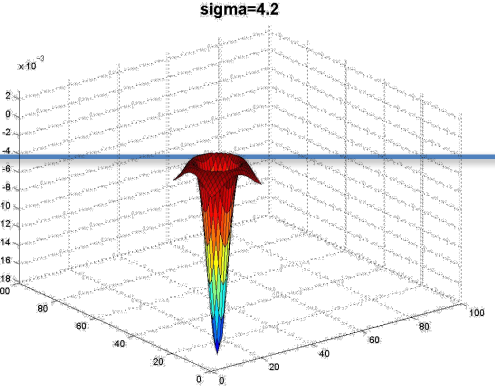
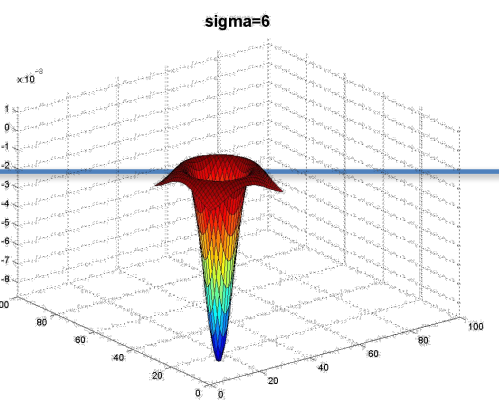
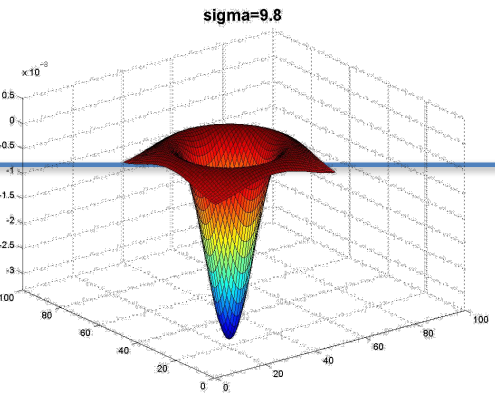
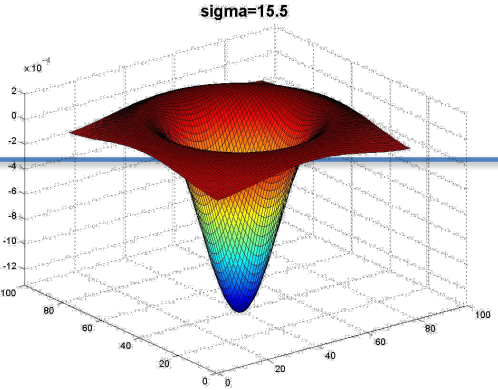
σ取不同的值，在一副图片中检测到的斑点尺寸也不同

响应幅值最大的尺度也叫做“本征尺度”。

LoG就是高斯函数的拉普拉斯算子，对高斯函数求二阶微分算子。

拉普拉斯算子

高斯拉普拉斯

斑点

边缘点是像素的阶跃，而斑点是两个阶跃之间的区域。

以二值图像为例

尺度归一化

尺度归一化的原因

不同尺寸的斑点，用相同LoG卷积结果

如下图所示，当LoG函数的σ=1时，遇到-1到1宽度的阶跃区间时，响应幅值最大，说明σ=1时适合检测半径为1大小的斑点。

相同尺寸的斑点，用不同LoG卷积结果

对于想要检测的斑点，可以调整σ来寻找响应最大的尺度。

根据LoG的公式：

可知当σ越大，LoG越小，因此要检测大的斑点，不做尺度归一化，会导致响应幅值特别小以致于难以检测。

如下图所示，LoG的尺度σ越大，LoG算子的最大幅度逐渐减小，导致响应最终难以检测，因此需要做尺度归一化。

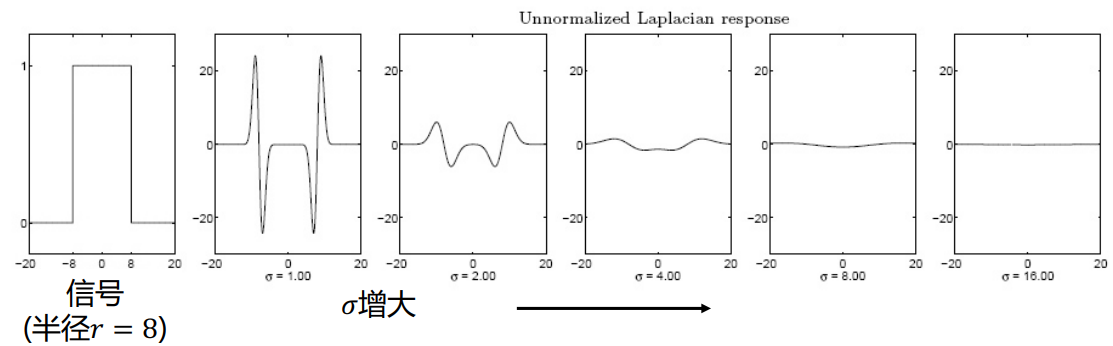
尺度归一化的LoG

对LoG算子变形，得到如下形式

两边同时乘以σ²，得到尺度归一化的LoG：

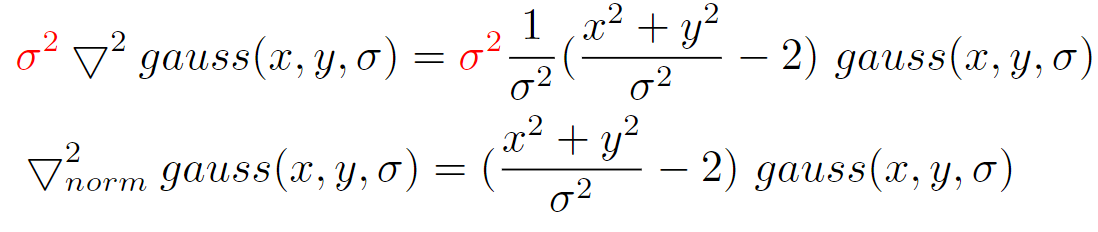
已知要检测斑点的半径，确定尺度σ

要使得响应幅值最大，则要将LoG的过零点和圆的直径对齐

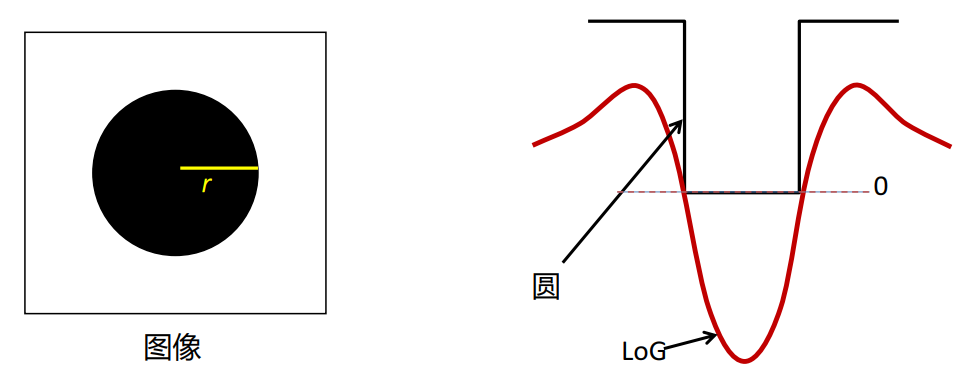
           标准圆的方程：

代入尺度归一化的LoG，并求LoG在过零点位置的σ

得到：

   

斑点检测——DoG（Difference of Gaussian）

基本思想

DoG是LoG的近似，用于加速计算。高斯差分采用两个不同的σ之差进行运算。

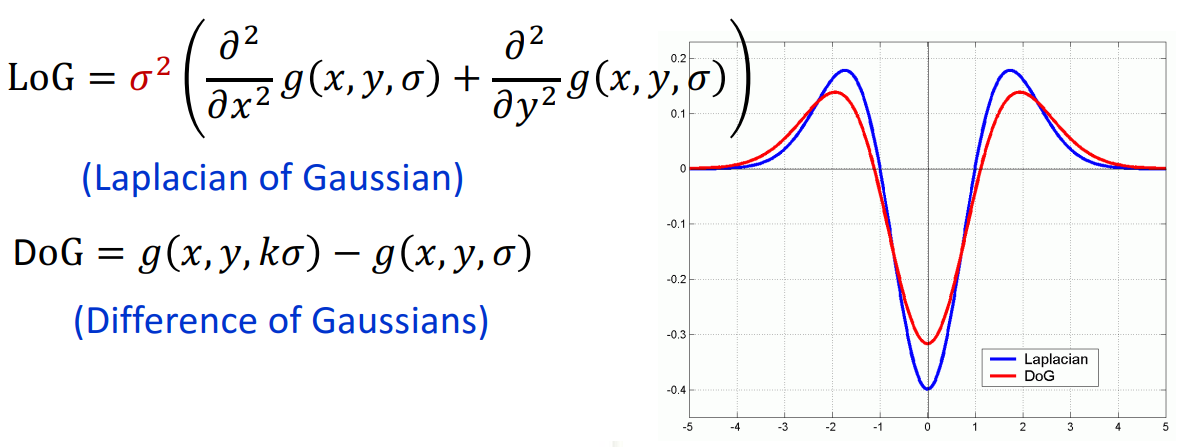
LoG和DoG的关系

高斯函数在σ上的变化率为：

高斯差分描述的是高斯函数取两个不同尺度的σ之差，不是变化率。

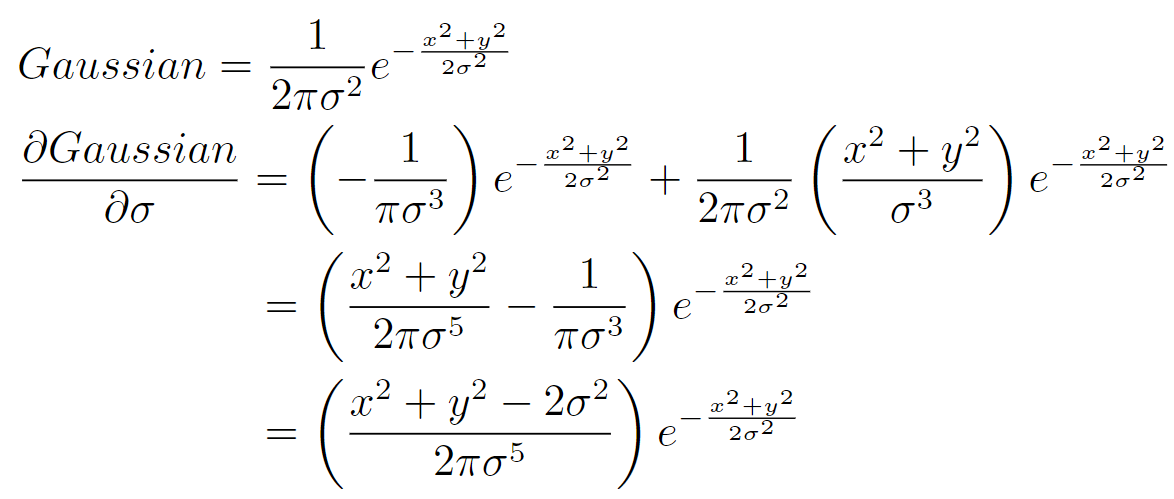
高斯拉普拉斯算子的变形为：

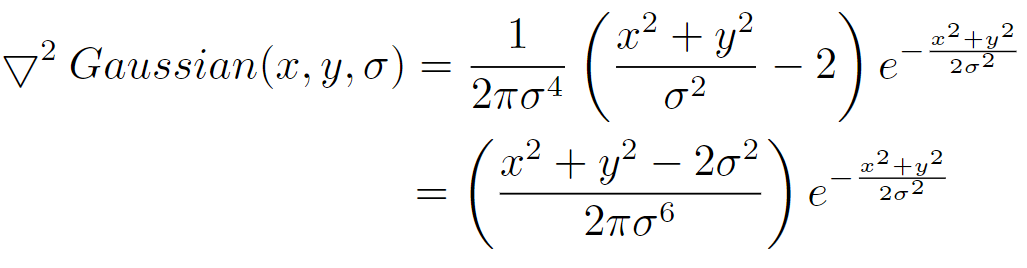
其与高斯函数对σ的导数的关系为：

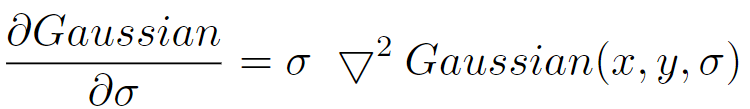
而根据导数定义，高斯函数对σ的导数可以近似为：

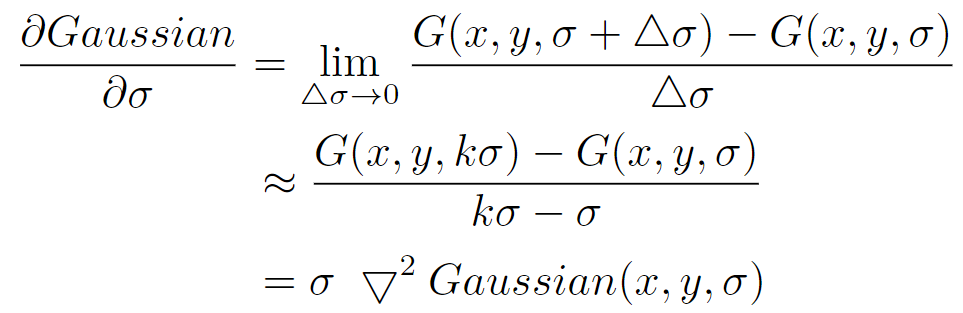
将最后等式变形，得到高斯差分DoG和LoG的关系：

即：

其中k-1是常量，通常取根号2

DoG检测斑点步骤

构造高斯金字塔

构造高斯差分金字塔

极值点定位

 

SIFT算法

构造高斯金字塔

对图像进行高斯平滑处理，然后下采样，反复多次，形成高斯金字塔。

高斯金字塔结构为先分成多个八度，每个八度内再分多个层。

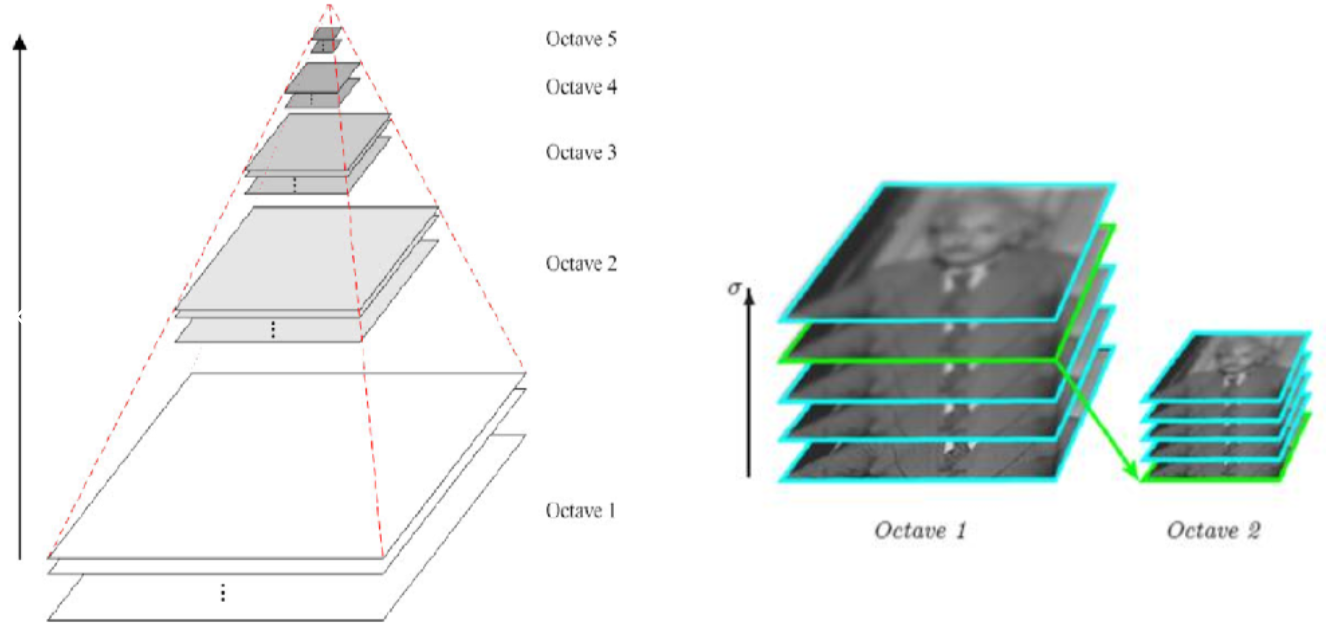
假设图像大小为512 x 512，则可以分为log₂512 = 9 -3 = 6组，每组3层。

第0层先把图像扩大2倍。

每组内，的尺度分别为2^oσ,2^okσ,2^ok²σ,...2^okⁿσ。其中o是第o个八度。

第0层内，I*G(x,y,σ)，I*G(x,y,kσ)，I*G(x,y,k²σ)

第1层内，I*G(x,y,2σ)，I*G(x,y,2kσ)，I*G(x,y,2k²σ)

第2层内，I*G(x,y,4σ)，I*G(x,y,4kσ)，I*G(x,y,4k²σ)

...

第6层内，I*G(x,y,64σ)，I*G(x,y,64kσ)，I*G(x,y,64k²σ)

同组内，图像尺度关系

相邻组之间，对应层之间的尺度关系

构造高斯差分金字塔提取特征

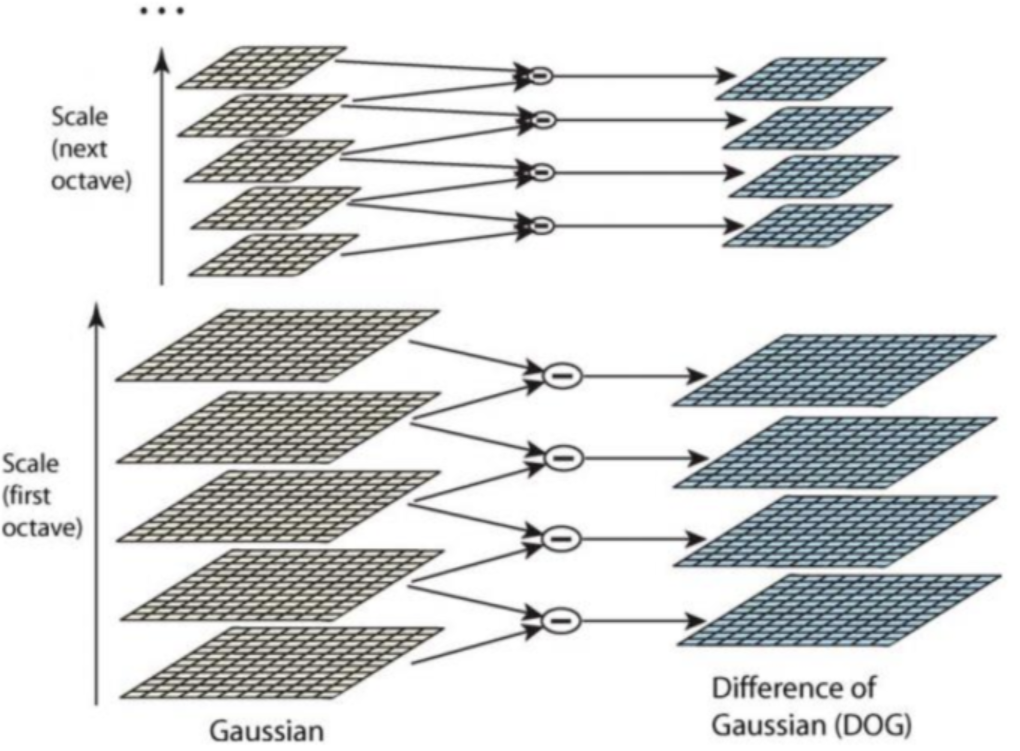
每个八度内，相邻层两两相减，即完成了高斯差分操作，提取到了特征点。回想DoG出现的目的就是使用不同尺度的高斯函数进行相减，得到近似LoG的效果。

 

局部极值点检测

每一个点要分别与以自身为中心的9宫格，和上下两个尺度的9宫格所有特征点进行比较，一共要比较26个点。

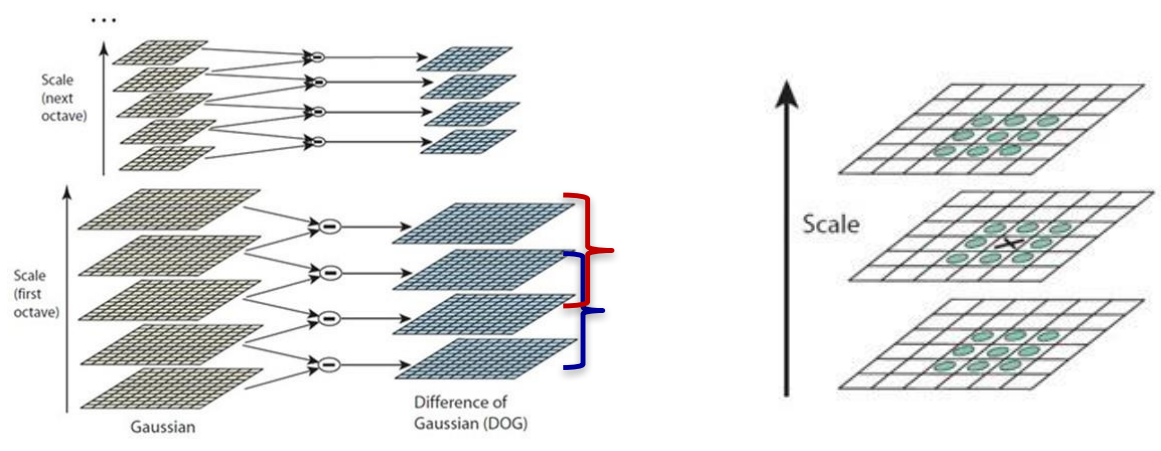
假设每个八度之间有4层高斯差分金字塔，那么只能在中间两层进行差分。

这样产生的极值点并不全都是稳定的特征点，因为某些极值点响应较弱，而且DoG算子会产生较强的边缘响应。

关键点精确定位

原因

使用DoG检测到的极值是离散的极值，且在高斯金字塔进行下采样时，像素逐渐向粗粒度转变，所检测到的极值也是粗粒度的极值。

问题描述

给定已知的粗粒度离散的极值点，需要估算出细粒度的极值点。

解决方案

可以使用泰勒公式逼近原函数，任意给定一个H，泰勒公式都可以在该点处进行多项式展开，近似原函数。

得到该近似函数，求导得到该函数的极值点。

若求得极值点与原极值点偏移量大于0.5，则在下一个离散的点进行泰勒展开，直到收敛。

为什么是0.5?

如下图所示，红色为真实的极值点，绿色为离散的极值点。所有的离散值中，x(1)最大，但是真实极值里x(5)最近。

首先在X(1)处展开，求得极值与x(1)的偏移量ΔX>0.5，则跳到x(2)处展开，到了x(4)处展开，偏移量ΔX仍然大于0.5，也就是过了4.5这个点，这就与X(5)更近。

在X(5)处展开，真实极值位置在4.5到5之间，偏移量肯定小于0.5。求该点极值即可。

 

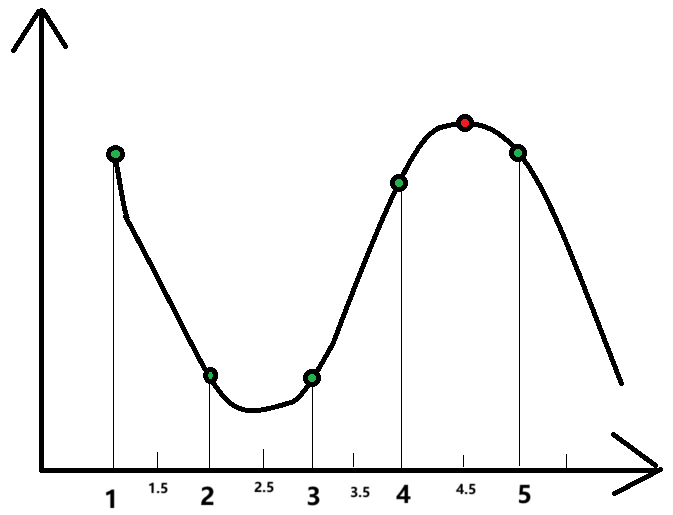
迭代逼近，求里极值最近的离散点

DoG在检测到的粗粒度极值点H处的二阶泰勒展开式为：

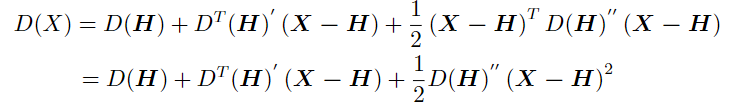
对其求导，并令其等于0：

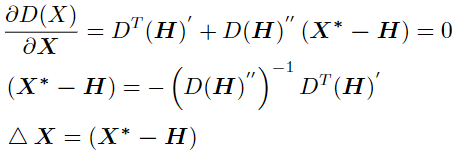
其中X*是极值点，H是原极值点，两者之差为粗粒度极值点与真实极值点的偏差，记ΔX。

所以当ΔX>0.5时，就在H+1位置进行泰勒展开，求极值，直到收敛。

离散点中，某一点一阶导数D(H)'和二阶导数D(H)''可以用差分法，根据前后两个点来获得。

迭代结束，求极值

至此，偏移量已经收敛到了0.5以下，可以将最近的极值点H_Nearest代入泰勒公式求得极值。

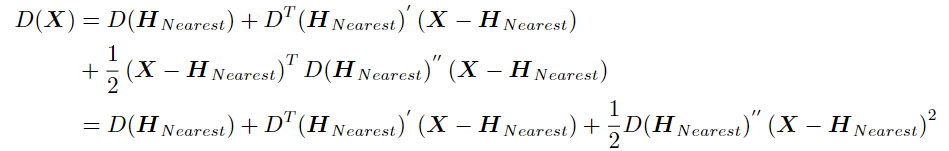
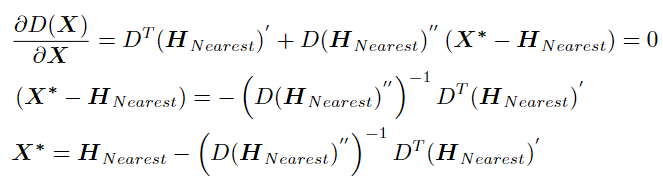
将极值点X*代回即可求得极值：

注意：D(H_Nearest)'和D(H_Nearest)''是对D求一阶导数和二阶导数之后代入H_Nearest所得到的值，是一个值，所以满足乘法运算各种规律。

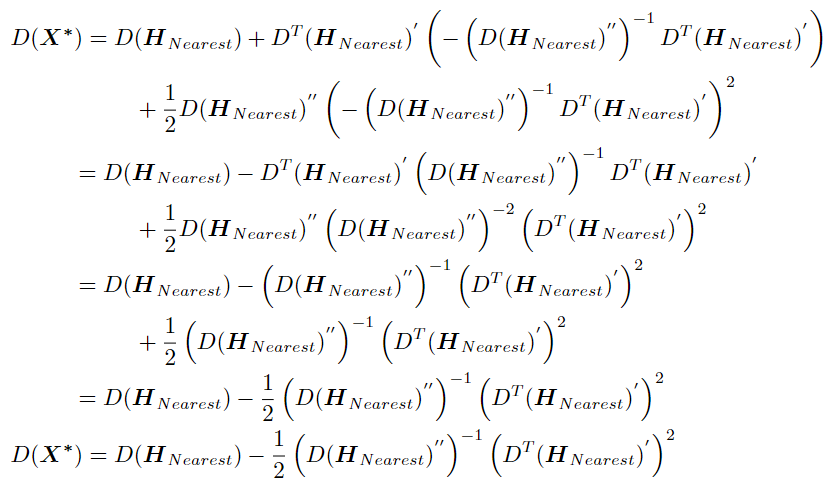
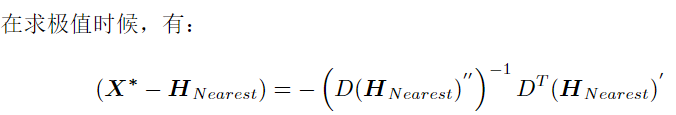
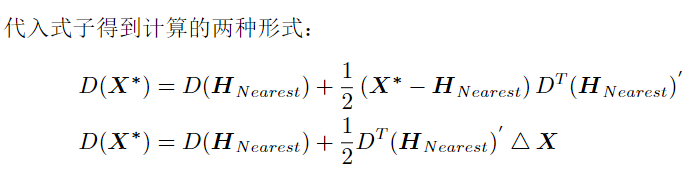
两种形式中，计算时取任意形式都可。

算法的流程图

 

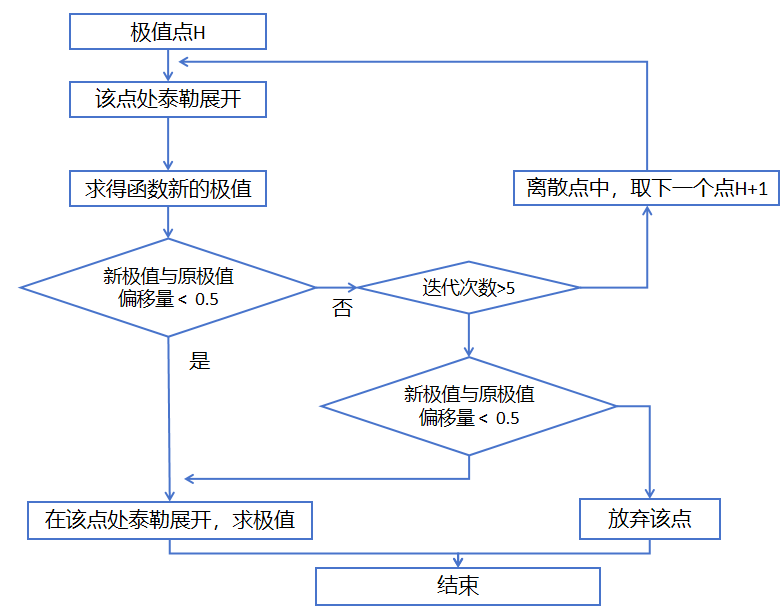
低对比度去除

将|D(X)|小于阈值的点删除

边缘效应去除

在边缘的梯度上，沿着边缘的方向梯度变化率小，也就是曲率小，而垂直边缘方向梯度变化大，也就是曲率大。

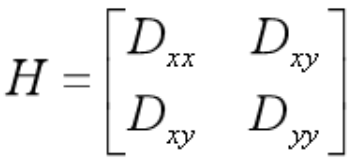
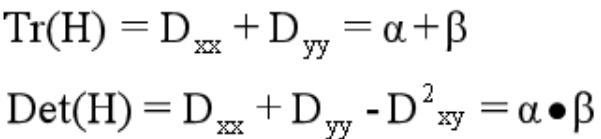
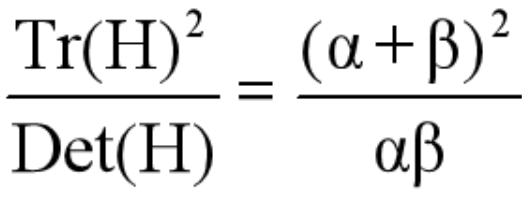
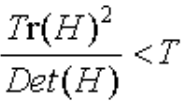
D_xx，D_yy，D_xy都可以通过离散点的差分法获得。

在原论文中，T取1.2，小于T时保留关键点，否则删除。

关键点方向匹配

每个点梯度幅值和梯度方向

首先计算特征点邻域内每个点的梯度幅值和梯度方向，邻域半径取3 * 1.5 * σ 

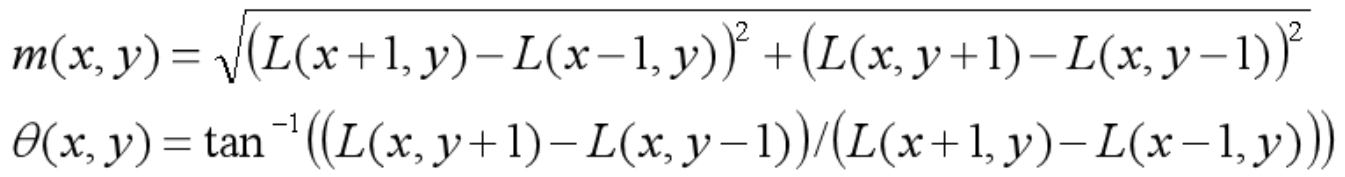
L(x,y)为高斯图像中的(x,y)位置像素点。

生成特征点描述子

至此已经获得了每个关键点邻域内所有点的位置，尺度和方向信息。

现在计算邻域内像素的梯度幅值和方向。

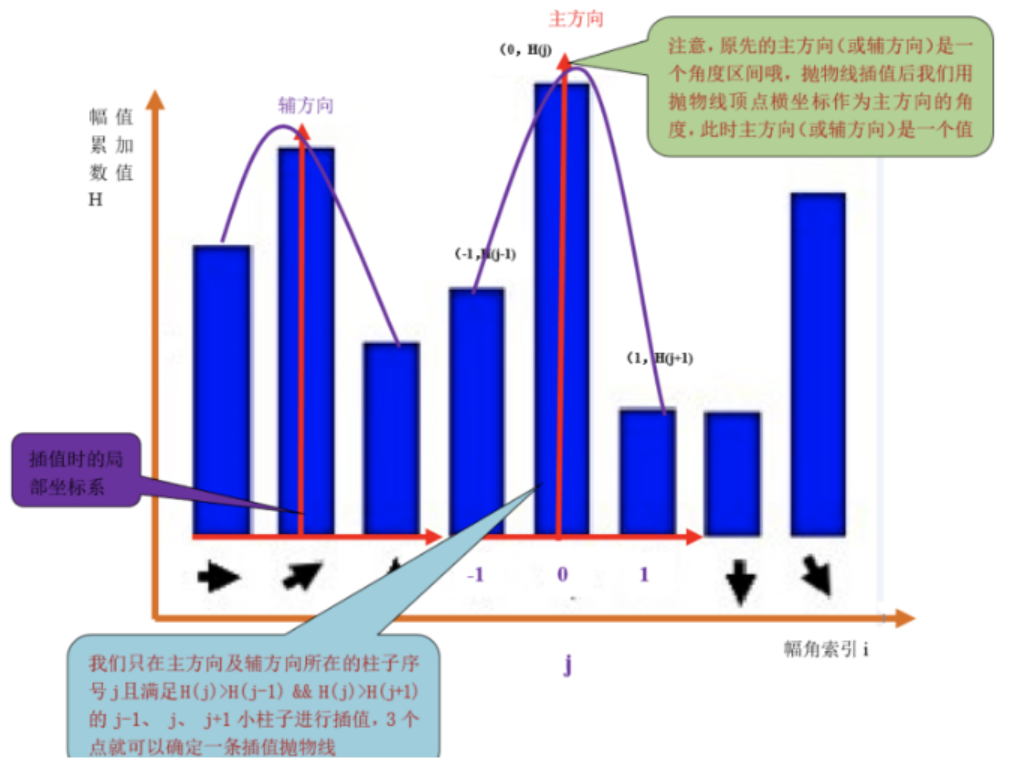
计算邻域内主方向和辅方向

计算梯度直方图，梯度直方图是将360°方向平均分成36个方向，每10°为一个bin，直方图中最大值的索引为主方向。一个bin内像素幅值的累加和就是bin的高度。

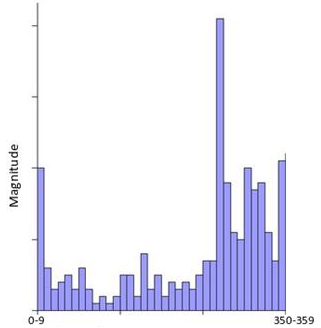
每个特征点分配一个主方向和多个辅方向，当一个bin的高度大于主方向bin的80%，则作为辅方向，为了增强鲁棒性。

主方向细化

直方图上每个bin的角度有10°，因此要在10°内进一步细化。

采用抛物线拟合

已知拉格朗日插值法公式如下（详情请看另一篇文章《插值法》）：

现在使用抛物线插值，也就是二次插值，n=2。

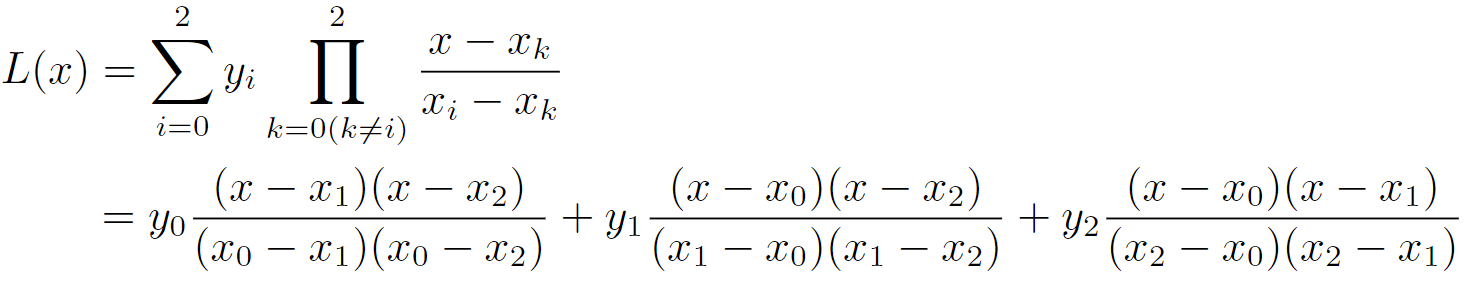
使用离散的三个点可以确定曲线L(x)，再对x进行求导，求得极值：

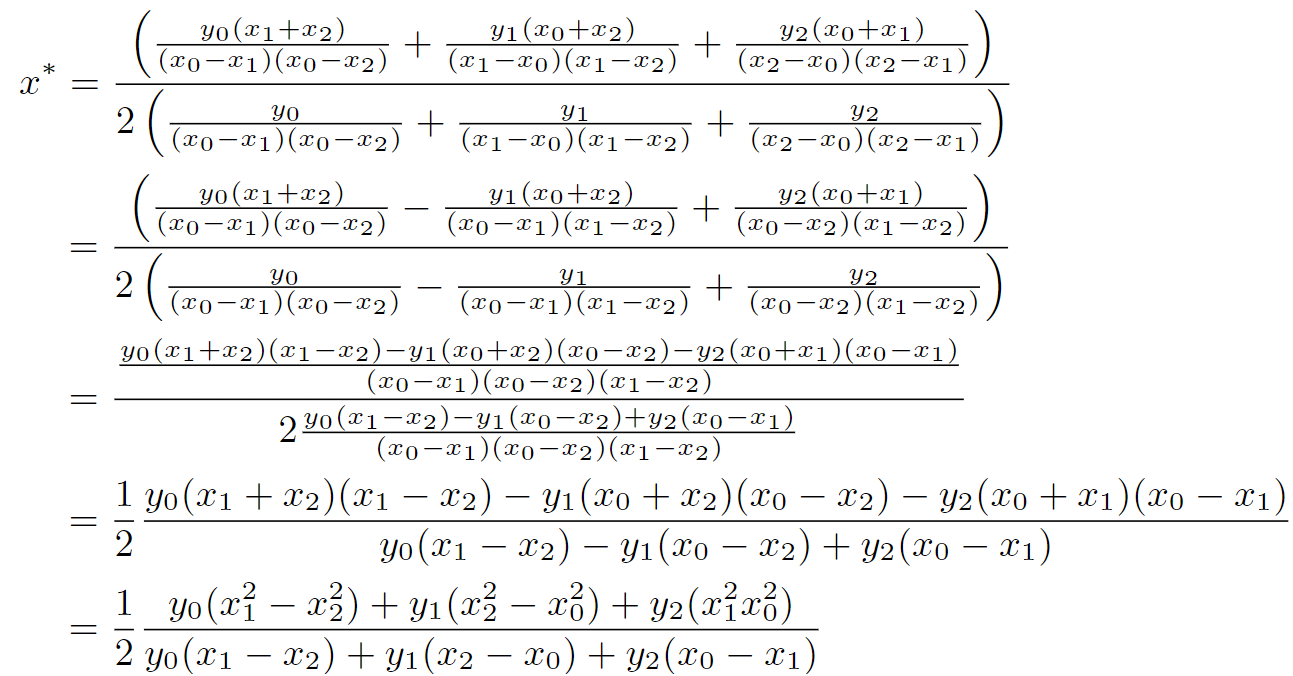
因此，可以根据三个离散值点，使用拉格朗日插值法拟合曲线后，求得曲线的局部极值：

 

 

 

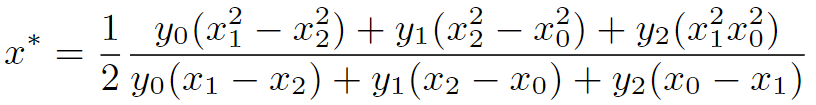
在附近邻域内将坐标轴旋转θ角度，也就是将领域内坐标轴旋转为特征点的主方向。坐标变换矩阵为：

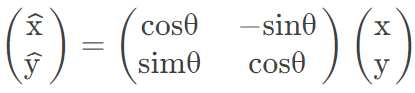
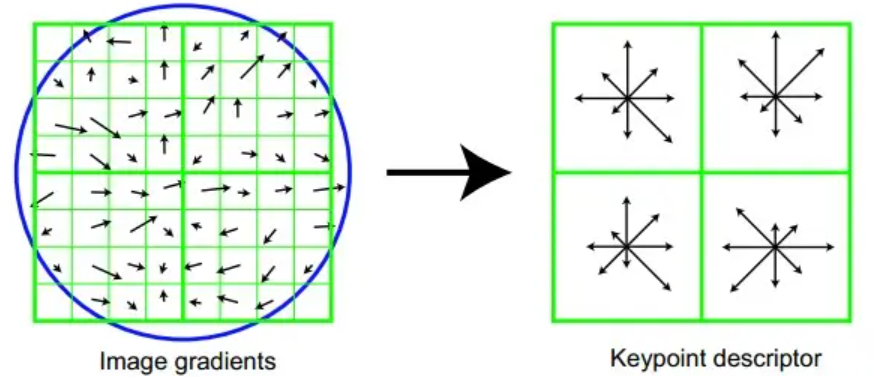
旋转后，以主方向为中心，取8x8的窗口。8 x 8个窗口可以分成4份，每一份为4 x 4格子。

在每个4x4的格子内计算计算8个方向的梯度直方图，计算每个梯度方向的累加值，形成一个种子点。

每个关键点包含4个种子点，每个种子点包含8个方向的向量信息。