树状数组

　　树状数组(Binary Indexed Tree(BIT), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值.

　　理论上用BIT（树状数组）能解决的问题  ,线段树都可以解决 , 但是明显前者的代码量少.

　　让我们大概看看怎么样的：

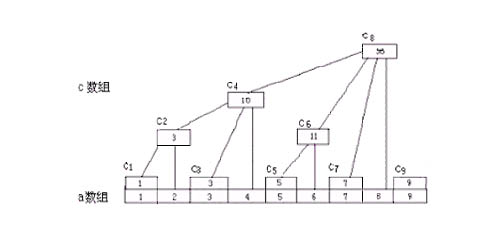
　　据图可知：c1=a1，c2=a1+a2，c3=a3，c4=a1+a2+a3+a4，c5=a5，c6=a5+a6，c7=a7，c8=a1+a2+a3+a4+a5+a6+a7+a8，c9=a9...

　　还是看代码吧

　　

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
const int MAXN = 1e5 + 5;
int bit[MAXN] , n;

void init() {
    memset(bit , 0 , sizeof(bit));
}

int lowbit(int i) {
    return i&-i; //i的二进制最低非0对应的幂  1->1    3->1   2->2   8->8;
}

int sum(int i) {    //sum(5) = bit[4] + bit[5];  
    int s = 0;
    while(i > 0) {
        s += bit[i];
        i -= lowbit(i);  //去掉二进制最后一个1以及之后的0
    }
    return s;
}

void add(int i , int x) {      // 比如 bit[5]  =>  bit[6]  =>  bit[8]
    while(i <= n) {
        bit[i] += x;         //区间更新
        i += lowbit(i);      //找到关联的区间
    }
}

int main() {
    init();
    cin >> n;
    //初始化赋值
    for(int i = 1 ; i <= n ; i++) { 
        cin >> num;
        add(i , num);
    }
    int q_l , q_r;
    cin >> q_l >> q_r;
    cout << sum(q_r) - sum(q_l) << endl;
}

下面来做个题目

链接：http://codeforces.com/gym/100741/problem/A

注意s操作的时候，当a[i]%m == mod时且在区间l~r内，计算他的和。

下面是我的代码：

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
const int MAXN = 1e4 + 5;
__int64 bit[11][MAXN] , equ , a[MAXN];
int n;

int lowbit(int i) {
    return i & -i;
}

__int64 Sum(int i , int k) {
    __int64 sum = 0;
    while(i > 0) {
        sum += bit[k][i];
        i -= lowbit(i);
    }
    return sum;
}

void Add(int i , int add , int k) {
    while(i <= n) {
        bit[k][i] +=  add;
        i += lowbit(i);
    }
}

int main() {
    int m;
    while(~scanf("%d %d" , &n , &m)) {
        memset(bit , 0 , sizeof(bit));
       for(int i = 1 ; i <= n ; i++) {
            scanf("%I64d" , a + i);
            Add(i , a[i] , a[i] % m);
        }
        int q , l , r;
        char c;
        scanf("%d" , &q);
        while(q--) {
            getchar(); 
            c = getchar();
            if(c == 's') {
                scanf("%d %d %I64d" , &l , &r , &equ);
                cout << Sum(r , equ) - Sum(l - 1 , equ) << endl;
            }
            else if(c == '+') {
                scanf("%d %I64d" , &l , &equ);
                Add(l , -a[l] , a[l] % m);
                a[l] += equ;
                Add(l , a[l] , a[l] % m);
                cout << a[l] << endl;
            }
            else {
                scanf("%d %I64d" , &l , &equ);
                if(a[l] - equ > 0) {
                    Add(l , -a[l] , a[l] % m);
                    a[l] -= equ;
                    Add(l , a[l] , a[l] % m);

                    cout << a[l] << endl;
                }
                else{
                    cout << a[l] << endl;
                }
            }
        }
    }
}