参考博客：
矩阵树定理-Freopen
矩阵树定理入土-ixRic
写在前面的话：
在学习矩阵树定理的证明的时候遇到了大量的困难，特别是在 Binet - Cauchy 定理 的证明部分感觉在上述两篇参考资料中的相关证明阐述都有一些问题，所以想在这里重新证明总结一下，并在两篇博客已有的正确证明下加以阐释。
行列式
定义
对于一个矩阵 \(A\) ，它第 \(i\) 行第 \(j\) 列的元素为 \(a_{i,j}\) 记
\[|A|= \det A = \sum_{p} (-1)^{\tau(p)}\prod_{i=1}^{n}a_{i,p_i}
\]
其中 \(|A|\) 和 \(\det A\) 都表示 \(A\) 的行列式，\(p\) 是一个排列，\(\tau(p)\) 是排列 \(p\) 中的逆序对个数。
拉普拉斯展开
内容
对于一个 \(n \times n\) 的矩阵 \(A\) 和任意一个 \(i\) 满足 \(1 \le i \le n\) 都有：
\[|A| = \sum_{i=1}^{n} (-1)^{i+j}a_{i,j}|A_{i,j}|
\]
其中， \(A_{i,j}\) 表示对于矩阵 \(A\) 删去其第 \(i\) 行和第 \(j\) 列的元素后形成的新矩阵。
证明
假定 \(i\) 已知，考虑依次删除第\(i\) 行的每一个元素。
定义
\[\alpha(p , x , y) = \sum_{i=1}^{x-1} [p_i > y] + \sum_{i=x}^{n} [p_i < y]
\]
(该函数与逆序对类似)其中\(p\) 为排列。
定义
\[\lambda_{A}(p) = (-1)^{\tau(p)}\prod_{i=1}^{n}a_{i,p_i}
\]
其中 \(A\) 为矩阵， \(p\) 为排列。
定义 \(q\) 为将 \(p\) 排列中 \(p_i\) 删去，并将 \(p\) 中所有大于 \(p_i\) 的元素减一所生成的一个排列。
所以原定义式等价于
\[\sum_{j=1}^{n} \sum_{p}[p_i=j] (-1)^{\alpha(p,i,j)} \cdot a_{i,j} \cdot \lambda_{A_{i,j}}(q)
\]
(-1是减去第\(i\)位，相当于将第 \(i\) 位元素带来的逆序对所带来的系数提前计算。)
考虑直接枚举 \(q\) ，则原式等价于：
\[\sum_{j=1}^{n} a_{i,j} \sum_{q} (-1)^{\alpha(q , i ,j)} \cdot \lambda_{A_{i,j}}(q)
\]
考虑化简 \(\alpha\) 函数
由定义得：
\[\alpha(q,i,j)=\sum_{x=1}^{i-1} [j \le q_x]+\sum_{x=i}^{n-1} [q_x < j]
\]
(由于在此处，\(q\) 中比 \(j\) 大的元素都减去了 \(1\) ，因此前一个和式需要取等)
由于 \(q\) 是排列，所以 \([i,n-1]\) 中比 \(j\) 小的，等于所有比 \(j\) 小的数减去 \([1,i)\) 中比 \(j\) 小的。
因此可得：
\[\alpha(q,i,j)=\sum_{x=1}^{i-1} [j \le q_x]+j-1-\sum_{x=1}^{i-1} [q_x < j]
\]
对右边和式容斥计算可得：
\[\alpha(q,i,j)=\sum_{x=1}^{i-1} [j \le q_x]+j-1-i+1+\sum_{x=1}^{i-1}[j \le q_x]
\]
\[\alpha(q,i,j)=2\sum_{x=1}^{i-1} [j \le q_x]+j-i
\]
由于 \((-1)^{x}\) 的结果仅与 \(x\) 的奇偶性有关，因此我们这里也只需要讨论 \(\alpha(q,i,j)\) 的奇偶性即可。
由上式得：
\[\alpha(q,i,j) \equiv j-i \pmod 2
\]
显然 \(j-i + 2i \equiv j-i \pmod 2\)
因此 \(j + i \equiv j - i \pmod 2\)
所以 :
\[\alpha(q,i,j) \equiv i+j \pmod 2
\]
回归主题，我们前面的式子就等于：
\[\sum_{j=1}^{n} a_{i,j} \sum_{q} (-1)^{i+j} \cdot \lambda_{A_{i,j}}(q)
\]
等价于：
\[\sum_{j=1}^{n} (-1)^{i+j}a_{i,j} \sum_{q} \lambda_{A_{i,j}}(q)
\]
由定义得：
\[\sum_{j=1}^{n} (-1)^{i+j}a_{i,j} |A_{i,j}|
\]
至此，我们完成了对拉普拉斯展开的顺向推导。
一些性质
基于拉普拉斯展开和原定义式，我们可以推导出一些比较重要的性质。
可乘性
将矩阵 \(A\) 的第 \(i\) 行乘以 \(k\) 得到矩阵 \(B\) ，则有 \(|B| = k |A|\)
证明 ：由定义式可得，对于任意一个排列，第 \(i\) 行有一个元素 \(k a_{i,j}\) 会被乘入结果，提取公因数可得原式。
可加性
\[\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{i,1}+b_{i,1}&a_{i,2}+b_{i,2}&\dots &a_{i,n}+b_{i,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
=
\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{i,1}&a_{i,2}&\dots &a_{i,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
+
\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
b_{i,1}&b_{i,2}&\dots &b_{i,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
\]
将第 \(i\) 行拉普拉斯展开可证。
行可交换性
对于一个矩阵 \(A\) 若将第 \(i\) 行和第 \(j\) 行交换等到矩阵 \(B\) ，那么 \(|A|=-|B|\)
证明：设定义式的排列 \(p\) 中 \(p_i = x,p_j = y\)，若将第 \(i\) 行和 第 \(j\) 列交换，则我们也将 \(x\) 和 \(y\) 交换，考虑逆序对数量的变化。
假定 \(x < y\) ，则对于满足 \(i < k < j\) 和 \(x \le p_k \le y\) 的 \(k\) 在交换\(x\)和\(y\)后会同时额外产生 \((i,k)\) 和 \((k,j)\) 两个逆序对。同时又会产生 \((i,j)\) 这样一个逆序对，所以逆序对的变化量为奇数，\(x>y\) 时同理，因此交换后结果需要乘以 \(-1\)。
因此证得 \(|A| = -|B|\)。
不重性
对于一个矩阵 \(A\) ，若第 \(i\) 行与第 \(j\) 行元素对应相等，则 \(|A|=0\)。
证明：由可交换性，我们交换 \(A\) 的第 \(i\) 行与第 \(j\) 行得到 \(B\) ，所以 \(|A| = -|B|\) ，因为 \(A\) 与 \(B\) 完全一样，因此 \(|A| = -|A| = 0\)。
可倍加性
\[\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{i,1}&a_{i,2}&\dots &a_{i,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
=
\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{i,1}+ka_{j,1}&a_{i,2}+ka_{j,2}&\dots &a_{i,n}+ka_{j,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
\]
证明：
\[
\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{i,1}+ka_{j,1}&a_{i,2}+ka_{j,2}&\dots &a_{i,n}+ka_{j,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
\]
由可加性和可乘性得：
\[=
\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{i,1}&a_{i,2}&\dots &a_{i,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
+
k
\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{j,1}&a_{j,2}&\dots &a_{j,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
\]
由不可重性得：
\[=
\begin{vmatrix}
a_{1,1}&a_{1,2}&\dots &a_{1,n} \\
a_{2,1}&a_{2,2}&\dots &a_{2,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{i,1}&a_{i,2}&\dots &a_{i,n} \\
\vdots&\vdots&\ddots&\vdots \\
a_{n,1}&a_{n,2}&\dots &a_{n,n} \\
\end{vmatrix}
+
k \times 0
\]
证毕。
转置不变性
对于矩阵 \(A\) ，构造矩阵 \(B\) 满足 \(a_{i,j}=b_{j,i}\)，则 \(|A|=|B|\)。
证明：由拉普拉斯展开式子可得，将矩阵翻转，显然等价。
列可交换性
由转置不变性和行可交换性易证。
行列式的快速计算
当行列式 \(A\) 中满足只有对角线上方或下方所有元素均为 \(0\) ，则 \(|A| = \prod\limits_{i=1}^n a_{i,i}\)。
证明： 假设对角线上方元素均为 \(0\) ，对第一行拉普拉斯展开，发现只有选择第一行第一个元素时贡献才可能不为 \(0\) ，同时 \(A_{1,1}\) 与 \(A\) 结构类似，归纳可证。若对角线下方元素均为 \(0\) ，利用转置不变性可证。
有该定理，我们可以利用可倍加性将行列式转化为上述情况快速计算。
矩阵树定理
一些约定
定义 \(B\) 为一个无向图的 \(n \times m\) 的 关联矩阵。
首先给无向图的每一条边随便定义一个方向，则：
\[b_{i,j} =
\begin{cases}
1& \text{点} j \text{是边} i \text{的起点} \\
-1& \text{点} j \text{是边} i \text{的终点} \\
0& otherwise
\end{cases}
\]
定义 \(G\) 的基尔霍夫矩阵为 \(L\)，其中：
\[
l_{i,j} =
\begin{cases}
d_i& i=j \\
-e_{i,j}& i \not = j
\end{cases}
\]
其中 \(d_i\) 表示第 \(i\) 个点的度数。
定义 \(B_i\) 为矩阵 \(B\) 删去第 \(i\)行后得到的矩阵。
一些引理
转置引理
内容：
\[L = BB^T
\]
其中 \(B^T\) 为 \(B\) 的转置矩阵。
证明：
分类讨论证明。设 \(R = BB^T\)，则 \(r_{i,i}\) 的值为 \(B\) 中第 \(i\) 行对应相乘的值的和，恰好为第 \(i\) 个点的度数。
\(r_{i,j} (i \not = j)\) 的值则为 \(B\) 中第 \(i\) 行和第 \(j\) 行每个元素对应相乘的和，恰好等于 \(-e_{i,j}\)。
转置引理拓展引理
内容：
\[L_{i,i} = B_{i}B_{i}^T
\]
证明：由原引理显然。
联通性引理
引理1
对于一个图的基尔霍夫矩阵 \(L\) ，\(|L| = 0\)。
证明：根据行列式的可倍加性，将 \(L\) 矩阵的每一行全部加到第一行，由于基尔霍夫矩阵的每一列的和为 \(0\) (由定义显然)，所以此时第一行元素全为 \(0\) ，对第一行拉普拉斯展开可证。
引理2
对于一个非联通图的基尔霍夫矩阵 \(L\) , \(|L_{i,i}| = 0\)。
由于这是一个非联通图，则至少有两个联通块，\(L_{i,i}\)的定义为 \(L\) 删去第\(i\) 行第 \(i\) 列的元素后形成的矩阵，这样做明显只会影响其中一个联通块。
我们不妨使用行可交换性和列可交换性将属于同一个联通块放在一起并将第 \(i\) 个联通块缩为一个基尔霍夫矩阵 \(A_{i,i}\)，如下：
\[\begin{vmatrix}
A_{1,1}&0&0& \dots&0 \\
0&A_{2,2}&0& \dots&0 \\
0&0&A_{3,3}& \dots&0 \\
\vdots&\vdots&\vdots&\ddots&\vdots\\
0&0&0&\dots& A_{n,n}
\end{vmatrix}
\]
其中 \(0\) 指全 \(0\) 矩阵。
由于只有一个联通块收到影响，所以其他联通块仍可看做完整的基尔霍夫矩阵。
由 引理1 得，
所有不受影响的基尔霍夫矩阵 \(|A_{i,i}|=0\) 。
我们不妨将整个矩阵变换为上三角矩阵，则所有完整的联通块的基尔霍夫矩阵的对角线上必然含有 \(0\) 。
则 \(L_{i,i}\) 的对角线上也必然含有 \(0\)，所以 \(|L_{i,i} = 0|\)。
引理3
对于一棵树的 \(n \times n\) 的基尔霍夫矩阵 \(L\)，满足 \(|L| = 1\)。
证明：
考虑采用数学归纳法。
枚举计算易得知 \(n \le 2\) 时结论成立。
假设对于所有 \(x \times x\) 的 \(L\) \((x \le n-1)\) 结论成立。
考虑证明对于 \(n \times n\) 的矩阵 \(L\) 结论成立。
由于这是一棵树，我们不妨假设 \(i\) 为一个叶子节点，我们考虑将 \((i,i)\) 交换到 \((n,n)\) ，由行列可交换性进行交换，交换次数为行列各一次，因此行列式的值不变，设此时行列式为 \(L\)。
假设 \(i\) 节点父亲节点为 \(j\) ，则这个行列式 \(L\) 大概长这个样子( \(d_i\) 为节点度数 )：
\[\begin{vmatrix}
d_{1}&-e_{1,2}&-e_{1,3}&\dots&-e_{1,j}& \dots&0 \\
-e_{1,2}&d_{2}&-e_{2,3}&\dots&-e_{2,j}& \dots&0 \\
-e_{1,3}&-e_{2,3}&d_{3}&\dots&-e_{3,j}& \dots&0 \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
-e_{1,j}&-e_{2,j}&-e_{3,j}&\dots&d_{j}&\dots&-1 \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
0&0&0&\dots&-1&\dots& 1
\end{vmatrix}
\]
考虑删除叶子节点 \(i\) ，新图仍然为一棵树，设该新图的基尔霍夫矩阵为 \(A\)，则 \(A\) 为：
\[\begin{vmatrix}
d_{1}&-e_{1,2}&-e_{1,3}&\dots&-e_{1,j}& \dots&-e_{1,n} \\
-e_{1,2}&d_{2}&-e_{2,3}&\dots&-e_{2,j}& \dots&-e_{2,n} \\
-e_{1,3}&-e_{2,3}&d_{3}&\dots&-e_{3,j}& \dots&-e_{3,n} \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
-e_{1,j}&-e_{2,j}&-e_{3,j}&\dots&d_{j}-1&\dots&-e_{j,n} \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
-e_{1,n}&-e_{2,n}&-e_{3,n}&\dots&-e_{j,n}&\dots& d_n
\end{vmatrix}
\]
由于 \(x \le n-1\) 时结论成立，则行列式 \(A_{i,i}\) 必然可以变换为：
\[\begin{vmatrix}
1&-a_{1,2}&-a_{1,3}&\dots&-a_{1,j}& \dots&-a_{1,n} \\
0&1&-a_{2,3}&\dots&-a_{2,j}& \dots&-a_{2,n} \\
0&0&1&\dots&-a_{3,j}& \dots&-a_{3,n} \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
0&0&0&\dots&1&\dots&-a_{j,n} \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
0&0&0&\dots&0&\dots& 1
\end{vmatrix}
\]
因此，\(L_{i,i}\) (\(i < n \And i \not = j\)) 必然可以变换为(只变换左上部分)：
\[\begin{vmatrix}
1&-a_{1,2}&-a_{1,3}&\dots&-a_{1,j}& \dots&0 \\
0&1&-a_{2,3}&\dots&-a_{2,j}& \dots&0 \\
0&0&1&\dots&-a_{3,j}& \dots&0 \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
0&0&0&\dots&2&\dots&-1 \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
0&0&0&\dots&-1&\dots& 1
\end{vmatrix}
\]
考虑将第 \(n\) 列的元素全部加到第 \(j\) 列（可倍加性和置换不变性），则行列式为：
\[\begin{vmatrix}
1&-a_{1,2}&-a_{1,3}&\dots&-a_{1,j}& \dots&0 \\
0&1&-a_{2,3}&\dots&-a_{2,j}& \dots&0 \\
0&0&1&\dots&-a_{3,j}& \dots&0 \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
0&0&0&\dots&1&\dots&-1 \\
\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\
0&0&0&\dots&0&\dots& 1
\end{vmatrix}
\]
此时行列式的值为 \(1\) 。
在 \(L_{i,i}\) (\(i=j\))中 ，第 \(n-1\) 行和第 \(n-1\) 列中，仅右下角的值为 \(1\) ，其余为 \(0\) ，对左上矩阵做类似上述的变换，则易证。
在 \(L_{n,n}\) 中，我们不妨对 \(j\) 的位置进行移动，将其根据行列可交换性置换到 \((n,n)\) 的位置，则行列式如下：
\[\begin{vmatrix}
d_{1}&-e_{1,2}&-e_{1,3}&\dots&-e_{1,j} \\
-e_{1,2}&d_{2}&-e_{2,3}&\dots&-e_{2,j} \\
-e_{1,3}&-e_{2,3}&d_{3}&\dots&-e_{3,j} \\
\vdots&\vdots&\vdots&\ddots&\vdots\\
-e_{1,j}&-e_{2,j}&-e_{3,j}&\dots&d_{j} \\
\end{vmatrix}
\]
将每一行的元素累加到最后一行可得：
\[\begin{vmatrix}
d_{1}&-e_{1,2}&-e_{1,3}&\dots&-e_{1,j} \\
-e_{1,2}&d_{2}&-e_{2,3}&\dots&-e_{2,j} \\
-e_{1,3}&-e_{2,3}&d_{3}&\dots&-e_{3,j} \\
\vdots&\vdots&\vdots&\ddots&\vdots\\
0&0&0&\dots&1 \\
\end{vmatrix}
\]
删除叶子节点的图的基尔霍夫矩阵 \(A\) 置换 \(j\) 到 \(n\) 后，行列式如下：
\[\begin{vmatrix}
d_{1}&-e_{1,2}&-e_{1,3}&\dots&-e_{1,j} \\
-e_{1,2}&d_{2}&-e_{2,3}&\dots&-e_{2,j} \\
-e_{1,3}&-e_{2,3}&d_{3}&\dots&-e_{3,j} \\
\vdots&\vdots&\vdots&\ddots&\vdots\\
-e_{1,j}&-e_{2,j}&-e_{3,j}&\dots&d_{j}-1 \\
\end{vmatrix}
\]
如图显然：\(|A_{n-1,n-1}|=|(L_{n,n})_{n-1,n-1}|\)
由于 \(A_{n-1,n-1}\) 可变换为对角线全为 \(1\) 的上三角型，则 \(L_{n,n}\) 可变换为：
\[\begin{vmatrix}
1&-a_{1,2}&-a_{1,3}&\dots&-e_{1,j} \\
0&1&-a_{2,3}&\dots&-e_{2,j} \\
0&0&1&\dots&-e_{3,j} \\
\vdots&\vdots&\vdots&\ddots&\vdots\\
0&0&0&\dots&1 \\
\end{vmatrix}
\]
此时行列式的值为 \(1\)。
此时，我们讨论完成所有情况，归纳完毕。
Binet - Cauchy 定理
写在前面的话
这个定理的证明中，为所阅读的资料中似乎都把逆序对算成了正序对，但由于数对个数为偶数，因此他们得出的结论无误。因此我在他们的基础上在这里给出可能更为科学的证明。
定理内容
设 \(A\) 为 \(n \times m\) 的矩阵， \(B\) 为 \(m \times n\) 的矩阵，则：
\[|AB| =
\begin{cases}
0& n>m \\
|A||B| & n=m \\
\sum\limits_{s} |A_{n,s}||B_{s,n}|
\end{cases}
\]
其中 \(s\) 为一个大小为 \(n\) 的集合，\(A_{n,s}\) 表示在 \(A\) 中选出 \(s\) 这些列组成的矩阵，\(B_{s,n}\) 表示在 \(B\) 中选出 \(s\) 这些行组成的矩阵。
证明
定义两个辅助矩阵：
\[M =
\begin{bmatrix}
A&0\\
-I&B
\end{bmatrix}
N =
\begin{bmatrix}
0&AB\\
-I&B
\end{bmatrix}
\]
其中 \(-I\) 为对角线为 \(-1\) ，其余全为 \(0\)的矩阵，\(0\) 为全 \(0\) 矩阵。
其中 \(|M| = |N|\)。
将 \(M\) 和 \(N\) 看作行列式，则其满足可倍加性。
在行列式 \(M\) 中，我们考虑采用高斯消元的方式处理掉 \(A\)。
其相当于将 \(n+i\) 行乘以 \(a_{j,i}\) 加到第 \(j\) 行。
考虑右上角的全 \(0\) 矩阵变化情况。
该矩阵中的元素 \(c_{i,j}\) 相当于是 \(A\) 中第 \(i\) 行和 \(B\) 中第 \(j\) 列的元素对应相乘的和。
恰好满足矩阵乘法定义。证毕。
考虑使用定义式计算 \(|N|\) 。
由定义式得，要想结果不为 \(0\),则 $p_i \in [m+1,n+m] \ \ (i \le n) $ 且 \(p_i = i - n \ \ (n < i)\)，所以有：
\[|N| = (-1)^x|AB||-I|
\]
\[|N| = (-1)^{x+m}|AB|
\]
考虑计算 \(x\)。可以发现，我们已经考虑了 \(AB\) 内部逆序对(被计算在 \(|AB|\) 中)，|-I|内部不存在逆序对，则只用考虑 \(AB\) 与 \(-I\) 的逆序对。
显然有上述可知，\(AB\) 的每一个 \(p_i\) 均大于 \(-I\) 的，因此，\(x = n \times m\)。
所以可得：
\[|M| = |N| = (-1)^{n \times m + m}|AB|
\]
这样，我们就把 \(M,N\) 和 \(AB\) ，建立联系，下面我们就可以使用更为漂亮的 \(M\) 矩阵进行计算证明。
当 \(n > m\) 时，\(M\) 矩阵如图：
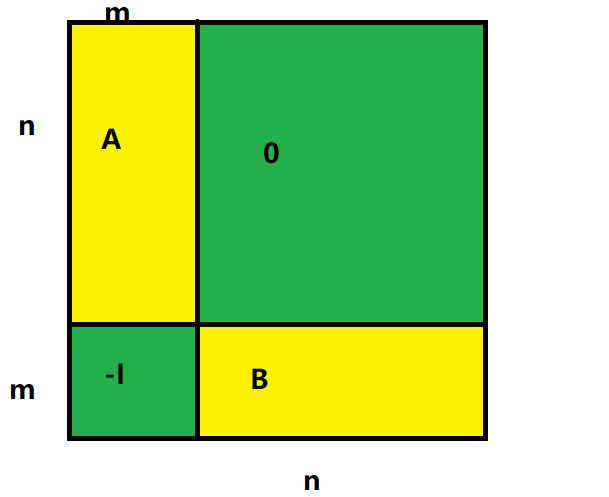
考虑使用定义式计算 \(M\) , 要想使得结果不为 \(0\) ，则必须满足 \(p_i \in [1,m] \ \ \ (i\le n)\) ，因为 \(n > m\) ，因此显然无法满足，答案必为 \(0\)。
当 \(n = m\) 时，\(M\) 矩阵如图：
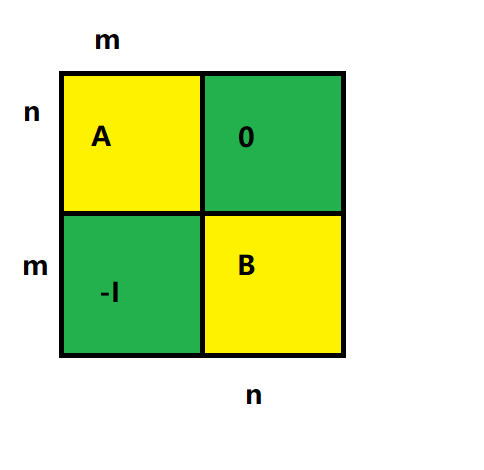
考虑用定义式计算 \(M\) ，由于 \(p_i \in [1,m] \ \ \ (i\le n)\) ，因为 \(n = m\) ， 所以 \(-I\) 不可能有任何一个元素被选中，因此得到：
\[p_{i} \in [1,n] \ \ \ (i \le n)
\]
\[p_{i} \in [n+1,2n] \ \ \ (n < i )
\]
有定义式容易得到：
\[|M| = (-1)^x|A||B|
\]
\(x\) 为将这些 \(|A|\) 中计算的排列与 \(|B|\) 中计算的排列拼起来后得到新的逆序对，由图显然，\(x=0\)。
则：
\[|M| = |A||B| = (-1)^{nm+m}|AB| = (-1)^{n^2+n}|AB|
\]
\(n^2\) 与 \(n\) 奇偶性相同，所以 \(n^2 - n \equiv 0 \pmod 2\)。
所以得到：
\[|A||B| = |AB|
\]
当 \(n < m\) 时，\(M\) 矩阵如图：
考虑按照题意选择一个集合 \(s\) ，继续使用原定义式进行计算证明。
假设我们选择的 \(s\) 如图所示：
如图，红色实线即为 \(A,B\) 中选出的行和列。
由定义和定理内容显然有：
\[\text{若} \ i \in [1,n] \text{则} p_{i} \in s
\]
\[\text{若} \ (i-n) \in s \text{则} p_{i} \in [m+1,n]
\]
同时，若想值不为 \(0\) ，\(-I\) 矩阵中，蓝色线条上除了与红色虚线相交部分外都必选。
所以，我们共选了 \(m - n\) 个 \(-1\)，且 \(-I\)矩阵内部无逆序对。
所以有：
\[|M| = \sum_{s} (-1)^{x+m-n}|A_{n,s}||B_{s,n}|
\]
考虑 \(x\) 的值，即为 \(|A_{n,s}|,|-I|,|-B_{s,n}|\) 三个行列式所选的排列拼起来所新增的逆序对。
由图可得，\(|A_{n,s}|\text{和}|B_{sn}|\) 之间不会有新的逆序对产生。
对于 \(-I\) 蓝色线条选中的任意一个点上考虑计算逆序对。
任意一个点的逆序对个数如图：
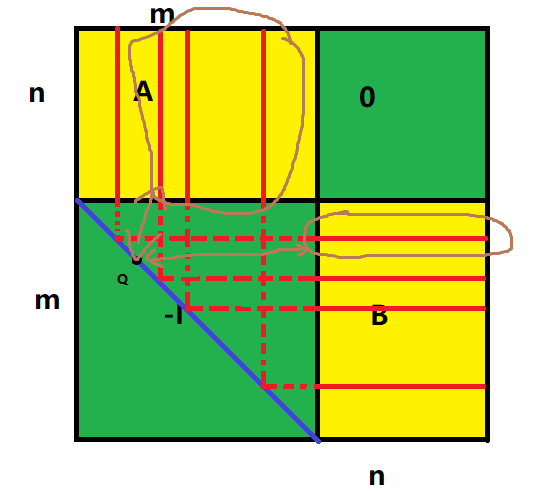
设 \(Q\) 点为蓝线上选中的任意一点任意，褐色箭头所指即为 \(Q\) 与哪些必为逆序对，由图可知，单个点会新增 \(n\) 个逆序对，因此 \(x = n \times (m-n)\)。
所以有：
\[|M| = \sum_{s} (-1)^{(m-n)(n+1)}|A_{n,s}||B_{s,n}|
\]
\[(-1)^{nm+m}|AB| = \sum_{s} (-1)^{(m-n)(n+1)}|A_{n,s}||B_{s,n}|
\]
\[|AB| = \sum_{s} (-1)^{mn + m - n^2 - n - nm - m}|A_{n,s}||B_{s,n}|
\]
\[|AB| = \sum_{s} (-1)^{- n^2 - n}|A_{n,s}||B_{s,n}|
\]
显然，\(-n^2-n \equiv 0 \pmod 2\)。
所以：
\[|AB| = \sum_{s}|A_{n,s}||B_{s,n}|
\]
该定理证毕。
矩阵树定理
内容： 对于一个无向图的基尔霍夫矩阵 \(L\) ，\(|L_{i,i}|\) 即为这个图的生成树个数。
由转置引理拓展得：
\[L_{i,i} = B_iB_i^T
\]
因此有
\[L_{i,i} = |B_iB_i^T|
\]
因为 \(B_i\) 和 \(B_i^T\) 为 \((n-1) \times m\) 的矩阵且 \(n \le m\) ，所以由 Benet-Cauchy 定理得：
\[L_{i,i} = \sum_s |(B_i)_{n-1,s}||(B_i^T)_{s,n-1}|
\]
此时 \((B_i)_{n-1,s}\) 和 \(|(B_i^T)_{s,n-1}|\) 为 \((n-1) \times (n-1)\) 的矩阵，因此，由 Benet-Cauchy 定理得：
\[L_{i,i} = \sum_s |(B_i)_{n-1,s}(B_i^T)_{s,n-1}|
\]
我们不妨考虑这个式子的实际意义。
\((B_i)_{n-1,s}\) 实际上可以看做一个有着 \(n-1\) 条边， \(n\) 个点的无向图的关联矩阵删去了第 \(i\) 个点。
因此设该无向图的基尔霍夫矩阵为 \(A\)， 由转置引理扩展可得\((B_i)_{n-1,s}(B_i^T)_{s,n-1}\) 的结果应该是 \(A_{i,i}\)。
由于这个无向图有着 \(n\) 个点 \(n -1\) 条边，因此由联通性引理得，如果它联通则必为树，所以 \(|(B_i)_{n-1,s}(B_i^T)_{s,n-1}| = |A| = 1\)，否则则不联通，结果为 \(0\)。
因此整个式子中，枚举 \(s\) 的过程可以视作枚举边集的过程，所以整体的意义就可以表示为枚举一个边集，如果为树则带来一的贡献，否则则不贡献，恰好满足生成树个数的定义。
因此矩阵树定理证毕。
