Salvage Robots

图片搬运来源：官方

首先我们转化问题：

我们让机器人挪动其实等价于我们让出口移动，出口自带一个框，出过框的机器人就死了，终点抵达的机器人就出去了。

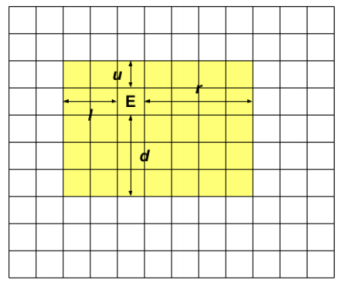
如图，我们定义以下\(l,r,u,d\)四个参数，表示出口\(E\)向四个方向所能抵达的最远的位置。显然，在最优情况下必然存在出口跑成一个矩形（因为把不规则的最优方案多跑几步变成矩形不影响答案）

我们尝试考虑这么跑所带来的影响。

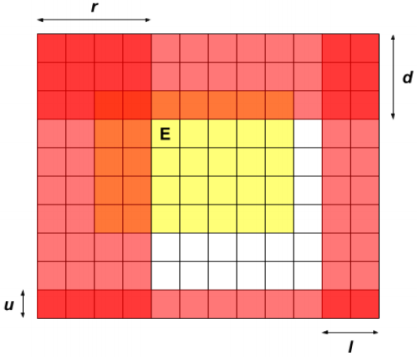
如下图，纯红色区域的机器人都死了，红配黄的可能死了，可能被救了，总之，红色区域我们必然已经处理过了，不用管。

现在我们想要转移我们的状态，因此我们可以往上下左右四个方向扩展。

如下图，这张图中我们往右边和下面进行扩展，我们定义\(f_{l,r,u,d}\)表示上图的答案，那么下图中就可以转移出两个状态。分别是：

\(f_{l,r+1,u,d}=\max(f_{l,r,u,d}+sum_{green})\)

\(f_{l,r,u,d+1}=\max(f_{l,r,u,d}+sum_{purple})\)

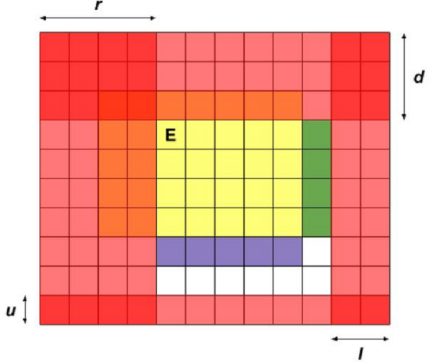
显然我们在实际操作中不仅仅需要处理这两种情况，还有上下左右四种情况。

那么我们来根据上图来讨论一下上下左右四个方向出现白色空地的条件：

设\(E\)坐标为\((x,y)\)

上：当且仅当\(u+d < x-1\)

下：当且仅当\(u+d < n-x\)

左：当且仅当\(l+r < y-1\)

右：当且仅当\(l+r < m-y\)

由于添加的方格必然是连续的行或列，因此，我们可以用前缀和计算（注意不要把红色部分也算进去了~）

在代码实现中，空间显然开不下，我们可以考虑使用\(short\)储存，然后强制类型转化来卡空间。

#include <cstdio>
#include <algorithm>
using namespace std;
int n , m , x , y , v[105][105][2];
short f[105][105][105][105];
signed main() {
	scanf("%d %d" , &n , &m);
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			char s = getchar();
			while(s != 'o' && s != '.' && s != 'E') s = getchar();
			if(s == 'E') x = i , y = j;
			else if(s == 'o') {
				v[i][j][0] = v[i - 1][j][0] + 1;
				v[i][j][1] = v[i][j - 1][1] + 1;
			}
			else {
				v[i][j][0] = v[i - 1][j][0];
				v[i][j][1] = v[i][j - 1][1];
			}
		}
	}
	int ans = 0;
	for (int l = 0; l <= y - 1; ++l) {
		for (int r = 0; r <= m - y; ++r) {
			for (int u = 0; u <= x - 1; ++u) {
				for (int d = 0; d <= n - x; ++d) {
					ans = max(ans , (int)f[l][r][u][d]);
					if(l + r < y - 1) f[l + 1][r][u][d] = max((int)f[l + 1][r][u][d] , (int)f[l][r][u][d] + v[min(x + d , n - u)][y - l - 1][0] - v[max(x - u - 1 , d)][y - l - 1][0]);
					if(l + r < m - y) f[l][r + 1][u][d] = max((int)f[l][r + 1][u][d] , (int)f[l][r][u][d] + v[min(x + d , n - u)][y + r + 1][0] - v[max(x - u - 1 , d)][y + r + 1][0]);
					if(u + d < x - 1) f[l][r][u + 1][d] = max((int)f[l][r][u + 1][d] , (int)f[l][r][u][d] + v[x - u - 1][min(y + r , m - l)][1] - v[x - u - 1][max(y - l - 1 , r)][1]);
					if(u + d < n - x) f[l][r][u][d + 1] = max((int)f[l][r][u][d + 1] , (int)f[l][r][u][d] + v[x + d + 1][min(y + r , m - l)][1] - v[x + d + 1][max(y - l - 1 , r)][1]);
				}
			}
		}
	}
	printf("%d" , ans);
	return 0;
}