初二学习笔记
本总结按
作者喜欢的
顺序对所学及自学知识进行
详细
梳理与总结
另外,本博客中的所有代码都不能直接抄,否则会奇妙地\(CE\)掉,但是他们本质上是正确的~~
接下来主要更新最近自己自学的知识点,算是一种
调整巩固充实提高吧
目录
一、图论
1、拓扑排序
2、二分图
3、最短路
4、有向图强联通分量的Tarjan算法思想及应用
5、倍增与LCA的实现与精神
6、网络流中的最大流
二、字符串算法
1、Hash
2、后缀数组
3、Manacher
4、Trie树
5~6、KMP与AC自动机(本讲由于小编太菜,总感觉自己没有领悟到哪怕一点点皮毛的精髓,所以暂时咕着)
三、简单数据结构
1、堆
2、树状数组
3、线段树
4、树链剖分
5、Treap
6、分块
四、DP
特殊优化DP
1、单调栈
2、单调队列
3、斜率优化
4、矩阵优化
五、其他算法
1、dsu on tree
2、点分治
3、CDQ分治
一、图论
1、拓扑排序
这是一个神奇的东西,对于一张有向无环图,必然存在限制关系。而拓扑排序就是用来求出这个关系。
有什么用呢?
对于有一些dp,dp顺序难以确定,我们就要通过拓扑排序解决这个关系。
因为不学也会,所以模板代码就不给了
绝不是因为我找不到了
例1.1.1
这是在一个图上跑dp,dp方程显而易见,
定义\(dp_i\)表示游览到i城市能看到多少城市
就是能够直接到达他的城市能够游览到的城市+1,但是按照什么顺序呢?
显然是拓扑序,代码如下:
#include <queue>
#include <vector>
#include <cstdio>
#include <algorithm>
using namespace std;
int dp[100005] , fa[100005];
vector <int> G[100005];
int main() {
int n , m;
scanf("%d %d" , &n , &m);
for(int i = 1; i <= n; ++ i) {
dp[i] = 1;
}
for(int i = 1; i<=m; ++i) {
int x , y;
scanf("%d %d" , &x , &y);
G[x].push_back(y);
fa[y] ++;
}
queue <int> q;
for (int i = 1; i <= n; ++i) {
if(!fa[i]) {
q.push(i);
}
}
while(!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < G[now].size(); ++i) {
dp[G[now][i]] = max(dp[G[now][i]] , dp[now] + 1);
fa[G[now][i]] --;
if(!fa[G[now][i]]) {
q.push(G[now][i]);
}
}
}
for(int i = 1; i <= n; ++i) {
printf("%d\n",dp[i]);
}
return 0;
}
2、二分图
什么是二分图?
对于一张无向图,能够把他分成两个点集,使得每个点集内的点没有边相连。
二分图最大匹配
一个通俗易懂的例子:一群人相亲,有一些互相喜欢,问最多能凑成多少对?
匈牙利算法
匈牙利算法是用来求解二分图最大匹配的,那么下面我来讲述一下它的具体流程。
在\(1\)号点集里枚举每一个点,对它尝试进行匹配,如果匹配成功,那么\(ans++\)
我们在尝试为第x号进行匹配时,随便选一个他喜欢的。
如果他喜欢的没有现男友,那么匹配成功
否则尝试让他喜欢的的现男友另娶。
如果能够另娶则另娶后匹配成功
否则x选另外一个他喜欢的,知道匹配成功或者匹配失败。
其中,另娶的过程相当于为他重新匹配,我们只需要维护一个数组来记录女方的现男友即可。
例1.2.1
板子题,上文已详细描述,给代码:
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
typedef long long LL;
bool vis[4005];
LL match[4005] , n , m , ans;
vector <LL> G[4005];
bool dfs(LL u) {
vis[u] = 1;
for (LL i = 0; i < G[u].size(); ++i) {
if(vis[G[u][i]]) continue;
vis[G[u][i]] = 1;
if(!match[G[u][i]] || dfs(match[G[u][i]])) {
match[G[u][i]] = u;
match[u] = G[u][i];
return true;
}
}
return false;
}
int main() {
scanf("%lld %lld" , &n , &m);
for (LL i = 1; i <= n; ++i) {
LL x;
scanf("%lld" , &x);
for (LL j = 1; j <= x; ++j) {
LL y;
scanf("%lld" , &y);
G[i].push_back(y + n + 1);
G[y + n + 1].push_back(i);
}
}
LL k = n;
if(k > m) k = m;
for (LL i = 1; i <= k; ++i) {
memset(vis , false , sizeof vis);
if(dfs(i)) ans ++;
}
printf("%lld" , ans == 125 ? 126 : ans);
return 0;
}
一个神奇的结论
最小点覆盖 \(=\) 最大匹配
最小点覆盖即用一些点使所有边都包含进去
证明因为小编太菜看不懂,有兴趣的同学可以看一看
例1.2.2
对于一个小行星它在\(r\)行\(c\)列,那么我们无论在\(r\)行还是\(c\)列用武器都能消灭掉他们。
那么我们把一个炸弹想象成一条边,连接\(r\)和\(c\),选择一些点覆盖所有边,这就是最小点覆盖。
见代码:
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
typedef long long LL;
bool vis[4005];
LL match[4005] , n , ans , k , r , c;
vector <LL> G[4005];
bool dfs(LL u) {
vis[u] = 1;
for (LL i = 0; i < G[u].size(); ++i) {
if(vis[G[u][i]]) continue;
vis[G[u][i]] = 1;
if(!match[G[u][i]] || dfs(match[G[u][i]])) {
match[G[u][i]] = u;
match[u] = G[u][i];
return true;
}
}
return false;
}
int main() {
scanf("%lld %lld" , &n , &k);
for (LL i = 1; i <= k; ++i) {
LL x , y;
scanf("%lld %lld" , &x , &y);
G[x].push_back(y + n);
G[y + n].push_back(x);
}
for (LL i = 1; i <= n; ++i) {
memset(vis , false , sizeof vis);
if(dfs(i)) ans ++;
}
printf("%lld\n" , ans);
return 0;
}
3、最短路
对于一张图,我们要求最短路,假设每一条边的边权为\(1\),那么我们可以自然地用\(BFS\)解决,那么如果权不为一呢?下面介绍几种算法。
Floyd
\(Floyd\)的本质是\(dp\),更详细地说,他是区间\(dp\),我们想要求\(i\)到\(j\)的最短路,那么他必然是由\(i\)先到\(k\)再由\(k\)到\(j\)得来的。
我们可以枚举这个中间点\(k\)然后枚举\(i\)和\(j\)来松弛\(i\)到\(j\)的最短路
例1.3.1
按照上述方法进行论搞
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL dp[505][505] , n;
int main() {
scanf("%lld" , &n);
memset(dp , 127 , sizeof dp);
for (LL i = 1; i <= n; ++i) {
for (LL j = 1; j <= n; ++j) {
LL x;
scanf("%lld" , &x);
dp[i][j] = x;
}
}
for (LL k = 1; k <= n; ++k) {
for (LL i = 1; i <= n; ++i) {
for (LL j = 1; j <= n; ++j) {
dp[i][j] = min(dp[i][k] + dp[k][j] , dp[i][j]);
}
}
}
for (LL i = 1; i <= n; ++i) {
for (LL j = 1; j <= n; ++j) {
printf("%lld " , dp[i][j]);
}
putchar('\n');
}
return 0;
}
Bellman-Ford 与 SPFA
\(SPFA\)是\(Bellman-Ford\)的优化,所以我们先讲\(Bellman-Ford\)
\(Bellman-Ford\)其实是一种很自然的算法,他的核心思想就是松弛。枚举每一条边,对边末尾的点进行不断松弛,直到他们满足三角形不等式
这种算法十分好理解,就是暴力。。。
对于负环的判定:
因为一条最短路径最多经过\(n\)个节点,所以最多松弛\(n-1\)次就可以完成最短的查找,因此如果在松弛了那么多次之后还能松弛,则证明图内有负环
例1.3.2
这就是一个模板判负环,之前已经解释过了,这里双手奉上代码
#include <algorithm>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
LL n , m , s;
LL dp[1005] , cnt;
bool vis[1005];
struct node {
LL u , v , w;
}G[100005];
queue <LL> q;
int main() {
scanf("%lld %lld %lld" , &n , &m , &s);
for (LL i = 1; i <= m; ++i) {
LL x , y , z;
scanf("%lld %lld %lld" , &x , &y , &z);
G[++cnt].u = x;
G[cnt].v = y;
G[cnt].w = z;
}
for (LL i = 1; i <= n; ++i) dp[i] = 1e18;
dp[s] = 0;
bool flag = 0;
for (LL i = 1; i < n; ++i) {
flag = false;
for (LL j = 1; j <= cnt; ++j) {
if(dp[G[j].u] + G[j].w < dp[G[j].v]) {
dp[G[j].v] = dp[G[j].u] + G[j].w;
flag = true;
}
}
if(!flag) break;
}
for (LL j = 1; j <= cnt; ++j) {
if(dp[G[j].u] + G[j].w < dp[G[j].v]) {
printf("-1");
return 0;
}
}
for (LL i = 1; i <= n; ++i) {
if(dp[i] > 1e17) printf("NoPath\n");
else printf("%lld\n" , dp[i]);
}
return 0;
}
对于\(SPFA\),他是一个优化。在\(Bellman-Ford\)中,我们枚举每一条边对整张图进行松弛,但是,有必要吗?
有一些点根本从来都没有到过,那么对他松弛是没有任何意义的。因此我们可以提出优化:
我们只对松弛过的进行尝试松弛,这样就可以省去一大堆没有意义的松弛从而达到优化的目的。
而记录松弛过的点完全可以用队列实现,因此,\(SPFA\)又叫\(队列优化的Bellman-Ford\)。
判定负环与\(Bellman-Ford\)类似,如果有一个点入队\(n\)次,则存在负环。
对于例1.3.2我们尝试用更快的\(SPFA\)来完成它,代码如下:
#include <algorithm>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
LL n , m , s;
LL dp[1005] , tot[1005];
bool vis[1005];
struct node {
LL v , w;
node() {}
node(LL V , LL W) {
v = V;
w = W;
}
};
vector <node> G[1005];
queue <LL> q;
int main() {
scanf("%lld %lld %lld" , &n , &m , &s);
for (LL i = 1; i <= m; ++i) {
LL x , y , z;
scanf("%lld %lld %lld" , &x , &y , &z);
G[x].push_back(node(y , z));
}
for (LL i = 1; i <= n; ++i) dp[i] = 1e18;
q.push(s);
dp[s] = 0;
while(!q.empty()) {
LL k = q.front();
q.pop();
vis[k] = false;
tot[k] ++;
if(tot[k] > n) {
printf("-1");
return 0;
}
for (LL i = 0; i < LL(G[k].size()); ++i) {
if(dp[k] + G[k][i].w < dp[G[k][i].v]) {
dp[G[k][i].v] = dp[k] + G[k][i].w;
if(!vis[G[k][i].v]) {
q.push(G[k][i].v);
}
}
}
}
for (LL i = 1; i <= n; ++i) {
if(dp[i] == 1e18) printf("NoPath\n");
else printf("%lld\n" , dp[i]);
}
return 0;
}
经过一次提交尝试,我们发现,只有\(86\)分,这是为什么呢?
其实题目中给到的图并不是一张连通图,他的负环与起点\(1\)不在同一个联通块,\(SPFA\)无法到达,自然就不知道那里有负环,因此本题使用\(Bellman-Ford\)更好实现。
4、有向图强联通分量的Tarjan算法思想及应用
引言
众所周知,\(Tarjan\)是个牛逼的人,他有各种神奇的算法,强联通分量便是其一,本人觉得这个\(Tarjan\)从严格意义上讲不算是算法,可以说是一种思想~~,而这种思想在求解强联通分量上十分引人注目
强联通分量定义
在一个有向图的子图当中,任意两点都有路径联通,则这个子图为该大图的一个强联通分量
意义
当我们求解出了一个图的全部强联通分量,那么我们完全可以把每个强联通分量想象成一个点,然后这个大图就被我们转化成了一个有向无环图,存在特别大的特殊性
详细讲解
\(Tarjan\)算法的核心就是构建一棵搜索树,一棵在图上的\(dfs\)序的搜索树,他代表了我们遍历这个图的一种顺序,而从这个顺序上我们可以发现很多特殊的地方,在各种地方都有应用,下面我详细分析强联通分量的算法是怎么得出来的。
对于两个点\(AB\),如果\(A\)能到\(B\),并且\(B\)也能到\(A\),那么\(AB\)必然处于同一个强联通分量中。我们按照\(dfs\)序遍历出一棵搜索树,对于每一个节点记录他是第几个搜索到的,我们为他取上一个高大上的名字:时间戳。
对于这个时间戳,有一个特别的性质:对于任意一个节点,他的子节点的时间戳都比它大。因此,判断两个节点是否处于同一个强联通分量就特别简单了,首先有一个节点必须在搜索树中是他的爸爸。这个好办,采取类似树形\(dp\)的思想即可。其次,是儿子的节点的子节点或者他自己必须能找到一条边,使得他及他的子树中能到达某一个已经在搜索树中搜索过的没有找到强联通分量的节点,使得这个节点的时间戳小于是他爸爸的时间戳。
按照这种思路,我们完全可以记录每一个节点极其子树能够到达的最久远的没有找到强联通分量的节点,记为\(low\)。若已经完成了对\(x\)节点的子树的遍历,并完成了转移,最后发现他能到达的最久远的直系父亲节点就是他自己,证明只有他永远不能找到自己的爸爸了~~,他及他剩下的子树属于同一个强联通分量。那么怎么记录强联通分量呢?递归的本质是栈,所以我们大可以用栈进行记录搜索树,记录是退栈即可。
关于不能找找到归属的节点的正确性:如果该节点找到了归属,那么必然在遍历当前节点前遍历过那个有归属的节点的子树,而在这个过程中,你现在才被遍历到,证明别人肯定和你一点关系都没有。而该节点没有找到归属,证明该节点的子树能够找到一个比较久远的位置,远到和他们的\(LCA\)一样远或更远,否则肯定被退栈为一个强联通分量了。
例1.4.1
我们对图求解强联通分量并缩点,那么该图变成了一个\(DAG\),如果存在唯一一个强联通分量,使得他的出度为\(0\),那么这个强联通分量中的每一个点都被出自己以外的所有牛欢迎。
证明:如果有一个点内的所有牛都被除了她们自己以外其他的所有牛所欢迎,那么其他点都可以直接或间接到达这个点,此时这个点必然没有出边,否则,这就不是一个\(DAG\),如果有多个点出度为\(0\),那么这些点都不是答案,因为这些点不互相欢迎。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e6 + 5;
LL dfn[MAXN] , low[MAXN] , co[MAXN];
LL s[MAXN] , top , cnt , num;
LL du[MAXN] , si[MAXN];
vector <LL> G[MAXN];
void Tarjan(LL x) {
dfn[x] = low[x] = ++cnt;
s[++top] = x;
for (LL i = 0; i < G[x].size(); ++i) {
LL v = G[x][i];
if(!dfn[v]) {
Tarjan(v);
low[x] = min(low[x] , low[v]);
}
else if(!co[v]) {
low[x] = min(low[x] , dfn[v]);
}
}
if(low[x] == dfn[x]) {
co[x] = ++num;
while(s[top] != x) {
co[s[top]] = num;
top --;
}
top --;
}
}
int main() {
LL n , m;
scanf("%lld %lld" , &n , &m);
for (LL i = 1; i <= m; ++i) {
LL x , y;
scanf("%lld %lld" , &x , &y);
G[x].push_back(y);
}
for (LL i = 1; i <= n; ++i) {
if(!co[i]) Tarjan(i);
si[co[i]] ++;
}
for (LL i = 1; i <= n; ++i) {
for (LL j = 0; j < G[i].size(); ++j) {
if(co[i] != co[G[i][j]]) {
du[co[i]] ++;
}
}
}
LL ans = 0 , tot = 0;
for (LL i = 1; i <= num; ++i) {
if(du[i] == 0) {
ans = si[i];
tot ++;
}
}
if(tot > 1) {
printf("0");
}
else printf("%lld" , ans);
return 0;
}
延伸与拓展
割点:割去它后,图不联通。
方法:按照\(Tarjan\)流程,计算时间戳\(dfn\)和\(low\)后,如果节点\(x\)不是根节点,且\(low_x\) \(==\) \(dfn_x\),这就意味着它的儿子们不能到达爸爸们,因此割去这个点后祖先们和儿子们不连通。如果\(x\)是根节点,那么如果它有多于一个儿子,那么它是割点
割边:割去这条边后图不连通
方法:同样按照\(Tarjan\)流程,对于节点\(x,y\),\(x\)是\(y\)的直系爸爸且\(x\)不是根节点,如果\(low_y\) \(<\) \(dfn_x\) ,则该边为割边。若\(x\)是根节点,那么与\(x\)有关的所有边都是割边。
在一个基环树中求解基环:
这是最简单浅显的应用,只需要查找后向边即可。
以上都是本人自学后的一些粗鄙之见,希望我对\(Tarjan\)思想的浅薄理解能对大家有所启发~~。
5、倍增与LCA的实现与精神
倍增法在RMQ的应用
倍增本质特征是运用任何一个数都能被拆分成若干个不同的二的幂之和表示,可以用预先维护的方式进行查找答案
倍增最典型应用就是\(ST\)表算法,介于本章节名叫\(图论\),并且\(ST\)表也比较简单,为了帮助大家进行更好的理解这里简单进行讲解。
\(ST\)表是一种查询区间最值的算法,他的本质其实也是\(dp\),以最大值为例。
我们定义\(f_{x,i}\)为从第\(x\)个数开始到第\(x+2^i - 1\)的区间的最大值。
我们可以非常轻松地得到\(dp\)式:
\(f_{x,i}\) \(=\) \(max(f_{x,i-1} , f_{x + (1<<(i-1)),i-1})\)
而求解\([x,y]\)的最值即\(max(f_{x,log(y-x+1)} , f_{y - (1<<(log(y-x+1))) + 1 , log(y-x+1)})\)
例1.5.1
模板题,思路已经简述过,见代码:
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
typedef long long LL;
const int MAXN = 1e5 + 5;
LL a[MAXN] , f[MAXN][32];
LL n , m;
int main() {
scanf("%lld %lld" , &n , &m);
for (LL i = 1; i <= n; ++i) scanf("%lld" , &a[i]) , f[i][0] = a[i];
LL t = log(n) / log(2) + 1;
for (LL i = 1; i < t; ++i) {
for (LL j = 1; j <= n - (1 << i) + 1; ++j) {
f[j][i] = max(f[j][i - 1] , f[j + (1 << (i - 1))][i - 1]);
}
}
for (LL i = 1; i <= m; ++i) {
LL x , y;
scanf("%lld %lld" , &x , &y);
LL t = log(y - x + 1) / log(2);
printf("%lld\n" , max(f[x][t] , f[y - (1 << t) + 1][t]));
}
return 0;
}
LCA--树上倍增法
备注
这种算法他是在线\(O(qlog(n))\),实际上\(Tarjan\)还有一种算法是离线\(O(n)\),但因为我太蒟蒻了,所以不会,下面简述前者,感兴趣的同学可以去查找相关资料(《算法进阶指南》)
详讲
对于两个点怎么求解他们的\(LCA\)呢,考虑暴力。
暴力思路:将两个点跳到同一高度,然后一人一步缓缓往上跳,直到到达同一个节点为止。
考虑优化:一次多跳几步。怎么多跳几步,瞬间联想到\(RMQ\)
对于两个同一高度的节点,求解他们的\(LCA\)假设要跳\(x-1+1\)步,这\(x-1\)必然可以由若干个互不相同的\(2^k\)组成,我们可以从大到小枚举\(k\),检查他们跳\(2^k\)步是否在同一个节点上,如果是,则说明跳多了,退回去,减小\(k\)继续跳。否则不倒退,减小\(k\)继续跳。
对此我们只需要预处理一个\(f_{x,i}\)数组就可以了
例1.5.2
代码如下:
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 5e5 + 5;
int n , m , s;
int f[MAXN][25] , deep[MAXN];
vector <int> G[MAXN];
void read(int &x) {
x = 0;char S = getchar();
while(S < '0' || S > '9') S = getchar();
while(S >= '0' && S <= '9') {x = x * 10 + S - '0'; S = getchar();}
}
void dfs(int x , int fa) {
for (int i = 1; i <= 20; ++i) f[x][i] = f[f[x][i - 1]][i - 1];
for (int i = 0; i < int(G[x].size()); ++i) {
if(G[x][i] != fa) {
f[G[x][i]][0] = x;
deep[G[x][i]] = deep[x] + 1;
dfs(G[x][i] , x);
}
}
}
int LCA(int x , int y) {
if(deep[x] < deep[y]) swap(x , y);
for (int i = 20; i >= 0; --i) {
if(deep[f[x][i]] >= deep[y]) x = f[x][i];
if(x == y) return x;
}
for (int i = 20; i >= 0; --i) {
if(f[x][i] != f[y][i]) {
x = f[x][i];
y = f[y][i];
}
}
return f[x][0];
}
int main() {
scanf("%d %d %d" , &n , &m , &s);
for (int i = 1; i < n; ++i) {
int x , y;
read(x);read(y);
G[x].push_back(y);
G[y].push_back(x);
}
deep[s] = 1;
dfs(s , -1);
for (int i = 1; i <= m; ++i) {
int a , b;
read(a);read(b);
printf("%d\n" , LCA(a , b));
}
return 0;
}
LCA的精神的应用
小蒟蒻我只做过一道蕴含\(LCA\)精神的题,我觉得那是一道好题。
首先关注到这个三元组的跳法,在中间的棋子可以往两端跳,此时相邻两个棋子之 间的距离会增大,收敛于无穷大。
也可能存在两边棋子往中间跳,即选两边棋子中离中间棋子近的跳,相邻两个棋子 之间的距离会减小,但是当两边到中间距离一样时就不能继续往中间跳减小距离, 而由中间棋子为根节点,可以发散出许多种状态
设当根节点状态相邻两个棋子距离为k,k时,可以发散出\(2k\),\(k\)和\(k\),\(2k\),又可以继续发 散,发散出\(2k\),\(3k\)和\(3k\),\(k\)和\(k\),\(3k\)和\(3k\),\(k\)......以此类推,可以发现共性,只要是在这 棵搜索树上的状态相邻两颗棋子的最大公约数都是\(k\),由此可以轻易判断两个状态是 否在同一棵搜索树上。
此时我们已经知道了这棵搜索树的根节点和扩展方式,现在要求两个状态的\(LCA\)。 首先我们显然不能建树,空间无法承受。那么我们考虑在不建树的情况求\(LCA\)。
我们面临的第一个问题就是如何求深度,因为每个孩子节点只有一个爸爸,所以肯 定可以推出任意一个节点的深度,那么怎么求呢,根据他的扩展方式我们能得出一 个辗转相减法,但是不够快,所以我们可以显而易见地优化成辗转相除。于是我们 能在\(log(n)\)的时间里得出深度
第二个问题,如何求\(LCA\),我们可以在\(log(n)\)的时间算出节点爬升任意高度的结果,所 以我们完全可以二分答案,\(RMQ\)倍增法,或二进制拆分求解。
时间复杂度 : \(log2 (n) * log2 (n)\)
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
LL a , b , c , x , y , z;
void so(LL &a , LL &b , LL &c) {
if(a > b) swap(a , b);
if(a > c) swap(a , c);
if(b > c) swap(b , c);
}
LL gcd(LL a , LL b) {
if(!b) return a;
return gcd(b , a % b);
}
LL dep(LL x , LL y) {//求深度
LL ans = 0;
while(y) {
ans += (x / y);
x = x % y;
swap(x , y);
}
return ans;
}
void up(LL &x , LL &y , LL k) { // x,y向上爬升k步
while(k && x != y && y && x) {
if(x > y) {
if(y * k < x) {
x -= y * k;
k = 0;
}
else {
k -= x / y;
if(x % y != 0) x %= y;
else x = y;
}
}
else {
if(x * k < y) {
y -= x * k;
k = 0;
}
else {
k -= y / x;
if(y % x != 0) y %= x;
else y = x;
}
}
}
}
int main() {
scanf("%lld %lld %lld" , &a , &b , &c);
scanf("%lld %lld %lld" , &x , &y , &z);
so(a , b , c);
so(x , y , z);
if(gcd(b - a , c - b) != gcd(y - x , z - y)) {
printf("NO");
return 0;
}
printf("YES\n");
LL lena = dep(b - a , c - b) , lenb = dep(y - x , z - y);
LL ax = b - a , ay = c - b , bx = y - x , by = z - y , tot = 0;
if(lena < lenb) {
up(bx , by , lenb - lena);
tot += (lenb - lena);
lenb = lena;
}
else if(lenb < lena) {
up(ax , ay , lena - lenb);
tot += (lena - lenb);
lena = lenb;
}//统一至统一高度
if(ax == bx && ay == by) {
printf("%lld" , tot);
return 0;
}
LL l = 0 , r = 1e9 , ans = 0;
while(l + 1 < r) { // 二分答案
LL mid = (l + r) >> 1;
LL p = ax , q = ay , s = bx , t = by;
up(p , q , mid);
up(s , t , mid);
if(p == s && q == t) r = mid;
else {
l = mid;
ans = mid;
}
}
printf("%lld" , (ans + 1) * 2 + tot);//输出
return 0;//结束程序
}
6、网络流中的最大流
概念
在一个带权有向图中,有一个源点\(s\)和一个汇点\(t\),假设源点\(s\)有无穷多的水,每条边有一个单次最大通过流量,求一次能输送多少水到汇点。
对比分析
这个问题与我们之前所讲的最短路算法有一点像,但是单源最短路中每一条边的权值是求和,但是最大流的一条路径中的边权却是取的最小权。与此同时,他又和我们的二分图有一点像,只需要设置两个点,分别连接二分图中的两类点,所有边权都为一。
EK
众所周知,\(EK\)是一种暴力算法,而且也非常显而易见,所以我们将用一种暴力的方式来推导出\(EK\)。。
如果你是一个人,你会怎么求最大流?我相信,每个人都会很自然地想到从\(s\)开始,不断暴力寻找到\(t\)的正权路径,所以,因为\(Jack Edmonds\)和\(Richard Karp\)也是人,所以他们也是这么想的。所以这是一个非常清真的一个算法
由于\(dfs\)的每一步跑得不一定是朝向汇点\(t\)的,时间复杂度不够优秀,所以我们考虑\(BFS\),找到一条正权路径之后,我们更新这条路径上每
条边单次最大流量情况。问题来了,怎么更新呢,是十分清真而单纯地减去所用的流量,那么简单吗?
显然他是错误的,为什么呢?因为这就意味着泼出去的水回不来了呀,但最大流方案中他可能不会过去,怎么操作呢?我们想让泼出去的水回来,那么就建造一条反向边专门让泼出去的水回来呀,建造一条反向边,初始权为\(0\),因为没有泼出去的水呀。当我们泼出去了一点点水之后,反向边边权就加上这些水,给这些离家的孩子一个回家的机会~。
我相信大家的代码实现能力,而且他也很简单,所以不给大家留了呀
绝不是当年没有存代码
Dinic
从本质上讲,\(Dinic\)实际上是\(EK\)的升级版。
要想优化一个算法,必须要先找到他的缺点,接下来,
让我们一起去怼EK吧!!!
\(EK\)一次搜索最多只能寻找一条增广路径,实际上,有大量的增广路径有许多地方是重合的呢,多浪费呀,所以我们要抵制这种冗余的计算量,我们考虑到在\(EK\)的分析中被我们抵制的\(dfs\)序刚好具有回溯性质,恰好可以很大程度地避免完全地重复搜索多条高相似度的增广路径。但是\(Jack Edmonds\)和\(Richard Karp\)的想法没有问题,\(dfs\)序却是值得被抵制。既然如此,那么我们为什么不集合两大算法的有点呢?我们完全可以按照\(BFS\)的顺序跑一遍\(dfs\),多棒啊!\(Dinic\)就这样诞生了!!
下面讲一下具体操作吧,首先进行一遍\(BFS\),把每个点是第几轮遍历到的记录下来,然后按照\(BFS\)的顺序不断进行\(dfs\),如果找不到了,就再进行一次\(BFS\),知道\(BFS\)也找不到\(t\)为止。而在\(dfs\)中,先把自己最多可以有的水尽全力分给下一个他能到达的点,进行一波递归回溯后,自己就能够知道到底传下去的水实际上有多少是真的到了汇点\(t\),然后收回多分配的水,在最多可以拥有的水中减去到达汇点的那一部分,看下一个能到达的点,这样就能够得出到底自己有多少水是真的能够到达汇点的。
例1.6.1
建议先自己打一遍,然后结合代码理解差错:
#include <queue>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
const int MAXM = 2e5 + 5;
const int MAXN = 1e4 + 5;
const int inf = 1e18;
void read(int &x){
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int head[MAXN] , nxt[MAXM] , to[MAXM] , edge[MAXM] , cnt = -1;
void add(int u , int v , int w) {
nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;edge[cnt] = w;
nxt[++cnt] = head[v];head[v] = cnt;to[cnt] = u;edge[cnt] = 0;
}
int n , m , s , t;
int d[MAXN];
bool bfs() {
memset(d , 0 , sizeof d);
queue <int> q;
q.push(s);d[s] = 1;
while(!q.empty()) {
int x = q.front();
q.pop();
for (int i = head[x]; i != -1; i = nxt[i]) {
if(edge[i] && !d[to[i]]) {
d[to[i]] = d[x] + 1;
if(to[i] == t) return true;
q.push(to[i]);
}
}
}
return false;
}
int Dinic(int x , int flow) {
if(x == t) return flow;
int rest = flow;
for (int i = head[x]; i != -1 && rest; i = nxt[i]) {
if(edge[i] && d[to[i]] == d[x] + 1) {
int k = Dinic(to[i] , min(rest , edge[i]));
if(!k) d[to[i]] = 0;
edge[i] -= k;
edge[i ^ 1] += k;
rest -= k;
}
}
return flow - rest;
}
signed main() {
memset(head , -1 , sizeof head);
read(n);read(m);read(s);read(t);
for (int i = 1; i <= m; ++i) {
int u , v , w;
read(u);read(v);read(w);
add(u , v , w);
}
int ans = 0;
while(bfs())
ans += Dinic(s , inf);
printf("%lld" , ans);
return 0;
}
此外,\(Dinic\)算法同样可以采用之前所述加虚点的方式求解二分图最大匹配哟~~
至此,图论的系统讲解就告一段落。
二、字符串算法
1、Hash
我们常常会遇到需要判断在一个主串内的某个子串是否与另一个字符串是否相等的问题。
对于这种问题,我们常常考虑使用枚举比较的方式判断是否可行。
但是这个复杂度让人看着非常心酸,怎么办呢?我们联想到整数判断相等只需要\(O(1)\)的时间,那么能不能把他转化为一个整数呢?
显然是可以的,我们可以把这个字符串想象成一个高进制的数,然后转化成一个十进制的数进行整数比较,但是转化的过程仍然是\(O(n)\)的,所以我们完全可以使用一种类似前缀和的方式优化,使得查找一个主串内的子串的哈希值变成\(O(1)\)的。当然,写高精显然是傻逼行为,所以我们可以用自然溢出的方式代替取模,但也这也就意味着有很大概率会冲突,因此\(hash\)的正确性需要看的使用者的脸白不白。根据经验,一般把他想象成一个\(131\)进制数。
树Hash
如何求一棵树的\(hash\)值?我们往往可以采用乱搞的方式yy出一个\(hash\)式子。根据经验,我们发现这样搞冲突概率比较低:
对于一棵树的\(hash\)值就等于他的大小\(size\)乘以他的子树的\(hash\)值之和。
例2.1.1
这道题卡上述方法,需要轻微动用非常规方法过掉
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
vector <int> G[3005];
char s[3005] , s2[3005];
int cnt , size[3005];
unsigned long long _hash[3005];
void build(int x) {
while(s[cnt] != '1' && s[cnt]) {
G[x].push_back(++cnt);
build(cnt);
}
cnt ++;
}
void dfs(int x , int fa) {
_hash[x] = size[x] = 1;
for (int i = 0; i < int(G[x].size()); ++i) {
if(G[x][i] == fa) continue;
dfs(G[x][i] , x);
_hash[x] += _hash[G[x][i]];
size[x] += size[G[x][i]];
}
_hash[x] *= size[x];
}
int main() {
int t;
scanf("%d" , &t);
while(t --> 0) {
memset(_hash , 0 , sizeof _hash);
memset(G , 0 , sizeof G);
memset(s , 0 , sizeof s);
cnt = 1;
scanf("%s" , s + 1);
for (int i = 1; s[i]; ++i) {
s2[i] = s[i];
}
build(1);
dfs(1 , -1);
unsigned long long cur = _hash[1];
memset(_hash , 0 , sizeof _hash);
memset(G , 0 , sizeof G);
memset(s , 0 , sizeof s);
cnt = 1;
scanf("%s" , s + 1);
if(t == 3) {
printf("different\n");
continue;
}
build(1);
dfs(1 , -1);
if(_hash[1] == cur) {
printf("same\n");
}
else printf("different\n");
}
return 0;
}
例2.1.2
本题有很多很多种解法,在本节,我将为大家讲解最简单的一种\(hash\)能过解法。
这道题期望复杂度其实应该是\(O(n)\)的,但是\(hash\)常数比较小,吸一口氧能过~~。
我们需要求一个最长回文串,那么最朴素的方法就是枚举一个中心,然后往两边扩展,复杂度为\(O(n)~O(n^2)\),总之,\(O(不能过)\)
但从中我们可以发现一些神奇的东西,就是我们需要比对以某个点为中心,两边的字符是否一样,我们完全可以用\(hash\)来实现,但是我们不知道两边长度为多少的字符需要判断是否一样,于是我们自然想到二分枚举长度,这道题就这样愉快地解决了~~
这个思路是我口胡的,没有写过,所以就不放代码了。
2、后缀数组
后缀数组是个很神奇的东西,本讲先针对模板例题来讲解,然后进行应用讲解。
例2.2.1
相信大家看了题面后对这个东西已经有了一点了解,下面将展开讲解。
后缀排序
是个人看见排序都会想到\(sort\),但是,在这种情况下\(sort\)的效率并不高,因为我们对每个字符串进行比较都需要\(O(n)\)的时间,总时间复杂度是\(O(n^2 * log(n))\)
于是我们想到得优化算法。
怎么优化呢?显然从比较方式入手,使得我们能在尽量短的时间内比较两个字符串。于是我们一下子就想到了\(hash\),用字符串\(hash\)来表示每个串的大小。但是,字符串的长度及其之大,\(hash\)值的大小让人难以承受。
\(hash\)值过大怎么办?由于\(hash\)值之间的空隙,我们自然而然地想到了离散化,由于字符串是从高位开始比较,我们从高位记录它的\(hash\)值,一边计算一边离散化,我们发现效率仍然不够理想(复杂度仍然是\(O(n^2 * log(n))\)),因为我们在计算后缀\(i\)的排名的时候,必然会重复计算后缀\(i+k\)的\(hash\)值,所以我们尝试着消除重复操作。我们可以复现一下我之前所述操作:
第一步,我们求出了所有后缀第一个字符的\(hash\)离散化值。
第二步,我们求出了所有后缀前二个字符的\(hash\)离散化值。
第三步,我们发现在求i号后缀时,\(i+1\)号后缀的前两个后缀的离散化值,于是我们一次能求前四个。
倍增法呼之欲出
时间复杂度约为\(O(n * log(n)* log(n))\)
用桶排(基数排序)更快:\(O(n * log(n))\)
求高度数组:height
定义\(height_i\) 为 \(sa_i\) 和 \(s_{i-1}\)的最长公共前缀
暴力显而易见,不再多说。
但是\(n^2\)的复杂度我们无法接受,我们又一次想到了优化。
根据干瞪眼大法,我们惊奇地发现,后缀串\(i\)与后缀串\(i+1\)只相差一个字符
废话,但暴力算法却又重新匹配了一遍,完全属于不必要的计算量,那么我们怎么消除这些冗余的计算量呢?
设后缀串\(i\)排名为\(j\)与排名为\(j-1\)的后缀串\(k\)的最长公共前缀为\(x\),因为\(i\)的字典序大于\(k\)的字典序且中间没有别的串,所以\(i+1\)的字典序大于\(k+1\)的且中间没有别的串。又因为\(i\)与\(k\)最长公共前缀为\(x\),所以\(i+1\)与\(k+1\)的最长公共前缀最少为\(x-1\),然后判断是否能继续扩展(大多情况不行),这样我们就避免了巨大的重复计算量。
后缀排序与高度数组的代码实现如下(代码锅点已标注):
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 1e6 + 5;
char s[MAXN];
int sa[MAXN] , rk[MAXN] , n , height[MAXN];
int x[MAXN] , y[MAXN] , cnt[MAXN] , t[MAXN];
void make_suffix() {
int m = 128;//由于小写字母的字典序最多那么多
for (int i = 1; i <= n; ++i) cnt[x[i] = s[i]] ++;//x储存的是每个后缀串中的离散化值
for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (int i = 1; i <= n; ++i) sa[cnt[x[i]]--] = i;//记录第一次桶排值
for (int k = 1; k <= n; k *= 2) { // 倍增法,每次求目前区间两倍位置的字典序离散化值
int tot = 0;
for (int i = n - k + 1; i <= n; ++i) y[++tot] = i;
for (int i = 1; i <= n; ++i) if(sa[i] > k) y[++tot] = sa[i] - k; // 这个地方有一点难理解,与存储的是1~n中扩展的位置的字典序从小到大排,即这个桶排思路为先排已知的,再按扩展串离散化值排已知离散化值相同的
for (int i = 1; i <= m; ++i) cnt[i] = 0;
for (int i = 1; i <= n; ++i) cnt[x[y[i]]] ++;
for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; --i) sa[cnt[x[y[i]]] --] = y[i];//因为y时从小到大,所以倒序取桶
tot = 1;
t[sa[1]] = 1;
for (int i = 2; i <= n; ++i) {
if(x[sa[i]] == x[sa[i - 1]] && x[sa[i] + k] == x[sa[i - 1] + k]) t[sa[i]] = tot;
else t[sa[i]] = ++tot;
}//更新离散化值,离散化值即为他的排名
if(tot >= n) break;//优化,如果每个人排名互不相同,那么我们则认为他是排序完成的
for (int i = 1; i <= n; ++i) x[i] = t[i];//更新
m = tot + 1;//注意更新m值,因为他的排名数字会增多,所以桶要变大
}
for (int i = 1; i <= n; ++i) rk[sa[i]] = i;//根据sa求rk
}
void make_height() {
int k = 0;
for (int i = 1; i <= n; ++i) {//按照原串顺序便利
if(k) k --;//这一次至少是上一次减一
int j = sa[rk[i] - 1];//找到与之匹配的串
while(s[i + k] == s[j + k]) k ++;//扩展
height[rk[i]] = k;//记录
}
}//复杂度分析:考虑最坏情况,k最多减n次,所以最多扩展2n次,根据分摊返还,所以他是O(n)
int main() {
scanf("%s" , s + 1);
n = strlen(s + 1);
make_suffix();
for (int i = 1; i <= n; ++i) printf("%d " , sa[i] - 1);
make_height();
putchar('\n');
for (int i = 1; i <= n; ++i) printf("%d " , height[i]);
return 0;
}
例2.1.2
这道题其实也可以用后缀数组做,但是怎么吸氧都过不了,毕竟倍增法求后缀排序常数太大了~~
回文子串本质上是一个串倒过来和原串一致,所以我们可以把主串倒过来,接到原串后面用特殊符号隔开,满足条件中(即相邻的这两个串分处特殊符号两端)的最大高度数组值就是答案~~
代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 1e7 + 5;
char s[MAXN];
int sa[MAXN] , rk[MAXN] , n , height[MAXN];
int x[MAXN] , y[MAXN] , cnt[MAXN] , t[MAXN];
void make_suffix() {
int m = 128;
for (int i = 1; i <= n; ++i) cnt[x[i] = s[i]] ++;
for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (int i = 1; i <= n; ++i) sa[cnt[x[i]]--] = i;
for (int k = 1; k <= n; k *= 2) {
int tot = 0;
for (int i = n - k + 1; i <= n; ++i) y[++tot] = i;
for (int i = 1; i <= n; ++i) if(sa[i] > k) y[++tot] = sa[i] - k;
for (int i = 1; i <= m; ++i) cnt[i] = 0;
for (int i = 1; i <= n; ++i) cnt[x[y[i]]] ++;
for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; --i) sa[cnt[x[y[i]]] --] = y[i];
tot = 1;
t[sa[1]] = 1;
for (int i = 2; i <= n; ++i) {
if(x[sa[i]] == x[sa[i - 1]] && x[sa[i] + k] == x[sa[i - 1] + k]) t[sa[i]] = tot;
else t[sa[i]] = ++tot;
}
if(tot >= n) break;
for (int i = 1; i <= n; ++i) x[i] = t[i];
m = tot + 1;
}
for (int i = 1; i <= n; ++i) rk[sa[i]] = i;
}
void make_height() {
int k = 0;
for (int i = 1; i <= n; ++i) {
if(k) k --;
int j = sa[rk[i] - 1];
while(s[i + k] == s[j + k]) k ++;
height[rk[i]] = k;
}
}
int main() {
int T = 0;
scanf("%d" , &T);
while(T -- > 0) {
scanf("%s" , s + 1);
if(s[1] == 'E') return 0;
memset(cnt , 0 , sizeof cnt);
n = strlen(s + 1);
s[n + 1] = '#';
for (int i = 1; i <= n; ++i) s[n + 1 + i] = s[n - i + 1];
n = n * 2 + 1;
make_suffix();
make_height();
int ans = 0;
for (int i = 1; i <= n; ++i) {
if((sa[i] < n / 2 && sa[i - 1] > n / 2) || (sa[i - 1] < n / 2 && sa[i] > n / 2)) {
ans = max(ans , height[i]);
}
}
printf("%d\n" , ans);
}
return 0;
}
例2.1.3
给定主串和模式串,求主串的第\(x\)个后缀串(下面叫他\(x\))与模式串的第\(y\)个后缀串(下面叫他\(y\))的最长公共前缀,多组询问。
首先,这道题显然可以用\(hash\)加二分暴力乱搞,而且跑得飞快,这里不多加赘述。
我们这里重点讲后缀数组的做法,我们把模式串接在后面,特殊字符隔开,进行后缀排序。
那么\(x\)的位置就是\(rk_x\),\(y\)的位置就是\(rk_y\),我们尝试将他们的\(LCP\)与高度数组挂钩。我们找不到一个\(height_i\)能够描述这两个串的相似度,但是在他们中间夹着有许多高度数组,我们尝试用他们求出答案。首先\(rk_y\)与前一个相同的前缀字符串为\(height_{rk_y}\),那么我们就只考虑这些字符,然后继续往前迭代,不难证出,答案就是这些后缀数组的最小值。那么我们怎么求这些最小值呢?很显然,这是一个\(RMQ\)问题,可以用倍增\(ST\)表解决。但我感觉这种做法可能不如\(hash\)效率高。。。
看了那么多,不如练道题吧:
3、Manacher
例2.3.1
之前我也讲过马拉车,但感觉讲得不是很好,下面重讲一遍。
暴力之前讲过了,不多说。这实际上也是一个根据暴力优化的算法~~
我们还是找到某一个字符为中心,然后向两端扩张。但是,我们找的是回文串,回文串是具有对称性质的,所以我们为什么不去借助之前计算出的结果呢?我们拓展的这个串大概率是包含在之前的计算出的回文串中的,我们可以知道这个串的中心位置,当前位置关于中心位置对称了一个点,而这个点所扩展的回文串在中心点所包含的回文串内的部分的长度必然也在当前串也能至少扩展出来,因为回文串具有对称性质,因此,我们可以先进行转移,然后暴力向外扩展,更新当前长度。而我们的中心串,最优的办法显然是一个能够到达最远的地方的一个回文串,这样能够保证我们的回文串具有绝对\(O(n)\)的性质,因为每一次拓展必然是一个从来没有扩展到达过的点~~
代码(不吸氧能过,吸氧后是第九优解)
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 1000005;
char s[MAXN] , a[MAXN << 1];
int n , cnt , f[MAXN << 1];
int main() {
int T;
scanf("%d" , &T);
while(T --> 0) {
memset(f , 0 , sizeof f);
int mid , len , maxl;
scanf("%s" , s + 1);
n = strlen(s + 1);
cnt = 0;
for (int i = 1; i <= n; ++i) {
a[++cnt] = s[i];
a[++cnt] = '#';
}
mid = 1;
len = 0;
maxl = 0;
for (int i = 2; i <= cnt; ++i) {
if(i <= mid + len) {
f[i] = min(mid + len - i , f[(mid << 1) - i]);
int j = i + f[i] + 1;
int k = i - f[i] - 1;
while(k >= 1 && j <= cnt && a[k] == a[j]) j ++ , k -- , f[i] ++;
if(f[i] > f[maxl]) {
maxl = i;
}
if(i + f[i] > len) {
mid = i;
len = f[i];
}
}
else {
int j = i + 1;
int k = i - 1;
while(k >= 1 && j <= cnt && a[k] == a[j]) j ++ , k -- , f[i] ++;
if(f[i] > f[maxl]) {
maxl = i;
}
if(i + f[i] > len) {
mid = i;
len = f[i];
}
}
}
mid = maxl;
len = f[mid];
if(a[mid] != '#' && len % 2 == 0) len ++;
else if(mid - len == 1 && mid != 1) len ++;
printf("%d\n" , len);
}
return 0;
}
4、Trie树
\(Trie\)树,即字典树,它的基本用法十分好理解,但是变种用法多种多样,难以琢磨,因此,本章主要讲解各种应用。
\(Trie\)树是用来储存大量字符串的,可以在很大程度上减少内存分配,同时也可以方便查找是否出现过。所以\(Trie\)树的本质实际上是一棵多叉树(若储存的是小写字母串则是一棵\(26\)叉树),但是如果按照正常储存就会浪费大量内存,那么\(Trie\)树是怎么解决的呢?我们可以采用动态开点的方式来储存,发现存在一个字母,在之前这个位置都没有出现过只需要建立一个新的节点就可以了。下面结合例题与代码理解就可以了。
例2.4.1
这是一道字典树的板子题,我们的目标就是检查是否存在一个数字串是另一个数字串的前缀。我们可以一边输入,一边在线建立一棵字典树,如果我们在为某一个串在字典树中建立信息的时候没有建立一个新的节点,证明该串是之前某一个串的子串(想一想为什么?)。此外,如果我们在建立信息的过程中经历过一个节点,且这个节点是一个数字串的结尾,证明之前有一个串是该串的前缀~~。
想必大家都还没有理解字典树的实现吧,我将在下面的代码中带领大家领略一下精神:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e5 + 5;
LL trie[MAXN][15] , tot = 1;
LL b[MAXN]; //b[i]表示i号节点是否是一个字符串的结尾。
void Insert(char s[] , bool &flag) {
LL u = 1 , tmp = tot , len = strlen(s); //一号节点是空节点,表示root
for (LL i = 0; i < len; ++i) {
LL c = s[i] - '0' + 1;
if(!trie[u][c]) trie[u][c] = ++tot;//如果没有存在过这个节点就建立
else if(i == len - 1) {
if(tot == tmp) flag = true; //如果没有建立新节点
}
u = trie[u][c];
if(b[u]) flag = true;//如果这个节点是结尾
}
b[u] = true;//记录结尾节点
}
int main() {
LL t;
scanf("%lld" , &t);
while(t --> 0) {
tot = 1;
memset(trie , 0 , sizeof trie);
memset(b , 0 , sizeof b);
LL n;
bool flag = 0;
scanf("%lld" , &n);
for (LL i = 1; i <= n; ++i) {
char s[15];
scanf("%s" , s);
Insert(s , flag);
}
if(flag) printf("NO\n");
else printf("YES\n");
}
return 0;
}
例2.4.2
这道题要求计算最大异或对,我们先考虑对于一个确定的数,异或哪一个数最大。
我们考虑异或的最本质特征:相同为假,不同为真。
那么我们可以对这些数的二进制进行建字典树,然后尽可能在字典树中从高位尽可能地寻找与自己差异大的二进制数。
而对于任意两个数我们只需要枚举\(n\)个数,对于每个数查找最大异或数,然后选择最大值。
代码如下:
#include <queue>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e5 + 5;
LL n , a[MAXN] , tot = 1;
LL c[MAXN << 4][2];
void Insert(LL x) {
queue <LL> q;
for (LL i = 30; i >= 0; --i) {
if(x & (1 << i)) q.push(1);
else q.push(0);
}
LL u = 1;
while(!q.empty()) {
LL k = q.front();
q.pop();
if(!c[u][k]) c[u][k] = ++tot;
u = c[u][k];
}
}
LL find(LL x) {
LL re = 0 , u = 1;
for (LL i = 30; i >= 0; --i) {
LL k = 0;
if(x & (1 << i)) k = 1;
if(c[u][!k]) {
re += (1 << i);
k = !k;
}
u = c[u][k];
}
return re;
}
int main() {
LL t;
scanf("%lld %lld" , &n , &t);
for (LL i = 1; i <= n; ++i) {
scanf("%lld" , &a[i]);
Insert(a[i]);
}
LL ans = 0;
for (LL i = 1; i <= n; ++i) {
LL x = ans;
ans = max(ans , find(a[i] ^ t));
if(ans == t) ans = x;
}
printf("%lld" , ans);
return 0;
}
例2.4.3
给定一棵带权树,最大的两个节点的异或路径。
首先,两个节点之间的路径唯一确定,及经过他们的\(LCA\)。
其次,两个相同的数异或起来等于\(0\),而\(0\)异或任意一个数结果为他本身,而任意一个节点到根节点的异或路径必然经过他的祖先。
因此,两个节点的异或路径即为他们到根节点的路径异或和的异或值。
我们预处理出根节点到每个节点的异或值,那么两个节点的异或最大值就是在预处理出来的这些根节点到节点的异或值中任选\(2\)个的异或最大值。那么这个问题又转化成了例2.4.2,代码就不用我给了吧。
三、简单数据结构
1、堆
堆这个东西很简单,我只需要领略一下精神就好~~
堆这个东西他本质是一棵完全二叉树,可以用数组来模拟,根据完全二叉树的性质,当前节点编号\(>>1\)即为父亲节点,当前节点编号\(>>1 | 0\)为左儿子,\(>> 1 | 1\)为右儿子。他是用来维护极值的,具体方法是定义每一个节点的值都比他子树的节点的值要大(小),这样根节点就是最大(小)值辽。
关于实现也只用领略一下精神。我们每一次插入节点的时候把他放在数组末尾,检测是否比根节点大(小),为真则交换。删除操作即把节点变成叶子节点后删除,即与数组末元素交换位置,然后检查是否能上移或下移。
另外,我们伟大的先辈已经为我们打包好了这个数据结构,存放在\(queue\)里面的,叫做:
priority_queue
接下来我们讲解一下最为经典的两大应用
例3.1.1
这是堆最经典的应用,我们有两个有序表:\(a\)和\(b\),则他们有\(n^2\)种组合方案得到下表
\(a_1 + b_1\) , \(a_1 + b_2\) , ... \(a_1 + b_n\)
\(a_2 + b_1\) , \(a_2 + b_2\) , ... \(a_2 + b_n\)
......
\(a_n + b_1\) , \(a_n + b_2\) , ... \(a_n + b_n\)
我们需要在上表中找到前\(n\)小的,我们发现,在每一行中,编号越小值必然越小,但不同行之间有时无法比较,所以我们可以维护堆不同行的行开头,每次得出最小的一个,然后更新该行行头加入堆内,代码如下:
#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e6 + 5;
LL c[MAXN] , a[MAXN] , b[MAXN] , n;
struct node {
LL id , data;
node () {}
node (LL x , LL y) {
id = y;
data = x;
}
};
struct cmp {
bool operator() (node &x , node &y) {
return x.data > y.data;
}
};
priority_queue <node , vector <node> , cmp> q;
int main() {
scanf("%lld" , &n);
for (LL i = 1; i <= n; ++i) scanf("%lld" , &a[i]);
for (LL i = 1; i <= n; ++i) scanf("%lld" , &b[i]) , c[i] = 1;
for (LL i = 1; i <= n; ++i) q.push(node(a[1] + b[i] , i));
for (LL i = 1; i <= n; ++i) {
node x = q.top();
q.pop();
printf("%lld\n" , x.data);
c[x.id] ++;
q.push(node(a[c[x.id]] + b[x.id] , x.id));
}
return 0;
}
看了这道例题不如做一做这一道双倍经验~~
例3.1.2
暴力算法是建立有序数组,二分插入,寻找中位数,复杂度为\(O(n^2)\)
我们可以建立两个堆,一个是小根堆,一个是大根堆,要求大根堆中的每一个元素都比小根堆中的小,这样的两个堆组成的数据结构叫做对顶堆,我们需要保证上述条件成立的同时,我们还要调整堆内元素个数,使得大根堆的元素个数刚好比小根堆多\(1\)或\(0\)个,这样,大根堆内元素即为中位数。
下面给出模板:
struct opposite_vertex_heap {
priority_queue <int , vector <int> , greater<int> > U;
priority_queue <int , vector <int> , less <int> > D;
void insert(int x) {
if(D.size() == 0) D.push(x);
else if(x > D.top()) U.push(x);
else D.push(x);
if(U.size() == D.size() + 1) {
D.push(U.top());
U.pop();
}
else if(U.size() + 2 == D.size()) {
U.push(D.top());
D.pop();
}
}
int find_mid() {return D.top();}
}a;
2、树状数组
树状数组是一个十分神奇的东西,用过的人都说好。树状数组本身是只支持单点修改,区间查询的操作的,但是经过一番推式子瞎搞就可以得到一些极其美妙的方法实现。
基础应用:例3.2.1
本题要求单点修改区间查询,关于区间查询我们第一反应想到前缀和。但是前缀和是静态的,每一次修改都需要\(O(n)\)的时间去改变整个前缀和数组。那么我们直接模拟吧,但是查询却有需要近似\(O(n)\)的时间。那么我们能不能把两种方法综合一下呢?还是之前的那句老话,要想优化一种算法就要先找他的缺点。
让我们一起来怼前缀和吧
对于前缀和,他之所以慢,是因为每一次修改数值都需要对它后面所有的元素的值都会产生变化。变化的存在是必然的,那么我们能否让他少产生一些变化呢?怎么少产生变化呢?我们可以让后面的有一些元素不控制到他自己,只控制部分,代价就是查询速度变慢。现在我们已经有一个基本的雏形了,我们要去充实它。
现在问题来了,一个元素不一定控制它之前的某些元素,那么控制它之前的哪些元素呢?我们先假定他控制的是包含自己的一段连续区间这是一种递归的思想:我们需要求前\(x\)个数的前缀和,而这第\(x\)号元素控制着部分,我们需要在\(O(1)\)的时间找到能够接续他控制区间的元素。同时在单点修改的时候,我们也需要在\(O(1)\)的时间找到最近的能够控制它的元素。
我们不妨想一想二进制,对于一个区间我们可以用二进制的方法把他拆分成很多大小不相同的小块,例如\(11\),我们可以把他变成\(1\),\(2\),\(8\)大小的区间。我们尝试每个点覆盖一个大小为分解出来最小的块的大小,例如\(11\),我们就只覆盖大小为\(1\)的块。我们把这些数的覆盖区间画出来如下图:
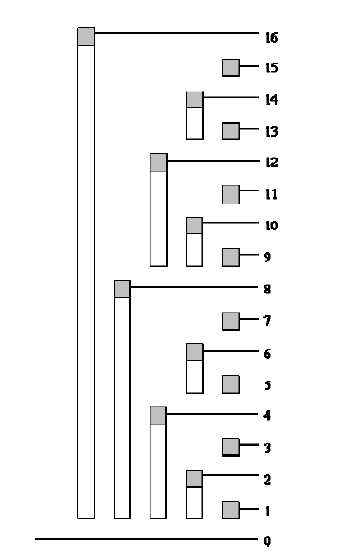
我们发现神奇的规律:对于每一个节点,都会在接下来的节点中都会出现一个和他覆盖的节点完全相同的一个覆盖,唯一不同的是,结尾的那一个节点覆盖了这两个相似的覆盖。这是一个非常奇妙的递归,从\(1\)开始,复制一个自己,并让他的结尾覆盖自己,然后继续复制,覆盖,源源不断,永无止境。
根据以上规律,我们发现,第一个覆盖他的节点就是他加上他覆盖的区间的大小,问题迎刃而解。
下面结合代码理解:
#include <cstdio>
typedef long long LL;
const int MAXN = 1e7 + 5;
LL c[MAXN] , n , q;
LL lowbit(LL x) {return x & (-x);}
void update(LL x , LL y) {
for (; x <= n; x += lowbit(x)) c[x] += y;
}
LL find(LL x) {
LL re = 0;
for (; x > 0; x -= lowbit(x)) re += c[x];
return re;
}
int main() {
scanf("%lld %lld" , &n , &q);
for (LL i = 1; i <= n; ++i) {
LL x;
scanf("%lld" , &x);
update(i , x);
}
for (LL i = 1; i <= q; ++i) {
LL x;
scanf("%lld" , &x);
if(x == 1) {
LL y , z;
scanf("%lld %lld" , &y , &z);
update(y , z);
}
else {
LL y , z;
scanf("%lld %lld" , &y , &z);
printf("%lld\n" , find(z) - find(y - 1));
}
}
return 0;
}
上面就是树状数组最最基础的应用了,树状数组的作用特别多(例如用差分实现区修单查)而且代码简单常数优秀,因此就有了一句话:大佬们都喜欢树状数组,菜的人才用线段树。像我这种菜鸡肯定只会用线段树了~。
下面我给大家简单分享一下树状数组的妙用
区间修改,区间查询:例3.2.2
区间修改嘛,自然而然地想到了差分嘛,定义一个差分数组\(a\),区间查询怎么办呢?
来来来,我们来玩一玩式子,查询区间\([x,y]\)的和想当于:
\(\sum_{i=x}^{y}\sum_{j=1}^{i}a_i\)
然后我们可以进行一波等效替代的转化:
\(x \times \sum_{i=1}^{x}a_i + \sum_{i=x+1}^{y}a_i \times(i-x+1)\)
即:
\(x\times\sum_{i=1}^{x}+\sum_{i=x+1}^{y}-\sum_{i=x+1}^{y}a_i\times x\)
因此我们只用维护两个树状数组,一个用来维护\(a_i\)的前缀和和\(a_i \times i\)的前缀和就好了,代码就不给了~。
这里只是一个引子,很多题都需要这样的式子推导,也正式因为这些式子的推导使数据结构维护各种奇奇怪怪的东西(比如二维差分前缀和之类的)变成了可能。
例3.2.3
首先a是确定的,我们考虑对于一组询问的答案如何计算。由于a和b都比c不知道高明到哪里去了,所以b要么是a祖先,要么是a的孩子。
当b是a的k级以内祖先时,答案就是\(\min (dep_a - 1 , x) \times (siz_a - 1)\)
当b是a的k级以内儿子时,答案就是 $ \sum siz_b - 1 $
问题就在于如何在log时间内解决第二个问题,我很快就放弃了思考,因为我发现离线可以更加轻松。
我们先记录哪些节点需要找到属于他的三元组,用vector记录起来,在遍历到他时统计一波答案即可。
我们动态维护一个树状数组,储存深度为\(i\)的节点的\(siz\)和,由于这里满足区间可加性,那么我们统计答案时就是 总共的满足深度的减去子树以外满足深度,而后者在我们刚刚到达统计答案的节点的时候就可以进行一波记录,遍历完子树再去记录结果。
见代码(代码后面有正文,不要跑~)
#include <cstdio>
#include <vector>
#include <algorithm>
typedef long long LL;
using namespace std;
const int MAXN = 3e5 + 5;
void read(LL &x){
LL f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
LL head[MAXN] , to[MAXN << 1] , nxt[MAXN << 1] , cnt;
LL tr[MAXN << 1] , ans[MAXN] , siz[MAXN] , dep[MAXN];
LL n , q;
struct node {
LL k , id;
node () {}
node (LL K , LL I) {
k = K;
id = I;
}
};
vector <node> que[MAXN];
void add(LL u , LL v) {nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;}
void update(LL x , LL y) {
for (; x <= n * 2; x += (x & (-x)))
tr[x] += y;
}
LL find(LL x) {
LL res = 0;
for (; x; x -= (x & (-x))) {
res += tr[x];
}
return res;
}
void dfs1(LL x , LL fa) {
dep[x] = dep[fa] + 1;
siz[x] = 1;
for (LL i = head[x]; i; i = nxt[i]) {
if(to[i] == fa) continue;
dfs1(to[i] , x);
siz[x] += siz[to[i]];
}
}
void dfs(LL x , LL fa) {
update(dep[x] , siz[x] - 1ll);
for (LL i = 0; i < que[x].size(); ++i) {
ans[que[x][i].id] = -1ll * (find(dep[x] + que[x][i].k) - find(dep[x]));
ans[que[x][i].id] += min(dep[x] - 1ll , que[x][i].k) * (siz[x] - 1ll);
}
for (LL i = head[x]; i; i = nxt[i]) {
if(to[i] == fa) continue;
dfs(to[i] , x);
}
for (LL i = 0; i < que[x].size(); ++i) {
ans[que[x][i].id] += find(dep[x] + que[x][i].k) - find(dep[x]);
}
}
int main() {
read(n);read(q);
for (LL i = 1ll; i < n; ++i) {
LL u , v;
read(u);read(v);
add(u , v);
add(v , u);
}
for (LL i = 1ll; i <= q; ++i) {
LL p , k;
read(p);read(k);
que[p].push_back(node(k , i));
}
dfs1(1 , 0);
dfs(1 , 0);
for (LL i = 1ll; i <= q; ++i) {
printf("%lld\n" , ans[i]);
}
return 0;
}
当然,这道题同样可以用dsu来做,但复杂度显然会多一只dsu自带的log,所以他不是最优解。这道题不像统计类似于颜色种数的题,这道题满足区间可加性,即你可以把总共的答案减去之前算的答案,但是类似于颜色种数之流,自身子树和总共答案可能都包含同种颜色,因此不能直接相加减而应该依次减去每种颜色个数,然后算非0数个数。但这样复杂又退化成n方了,所以此时dsu就是一个比较优秀的做法。
3、线段树
线段树与树状数组功能类似,但相比之下,线段树使用起来更加方便灵活,同时也更易于去理解,也是比较重要的几个基础数据结构之一。
下面从基础开始讲述:
储备知识 : 二叉树
二叉树
满二叉树定义 : 一棵深度为k且有\(2 ^ {k} \qquad-1\)个节点(k >= 1)(即深度为k的二叉树的最多节点树)如图:
此时,我们就能对完全二叉树进行定义 :
深度为k的二叉树当且仅当其每一个节点都与深度为k的满二叉树的节点编号一一对应时,称其为完全二叉树如图:
为什么要讲这个鬼东西呢?因为完全二叉树有一个用起来非常舒服的性质,能帮我们找到一个结点的左右孩子:
若2 * i (该二叉树任意结点编号) > n (该二叉树的结点数) , 则该节点无左孩子 , 否则则左孩子编号为2 * i。
这样一来,我们就能用一个数组存储一个完全二叉树了
现在进入正题
关于线段树
线段树的本质就是一棵完全二叉树,它的叶节点存储单点的数据,而每一个结点则归纳它所包含区间所有叶节点的数据,而这里其实是采用的分治的思想,可以在短时间内获取到一个区间内的所需要的数据。线段树大概长这个样子。

线段树的基操
线段树的构建
那么我们怎么去构建一棵线段树呢?
由于树是递归定义的,所以我们可以采用递归建树,同时利用前面讲到的完全二叉树的性质来找到子节点进行建树,最后再根据自己的两个子区间计算得到自己这个大区间的数据就可以了~。
见代码(构造一棵记录区间和的线段树):
void build(int l , int r , int now) {
if(l == r) {
cnt ++;
tree[now] = a[cnt];
return;
}
int mid = (l + r) / 2;
build(l , mid , now * 2);
build(mid + 1 , r , now * 2 + 1);
tree[now] = tree[now * 2] + tree[now * 2 + 1];
}
单点修改
不断递归,保证下一个节点的区间包含目标节点,直到到达叶子节点为止,然后进行修改,并在递归返回后重新维护当前区间的一些信息。
见代码 :
void update(LL l , LL r , LL now , LL x , LL y) { // 将编号为x的点修改为y
if(l == r) {
tree[now] += y;
return;
}
LL mid = (l + r) / 2;
if(x <= mid) update(l , mid , now * 2 , x , y);
else if(x > mid) update(mid + 1 , r , now * 2 + 1 , x , y);
tree[now] = tree[now * 2] + tree[now * 2 + 1];
}
区间查询
此时线段树的优势就彻底展示出来了。
我们可以找到线段树中的节点包含的区间,使得这些区间完全包含在我们目标查询的大区间当中,把这些节点我数据提取出来,然后按照合并左右儿子区间的方法合并提取出来的区间,合并完成后的信息就是我们的目标答案。详见代码。
LL get_sum(LL l , LL r , LL now , LL x , LL y) { //查询[x , y] 区间的每一个数的和
if(x <= l && y >= r) return tree[now]; //当当前结点被完全笼罩则返回数据
LL mid = (l + r) / 2 , _sum = 0;
if(x <= mid) _sum += get_sum(l , mid , now * 2 , x , y); //当区间与左孩子有交集 , 查询左区间
if(mid < y) _sum += get_sum(mid + 1 , r , now * 2 + 1 , x ,y); //当区间与右区间有交集 , 查询右区间
return _sum;
}
区间修改
这才是重头戏 , 怎么改呢?把每个数揪出来改??
像这样??
void update(int now,int l,int r,int q_l,int q_r,int x){
if(l==r)sum[now]=sum[now]+x;else{
int mid=(l+r)/2;
if(q_l<=mid)update(now*2,l,mid,p_l,p_r,x);
if(q_r>mid)update(now*2+1,mid+1,r,p_l,p_r,x);
sum[now]=sum[now*2]+sum[now*2+1];
}
}
实际上这样子比暴力还不如……
根据人类的本质--贪心,得到,我们为什么要在每次修改的时候完成修改呢,为什么不把这些需要修改的信息储存起来,等到要查询的时候再去统一修改呢???
于是伟大的创造产生了--lazy_tag,它就是储存该节点所包含区间的每个节点都要修改时的修改信息总和,而当我们需要拜访这个节点子区间的时候就可以把这些信息传递给它的两个子区间就行了~。
具体操作如下 :
void push_up(LL now) {
tree[now] = tree[now * 2] + tree[now * 2 + 1];
}
void push_down(LL l , LL r , LL now) {
if(tag[now]) { //如果自己加了
LL mid = (l + r) / 2;
tree[now * 2] += (mid - l + 1) * tag[now]; // 那么修改维护孩子的值
tree[now * 2 + 1] += (r - mid) * tag[now];
tag[now * 2] += tag[now]; //记录儿子加的,方便传给孙子
tag[now * 2 + 1] +=tag[now];
tag[now] = 0;
push_up(now); // 顺手维护好习惯
}
}
void update(LL l , LL r , LL now , LL x , LL y , LL t) {
if(x <= l && y >= r) {
tree[now] += (r - l + 1) * t; // 发现完全笼罩再要修改区间内,直接修改结点内容
tag[now] += t; //记录修改内容,方便往两个孩子处传递信息
return;
}
LL mid = (l + r) / 2;
push_down(l , r , now); //既然即将遍历孩子 , 顺手将自己加的东西传给孩子
if(mid >= x) update(l , mid , now * 2 , x , y , t);
if(mid < y) update(mid + 1 , r , now * 2 + 1 , x , y , t);
push_up(now); // 养成好习惯,顺手维护
}
例3.3.1 逆序对
这里讲解一下线段树或树状数组的另类应用。
求解逆序对,即求解对于每一个\(i\)的\(i < j\) 而 \(a_i > a_j\)的个数,那么我们可以把线段树或者树状数组维护的不是一个序列,而是一个桶,那么就很简单了,我们倒序地把数字装入这样的桶内,然后就是查询\(1 ~ a_i\)之间数字的个数就好了,由于树状数组和线段树的查询复杂度都是\(\log n\)的,因此,就可以快速求解逆序对了,代码就不放了。
线段树的妙用特别多,但万变不离其中,重在一个转化,要求把一些事情转化成为对区间的操作,而这些还是要在做题的过程中去感受,所以这里就不赘述了,如果有同学想要一些好题,这里提供一条友链。
4、树链剖分
dfs序
在一棵树上,我们常常会遇到求解一个节点的子树相关数据(例如求和)并涉及修改,那么我们该怎么办呢?
想到维护区间元素的值和修改,我们最先想到的就是树状数组和线段树,但是这两个神奇的数据结构都是维护一个序列的。于是,我们考虑将一棵树转换成一个序列并与线段树和树状数组有机结合,进而达到我们的目的。而将一棵树有机改造成一个序列,我们首先就可以想到二叉树中的先序遍历,中序遍历和后序遍历,根据遍历顺序转化成一个有规律的序列。显然,对于一棵普通的树是不存在中序遍历的,于是我们就可以对于一棵树使用先序遍历和后序遍历的方式转化成一个序列,我们对于这个序列分析性质我们可以发现,对于一棵子树,他所处的遍历位置必然是连续的,所以我们只需要记录一个节点在遍历序中的位置和子树大小,我们就可以在\(\log n\)的时间内完成操作。这就是我们的\(dfs\)序,当然,根据广大人民群众的习惯,大家都是按先序遍历的方式转化为序列的。
下面给出模板代码:
例3.4.1
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 1e6 + 5;
int a[MAXN] , dfn[MAXN] , cnt , size[MAXN];
long long d[MAXN];
vector <int> G[MAXN];
int n , m , r;
void read(int &x){
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
void update(int x , int y) {
for (; x <= n; x += (x & (-x))) {
d[x] += y;
}
}
long long find(int x) {
long long re = 0;
for (; x; x -= (x & (-x))) {
re += d[x];
}
return re;
}
void dfs(int x , int fa) {
dfn[x] = ++cnt;
update(cnt , a[x]);
size[x] = 1;
for (int i = 0; i < int(G[x].size()); ++i) {
if(G[x][i] == fa) continue;
dfs(G[x][i] , x);
size[x] += size[G[x][i]];
}
}
int main() {
read(n);read(m);read(r);
for (int i = 1; i <= n; ++i) read(a[i]);
for (int i = 1; i < n; ++i) {
int u , v;
read(u);read(v);
G[u].push_back(v);
G[v].push_back(u);
}
dfs(r , -1);
// printf("1\n");
for (int i = 1; i <= m; ++i) {
int k;
read(k);
if(k == 1) {
int x , y;
read(x);read(y);
update(dfn[x] , y);
}
else {
int x;
read(x);
printf("%lld\n" , find(dfn[x] + size[x] - 1) - find(dfn[x] - 1));
}
}
return 0;
}
树链剖分
先看一道例题:
树链剖分是与dfs序有很多相似的地方,他们都是按照dfs的顺序给每个节点打上时间戳,从而实现树上规模操作,但是他比dfs序更加精细化。我们有时会遇到将树上两点间的简单路径的点的权值进行修改和查询,那么我们怎么办呢?想到两点间的简单路径,我们很自然地就想到了LCA,于是我们想要这些在一条链上的点的在线段树上位置是连续的。但是我们显然不可能让每一条链都是连续的,于是我们考虑在这棵树中选取尽量长的许多条链(这么选重链的原因在下面会介绍),使得这些链的id是连续的。我们姑且称这些链为重链,而重链中的一条边,我们姑且称其为重边。很显然,为了使一条重链中的点在线段树中的坐标是连续的,每一个节点只能将他的一个儿子与他的连边为重边。为了使我们的重链尽可能长,我们贪心地在每一个节点与他子树最大的一个儿子进行连边。那么现在就只剩下一个问题,如何求解LCA?我们只需要记录一个节点所在重链的链头,两个节点不断往上爬,同时查询修改,知道两个节点在同一条重链上,或者在同一个点上那么就可以结束操作了。
根据我们之前所讲到的dfs序的铺垫,那么对于子树的操作就很简单了,毕竟树链剖分是升级版的dfs序嘛。
关于树剖LCA的复杂度证明:
我们每次选取子树最大的一个儿子作为重儿子链接重边,那么为什么LCA的复杂度就是log级别的呢?我们可以分析他走重边/轻边的数量,我们发现,节点每一个轻儿子的子树大小都不会大于该子树大小的一半(否则他就是重儿子),因此,我们每走一条轻边数据规模都会缩小一半,所以我们最多会走\(log_{2}^{n}\)条轻边,而每走一条重链,就会走一条轻边,所以就是log级别的复杂度了。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
#define int long long
const int MAXN = 2e6 + 5;
inline void read(int &x){
x=0;char s=getchar();
while(s<'0'||s>'9'){s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
}
inline void write(int x) {
if(x <= 9) {
putchar(x + '0');
return;
}
write(x / 10);
putchar(x % 10 + '0');
}
int w[MAXN] , siz[MAXN] , hes[MAXN] , fa[MAXN] , deep[MAXN];
int cnt , id[MAXN] , tree[MAXN] , top[MAXN] , tag[MAXN];
int head[MAXN] , to[MAXN] , _next[MAXN];
int n , m , r , p;
inline void push_down(int l , int r , int x) {
if(tag[x]) {
int mid = (l + r) >> 1;
tree[x << 1] = (tree[x << 1] + (mid - l + 1) * tag[x] % p) % p;
tree[x << 1 | 1] = (tree[x << 1 | 1] + (r - mid) * tag[x] % p) % p;
tag[x << 1] = (tag[x << 1] + tag[x]) % p;
tag[x << 1 | 1] = (tag[x << 1 | 1] + tag[x]) % p;
tag[x] = 0;
}
}
inline void update1(int l , int r , int now , int x , int y) {
if(l == r) {
tree[now] = y;
return;
}
int mid = (l + r) >> 1;
if(x <= mid) update1(l , mid , now << 1 , x , y);
else update1(mid + 1 , r , now << 1 | 1 , x , y);
tree[now] = (tree[now << 1] + tree[now << 1 | 1]) % p;
}
inline void update2(int l , int r , int now , int x , int y , int z) {
if(l >= x && r <= y) {
tree[now] = (tree[now] + (r - l + 1) * z % p) % p;
tag[now] = (tag[now] + z);
return;
}
push_down(l , r , now);
int mid = (l + r) >> 1;
if(x <= mid) update2(l , mid , now << 1 , x , y , z);
if(y > mid) update2(mid + 1 , r , now << 1 | 1 , x , y , z);
tree[now] = (tree[now << 1] + tree[now << 1 | 1]) % p;
}
inline int find_sum(int l , int r , int now , int x , int y) {
if(l >= x && r <= y) {
return tree[now];
}
push_down(l , r , now);
int mid = (l + r) >> 1 , re = 0;
if(x <= mid) re = (re + find_sum(l , mid , now << 1 , x , y)) % p;
if(y > mid) re = (re + find_sum(mid + 1 , r , now << 1 | 1 , x , y)) % p;
return re;
}
inline void dfs1(int x , int f) {
fa[x] = f;
siz[x] = 1;
for (register int i = head[x]; i != 0; i = _next[i]) {
if(to[i] == f) continue;
dfs1(to[i] , x);
siz[x] += siz[to[i]];
if(siz[to[i]] > siz[hes[x]]) hes[x] = to[i];
}
}
inline void dfs2(int x , int _top , int f) {
if(x == 0) return;
top[x] = _top;
id[x] = ++cnt;
deep[x] = deep[f] + 1;
update1(1 , n , 1 , cnt , w[x]);
dfs2(hes[x] , _top , x);
for (register int i = head[x]; i != 0; i = _next[i]) {
if(to[i] == f || to[i] == hes[x]) continue;
dfs2(to[i] , to[i] , x);
}
}
inline void add(int x , int y , int z) {
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) swap(x , y);
update2(1 , n , 1 , id[top[y]] , id[y] , z);
y = fa[top[y]];
}
if(deep[x] > deep[y]) swap(x , y);
update2(1 , n , 1 , id[x] , id[y] , z);
}
inline int _sum(int x , int y) {
int re = 0;
while(top[x] != top[y]) {
if(deep[top[x]] > deep[top[y]]) swap(x , y);
re = (re + find_sum(1 , n , 1 , id[top[y]] , id[y])) % p;
y = fa[top[y]];
}
if(deep[x] > deep[y]) swap(x , y);
return re + find_sum(1 , n , 1 , id[x] , id[y]);
}
signed main() {
read(n);read(m);read(r);read(p);
for (register int i = 1; i <= n; ++i) read(w[i]);
for (register int i = 1; i < n; ++i) {
register int x , y;
read(x);read(y);
to[i] = y;
_next[i] = head[x];
head[x] = i;
to[i + n] = x;
_next[i + n] = head[y];
head[y] = i + n;
}
dfs1(r , 0);
dfs2(r , r , 0);
for (register int i = 1; i <= m; ++i) {
int c;
read(c);
if(c == 1) {
int x , y , z;
read(x);read(y);read(z);
add(x , y , z);
}
else if(c == 2) {
int x , y;
read(x);read(y);
write(_sum(x , y) % p);
putchar('\n');
}
else if(c == 3) {
int x , z;
read(x);read(z);
update2(1 , n , 1 , id[x] , id[x] + siz[x] - 1 , z);
}
else {
int x;
read(x);
write(find_sum(1 , n , 1 , id[x] , id[x] + siz[x] - 1));
putchar('\n');
}
}
return 0;
}
5、平衡树
6、分块
四、DP
基础dp别人写过了,所以就不写了qwq ,想要获得更多资源,请点这里
五、其他算法
1、dsu on tree
刚学完dsu,感觉这种思想好妙哦。其实dsu就是优雅的暴力,他借助树剖中一个节点最多走logn条轻边就可以到达根节点的思想从而完成对于暴力的优化。
在一些需要的统计内容十分复杂的树上查询问题上,树形dp往往会空间时间双双爆炸(比如统计子树内的不同权值的节点个数),而区间不满足可加减性,所以我们也无法运用树状数组线段树在dfs序上统计之前所有的和之前多加的(关于这类做法见树状数组篇 谈笑风生),在这时我们dsu on tree就派上了用场。
虽然我们无法将整棵树的所有节点的完整结果保存起来,但我们可以保存需要输出的答案。所以我们完全可以暴力枚举树中每一个节点然后再遍历一遍其子树统计答案。但是,这样做复杂度显然是\(n^2\)的。仔细想,我们把自己儿子节点遍历过的又要遍历一遍很麻烦,而我们又不可能储存每一个儿子的状态,那么我们考虑只保存一个子节点的状态,其他子节点用某种方法统计完答案后就将状态所占用的空间归还,在计算的时候再暴力地去遍历一遍。
总结一下:我们选取一个儿子作为特殊儿子最后遍历(否则会让普通节点的答案计算发生混淆)计算状态和答案,可以开设全局变量来达到保存状态的目的,其中只保存需要特殊儿子的状态(因为在dsu on tree 问题中你无法区分哪些是属于自己子树的答案),剩下的计算完就从全局变量中删除掉。
下面我们结合基础题目来理解一下:
例5.1.1
这是公认的dsu on tree的模板题,我们想要知道子树中出现次数最多的节点的权值和。
那么我们只用记录\(sum_x\)表示出现\(x\)次的颜色和,\(cnt_x\)表示第\(x\)种颜色的出现次数,同时维护一个\(res\)表示出现最大的次数就可以了~
请自行结合代码理解
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e5 + 5;
int n , c[MAXN];
int head[MAXN] , to[MAXN << 1] , nxt[MAXN << 1] , tot , son[MAXN] , siz[MAXN];
void add(int u , int v) {nxt[++tot] = head[u];head[u] = tot;to[tot] = v;}
void dfs1(int x , int fa) {
siz[x] = 1;
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa) continue;
dfs1(to[i] , x);
siz[x] += siz[to[i]];
if(siz[son[x]] < siz[to[i]]) son[x] = to[i];
}
}
LL cnt[MAXN] , _sum[MAXN] , res , ans[MAXN];
void cal(int x , int fa , int he , int f) {
if(f == 1) {
_sum[cnt[c[x]]] -= c[x];
cnt[c[x]] ++;
_sum[cnt[c[x]]] += c[x];
res = max(res , cnt[c[x]]);
}
else if(f == -1) {
_sum[cnt[c[x]]] -= c[x];
cnt[c[x]] --;
_sum[cnt[c[x]]] += c[x];
}
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa || to[i] == he) continue;
cal(to[i] , x , he , f);
}
}
void dfs2(int x , int fa , int keep) {
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa || to[i] == son[x]) continue;
dfs2(to[i] , x , 0);
res = 0;
}
if(son[x]) dfs2(son[x] , x , 1);
cal(x , fa , son[x] , 1);
ans[x] = _sum[res];
if(!keep) cal(x , fa , 0 , -1);
}
int main() {
scanf("%d" , &n);
for (int i = 1; i <= n; ++i) scanf("%d" , &c[i]);
for (int i = 1; i < n; ++i) {
int x , y;
scanf("%d %d" , &x , &y);
add(x , y);
add(y , x);
}
dfs1(1 , 0);
dfs2(1 , 0 , 0);
for (int i = 1; i <= n; ++i) printf("%lld " , ans[i]);
return 0;
}
例5.1.2
求解节点与多少节点拥有共同的k级祖先,就等于该节点的k级祖先的k级儿子个数减一。
求解k级祖先还是使用倍增法比较的方便~
虽然是动态询问,但由于它没有强制在线所以离线起来一般会更简单。我们用一个vector数组记录一下每个节点需要求哪k级儿子的个数。
既然是求k级儿子的个数,那么我们一下子就想到了用\(dep_i\)维护深度为i的节点个数,dsu模板打完统计一波答案就好了。
自行理解代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 1e5 + 5;
int f[MAXN][25];
int head[MAXN << 1] , to[MAXN << 1] , nxt[MAXN << 1] , tot , deep[MAXN] , siz[MAXN] , son[MAXN];
vector <pair<int , int> > Q[MAXN];
void add(int u , int v) {nxt[++tot] = head[u];head[u] = tot;to[tot] = v;}
void dfs(int x , int fa) {
siz[x] = 1;
for (int i = 1; i <= 20; ++i) f[x][i] = f[f[x][i - 1]][i - 1];
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa) continue;
f[to[i]][0] = x;
deep[to[i]] = deep[x] + 1;
dfs(to[i] , x);
siz[x] += siz[to[i]];
if(!son[x] || siz[son[x]] < siz[to[i]]) son[x] = to[i];
}
}
int F(int x , int y) {
for (int i = 20; i >= 0; --i) {
if(y & (1 << i)) x = f[x][i] , y ^= (1 << i);
}
return x;
}
int n , m , ans[MAXN] , cnt[MAXN];
void cal(int x , int he , int f) {
if(f == 1) {
cnt[deep[x]] ++;
}
else {
cnt[deep[x]] --;
}
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == he) continue;
cal(to[i] , he , f);
}
}
void check(int x) {
for (int i = 0; i < Q[x].size(); ++i) {
int fir = Q[x][i].first , sec = Q[x][i].second;
ans[sec] = cnt[deep[x] + fir];
}
}
void dfs2(int x , int keep) {
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == son[x]) continue;
dfs2(to[i] , 0);
}
if(son[x]) dfs2(son[x] , 1);
cal(x , son[x] , 1);
check(x);
if(!keep) cal(x , -1 , -1);
}
int main() {
scanf("%d" , &n);
for (int i = 1; i <= n; ++i) {
int x;
scanf("%d" , &x);
add(x , i);
}
dfs(0 , 0);
scanf("%d" , &m);
for (int i = 1; i <= m; ++i) {
int x , k;
scanf("%d %d" , &x , &k);
int fa = F(x , k);
if(fa != 0) Q[fa].push_back(make_pair(k , i));
else ans[i] = 1;
}
dfs2(0 , 0);
for (int i = 1; i <= m; ++i) printf("%d " , ans[i] - 1);
return 0;
}
2、点分治
我们考虑这样一个问题,对于一棵树,我们需要求解这棵树上有多少条路径使得每条路径的权值和都为k。
那么我们先考虑对于一个点,经过它的权值和为k的路径有多少条?
我们显然可以dfs它的每一棵子树,求出子树中每一个节点距离当前根节点的距离x,检查之前遍历的子树中距离根节点距离为k-x的个数,然后计入总答案。
检查之前访问过的节点距离为k-x的节点个数可以用一个桶来存储,如果权值过大可以使用STL中的map。查询完这个点后我们可以删去当前点,这样这棵树就可以变成若干棵互相独立的树,对于这些树重复执行操作即可。
但是这样仍然有可能是\(O(n^2)\)的,因为如果数据是一条链,那么我们就会被卡到自闭。
那么我们考虑优化,我们发现每次进行dfs时,当前树的\(siz\)越大,复杂度越高。同时我们发现树的形态不同,复杂度也就不同(如果你每次从1号节点开始),同时我们发现树的边固定,选择哪一个节点是不会对答案产生影响的(即你选不同的点为根节点)。所以我们考虑每次选择一个优秀的根节点,使得删除它后它的儿子们产生的树的总复杂度最小。而单次查询的复杂度是\(O(siz_{now})\)的,因此我们如果每次选择重心,则至多会产生\(\log_{2}^{n}\)层,我们设处理单个节点的复杂度为\(x\)每层的复杂度最多是\(O(n \times x)\)的,因此最终的总复杂度就是\(O(n \times \log_{2}^{n} \times x)\)的了~。
例5.2.1
这道题与上述题目类似,我们只需要将上述问题中的map改为BIT,每次查询变成前缀和就可以了~。
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 4e4 + 5;
int n , head[MAXN] , to[MAXN << 1] , nxt[MAXN << 1] , cnt , edge[MAXN << 1];
void add(int u , int v , int w) {nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;edge[cnt] = w;}
int k , ans , tr[MAXN] , siz[MAXN] , rt , val , vis[MAXN];
void update(int x , int y) {
for (; x <= k; x += (x & (-x))) tr[x] += y;
}
int find(int x) {
int res = 0;
for (; x; x -= (x & (-x))) {
res += tr[x];
}
return res;
}
void get_root(int x , int fa , int num) {
siz[x] = 1;
int _max = 0;
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa || vis[to[i]]) continue;
get_root(to[i] , x , num);
_max = max(_max , siz[to[i]]);
siz[x] += siz[to[i]];
}
_max = max(_max , num - siz[x]);
if(_max < val) rt = x , val = _max;
}
int dis[MAXN];
void dfs(int x , int fa , int V) {
dis[++dis[0]] = V;
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa || vis[to[i]]) continue;
dfs(to[i] , x , V + edge[i]);
}
}
void work(int x) {
get_root(x , x , 0);
rt = val = 1e9;
get_root(x , x , siz[x]);
vis[rt] = 1;
for (int i = 0; i <= k; ++i) tr[i] = 0;
for (int i = head[rt]; i; i = nxt[i]) {
if(vis[to[i]]) continue;
dis[0] = 0;
dfs(to[i] , rt , edge[i]);
for (int j = 1; j <= dis[0]; ++j) {
if(dis[j] > k) continue;
ans += find(k - dis[j]);
}
for (int j = 1; j <= dis[0]; ++j) {
if(dis[j] > k) continue;
update(dis[j] , 1);
ans ++;
}
}
for (int i = head[rt]; i; i = nxt[i]) {
if(vis[to[i]]) continue;
work(to[i]);
}
}
int main() {
// freopen("P4178_1.in" , "r" , stdin);
scanf("%d" , &n);
for (int i = 1; i < n; ++i) {
int u , v , w;
scanf("%d %d %d" , &u , &v , &w);
add(u , v , w);add(v , u , w);
}
scanf("%d" , &k);
work(1);
printf("%d" , ans);
return 0;
}
接下来我们看一道有意思的。
例5.2.2
我们考虑使用点分治,先找到一条路径,然后判断它是否可行?
经过研究,我们发现一条路径是可行解,当且仅当它是多条平衡路径合并而来的,于是我们把以根节点出发的路径分为两种,一种是包含有平衡路径的路径,它的贡献就是在其他子树中能够与它组成平衡路径的路径数目。
另一种是不包含有平衡路径的路径,则它的贡献就是其他子树的路径中能与它组成平衡路径且包含有平衡路径的路径数。
最后特判一下以根节点为端点的可行解。
以上这些路径都可以用map维护快速求解。
细节见代码:
#include <map>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
void read(int &x){
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
const int MAXN = 1e5 + 5;
int head[MAXN] , to[MAXN << 1] , nxt[MAXN << 1] , cnt , edge[MAXN << 1];
void add(int u , int v , int w) {nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;edge[cnt] = w;}
int n , siz[MAXN] , rt , _max , vis[MAXN];
LL ans;
void get_siz(int x , int fa) {
siz[x] = 1;
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa || vis[to[i]]) continue;
get_siz(to[i] , x);
siz[x] += siz[to[i]];
}
}
void get_root(int x , int fa , int num) {
int res = 0;
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa || vis[to[i]]) continue;
get_root(to[i] , x , num);
if(siz[to[i]] > res) res = siz[to[i]];
}
if(num - siz[x] > res) res = num - siz[x];
if(res < _max) _max = res , rt = x;
}
map <int , int> M[2];
map <int , int> C;
struct node {
int val , ty;
}s[MAXN];
int tot;
void dfs(int x , int fa , int val) {
s[++tot].val = val;
if(C[val]) s[tot].ty = 1; //C有值则它包含有平衡路径
else s[tot].ty = 0;
if(val == 0 && C[val] > 1) ans ++;//特判与根节点合法的路径
C[val] ++;
for (int i = head[x]; i; i = nxt[i]) {
if(to[i] == fa || vis[to[i]]) continue;
dfs(to[i] , x , val + edge[i]);
}
C[val] --;
}
void work(int x) {
get_siz(x , 0);
rt = 0 , _max = 1e9;
get_root(x , 0 , siz[x]);
x = rt;vis[x] = 1;
C[0] = 1;
M[0].clear();M[1].clear();
for (int i = head[x]; i; i = nxt[i]) {
if(vis[to[i]]) continue;
tot = 0;
dfs(to[i] , x , edge[i]);
for (int j = 1; j <= tot; ++j) {
if(s[j].ty == 0) ans += M[1][-s[j].val];
//当不包含平衡路径时在以找到的路径中查找包含平衡路径且能与自己组成平衡路径。
else ans += M[0][-s[j].val] + M[1][-s[j].val];
//当包含时,能组成平衡路径中包不包含都可以
}
for (int j = 1; j <= tot; ++j) M[s[j].ty][s[j].val] ++;
}
for (int i = head[x]; i; i = nxt[i]) {
if(vis[to[i]]) continue;
work(to[i]);
}
}
int main() {
read(n);
for (int i = 1; i < n; ++i) {
int u , v , w;
read(u);read(v);read(w);
if(w == 0) w = -1;//这样做后,当一条路径是平衡路径则它的权值和为0
add(u , v , w);add(v , u , w);
}
work(1);
printf("%lld" , ans);
return 0;
}
3、CDQ分治
\(CDQ\)分治是由陈丹琪巨佬提出的,是用来解决多维偏序问题的,其中三维数点考察最为频繁。
二维偏序
经典题目就是求解逆序对个数。
逆序对是求解$pos_j < pos_i $ 并且 \(val_j > val_i\)的对数。
我们先把这个序列按照位置排序,然后以权值为关键字分治地对左半区间排一波序,对右半序列排一波序,然后合并。在合并的过程中我们统计答案。这样做有一个很方便的点,就是左区间的元素的\(pos\)一定比右区间的小,那么我们只需要统计对于每一个右区间中的元素,求取左区间中权值比它大的。由于左右区间权值又都是有序的,所以我们只需要知道左边区间中第一个比它大的元素的位置即可。而这个操作刚好可以在合并排序结果时做到,顺便统计一波答案即可。
由于这很简单,也不是重点,所以不给代码了 绝不是我找不到后懒得写
三维偏序
和二维数点类似,模板是对于每个\(i\)求取\(a_j \leq a_i,b_j \leq b_i,c_j \leq c_i\)的\(j\)的数量。
仿照二维数点的做法,我们已经找到了对于\(i\)在左区间中\(y_j > y_i\)的最小的\(j\),那么我们还要求取这\(j-l\)个元素中满足\(c_j \leq c_i\)的个数,很显然我们在找到\(j\)之前必然访问过他们一遍,所以我们只需要在访问了他们之后将他们加入BIT中,这样我们就可以直接查询前缀和统计答案。
例5.3.1
模板题,上文已经解释,这里直接看代码。
#include <map>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 1e5 + 5;
map <pair<int , int> , int> M[MAXN << 1];
struct node {
int a , b , c , num , id;
}tmp[MAXN] , a[MAXN];
bool cmp (node x , node y) {
if(x.b == y.b && x.a == y.a) return x.c < y.c;
if(x.a == y.a) return x.b < y.b;
return x.a < y.a;
}
void read(int &x){
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int N , k , n , f[MAXN] , tr[MAXN << 1];
node b[MAXN];
void update(int x , int y) {
for (; x <= k; x += (x & (-x))) tr[x] += y;
}
int find(int x) {
int res = 0;
for (; x; x -= (x & (-x))) res += tr[x];
return res;
}
void cdq(int l , int r) {
if(l == r) return;
int mid = (l + r) >> 1;
cdq(l , mid);cdq(mid + 1 , r);
int x = l , y = mid + 1 , t = 0;
while(x <= mid && y <= r) {
if(a[x].b <= a[y].b) {
b[++t] = a[x];
update(a[x].c , a[x].num);
x ++;
}
else {
b[++t] = a[y];
f[a[y].id] += find(a[y].c);
y ++;
}
}
if(y > r) {
for (int i = 1; i <= t; ++i) {
if(b[i].id <= mid) update(b[i].c , -b[i].num);
}
for (int i = x; i <= mid; ++i) b[++t] = a[i];
}
else {
for (int i = y; i <= r; ++i) {
b[++t] = a[i];
f[a[i].id] += find(a[i].c);
}
for (int i = 1; i <= t; ++i) {
if(b[i].id <= mid) update(b[i].c , -b[i].num);
}
}
for (int i = 1; i <= t; ++i) a[i + l - 1] = b[i];
}
int ans[MAXN];
int main() {
read(N);read(k);
for (int i = 1; i <= N; ++i) {
read(tmp[i].a);read(tmp[i].b);read(tmp[i].c);
M[tmp[i].a][make_pair(tmp[i].b , tmp[i].c)] ++;
}
for (int i = 1; i <= N; ++i) {
if(M[tmp[i].a][make_pair(tmp[i].b , tmp[i].c)]) {
a[++n] = tmp[i];
a[n].num = M[tmp[i].a][make_pair(tmp[i].b , tmp[i].c)];
M[tmp[i].a][make_pair(tmp[i].b , tmp[i].c)] = 0;
}
}
sort(a + 1 , a + 1 + n , cmp);
for (int i = 1; i <= n; ++i) a[i].id = i;
cdq(1 , n);
for (int i = 1; i <= n; ++i) ans[f[a[i].id] + a[i].num - 1] += a[i].num;
for (int i = 0; i < N; ++i) printf("%d\n" , ans[i]);
return 0;
}
例5.3.2
求解矩阵内的用户个数,考虑将矩阵转化为4个前缀和询问,然后就变成三维数点板子题。注意在加入树状数组时只加入查询操作的,统计答案时只统计询问操作的。
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
void read(int &x){
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
const int MAXQ = 2e5 + 5;
const int MAXN = 2e6 + 5;
struct node {
int x , y , ty , t , val;
node () {}
node (int X , int Y , int T , int Ti , int V) {
x = X;y = Y;ty = T;t = Ti;val = V;
}
}q[MAXQ] , b[MAXQ];
LL tr[MAXN] , ans[MAXN];
int n , cnt , T;
void update(int x , int y) {
for (; x <= n; x += (x & (-x))) tr[x] += y;
}
LL find(int x) {
LL res = 0;
for (; x; x -= (x & (-x))) res += tr[x];
return res;
}
void cdq(int l , int r) {
if(l == r) return;
int mid = (l + r) >> 1;
cdq(l , mid);cdq(mid + 1 , r);
int x = l , y = mid + 1 , t = 0;
while(x <= mid && y <= r) {
if(q[x].x <= q[y].x) {
b[++t] = q[x];
if(!q[x].ty) update(q[x].y , q[x].val);
x ++;
}
else {
b[++t] = q[y];
if(q[y].ty) ans[q[y].t] += find(q[y].y) * q[y].ty;
y ++;
}
}
for (int i = x; i <= mid; ++i) {
b[++t] = q[i];
if(!q[i].ty) update(q[i].y , q[i].val);
}
for (int i = y; i <= r; ++i) {
b[++t] = q[i];
if(q[i].ty) ans[q[i].t] += find(q[i].y) * q[i].ty;
}
for (int i = l; i <= mid; ++i) if(!q[i].ty) update(q[i].y , -q[i].val);
for (int i = 1; i <= t; ++i) q[i + l - 1] = b[i];
}
int main() {
int ty;
read(ty);read(n);
while(1) {
read(ty);
if(ty == 3) break;
else if(ty == 1) {
int x , y , a;
read(x);read(y);read(a);
q[++cnt] = node(x , y , 0 , 0 , a);
}
else {
int x1 , y1 , x2 , y2;
read(x1);read(y1);read(x2);read(y2);
T ++;
q[++cnt] = node(x1 - 1 , y1 - 1 , 1 , T , 0);q[++cnt] = node(x2 , y2 , 1 , T , 0);
q[++cnt] = node(x1 - 1 , y2 , -1 , T , 0);q[++cnt] = node(x2 , y1 - 1 , -1 , T , 0);
}
}
cdq(1 , cnt);
for (int i = 1; i <= T; ++i) printf("%lld\n" , ans[i]);
return 0;
}
例5.3.3
挺好的一道题,没那么板子。
如果不考虑矩阵内有没有其它稻草人,那么就是一道二维偏序的板子题。但是它有
那么我们考虑如何处理。首先对于一个点集\(j_k\),这些点都能与\(i\)组成合法矩阵。那么对于所有\(x_{j_p} < x_{x_q}\)都有\(y_{j_p} > y_{j_q}\),那么我们显然可以用CDQ分治,按\(x\)排序,用\(y\)进行CDQ,同时用单调栈维护左区间以访问过的元素,计算答案就是加上单调栈的元素个数?
一发交上去wa了。
我们再仔细考虑,在左区间我们维护了一个单调栈,进而排除了左区间元素对于\(i\)的遮挡,但是我们并没有屏蔽掉右区间的干扰。由于右区间不保证按照\(x\)递增,所以我们甚至不能用更改单调栈的方式进行处理。所以我们在计算右区间答案时维护一下对于所有\(x_j < x_i,y_j < y_i\)的\(y\)的最大值记为\(f_i\),而左区间中的元素想要与\(i\)形成答案\(y\)必然大于\(f_i\)且处于单调栈中,由于单调栈中元素的\(y\)值是单调递增的,因此我们可以二分一波求取答案。
代码:
#include <cstdio>
#include <algorithm>
using namespace std;
void read(int &x){
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
const int MAXN = 2e5 + 5;
int n;
struct node {
int x , y , id;
}a[MAXN] , b[MAXN] , s1[MAXN];
bool cmp(node x , node y) {
return x.x < y.x;
}
int t1 , f[MAXN];
long long ans;
int find(int k) {
int l = 1 , r = t1;
if(t1 == 0) return 0;
while(l + 1 < r) {
int mid = (l + r) >> 1;
if(s1[mid].y >= k) r = mid;
else l = mid;
}
if(s1[l].y >= k) return t1 - l + 1;
else if(s1[r].y >= k) return t1 - r + 1;
else return t1 - r;
}
void cdq(int l , int r) {
if(l == r) return;
int mid = (l + r) >> 1;
cdq(l , mid);cdq(mid + 1 , r);
int x = l , y = mid + 1 , t = 0;
t1 = 0;
int _max = 0;
while(x <= mid && y <= r) {
if(a[x].y < a[y].y) {
b[++t] = a[x];
while(t1 && s1[t1].x < a[x].x) t1 --;
s1[++t1] = a[x];
_max = max(a[x].y , _max);
x ++;
}
else {
b[++t] = a[y];
ans += find(f[a[y].id]);
f[a[y].id] = max(f[a[y].id] , _max);
y ++;
}
}
for (int i = x; i <= mid; ++i) b[++t] = a[i];
for (int i = y; i <= r; ++i) {
b[++t] = a[i];
ans += find(f[a[i].id]);
f[a[i].id] = max(f[a[i].id] , _max);
}
for (int i = 1; i <= t; ++i) a[i + l - 1] = b[i];
}
int main() {
read(n);
for (int i = 1; i <= n; ++i) read(a[i].x),read(a[i].y),a[i].id=i;
sort(a + 1 , a + 1 + n , cmp);
cdq(1 , n);
printf("%lld" , ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号