一种神奇的算法——单调队列
单调队列，顾名思义，就是一种队列。
在进入正文中，我们先来看这么一个问题：传送门
现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。
例如：
The array is [1 3 -1 -3 5 3 6 7], and k = 3
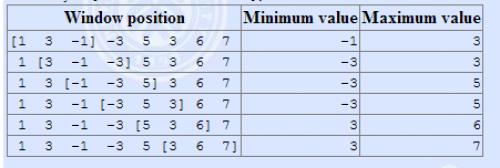
我们看到题面后，首先一个思路：暴力枚举！我们只要在\(k-n\)个数中枚举每一个最大值和最小值，最后取\(min\)或取\(max\)即可,代码如下
#include<iostream>
using namespace std;
int n,k;
int a[3000003];
int f[3000003];
int read() {
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
int main() {
n=read();k=read();
int l=0;
for(int i=1;i<=n;i++) a[i]=read();
for(int i=k;i<=n;i++) {
int maxn=-0xfffff,minx=0xfffff;
for(int j=i-k+1;j<=i;j++) {
if(a[j]>maxn) maxn=a[j];
if(a[j]<minx) minx=a[j];
}
cout<<minx<<" ";
f[++l]=maxn;
}
cout<<endl;
for(int i=1;i<=l;i++) cout<<f[i]<<" ";
}
然而理想是美好的，但是现实却是可怕的：
数据范围
\(50%\)的数据，\(n<=10^5\)
\(100%\)的数据，\(n<=10^6\)
对于这组数据，我们\(O(n*k)\)的方法只能拿\(70\)分(也许是我太蒟了) 所以我们要引进一种新的算法：单调队列
让我们先来理解一下单调队列的工作情况：
对于一个有框的队列中，我们每次读入一个数，
\(For\) \(example\)
有这么一组数：
\(1\) \(2\) \(3\) \(2\) \(5\) \(6\) \(7\) \(8\) \(9\) \(10\)
\(k=3\)
我们先读入\(1\),因为没有队首，就将他加入队。
接着，读入\(2\),\(2\)比\(1\)大且\(2\)在\(1\)之后\(,\)所以,我们将\(2\)入队，\(1\)出队
同理，我们接着读入\(3\)
可是，到了\(2\)之后，我们发现，\(2\)<\(3\),但是，\(2\)在\(3\)之后出现，所以，我们将\(2\)入队,所以\(,\)单调队列中变成了\(3\) \(2\)
接着,我们读入\(4\),因为\(4>3>2\),所以，我们将\(2\)与\(3\)出队，队列中只留下\(4\)
同理，我们后面就是不断地出队，入队的情况。
那有人可能会说，那\(2\)入队有什么用？
那我们再来看一组数据：
\(1\) \(2\) \(3\) \(2\) \(1\):\(k=2\)
这组数据，前面都与之前一样，
到\(1\)入队时,情况就发生了变化：
此时\(3\)由于\(k=2\)出队
那么,队首就变成了\(2\),那我们就输出\(2\),
所以这就是队首\(>\)读入的数,但仍要入队的原因
我们每读入一个数，就将他与队首比较\(:\)
如果队首比他小，那么队中比这个数小的都出队(这个数的可持久性比队中的强且这个数比队首大)
如果这个数比队首小，将他入队：
如果老的数超出范围，将他出队：
最终，队中留下的就是最大的或最年轻的,代码\(:\)
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define maxn 2000003
#define f(i,a,b) for(int i=a;i<=b;i++)
int a[maxn];
struct s{
int id;
int num;
};
s f[maxn];
int l=1;
int r;
int n,m;
int read() {
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
void write(int x) {
if(x<0) {
putchar('-');
x=-x;
}
if(x>9) write(x/10);
putchar(x%10+'0');
}
int main() {
n=read();m=read();
for(int i=1;i<=n;i++) {
a[i]=read();
}
int sum=0;
f(i,1,n+1) {
if(sum<m) sum++;
else if(l<=r) {
if(f[l].id+m<i) l++;
write(f[l].num);
putchar(' ');
}
while(f[r].num>=a[i]&&l<=r) r--;
f[++r].num=a[i];
f[r].id=i;
}
putchar('\n');
l=1;r=0;sum=0;
memset(f,0,sizeof(f));
f(i,1,n+1) {
if(sum<m) sum++;
else if(l<=r) {
if(f[l].id+m<i) l++;
write(f[l].num);
putchar(' ');
}
while(f[r].num<=a[i]&&l<=r) r--;
f[++r].num=a[i];
f[r].id=i;
}
}
\(PS:read\)和\(write\)可以忽略
