search
|—search()—|—添加一个列表变量Expend,存储每个小格扩展时为第几步,可打印出
| |—打印运动表
|—A*—|— heuristic()
|—Dynamic programming(动态规划)—|—Value编程
| |—应用于现实
| |—algorithm simulation
这是一种路径规划的算法,查找起点到终点路径的过程称为规划,这里讲的是规划的离散方法,用这些方法进行连续运动.

cost:每条路径花费的时间
每一个MOVE前、后移动,每一次Turn left、Turn right,都耗费一定成本单元
路径规划或搜索问题就是寻找最短的动作序列,将机器人从开始状态引导到结束状态

现在的问题是是否能找出起点到终点最短路径的程序。
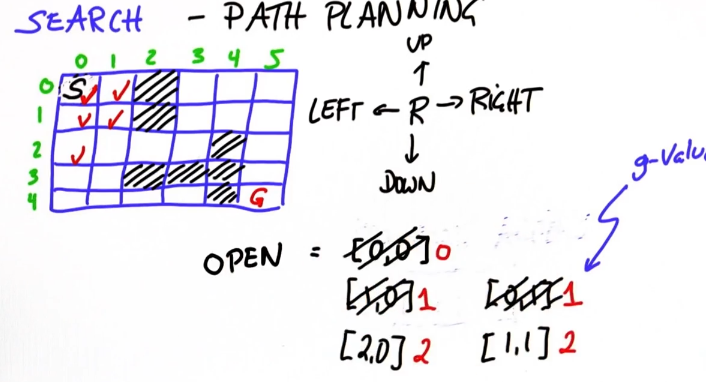
解决这个问题:给小格编号,在容器open中从起始点向周围扩展,并标上步数g值,当扩展到终点坐标时,最小的g值就是起点到终点的步数(秘诀:每次只展开最小的g值节点)
程序化这个过程:
# 编写search() 返回列表[g, row, col]. # 需要最终返回结果[11, 4, 5].到达不了返回'fail' grid = [[0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 1, 1, 1, 0], [0, 0, 0, 0, 1, 0]]
heuristic = [[9, 8, 7, 6, 5, 4],
[8, 7, 6, 5, 4, 3],
[7, 6, 5, 4, 3, 2],
[6, 5, 4, 3, 2, 1],
[5, 4, 3, 2, 1, 0]]
init = [0, 0] goal = [len(grid)-1, len(grid[0])-1] cost = 1 delta = [[-1, 0], # up [ 0,-1], # left [ 1, 0], # down [ 0, 1]] # right delta_name = ['^', '<', 'v', '>']
cost = 1 def search(grid,init,goal,cost): closed = [[0 for row in range(len(grid[0]))] for col in range(len(grid))] #为了避免重复展开,定义一个与网格大小相同的空网格 closed[init[0]][init[1]] = 1#将起始位置标志为关闭 expand = [[-1] * len(grid[0]) for i in grid]
action = [[-1] * len(grid[0]) for i in grid]
#置初值 x = init[0] y = init[1] g = 0
h = heuristic[x][y]
f = g + h open = [[g, x, y]] open = [[f, g, h, x, y]]
expand[x][y] = g
count = 0 #做两个标志值 found = False #找到目标时found置true resign = False #找不到目标并且没有其他地方可展开resign置true while not found and not resign: 检查open列表里是否有元素 if len(open) == 0: resign = True return "fail" else: #删除open最小g值以继续展开 open.sort() #递增排列 open.reverse() #颠转,因为pop是从头部弹出 next = open.pop() #弹出最小 #给要展开的x,y赋值,g必须在最前面 x = next[1] x = next[3] # x从0开始 y = next[2] y = next[4] # y从1开始 g = next[0] g = next[1]
expand[x][y] = count #将下面的那句改成这样
count += 1 # 将下面的这句移到这
expand[x][y] = expand_counter #检测是否达到目标 if x == goal[0] and y == goal[1]: found = True else: #这是没有达到,也是核心部分 for i in range(len(delta)): #遍历将每个动作都赋值给x,y x2 = x + delta[i][0] y2 = y + delta[i][1] if x2 >= 0 and x2 < len(grid) and y2 >=0 and y2 <len(grid[0]): #如果赋了动作的x,y仍然在网格内 if closed[x2][y2] == 0 and grid[x2][y2] == 0: #并且尚未标记(通过检查close),还有这个单元可以走 g2 = g + cost
h2 = heuristic[x2][y2]
f2 = g2 + h2 open.append([f2,g2, x2, y2]) closed[x2][y2] = 1
count += 1
action[x2][y2] = i#用[x2][y2]而不用[x][y]是因为后者代表扩展,前者代表回溯
policy = [[' '] * len(grid[0]) for i in grid]#action包含障碍物的所有方格的方向,非想要,所以要另外初始化一个用''填充的表格
x = goal[0] #标明终点并用*表示
y = goal[1]
policy[x][y] = '*'
while x != init[0] or y != init[1]: #从终点位置返回直到到达初始点为止
x2 = x - delta[action[x][y]][0]#通过从当前状态做减法来坐标回溯
y2 = y - delta[action[x][y]][1]
policy[x2][y2] = delta_name[action[x][y]]#将用二维向量表示的方向图像化
x = x2
y = y2
for row in policy:
print row
return policy
以下是打印代码
#print 'new open list:'
#for i in range(len(open))
# print '',open[i]
#print '---------------------'
#for i in range(len(expand)):
# print expand[i]
#print '---------------------'
expend step table
Expand是一个与网格大小相同的表格,它保存的是节点在哪个步骤展开的信息。从未展开过的标为-1,当一个节点展开时它会得到一个这个表格中唯一的步骤序号,比如下面这个例子步骤序号是0~22:

修改函数search(),以便返回一个名为expand的值的表,里面的元素是g,即此表将跟踪每个节点扩展时是在第几步。做少量修改,以下:
1.初始化一个与网格大小相同且初值全为-1的列表。
2.还需要一个名为count的变量来保持扩展步骤的数量。
3.在结束时,将expand [x] [y]的值设置为count的值,并将count递增1。
已在原代码中以红色代码添加
Print Path
打印出最终解决方案的路径,为此实现一个新的数据结构。

已在源代码中以橙色代码添加
A*算法
search算法的一种变种,比扩展每个节点更高效。这种算法使用了heuristic()走最短的路径,得出来的值小于,或者最好等于真实距离:
h(x,y) ≤ actual goal distance from x,y;
这也意味着heuristic()不精确;heuristic()如下图所示,它能指导search:

在这里,仍然有open列表,但在这个列表里的元素除了g,还有g加上heuristic()的值h(x,y),用f调用:
f = g + h(x,y)
每次移除f最小的节点,这有一个例子过程,最终确定了一条最短路径:


完成A*算法,-1表示障碍物和未扩展的节点。

已在源代码中用紫色代码添加
在上面粒子中少访问的格子可能微不足道,但当数据非常庞大时就有巨大的不同,特别是出现一个非常深的死胡同效率区别就非常明显
在这个模型中障碍物会随着车辆的移动被传感器感知而扩展,A*树规划的路径会时刻更新不断取消之前的A*树,每一次重新规划的时间都在10微秒之内, 完成这个跟完成A*的区别是是否能完成它的 运动模型,去转向和直走,最明显的区别是能否能沿原轨迹返回。

动态规划
这是路径规划可选择的模型之一,给它一个map和一个或更多目的地,它能返回到任意位置的最佳路径,最重要的是它的起始位置可以是任意!
policy是一个函数将空白小格遍历变成动作,给一个这样的图和一个目的地,就能输出带路标的格子

 这样图片就包含了到达任意位置的步数
这样图片就包含了到达任意位置的步数
完成这样的编程,给一个地图,1代表障碍,0代表空位;函数能计算到每一格的最短步数值,并且返回包含这些值的表,障碍用99表示(足够大不会混淆步数)
def compute_value(): value = [[99 for row in range(len(grid[0]))] for col in range(len(grid))] change = True #标志change在有实际updata时置True,循环中置False while change: change = False for x in range(len(grid)): for y in range(len(grid[0])): if goal[0] == x and goal[1] == y: #如果出发点就是目标点,并考虑到意外目标值非0便置0,change置True表示updata if value[x][y] > 0: value[x][y] = 0
policy[x][y] = ‘*’ change = True elif grid[x][y] == 0: #出发点不是目标点情况, for a in range(len(delta)): x2 = x + delta[a][0] y2 = y + delta[a][1] if x2 >= 0 and x2 < len(grid) and y2 >=0 and y2 < len(grid[0]): #如果赋了动作的x,y还在大网格内(在空格子里并非障碍物) v2 = value[x2][y2] + cost_step #加一个成本 if v2 < value[x][y]: #取值更小的路径,updata change = True value[x][y] = v2
policy[x][y] = delta_name[a]
#以下是policy打印代码
for i in range(len(value)):
print policy[i]
事实证明,通过动态规划找到最佳解决方案比A *更容易。将上述的表格转换成动作表,修改已用梅色添加
now do something fun!将动态规划应用于现实:3D的状态空间,每个小格是2D,添加一个方向维度
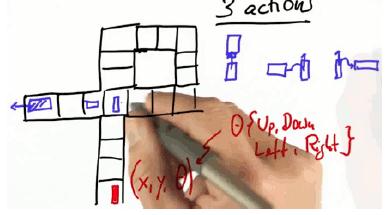
grid =[[1, 1, 1, 0, 0, 0], [1, 1, 1, 0, 1, 0], [0, 0, 0, 0, 0, 0], [1, 1, 1, 0, 1, 1], [1, 1, 1, 0, 1, 1]] forward = [[ 1, 0], # up [ 0, 1], # left [ 1, 0], # down [ 0, 1]] # right goal = [2, 0] #从左上角算起 init = [4, 3, 0] cost = [2, 1, 20] # 为cost赋三个值:右转,不转,左转 action = [1, 0, 1] action_name = ['R', '#', 'L'] def optimum_policy2D(): value = [[[999 for row in range(len(grid[0]))] for col inrange(len(grid))], [[999 for row in range(len(grid[0]))] for col in range(len(grid))], [[999 for row in range(len(grid[0]))] for col in range(len(grid))], [[999 for row in range(len(grid[0]))] for col in range(len(grid))]] policy = [[[' ' for row in range(len(grid[0]))] for col in range(len(grid))], [[' ' for row in range(len(grid[0]))] for col in range(len(grid))], [[' ' for row in range(len(grid[0]))] for col in range(len(grid))]
[[' ' for row in range(len(grid[0]))] for col in range(len(grid))]] policy2D = [[' ' for row in range(len(grid[0]))] for col in range(len(grid))] #这是最后要打印的 change = True while change: change = False #遍历所有小格并且计算值 for x in range(len(grid)): #起点是目的地 for y in range(len(grid[0])): for orientation in range(4): if goal[0] == x and goal[1] == y: if value[orientation][x][y] > 0: value[orientation][x][y] = 0 policy[orientation][x][y] = '*' change = True elif grid[x][y] == 0: #以空格开始 for i in range(3):#计算三种方法来传播值 o2 = (orientation + action[i]) % 4 #添加方向累加,取模4确保方向在3内,做一个缓冲区 x2 = x + forward[o2][0] y2 = y + forward[o2][1] if x2 >= 0 and x2 < len(grid) and y2 >= 0 and y2 < len(grid[0]) and grid[x2][y2] == 0: v2 = value[o2][x2][y2] + cost[i] if v2 < value[orientation][x][y]: #留下最小值 change = True value[orientation][x][y] = v2 policy[orientation][x][y]= action_name[i] #赋值动作标号 x = init[0] y = init[1] orientation = init[2] #这里方向是0 policy2D[x][y] = policy[orientation][x][y] #从3D表上copy到2D上来 while policy[orientation][x][y] != '*':#在没到目的地的情况下检查方向,并将方向代表的数字赋给o2 if policy[orientation][x][y] == '#': o2 = orientation elif policy[orientation][x][y] == 'R': o2 = (orientation - 1) % 4 elif policy[orientation][x][y] == 'L': o2 = (orientation + 1) % 4 x = x + forward[o2][0] #更新x、y、orientation y = y + forward[o2][1] orientation = o2 policy2D[x][y] = policy[orientation][x][y] #刚才那句赋的是起点,这里是剩下的全部 return policy2D
SIMULATION
程序能通过改变 cost functions 高效地驾驶这辆车
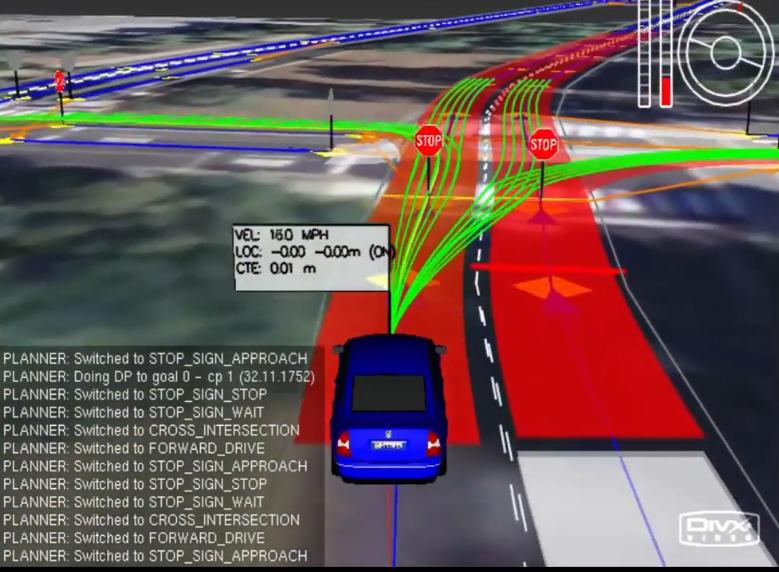
class世界是离散的,2个规划算法 - A *,它使用heuristic() 来找到one path和dynamic programming,找到一个完整的策略(policy),即为每个位置制定一个规划。不仅完成这两,还在3D世界做了动态规划。
so far,需了解如何将其转化为实际的机器人动作。 了解连续状态空间以及用来使机器人移动的所谓“控制”。
>>>next...



 浙公网安备 33010602011771号
浙公网安备 33010602011771号