Ng第十二课:支持向量机(Support Vector Machines)(三)
11 SMO优化算法(Sequential minimal optimization)
SMO算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算法,特别针对线性SVM和数据稀疏时性能更优。关于SMO最好的资料就是他本人写的《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》。
首先回到前面一直悬而未解的问题,对偶函数最后的优化问题:
要解决的是在参数![]() 上求最大值W的问题,至于
上求最大值W的问题,至于![]() 和
和![]() 都是已知数。C由我们预先设定,也是已知数。
都是已知数。C由我们预先设定,也是已知数。
按照坐标上升的思路,首先固定除![]() 以外的所有参数,然后在
以外的所有参数,然后在![]() 上求极值。等一下,这个思路有问题,因为如果固定
上求极值。等一下,这个思路有问题,因为如果固定![]() 以外的所有参数,那么
以外的所有参数,那么![]() 将不再是变量(最大值W确定其他所有值也确定)。因为问题中规定了
将不再是变量(最大值W确定其他所有值也确定)。因为问题中规定了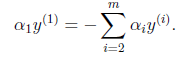 (如果其他值是定量那么a1y(1)出来的结果也是定量)
(如果其他值是定量那么a1y(1)出来的结果也是定量)
因此,需要一次选取两个参数做优化,比如![]() 和
和![]() ,此时
,此时![]() 可以由
可以由![]() 和其他参数表示出来。这样回带到W中,W就只是关于
和其他参数表示出来。这样回带到W中,W就只是关于![]() 的函数了,可解。
的函数了,可解。
这样,SMO的主要步骤如下:
意思是,第一步选取一对![]() 和
和![]() ,选取方法使用启发式方法(后面讲)。第二步,固定除
,选取方法使用启发式方法(后面讲)。第二步,固定除![]() 和
和![]() 之外的其他参数,确定W极值条件下的
之外的其他参数,确定W极值条件下的![]() ,
,![]() 由
由![]() 表示。
表示。
SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效。
下面讨论具体方法:
假设我们选取了初始值![]() 满足了问题中的约束条件(用了启发式方法)。接下来,住固定
满足了问题中的约束条件(用了启发式方法)。接下来,住固定![]() ,这样W就是
,这样W就是![]() 和
和![]() 的函数。并且
的函数。并且![]() 和
和![]() 满足条件:
满足条件:
由于![]() 都是已知固定值,因此为了方面,可将等式右边标记成实数值
都是已知固定值,因此为了方面,可将等式右边标记成实数值![]() 。
。
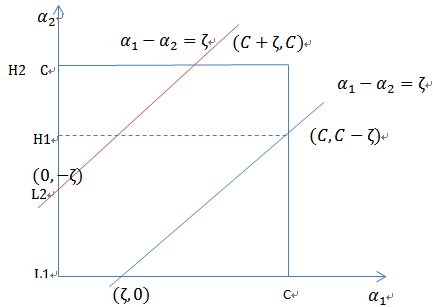
当![]() 和
和![]() 异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
异号时,也就是一个为1,一个为-1时,他们可以表示成一条直线,斜率为1。如下图:
然后反代入W中,得
展开后W可以表示成![]() 。其中a,b,c是固定值。这样,通过对W进行求导可以得到
。其中a,b,c是固定值。这样,通过对W进行求导可以得到![]() ,然而要保证
,然而要保证![]() 满足
满足![]() ,我们使用
,我们使用![]() 表示求导求出来的
表示求导求出来的![]() ,然而最后的
,然而最后的![]() ,要根据下面情况得到:
,要根据下面情况得到:
12 SMO中拉格朗日乘子的启发式选择方法
所谓的启发式选择方法主要思想是每次选择拉格朗日乘子的时候,优先选择样本前面系数![]() 的
的![]() 作优化,因为在界上(
作优化,因为在界上(![]() 为0或C)的样例对应的系数
为0或C)的样例对应的系数![]() 一般不会更改。
一般不会更改。
这条启发式搜索方法是选择第一个拉格朗日乘子用的,比如前面的![]() 。那么这样选择的话,是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个
。那么这样选择的话,是否最后会收敛。可幸的是Osuna定理告诉我们只要选择出来的两个![]() 中有一个违背了KKT条件,那么目标函数在一步迭代后值会减小。违背KKT条件不代表
中有一个违背了KKT条件,那么目标函数在一步迭代后值会减小。违背KKT条件不代表![]() ,在界上也有可能会违背。是的,因此在给定初始值
,在界上也有可能会违背。是的,因此在给定初始值![]() =0后,先对所有样例进行循环,循环中碰到违背KKT条件的(不管界上还是界内)都进行迭代更新。等这轮过后,如果没有收敛,第二轮就只针对
=0后,先对所有样例进行循环,循环中碰到违背KKT条件的(不管界上还是界内)都进行迭代更新。等这轮过后,如果没有收敛,第二轮就只针对![]() 的样例进行迭代更新。
的样例进行迭代更新。
在第一个乘子选择后,第二个乘子也使用启发式方法选择,第二个乘子的迭代步长大致正比于![]() ,选择第二个乘子能够最大化
,选择第二个乘子能够最大化![]() 。即当
。即当![]() 为正时选择负的绝对值最大的
为正时选择负的绝对值最大的![]() ,反之,选择正值最大的
,反之,选择正值最大的![]() 。
。
最后的收敛条件是在界内(![]() )的样例都能够遵循KKT条件,且其对应的
)的样例都能够遵循KKT条件,且其对应的![]() 只在极小的范围内变动。
只在极小的范围内变动。
至于如何写具体的程序,请参考John C. Platt在论文中给出的伪代码。
13 总结
其实在应用时不需要这么多推导,直接用结论写程序即可。拉格朗日对偶的重要作用是将w的计算提前并消除w,使得优化函数变为拉格朗日乘子的单一参数优化问题。
对比这么复杂的推导过程,SVM的思想确实那么简单。它不再像logistic回归一样企图去拟合样本点(中间加了一层sigmoid函数变换),而是就在样本中去找分隔线,为了评判哪条分界线更好,引入了几何间隔最大化的目标。
之后所有的推导都是去解决目标函数的最优化上了。在解决最优化的过程中,发现了w可以由特征向量内积来表示,进而发现了核函数,仅需要调整核函数就可以将特征进行低维到高维的变换,在低维上进行计算,实质结果表现在高维上。由于并不是所有的样本都可分,为了保证SVM的通用性,进行了软间隔的处理,导致的结果就是将优化问题变得更加复杂,然而惊奇的是松弛变量没有出现在最后的目标函数中。最后的优化求解问题,也被拉格朗日对偶和SMO算法化解,使SVM趋向于完美。

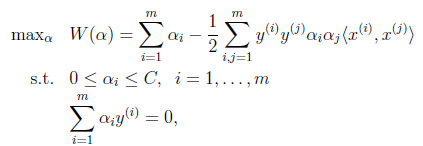

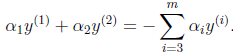
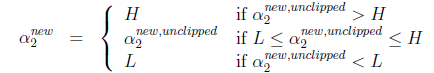


 浙公网安备 33010602011771号
浙公网安备 33010602011771号