Ng第五课：Octave 教程(Octave Tutorial)
5.1 基本操作
5.2 对数据进行灵活操作
5.3 计算数据
5.4 数据可视化
5.5 控制语句和函数
5.6 矢量化
官网安装：Installation
在线文档：http://www.gnu.org/software/octave/doc/interpreter/
5.1 基本操作
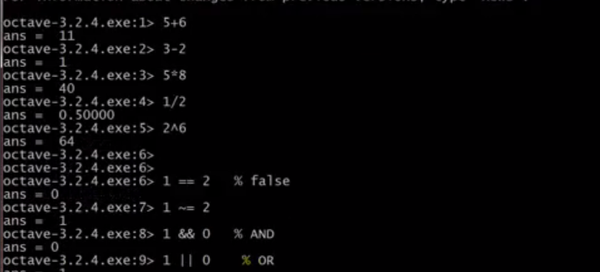
算术运算，逻辑运算 #%用于注释
ps1('>> ');可以改变提示符的样子 #注意分号
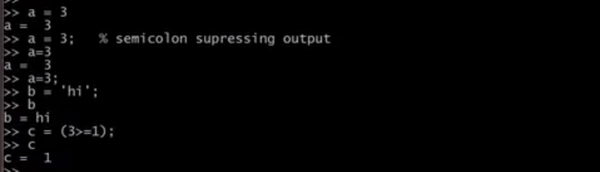
变量赋值 #加上分号后不直接打印出来，不加分号可以直接打印出来
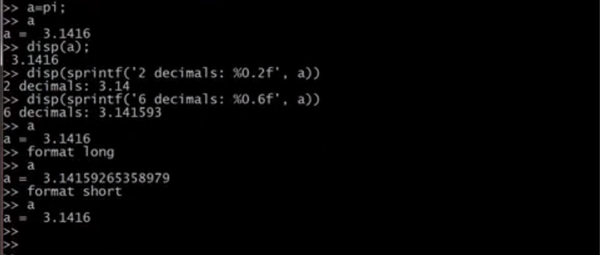
disp()和sprintf()用于打印显示变量，两者可结合使用格式输出。format可以使接下来打印的结果格式发生改变。
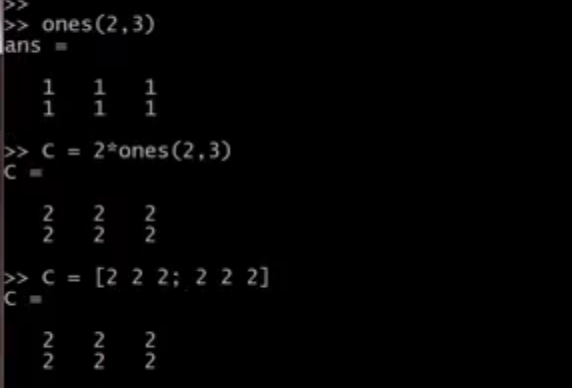
创建矩阵或向量
第一个例子是创建列向量
第二三个例子是有无步长创建横向量
创建全为1、全为0的矩阵，创建随机数矩阵
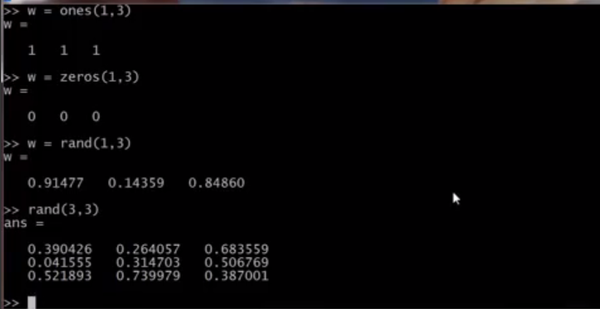
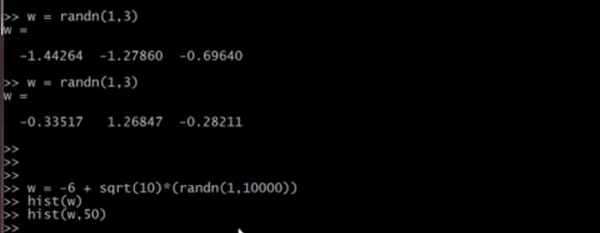
hist是用直方图形式显示各范围元素的个数，如：
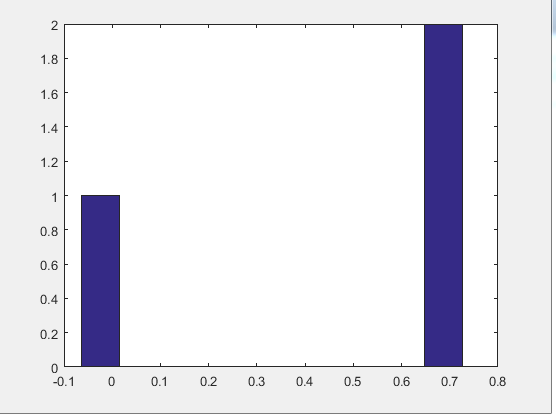
用hist显示为，其中hist(w,a)，a表示把直方图分为a份。
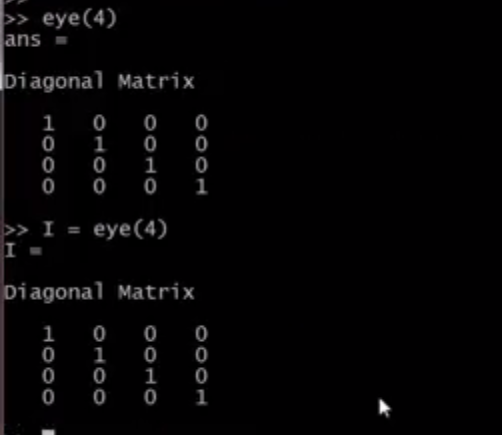
创建单位矩阵
5.2对数据进行灵活操作
——数据的各种可能的操作方式
计算矩阵维度、第一个维度、第二个维度，最大维度：
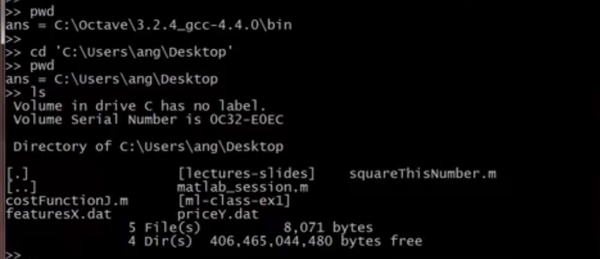
pwd显示当前工作目录，cd '.....'切换工作目录，ls列出当前目录中文件
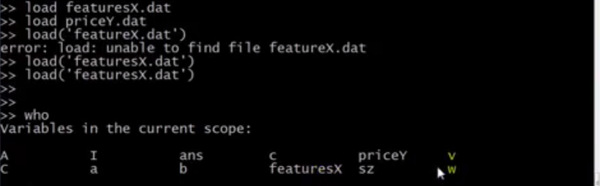
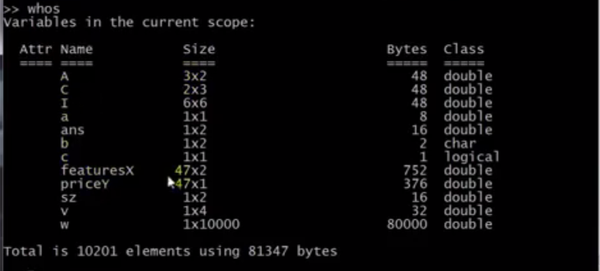
加载文件、查看变量、查看详细变量信息 #load X和load('X')的作用一致
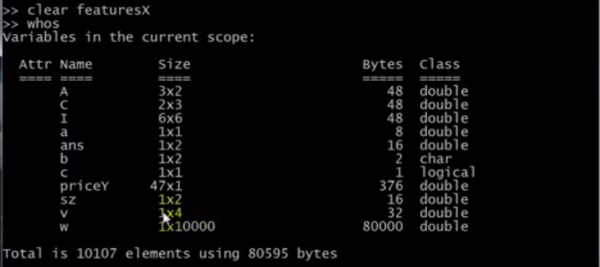
clear删除所有的变量，clear变量名删除某一个变量
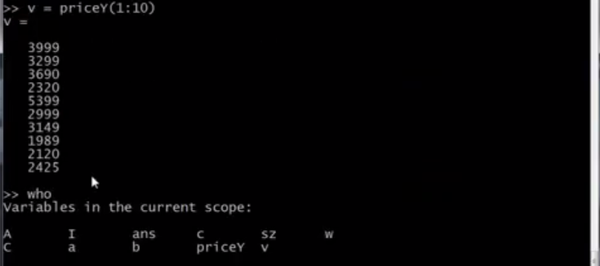
priceY(m:n)表示取向量的第m个元素到第n个元素进行赋值 #对于矩阵来说，元素编号是从上到下，从左向右依次编号
将矩阵数据存储到文件中，保存为文本格式，.dat格式也可以
对矩阵进行切片索引和拓展
奇特的将第一和三行的所有元素进行切片显示
创建后的赋值方式
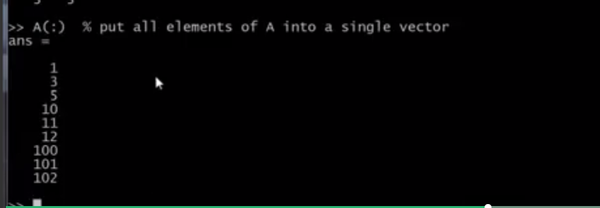
将矩阵所有元素依次放入一个向量中
组合矩阵
5.3数据运算
A*C：A与C矩阵正常相乘
A .* B：两个矩阵中的每个对应位置的元素相乘
A .^ 2：对矩阵每个元素进行平方
1./A：对A的每个元素进行除法，这里是每个元素取倒
log(A)：以e为底，对每个元素求log
exp(A)：以e的A中每个元素为幂的结果
abs(A)：对A的每个元素求绝对值
-A：对A的每个元素求负数
v+1：对v中每个元素都加1
A‘：矩阵A的转置
pinv()：求矩阵逆
max(v)：向量v中最大的元素，矩阵的含义有点不同，得到包含了来自各列的最大元素组成的行向量
A<3：对每个元素都进行比较，得到的结果为1或者0
find(A<3)：得到一个向量，列出相应小于3的元素的索引
magic(n)：生成nxn的矩阵，每行每列每个对角线得到的和相同
sum：将矩阵所有元素进行相加
prod：将数组元素全部相乘，如果是矩阵，则是对每一列看作向量进行相乘，得到向量
floor：对每个元素向下取整
ceil：对每个元素向上取整
5.4 数据可视化
对变量t进行赋值，构造正弦函数，然后作图：
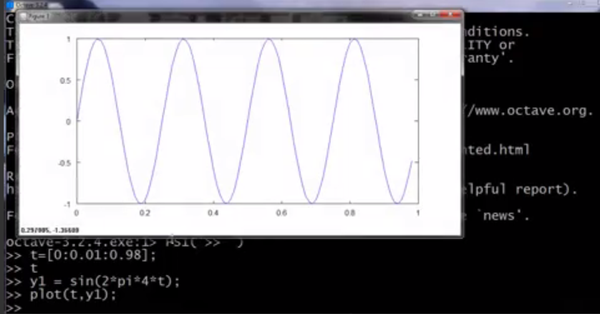
xlabel对x轴命名，legend对每条线进行说明，title追加名字，print保存图像到本地
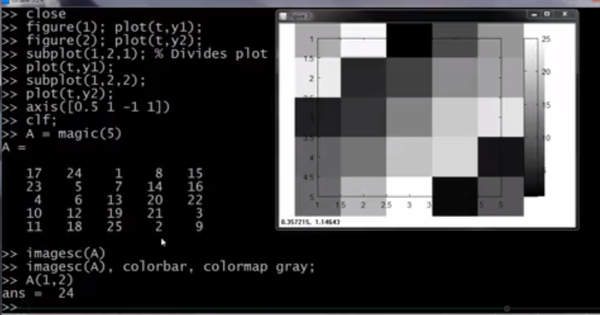
代码第1行关闭图像，23行对图像命名，4567行将一张图分为两部分呈现第1部分，第8行分别设置x轴和y轴的范围，clf清除现有图像中的内容
之后是用imagesc对矩阵进行可视化
5.5 控制语句和函数
for循环语句的例子
while循环例子 #习惯于循环后打逗号，代码有缩进便于阅读，用end表示代码的结束，分号和写c相似
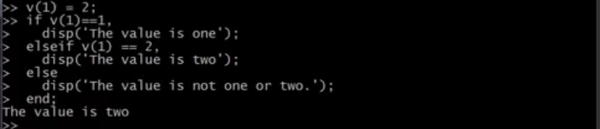
if语句的例子，和c完全一致 #使用quit或者exit可以使matlab退出
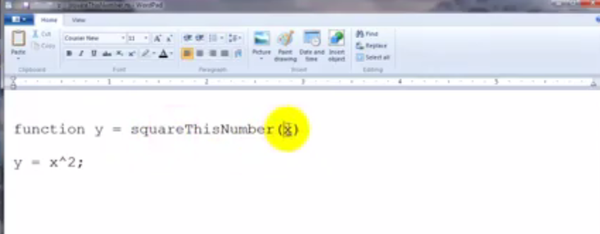
用wordpad自定义一个函数
切换到路径下，或者用addpath加入搜索路径，可以使用自定义函数。
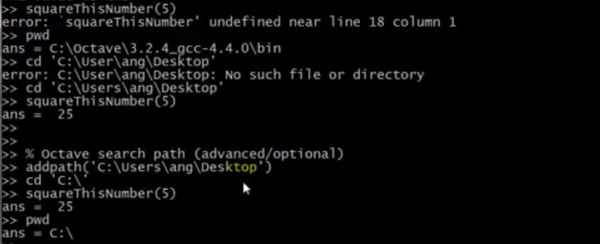
注：自定义函数的用法，必须创建.m文件，且文件名和函数名称必须一致。
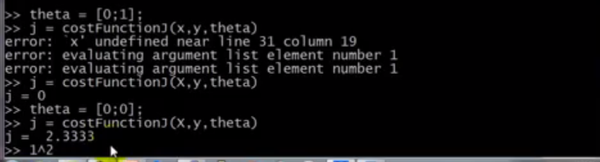
EXP下面举个计算成本函数的例子，有这样一个数据集合，计算他的成本函数
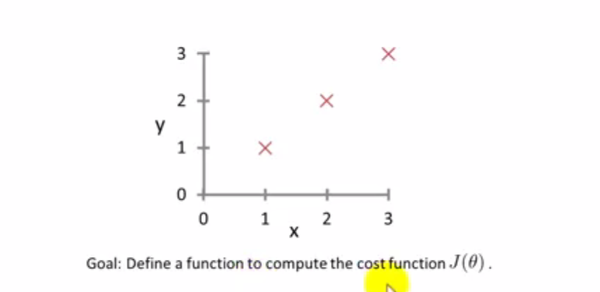
首先输入数据集合
然后输入自定义函数
直接计算结果
5.6 向量化
本节讲解如何使用计算机和软件自带的库来加速运算。将大量数据向量化，使用矩阵工具进行运算，可以借助机器大大加快处理速度。
EXP举一个数据向量化的例子，对于图中的运算，可以抽象为两个向量。如果不用矩阵，直接运算的话，程序如下图左所示。用矩阵则如图右所示，更简单。
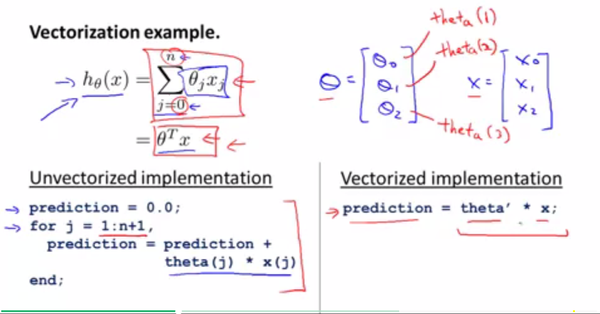
以上图中的运算为例子，如何快速的同步运算thelta，如何向量化，加速运算
分解成各部分然后变成向量
