线头 DP
对于一种需要通过相邻两项来维护的一些 DP 问题,通常的 DP 会无法转移。这时便要使用线头 DP。这种 DP 又名连续段 DP,其关键在于维护已近满足条件的不同连续段的贡献总和。
就从例题来说吧。
P6758 [BalticOI 2013] Vim
首先 e 的贡献可以提前算,为 \(2cnt_e\)(向左走和删除)。然后可以把序列中所有的 e 去掉,对新串做操作。
唯一不同的是每个 e 之后的非 e 都必须经过,我们把他们称作关键点。
然后我们通过画图发现如果把 \((i, i + 1)\) 看成一个小线段,那么每一个小线段被覆盖的次数一定为 \(1\) 或 \(3\)(最后一段除外,因为可能删完了就不往后跳了)。
设计 DP:\(f_{i, j}\) 表示第 \(i\) 段被覆盖一次,且覆盖这一段的跳跃终点字符是 \(j\) 的答案;\(g_{i, j, k}\) 表示第 \(i\) 段被覆盖三次,且第一次和第三次覆盖这一段的跳跃的终点字符分别是 \(j\) 和 \(k\) 的答案。
转移的话考虑分类讨论覆盖第 \(i - 1\) 段的情况,加上多出来的贡献即可。转移就不列举了。
总复杂度 \(O(n V^2)\)。\(V = 10\) 是值域。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define ll long long
using namespace std;
const int N = 7e4 + 5; const ll INF = (ll)1e18 + 5;
int n, len, ans, a[N], flag[N]; ll f[N][10], g[N][10][10]; char c;
inline void chkmin(ll & x, ll y) { x = x < y ? x : y; }
int main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n; int tmp = 1;
_for (i, 1, n) {
cin >> c;
if (c != 'e') a[ ++ len] = c - 'a', flag[len] = tmp, tmp = 0;
else ans ++ , tmp = 1;
} n = len;
_for (i, 0, n) _for (j, 0, 9) {
f[i][j] = INF;
_for (k, 0, 9) g[i][j][k] = INF;
} f[0][a[1]] = 0;
_for (i, 1, n) _for (j, 0, 9) {
ll & F = f[i][j];
if ( ! flag[i] && j ^ a[i]) chkmin(F, f[i - 1][j]); chkmin(F, f[i - 1][a[i]] + 2);
if (j ^ a[i]) chkmin(F, g[i - 1][a[i]][j]); chkmin(F, g[i - 1][a[i]][a[i]] + 2);
_for (k, 0, 9) {
ll & G = g[i][j][k];
if (j ^ a[i] && k ^ a[i]) chkmin(G, g[i - 1][j][k] + 1);
if (j ^ a[i]) chkmin(G, g[i - 1][j][a[i]] + 3);
if (k ^ a[i]) chkmin(G, g[i - 1][a[i]][k] + 3); chkmin(G, g[i - 1][a[i]][a[i]] + 5), chkmin(G, f[i - 1][a[i]] + 5);
if (j ^ a[i]) chkmin(G, f[i - 1][j] + 3);
}
} cout << ans * 2 + f[n][4] - 2 << "\n";
return 0;
}
P5999 [CEOI 2016] kangaroo
先转化成:求有多少种排列,使得 \(\forall 1 < i < n\),都满足 \(\max(p_{i - 1}, p_{i + 1}) < p_i\) 或 \(p_i < \min(p_{i - 1}, p_{i + 1})\),且 \(p_1 = S, p_n = T\)。
设 \(f_{i, j}\) 表示目前插入了 \([1, i]\),开了 \(j\) 段的方案数。考虑从小到大往排列中加数:
-
如果 \(i \neq S\) 且 \(i \neq T\):
-
新开一段:进行这一步之前有 \(j - 1\) 段,一共 \(j\) 个空可以插入。但如果 \(i > S\),则不能插入 \(S\) 前面。\(T\) 同理。所以 \(f_{i, j} \leftarrow (j - [i > S] - [i > T]) \times f_{i - 1, j - 1}\)。
-
放在一段之前或之后:这样会导致 \(i\) 左右两边一个比他大,一个比他小,不满足条件。
-
合并两段:这一步之前有 \(j\) 段,一共 \(j - 1\) 个空可以插入。所以 \(f_{i, j} \leftarrow j \times f_{i - 1, j + 1}\)。
-
-
如果 \(i = S\) 或 \(i = T\):\(f_{i, j} \leftarrow f_{i - 1, j - 1} + f_{i - 1, j}\)。
答案即为 \(f_{n, 1}\)。
但你会发现这个 DP 很奇怪。有可能会出现你两个段之间间隔只有 \(1\),但是新开一段的时候会将这个间隔拿来转移,这样会错误。但其实不会,因为 DP 状态没有规定每个段的位置。对于一些情况,我们总是能排出一种段的“摆放方式”使得合法。如果无法排出,该状态一定不会对答案造成影响。所以这个 DP 是对的。
复杂度 \(O(n^2)\)。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
using namespace std;
const int N = 2005, P = 1e9 + 7;
int n, S, T, f[N][N];
inline int mul(int x, int y) { return 1ll * x * y % P; }
inline void Add(int & x, int y) { x = x + y >= P ? x + y - P : x + y; }
int main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> S >> T, f[0][0] = 1;
_for (i, 1, n) _for (j, 1, i) {
if (i ^ S && i ^ T) Add(f[i][j], mul(j - (i > S) - (i > T), f[i - 1][j - 1])), Add(f[i][j], mul(j, f[i - 1][j + 1]));
else Add(f[i][j], f[i - 1][j] + f[i - 1][j - 1]);
} cout << f[n][1] << "\n";
return 0;
}
P9197 [JOI Open 2016] 摩天大楼
按照 \(a\) 从大到小插入。值域上每减一,题目要求的差的绝对值之和都会增加段数 $ \times 2$(左右边界除外):
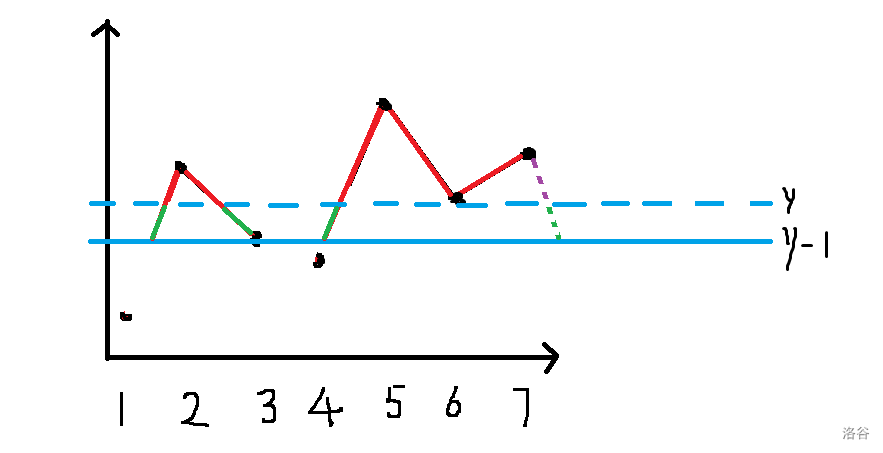
定义状态 \(f_{i, j, k, 0 / 1, 0 / 1}\) 表示 决策了前 \(i\) 大的数字,目前有 \(j\) 段,和为 \(k\),左边和右边有 / 没有放数 的方案数。
转移类似上一道题,不赘述了。时空复杂度 \(O(n^2 L)\)。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define F f[i - 1][j][k][x][y]
using namespace std;
const int N = 105, M = 1005, P = 1e9 + 7;
int n, L, ans, a[N], f[N][N][M][2][2]; // cur at i, j segments, sum is k, 0/1 on the left and right
inline int mul(int x, int y) { return 1ll * x * y % P; }
inline void Add(int & x, int y) { x = x + y >= P ? x + y - P : x + y; }
int main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> L, f[1][1][0][0][0] = f[1][1][0][0][1] = f[1][1][0][1][0] = 1;
_for (i, 1, n) cin >> a[i]; sort(a + 1, a + n + 1, greater<int> ());
if (n == 1) return cout << "1\n", 0; int nk;
_for (i, 2, n) _for (j, 1, i - 1) _for (k, 0, L) _for (x, 0, 1) _for (y, 0, 1) {
nk = k + (j * 2 - x - y) * (a[i - 1] - a[i]);
if (nk > L) continue;
if (j > 1) Add(f[i][j + 1][nk][x][y], mul(j - 1, F)); // form a new segment (add in the middle)
if ( ! x) Add(f[i][j + 1][nk][0][y], F), Add(f[i][j + 1][nk][1][y], F); // form a new segment (add on the left)
if ( ! y) Add(f[i][j + 1][nk][x][0], F), Add(f[i][j + 1][nk][x][1], F); // form a new segment (add on the right)
if (j > 1) Add(f[i][j][nk][x][y], mul(2 * (j - 1), F)); // add to the side of one segment (add in the middle)
if ( ! x) Add(f[i][j][nk][0][y], F), Add(f[i][j][nk][1][y], F); // add to the side of one segment (add on the left)
if ( ! y) Add(f[i][j][nk][x][0], F), Add(f[i][j][nk][x][1], F); // add to the side of one segment (add on the right)
if (j > 1) Add(f[i][j - 1][nk][x][y], mul(j - 1, F)); // merge two segments
} _for (i, 0, L) Add(ans, f[n][1][i][1][1]); cout << ans << "\n";
return 0;
}
P7967 [COCI 2021/2022 #2] Magneti
考虑两个磁铁是否相互作用,显然只需考虑半径更大的磁铁。
按照半径从小到大排序依次加入。我们尽量让加入的磁铁尽量紧贴,假设求出来的磁铁覆盖的长度为 \(x\),那么根据组合数容易得到对答案的贡献为 \(\binom{L - x + n}{n}\)。
DP 设 \(f_{i, j, k}\) 表示当前已经加入了 \(i\) 个磁铁,有 \(j\) 段,覆盖的总长度为 \(k\) 的方案数。转移同上面的题目。
唯一需要注意的是这个题的状态没有关心各个段的顺序,所以转移系数要特殊处理一下。
复杂度 \(O(n^2L)\)。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define F f[i][j][k]
using namespace std;
const int N = 55, M = 1e4 + N, P = 1e9 + 7;
int n, m, ans, a[N], fac[M], ifac[M], f[N][N][M];
inline int mul(int x, int y) { return 1ll * x * y % P; }
inline void Add(int & x, int y) { x = x + y >= P ? x + y - P : x + y; }
inline void Mul(int & x, int y) { x = 1ll * x * y % P; }
inline int Pow(int x, int y) {
int res = 1;
for ( ; y; y >>= 1, Mul(x, x)) if (y & 1) Mul(res, x); return res;
} inline int binom(int x, int y) { return x >= y ? mul(fac[x], mul(ifac[y], ifac[x - y])) : 0; }
int main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m, f[0][0][0] = fac[0] = ifac[0] = 1;
_for (i, 1, M - 1) fac[i] = mul(fac[i - 1], i), ifac[i] = Pow(fac[i], P - 2);
_for (i, 1, n) cin >> a[i]; sort(a + 1, a + n + 1);
_for (i, 1, n) _for (j, 1, i) _for (k, 0, m) {
if (k) Add(F, f[i - 1][j - 1][k - 1]);
if (k >= a[i]) Add(F, mul(2 * j, f[i - 1][j][k - a[i]]));
if (k >= 2 * a[i] - 1) Add(F, mul(mul(j, j + 1), f[i - 1][j + 1][k - (2 * a[i] - 1)]));
} _for (i, 0, m) Add(ans, mul(f[n][1][i], binom(m - i + n, n))); cout << ans << "\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号