机器学习实战8-Apriori算法
1. 用途和原理
1.1 用途
用于关联分析,即在大规模数据中寻找有趣的关系,有两种形式:频繁项集和关联规则。频繁项集:指经常出现在一块的物品集合。关联规则:暗示两种物品之间可能存在很强的关系。典型一个案例便是:尿布与啤酒(感兴趣可以了解一下)。
1.2 原理
Apriori原理:如果某个项集是频繁的那么它的所有子集也是频繁的。反过来,如果某个项集非频繁,那么其所有的超集也非频繁。如下图,阴影部分 [2,3] 以及其超集均为为非频繁集。

两个概念:
支持度:一个项集的支持度定义为数据集中包含该项集的记录所占的比例。
可信度:针对关联规则所定义,如规则 A->B(可简单理解为 A 导致 B ),则该规则可信度=支持度{A,B}/支持度{A}
1.3 算法过程
-
收集数据
-
找出满足阈值条件的频繁项集
-
运用关联规则找出物品间关系
2. Python实现
2.1 构建频繁项集
伪代码如下:
当集合中项的个数大于0时:
-
- 构建一个K个项组成的候选项集的列表
- 检查数据以确认每个项集是频繁的(即观察支持度是否大于阈值)
- 保留频繁项集并构建K+1项组成的候选项集列表
主要核心代码如下:
1 # 创建候选项集Ck 2 def aprioriGen(Lk,k): 3 retList=[] 4 lenLk=len(Lk) 5 # 将每一个集合与其他所有集合遍历配对,每两个元素检查其前k-2个值是否相同,如果相同,合并之,减小配对时间 6 for i in range(lenLk): 7 for j in range(i+1,lenLk): 8 # list[:k-2]返回的是前k-2个数 9 L1=list(Lk[i])[:k-2] 10 L2=list(Lk[j])[:k-2] 11 L1.sort() 12 L2.sort() 13 if L1==L2: 14 retList.append(Lk[i]|Lk[j]) 15 return retList 16 17 # 创建频繁项集L,及其对应的支持度 18 def apriori(dataSet,minSupport=0.5): 19 C1=creatC1(dataSet) 20 D=list(map(set,dataSet)) 21 L1,supportData=scanD(D,C1,minSupport) 22 L=[L1] 23 k=2 24 # 循环产生Lk,并放入列表中[L1,L2,.....Lk],直到Lk为空 25 while (len(L[k-2])>0): 26 Ck=aprioriGen(L[k-2],k) 27 Lk,supK=scanD(D,Ck,minSupport) 28 # 将新的集合支持度添加入支持度集合中去 29 supportData.update(supK) 30 L.append(Lk) 31 k+=1 32 return L,supportData
当我们输入一组数据时:[[1,3,4],[2,3,5],[1,2,3,5],[2,5]],观察其构建的频繁项集。
完整代码如下:

1 # 1.创建数据集 2 def loadDataSet(): 3 return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]] 4 5 # 2.构建集合C1,C1是所有种类(大小为1)的集合 6 def creatC1(dataSet): 7 C1=[] 8 for transaction in dataSet: 9 for item in transaction: 10 if not [item] in C1: 11 C1.append([item]) 12 C1.sort() 13 # 与原文比有所修改 14 return list(map(frozenset,C1)) 15 16 # 3.创建某一级频繁项集Lk 17 def scanD(D,Ck,minSupport): 18 ssCnt={} 19 for tid in D: 20 # print(tid) 21 for can in Ck: 22 # print(can) 23 # 判断tid中是否包含can 24 if can.issubset(tid): 25 # 创建字典,key是can,值是次数 26 # 与原文有所差别 27 if not can in ssCnt: 28 ssCnt[can]=1 29 else: 30 ssCnt[can]+=1 31 numItems=float(len(D)) 32 retList=[] 33 supportData={} 34 for key in ssCnt: 35 # 计算每个key支持度 36 support=ssCnt[key]/numItems 37 # 如果支持度大于最小支持度,插入种类key,并添加入到关于支持度的字典 38 if support>=minSupport: 39 retList.insert(0,key) 40 supportData[key]=support 41 return retList,supportData 42 43 # 4.创建候选项集Ck 44 def aprioriGen(Lk,k): 45 retList=[] 46 lenLk=len(Lk) 47 # 将每一个集合与其他所有集合遍历配对,每两个元素检查其前k-2个值是否相同,如果相同,合并之,减小配对时间 48 for i in range(lenLk): 49 for j in range(i+1,lenLk): 50 # list[:k-2]返回的是前k-2个数 51 L1=list(Lk[i])[:k-2] 52 L2=list(Lk[j])[:k-2] 53 L1.sort() 54 L2.sort() 55 if L1==L2: 56 retList.append(Lk[i]|Lk[j]) 57 return retList 58 59 # 5.创建频繁项集L,及其对应的支持度 60 def apriori(dataSet,minSupport=0.5): 61 C1=creatC1(dataSet) 62 D=list(map(set,dataSet)) 63 L1,supportData=scanD(D,C1,minSupport) 64 L=[L1] 65 k=2 66 # 循环产生Lk,并放入列表中[L1,L2,.....Lk],直到Lk为空 67 while (len(L[k-2])>0): 68 Ck=aprioriGen(L[k-2],k) 69 Lk,supK=scanD(D,Ck,minSupport) 70 # 将新的集合支持度添加入支持度集合中去 71 supportData.update(supK) 72 L.append(Lk) 73 k+=1 74 return L,supportData 75 76 dataSet=loadDataSet() 77 L,suppData=apriori(dataSet) 78 print(L) 79 print(suppData)

如图表达:

2.2 构建关联规则
主要用到的是分级法,可以首先从一个频繁项集开始,接着建立一个规则列表,其中规则右部只包含一个元素,测试这些规则,去掉不满足最低可信度条件的规则。接着再利用剩余的规则,合并,规则右边包含两个元素,一直往后延续。观察下面几个主要的程序更易理解。
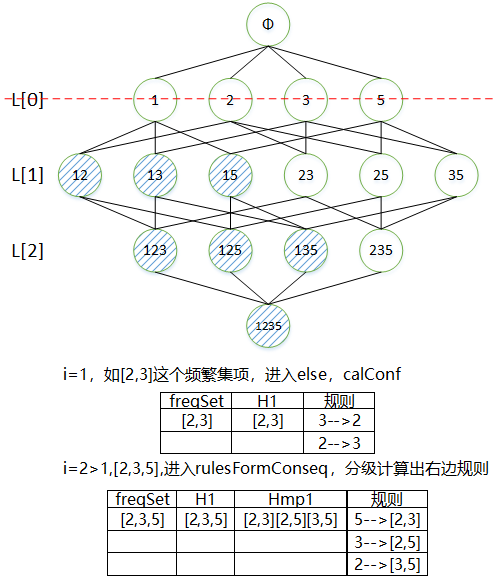
1 ''' freqSet--频繁项集 2 H--频繁项集中的所有元素 3 ''' 4 def generateRules(L,supportData,minConf=0.7): 5 bigRuleList=[] 6 for i in range(1,len(L)): 7 for freqSet in L[i]: 8 H1=[frozenset([item]) for item in freqSet] 9 if (i>1): 10 rulesFormConseq(freqSet,H1,supportData,bigRuleList,minConf) 11 else: 12 calcConf(freqSet,H1,supportData,bigRuleList,minConf) 13 return bigRuleList 14 15 # 依次计算:【(freqSet-H中的单个元素)-->H中的单个元素】的可信度 16 def calcConf(freqSet,H,supportData,br1,minConf=0.7): 17 prunedH=[] 18 for conseq in H: 19 conf=supportData[freqSet]/supportData[freqSet-conseq] 20 # 如果大于最低可信度值,规则存入br1中,记录入prunedH 21 if conf>=minConf: 22 # print(freqSet-conseq,'-->',conseq,'conf:',conf) 23 br1.append((freqSet-conseq,conseq,conf)) 24 prunedH.append(conseq) 25 return prunedH 26 27 # 建立某频繁集项的所有满足阈值条件的规则 28 def rulesFormConseq(freqSet,H,supportData,br1,minConf=0.7): 29 m=len(H[0]) 30 # 分级法:右边是规则列表,从一个规则到两个规则到三个规则...... 31 # 此处的 m+1 条件保证的是:创建最后一层级的规则不会使用所有频繁集项中的元素,即左边不会为空至少保证一个元素 32 if (len(freqSet)>(m+1)): 33 Hmp1=aprioriGen(H,m+1) 34 Hmp1=calcConf(freqSet,Hmp1,supportData,br1,minConf) 35 if (len(Hmp1)>1): 36 rulesFormConseq(freqSet,Hmp1,supportData,br1,minConf)
接着2.1中内容,找出关联规则,完整程序如下:

1 # 1.创建数据集 2 def loadDataSet(): 3 return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]] 4 5 # 2.构建集合C1,C1是所有种类(大小为1)的集合 6 def creatC1(dataSet): 7 C1=[] 8 for transaction in dataSet: 9 for item in transaction: 10 if not [item] in C1: 11 C1.append([item]) 12 C1.sort() 13 # 与原文比有所修改 14 return list(map(frozenset,C1)) 15 16 # 3.创建某一级频繁项集Lk 17 def scanD(D,Ck,minSupport): 18 ssCnt={} 19 for tid in D: 20 # print(tid) 21 for can in Ck: 22 # print(can) 23 # 判断tid中是否包含can 24 if can.issubset(tid): 25 # 创建字典,key是can,值是次数 26 # 与原文有所差别 27 if not can in ssCnt: 28 ssCnt[can]=1 29 else: 30 ssCnt[can]+=1 31 numItems=float(len(D)) 32 retList=[] 33 supportData={} 34 for key in ssCnt: 35 # 计算每个key支持度 36 support=ssCnt[key]/numItems 37 # 如果支持度大于最小支持度,插入种类key,并添加入到关于支持度的字典 38 if support>=minSupport: 39 retList.insert(0,key) 40 supportData[key]=support 41 return retList,supportData 42 43 # 4.创建候选项集Ck 44 def aprioriGen(Lk,k): 45 retList=[] 46 lenLk=len(Lk) 47 # 将每一个集合与其他所有集合遍历配对,每两个元素检查其前k-2个值是否相同,如果相同,合并之,减小配对时间 48 for i in range(lenLk): 49 for j in range(i+1,lenLk): 50 # list[:k-2]返回的是前k-2个数 51 L1=list(Lk[i])[:k-2] 52 L2=list(Lk[j])[:k-2] 53 L1.sort() 54 L2.sort() 55 if L1==L2: 56 retList.append(Lk[i]|Lk[j]) 57 return retList 58 59 # 5.创建频繁项集L,及其对应的支持度 60 def apriori(dataSet,minSupport=0.5): 61 C1=creatC1(dataSet) 62 D=list(map(set,dataSet)) 63 L1,supportData=scanD(D,C1,minSupport) 64 L=[L1] 65 k=2 66 # 循环产生Lk,并放入列表中[L1,L2,.....Lk],直到Lk为空 67 while (len(L[k-2])>0): 68 Ck=aprioriGen(L[k-2],k) 69 Lk,supK=scanD(D,Ck,minSupport) 70 # 将新的集合支持度添加入支持度集合中去 71 supportData.update(supK) 72 L.append(Lk) 73 k+=1 74 return L,supportData 75 76 ''' freqSet--频繁项集 77 H--频繁项集中的所有元素 78 ''' 79 def generateRules(L,supportData,minConf=0.7): 80 bigRuleList=[] 81 for i in range(1,len(L)): 82 for freqSet in L[i]: 83 H1=[frozenset([item]) for item in freqSet] 84 if (i>1): 85 rulesFormConseq(freqSet,H1,supportData,bigRuleList,minConf) 86 else: 87 calcConf(freqSet,H1,supportData,bigRuleList,minConf) 88 return bigRuleList 89 90 # 依次计算:【(freqSet-H中的单个元素)-->H中的单个元素】的可信度 91 def calcConf(freqSet,H,supportData,br1,minConf=0.7): 92 prunedH=[] 93 for conseq in H: 94 conf=supportData[freqSet]/supportData[freqSet-conseq] 95 # 如果大于最低可信度值,规则存入br1中,记录入prunedH 96 if conf>=minConf: 97 # print(freqSet-conseq,'-->',conseq,'conf:',conf) 98 br1.append((freqSet-conseq,conseq,conf)) 99 prunedH.append(conseq) 100 return prunedH 101 102 # 建立某频繁集项的所有满足阈值条件的规则 103 def rulesFormConseq(freqSet,H,supportData,br1,minConf=0.7): 104 m=len(H[0]) 105 # 分级法:右边是规则列表,从一个规则到两个规则到三个规则...... 106 # 此处的 m+1 条件保证的是:创建最后一层级的规则不会使用所有频繁集项中的元素,即左边不会为空至少保证一个元素 107 if (len(freqSet)>(m+1)): 108 Hmp1=aprioriGen(H,m+1) 109 Hmp1=calcConf(freqSet,Hmp1,supportData,br1,minConf) 110 if (len(Hmp1)>1): 111 rulesFormConseq(freqSet,Hmp1,supportData,br1,minConf) 112 113 dataSet=loadDataSet() 114 L,suppData=apriori(dataSet) 115 rules=generateRules(L,suppData,minConf=0.5) 116 print(L) 117 print(suppData) 118 print(rules)

3.示例:毒蘑菇
完整程序:
1 # 1.创建数据集 2 def loadDataSet(): 3 return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]] 4 5 # 2.构建集合C1,C1是所有种类(大小为1)的集合 6 def creatC1(dataSet): 7 C1=[] 8 for transaction in dataSet: 9 for item in transaction: 10 if not [item] in C1: 11 C1.append([item]) 12 C1.sort() 13 # 与原文比有所修改 14 return list(map(frozenset,C1)) 15 16 # 3.创建某一级频繁项集Lk 17 def scanD(D,Ck,minSupport): 18 ssCnt={} 19 for tid in D: 20 # print(tid) 21 for can in Ck: 22 # print(can) 23 # 判断tid中是否包含can 24 if can.issubset(tid): 25 # 创建字典,key是can,值是次数 26 # 与原文有所差别 27 if not can in ssCnt: 28 ssCnt[can]=1 29 else: 30 ssCnt[can]+=1 31 numItems=float(len(D)) 32 retList=[] 33 supportData={} 34 for key in ssCnt: 35 # 计算每个key支持度 36 support=ssCnt[key]/numItems 37 # 如果支持度大于最小支持度,插入种类key,并添加入到关于支持度的字典 38 if support>=minSupport: 39 retList.insert(0,key) 40 supportData[key]=support 41 return retList,supportData 42 43 # 4.创建候选项集Ck 44 def aprioriGen(Lk,k): 45 retList=[] 46 lenLk=len(Lk) 47 # 将每一个集合与其他所有集合遍历配对,每两个元素检查其前k-2个值是否相同,如果相同,合并之,减小配对时间 48 for i in range(lenLk): 49 for j in range(i+1,lenLk): 50 # list[:k-2]返回的是前k-2个数 51 L1=list(Lk[i])[:k-2] 52 L2=list(Lk[j])[:k-2] 53 L1.sort() 54 L2.sort() 55 if L1==L2: 56 retList.append(Lk[i]|Lk[j]) 57 return retList 58 59 # 5.创建频繁项集L,及其对应的支持度 60 def apriori(dataSet,minSupport=0.5): 61 C1=creatC1(dataSet) 62 D=list(map(set,dataSet)) 63 L1,supportData=scanD(D,C1,minSupport) 64 L=[L1] 65 k=2 66 # 循环产生Lk,并放入列表中[L1,L2,.....Lk],直到Lk为空 67 while (len(L[k-2])>0): 68 Ck=aprioriGen(L[k-2],k) 69 Lk,supK=scanD(D,Ck,minSupport) 70 # 将新的集合支持度添加入支持度集合中去 71 supportData.update(supK) 72 L.append(Lk) 73 k+=1 74 return L,supportData 75 76 ''' freqSet--频繁项集 77 H--频繁项集中的所有元素 78 ''' 79 def generateRules(L,supportData,minConf=0.7): 80 bigRuleList=[] 81 for i in range(1,len(L)): 82 for freqSet in L[i]: 83 H1=[frozenset([item]) for item in freqSet] 84 if (i>1): 85 rulesFormConseq(freqSet,H1,supportData,bigRuleList,minConf) 86 else: 87 calcConf(freqSet,H1,supportData,bigRuleList,minConf) 88 return bigRuleList 89 90 # 依次计算:【(freqSet-H中的单个元素)-->H中的单个元素】的可信度 91 def calcConf(freqSet,H,supportData,br1,minConf=0.7): 92 prunedH=[] 93 for conseq in H: 94 conf=supportData[freqSet]/supportData[freqSet-conseq] 95 # 如果大于最低可信度值,规则存入br1中,记录入prunedH 96 if conf>=minConf: 97 print(freqSet-conseq,'-->',conseq,'conf:',conf) 98 br1.append((freqSet-conseq,conseq,conf)) 99 prunedH.append(conseq) 100 return prunedH 101 102 # 建立某频繁集项的所有满足阈值条件的规则 103 def rulesFormConseq(freqSet,H,supportData,br1,minConf=0.7): 104 m=len(H[0]) 105 # 分级法:右边是规则列表,从一个规则到两个规则到三个规则...... 106 # 此处的 m+1 条件保证的是:创建最后一层级的规则不会使用所有频繁集项中的元素,即左边不会为空至少保证一个元素 107 if (len(freqSet)>(m+1)): 108 Hmp1=aprioriGen(H,m+1) 109 Hmp1=calcConf(freqSet,Hmp1,supportData,br1,minConf) 110 if (len(Hmp1)>1): 111 rulesFormConseq(freqSet,Hmp1,supportData,br1,minConf) 112 113 114 mushDatSet=[line.split() for line in open('mushroom.dat').readlines()] 115 print(mushDatSet) 116 L,suppData=apriori(mushDatSet,minSupport=0.3) 117 rules=generateRules(L,suppData,minConf=0.7) 118 for item in L[3]: 119 if item.intersection('2'): 120 print(item) 121 print(rules) 122 print(L)


