机器学习实战7-树回归

　　本文源自机器学习实战，总结理解内容,书中有些部分程序有错误，下文均修改过，建议自己手撕一遍，理解起来很爽。

1 CART分类与回归树

  1. CART全称：Classification and Regression Trees，即分类回归树

  2. 之前学到决策树，用的是ID3算法，做的是分类运动，这里的CART算法既可以做分类也可以做回归，本文用到的是回归。

  3. ID3决策树处理的是特征为离散值的特征（如瓜的颜色：黑、红、绿等等啊），此处的CART可以处理连续的特征值（如某特征：0.2、0.56、1.89等等）

  4. CART是一个二叉树，大于节点特征值的放入左侧树，小于节点特征值的放入右侧（当然如果你喜欢可以反着放）

  5. 特征值选取：

    1. 当做回归时：特征值选取依照的是最小二乘法，计算误差平方和

    2. 当作分类时：特征值选取依照的则是基尼系数，具体表示百度可搜一堆

  6. CART回归树过程大致如下：

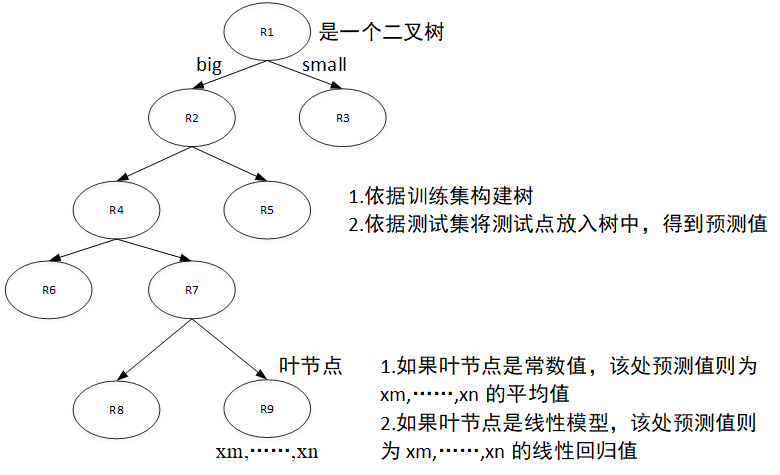
2 CART回归

2.1 算法流程：

  1. 输入训练集D

  2. 递归的将每个区域划分每个子区域的输出值，构建二叉决策树

    1. 选择最优切分量、与切分点（分成两份，计算最小误差的的状态）

    2. 决定相应区域的输出值

    3. 循环以上直至满足停止条件

  3. 得到树

　　代码：

 1 from numpy import *
 2 import matplotlib.pyplot as plt
 3 
 4 # 1.导入数据
 5 def loadDataSet(fileName):
 6     dataMat=[]
 7     fr=open(fileName)
 8     for line in fr.readlines():
 9         curLine=line.strip().split('\t')
10         # 与原文不一致
11         fltLine=list(map(float,curLine))# 将每行映射成为浮点数
12         dataMat.append(fltLine)
13     return dataMat
14 
15 # 2.将数据切分文两个集合并返回
16 def binSplitDataSet(dataSet,feature,value):
17     # 原文有误
18     mat0=dataSet[nonzero(dataSet[:,feature]>value)[0],:]
19     mat1=dataSet[nonzero(dataSet[:,feature]<=value)[0],:]
20     return mat0,mat1
21 
22 # 3.生成叶节点，目标变量的均值
23 def regLeaf(dataSet):
24     return mean(dataSet[:,-1])
25 
26 # 4.误差估计函数，目标变量的平方误差和
27 def regErr(dataSet):
28     return var(dataSet[:,-1])*shape(dataSet)[0]
29 
30 # 5.选择最好的区分方式
31 def chooseBestSplit(dataSet,leafType=regLeaf,errType=regErr,ops=(1,4)):
32     # tols：容许的误差下降值，toln：切分的最少样本数
33     tolS=ops[0];tolN=ops[1]
34     # 如果数据集所有值相等则退出
35     if len(set(dataSet[:,-1].T.tolist()[0]))==1:
36         return None,leafType(dataSet)
37     # 初始化
38     m,n=shape(dataSet)
39     S=errType(dataSet)
40     bestS=inf;bestIndex=0;bestValue=0
41     # 从第一个特征循环遍历到最后一个特征，注意最后一列为标签值
42     for featIndex in range(n-1):
43         # 从某特征第一个值遍历到最后一个值
44         # 与原文不一致
45         for splitVal in set(dataSet[:,featIndex].T.tolist()[0]):
46             # 切分数据集
47             mat0,mat1=binSplitDataSet(dataSet,featIndex,splitVal)
48             # 如果某一边样本数小于最少样本数，则重新切分
49             if (shape(mat0)[0]<tolN)or(shape(mat1)[0]<tolN):
50                 continue
51             # 找到最小误差，并记录特征和拆分值
52             newS=errType(mat0)+errType(mat1)
53             if newS<bestS:
54                 bestIndex=featIndex
55                 bestValue=splitVal
56                 bestS=newS
57             if (S-bestS)<tolS:
58                 return None,leafType(dataSet)
59     mat0,mat1=binSplitDataSet(dataSet,bestIndex,bestValue)
60     if (shape(mat0)[0]<tolN)or(shape(mat1)[0]<tolN):
61         return None,leafType(dataSet)
62     return bestIndex,bestValue
63 
64 # 6.创建树
65 def createTree(dataSet,leafType=regLeaf,errType=regErr,ops=(1,4)):
66     feat,val = chooseBestSplit(dataSet,leafType,errType,ops)
67     if feat==None:
68         return val
69     retTree={}
70     retTree['spInd']=feat
71     retTree['spVal']=val
72     lSet , rSet = binSplitDataSet(dataSet,feat,val)
73     retTree['left']=createTree(lSet,leafType,errType,ops)
74     retTree['right']=createTree(rSet,leafType,errType,ops)
75     return retTree
76 
77 myData1=loadDataSet("ex0.txt")
78 myMat1=mat(myData1)
79 mytree1=createTree(myMat1)
80 print(mytree1)
View Code

　　输出结果：

2.2 树剪枝

1. 预剪枝：

    • 以上程序中tolS和tolN分别为：容许的误差下降值、切分的最少样本数。

    • 尝试修改上面程序中的tolS和tolN，会发现输出的树差别会很大。树构建算法对此十分敏感，使用某些值会达到很好的效果，其他则效果差。

    • 这个条件约束其实就是一种预剪枝操作，但如果一直尝试看那一组约束值效果最好，就不够智能了，如此，我们需要后剪枝。

2. 后剪枝：

    • 后剪枝需要训练集和测试集，训练集用来构建基础树，测试集就是用来剪枝操作。

    • 基于已有的树进行剪枝：

      • 如果存在任意子集是一棵树，则在该子集递归剪枝过程

      • 计算当前两叶节点合并后的误差与合并前的误差，如果合并后误差降低，则合并，即起到剪枝效果。

剪枝操作的几个函数代码：

 1 # 7.后剪枝
 2 # 判断有无子树
 3 def isTree(obj):
 4     return (type(obj).__name__=='dict')
 5 # 计算平均值
 6 def getMean(tree):
 7     if isTree(tree['right']):
 8         tree['right']=getMean(tree['right'])
 9     if isTree(tree['left']):
10         tree['left']=getMean(tree['left'])
11     return (tree['left']+tree['right'])/2.0
12 # 剪枝处理
13 def prune(tree,testData):
14     if shape(testData)[0]==0:
15         return getMean(tree)
16     if (isTree(tree['right']) or isTree(tree['left'])):
17         lSet,rSet=binSplitDataSet(testData,tree['spInd'],tree['spVal'])
18     # 递归过程
19     if (isTree(tree['left'])):
20         tree['left']=prune(tree['left'],rSet)
21     if (isTree(tree['right'])):
22         tree['right']=prune(tree['right'],rSet)
23     # 当左右树没有子树时，合并：如果合并后误差小于合并前则进行合并，如果大则不合并
24     if not isTree(tree['left']) and not isTree(tree['right']):
25         lSet,rSet=binSplitDataSet(testData,tree['spInd'],tree['spVal'])
26         errorNoMerge=sum(power(lSet[:,-1]-tree['left'],2))+ \
27                      sum(power(rSet[:, -1] - tree['right'], 2))
28         treeMean=(tree['left']+tree['right'])/2.0
29         errorMerge=sum(power(testData[:,-1]-treeMean,2))
30         if errorMerge<errorNoMerge:
31             # print("merging")
32             return treeMean
33         else:
34             return tree
35     else:
36         return tree
37     
38 myData2=loadDataSet("ex2.txt")
39 myMat2=mat(myData2)
40 mytree2=createTree(myMat2,ops=(0,1))
41 myDataTest=loadDataSet('ex2test.txt')
42 myMatTest=mat(myDataTest)
43 mytree2_pruned=prune(mytree2,myMatTest)
44 print(mytree2)
45 print(mytree2_pruned)
View Code

后剪枝可能不如预剪枝有效，有时需要混合双剪。

2.3 模型树

以上，我们是把节点简单的设置为常数值，但构造的树有时过于复杂，不是很好用。如下图 (exp2.txt) 是一组原数据：

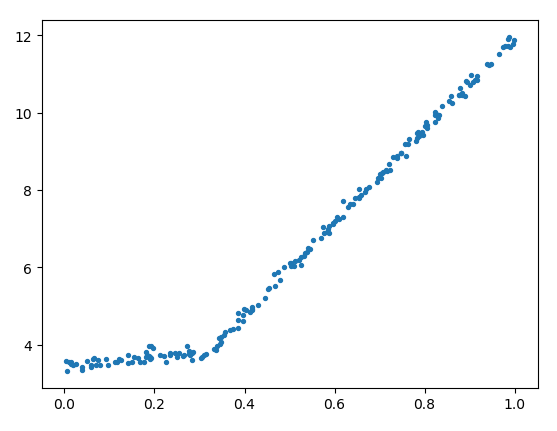
如果我们使用以上程序构造一个树，比较复杂，结果如下：

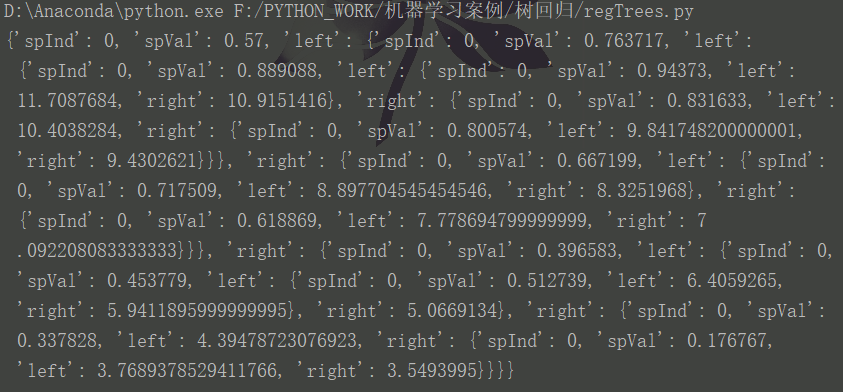
　　很显然，这里的数据是一个分段线性函数。此时我们使用了一个方法：将叶节点处的常数值改成线性模型。

　　函数程序如下：

 1 # 8.模型树
 2 # 简单的线性回归
 3 def linearSolve(dataSet):
 4     m,n=shape(dataSet)
 5     X=mat(ones((m,n)))
 6     Y=mat(ones((m,1)))
 7     X[:,1:n]=dataSet[:,0:n-1]
 8     Y=dataSet[:,-1]
 9     xTx=X.T*X
10     if linalg.det(xTx)==0.0:
11         raise NameError('this matrix is singular,cannot do inverse,try increasing the second value of ops')
12     ws= xTx.I*(X.T*Y)
13     return ws,X,Y
14 # 生成节点模型，此处即线性回归的回归系数
15 def modelLeaf(dataSet):
16     ws,X,Y=linearSolve(dataSet)
17     return ws
18 # 计算数据集误差
19 def modelErr(dataSet):
20     ws,X,Y=linearSolve(dataSet)
21     yHat=X*ws
22     return sum(power(Y-yHat,2))
23 
24 myData2=loadDataSet("exp2.txt")
25 myMat2=mat(myData2)
26 fig=plt.figure()
27 ax=fig.add_subplot(111)
28 ax.scatter(myMat2[:,0].A,myMat2[:,1].A,s=8)
29 plt.show()
30 tree1=createTree(myMat2,leafType=modelLeaf,errType=modelErr,ops=(1,10))
31 tree2=createTree(myMat2,ops=(0.1,10))
32 print(tree1)
33 # print(tree2)
View Code

　　结果如下：

　　看上去，与图差不多啦。

3 示例：树回归与标准回归的比较

　　本例讲的是，骑车速度与人智商的关系（真是智障==，这数据是外国人造的），数据可视如下：

 

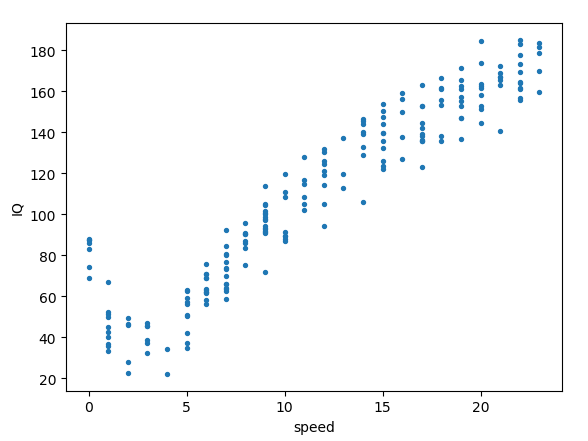
上面程序中没有提到预测，只是构建了基于训练集的树，下面给出预测相关函数程序：

 1 # 9.树回归预测代码
 2 # 常数值叶节点进行预测，使用均值，使用两个输入参数是为与模型树节点保持一致
 3 def regTreeEval(model,inDat):
 4     return float(model)
 5 # 线性模型叶节点进行预测，使用线性回归值
 6 def modelTreeEval(model,inDat):
 7     n=shape(inDat)[1]
 8     X=mat(ones((1,n+1)))
 9     X[:,1:n+1]=inDat
10     return float(X*model)
11 # 预测某一数据点
12 def treeForeCast(tree,inData,modelEval=regTreeEval):
13     # 没有子树时，便返回预测结果
14     if not isTree(tree):
15         return modelEval(tree,inData)
16     # 大于节点的值放入左树中，小于节点的值放入有树中
17     if inData[tree['spInd']]>tree['spVal']:
18         if isTree(tree['left']):
19             return treeForeCast(tree['left'],inData,modelEval)
20         else:
21             return modelEval(tree['left'],inData)
22     else:
23         if isTree(tree['right']):
24             return treeForeCast(tree['right'],inData,modelEval)
25         else:
26             return modelEval(tree['right'],inData)
27 # 预测testdata，返回一组向量
28 def createForeCast(tree,testData,modelEval=regTreeEval):
29     m=len(testData)
30     yHat=mat(zeros((m,1)))
31     for i in range(m):
32         yHat[i,0]=treeForeCast(tree,mat(testData[i]),modelEval)
33     return yHat
View Code

4 附加：使用Tkinter库创建GUI

　   程序：

 1 from numpy import *
 2 from tkinter import *
 3 # 设定matplotlib的后端为Tkagg
 4 import matplotlib
 5 matplotlib.use('TkAgg')
 6 # tkagg和matplotlib图连接起来
 7 from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
 8 from matplotlib.figure import Figure
 9 import regTrees
10 
11 def reDraw(tolS,tolN):
12     reDraw.f.clf()
13     reDraw.a=reDraw.f.add_subplot(111)
14     if chkBtnVar.get():
15         if tolN < 2:
16             tolN = 2
17         myTree = regTrees.createTree(reDraw.rawDat, regTrees.modelLeaf, \
18                                      regTrees.modelErr, (tolS, tolN))
19         yHat = regTrees.createForeCast(myTree, reDraw.testDat, \
20                                        regTrees.modelTreeEval)
21     else:
22         myTree = regTrees.createTree(reDraw.rawDat, ops=(tolS, tolN))
23         yHat = regTrees.createForeCast(myTree, reDraw.testDat)
24     reDraw.a.scatter(reDraw.rawDat[:, 0].A, reDraw.rawDat[:, 1].A, s=5)
25     reDraw.a.plot(reDraw.testDat, yHat, linewidth=2.0)
26     reDraw.canvas.draw()
27 
28 def getInputs():
29     try:
30         tolN = int(tolNentry.get())
31     except:
32         tolN = 10
33         print("enter Integer for tolN")
34         tolNentry.delete(0, END)
35         tolNentry.insert(0,'10')
36     try:
37         tolS = float(tolSentry.get())
38     except:
39         tolS = 1.0
40         print("enter Float for tolS")
41         tolSentry.delete(0, END)
42         tolSentry.insert(0,'1.0')
43     return tolN,tolS
44 
45 def drawNewTree():
46     tolN,tolS = getInputs()#get values from Entry boxes
47     reDraw(tolS,tolN)
48 
49 root=Tk()
50 
51 # 用网格布局管理器安排位置
52 reDraw.f=Figure(figsize=(5,4),dpi=100)
53 reDraw.canvas=FigureCanvasTkAgg(reDraw.f,master=root)
54 reDraw.canvas.get_tk_widget().grid(row=0,columnspan=3)
55 reDraw.canvas.draw()
56 
57 # Label(root,text="plot place holder").grid(row=0,columnspan=3)
58 Label(root,text="tolN").grid(row=1,column=0)
59 tolNentry=Entry(root)
60 tolNentry.grid(row=1,column=1)
61 tolNentry.insert(0,'10')
62 
63 Label(root,text="tolS").grid(row=2,column=0)
64 tolSentry=Entry(root)
65 tolSentry.grid(row=2,column=1)
66 tolSentry.insert(0,'1.0')
67 
68 Button(root,text="redraw",command=drawNewTree).grid(row=1,column=2,rowspan=3)
69 
70 chkBtnVar=IntVar()
71 chkBtn=Checkbutton(root,text="model tree",variable=chkBtnVar)
72 chkBtn.grid(row=3,column=0,columnspan=2)
73 
74 reDraw.rawDat = mat(regTrees.loadDataSet("sine.txt"))
75 reDraw.testDat = arange(min(reDraw.rawDat[:, 0]), max(reDraw.rawDat[:, 0]), 0.01)
76 reDraw(1,10)
77 root.mainloop()
View Code

 

posted @ 2019-05-28 18:30  滇红88号  阅读(240)  评论(0)  编辑  收藏  举报