机器学习实战4-SVM
1 SVM解释

-
通俗的讲,就是用来分类的。
-
对于以上二维数据,支持向量就是那三个站在虚线上的点,中间那个粗黑硬实线表示的就是分割面(即超平面),可以将以上扩展到无数维,当然你肯定想象不出100维时是个什么样子。
-
图上两虚线之间的距离称作间隔。
-
我们的目标就是使间隔能够最大化,最大化间隔意味着可以更好的分类,即找到合适的超平面(就是那个黑粗硬实线),即求参数w和b。
-
利用SMO算法可以高效解决4中问题
阅读周志华《机器学习》
2 SMO理解与简易实现
关于SMO算法过程可以阅读本篇文章:https://zhuanlan.zhihu.com/p/29212107
关于边界值C:可以理解为SVM对“软间隔的支持度”,C如果为无穷大,则所有的训练
样本必须满足SVM的约束条件,C值越小,就允许越多的样本不满足约束条件。
谈下几个主要过程:
- 初始化,需要数据集及其标签,常数C,容错率,最大循环次数
- while(确保α达到最优状态):得到优化后的α和b
- for(从1一直循环到m):
- 固定αi,计算fxi和ei
- 判断αi是否已在边界上,在就不能继续优化
- 计算fxj,ej
- 计算αj的上下界L,H等相关的值
- 更新αj
- 更新αi
- 更新阈值b
- for(从1一直循环到m):
- 返回w和b
看上去好像更糊涂=。=,还是看上面的算法文章靠谱,以下是代码的简易实现:
1 from numpy import * 2 import matplotlib.pyplot as plt 3 4 # 导入文件数据 5 def loadDataSet(fileName): 6 dataMat=[] 7 labelMat=[] 8 fr=open(fileName) 9 for line in fr.readlines(): 10 lineArr=line.strip().split('\t') 11 dataMat.append([float(lineArr[0]),float(lineArr[1])]) 12 labelMat.append(float(lineArr[2])) 13 return dataMat,labelMat 14 15 # m为alpha个数,i为下标,随机输出与i不同的j 16 def selectJrand(i,m): 17 j=i 18 while(j==i): 19 j=int(random.uniform(0,m)) 20 return j 21 22 # 用于调整大于H、或者小于L的alpha 23 def clipAlpha(aj,H,L): 24 if aj>H: 25 aj=H 26 if L>aj: 27 aj=L 28 return aj 29 30 # 简化版本SMO算法 31 def smoSimple(dataMatIn,classLabels,C,toler,maxIter): 32 # 初始化条件,数据集,类别标签,常数C,容错率和取消前最大的循环次数 33 dataMatrix=mat(dataMatIn) 34 labelMat=mat(classLabels).transpose() 35 b=0;m,n=shape(dataMatrix) 36 alphas=mat(zeros((m,1))) 37 iter=0 38 39 while(iter<maxIter): 40 alphaPairsChanged=0 # alphapaitchanged 是否已进行优化 41 for i in range(m): 42 # 与周志华机器学习公式有一丝区别:x为m*n矩阵 周志华中xm为列向量,此处为行向量 43 # 即公式为f(xi) = ∑alpha_mi*y_mi*x_mi*xi.T + b 可理解为距离 f(x)为m维行向量 44 fXi=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T))+b # multiply为对应元素相乘 45 Ei=fXi-float(labelMat[i]) # 计算偏差 46 # 判断条件:正负间隔均判断,同时检查alpha值,保证其不等于C或者0 47 if ((labelMat[i]*Ei<-toler)and(alphas[i]<C)) or ((labelMat[i]*Ei>toler)and(alphas[i]>0)): 48 j=selectJrand(i,m) #取不同于i的j 49 fXj=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T))+b 50 Ej = fXj - float(labelMat[j]) 51 alphaIold=alphas[i].copy() 52 alphaJold=alphas[j].copy() 53 # 计算L、H,即alpha_j的上下界 54 if(labelMat[i]!=labelMat[j]): 55 L=max(0,alphas[j]-alphas[i]) 56 H=min(C,C+alphas[j]-alphas[i]) 57 else: 58 L=max(0,alphas[j]+alphas[i]-C) 59 H=min(C,alphas[j]+alphas[i]) 60 if L==H: 61 # print("L=H") 62 continue 63 # η=-(K11+K22−2K12)也可去掉负号,但相应更新alpha_j时累减改成累加 64 eta=2.0*dataMatrix[i,:]*dataMatrix[j,:].T-\ 65 dataMatrix[i,:]*dataMatrix[i,:].T-\ 66 dataMatrix[j,:]*dataMatrix[j,:].T 67 if eta>=0: 68 # print("eta>=0") 69 continue 70 # 更新alpha_j 71 alphas[j]-=labelMat[j]*(Ei-Ej)/eta 72 alphas[j]=clipAlpha(alphas[j],H,L) 73 if(abs(alphas[j]-alphaJold)<0.00001): 74 # print("j not moving enough") 75 continue 76 # 更新alpha_i 77 alphas[i]+=labelMat[j]*labelMat[i]*(alphaJold-alphas[j]) 78 # 更新阈值b 79 b1=b-Ei-labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T-\ 80 labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T 81 b2=b-Ej-labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T-\ 82 labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T 83 if (0<alphas[i])and(C>alphas[i]): 84 b=b1 85 elif (0<alphas[j])and(C>alphas[j]): 86 b=b2 87 else: 88 b=(b1+b2)/2.0 89 alphaPairsChanged+=1 90 # print("iter:%d i:%d,pairs changed %d"%(iter,i,alphaPairsChanged)) 91 if(alphaPairsChanged==0): 92 iter+=1 93 else: 94 iter=0 95 # print("iteration number: %d"%iter) 96 return b,alphas 97 98 # 分类数据点 99 def classPts(dataArr,labelArr): 100 classifiedPts = {'+1': [], '-1': []} 101 # zip 进行封装,返回的是一个对象,可用list将其转换为列表查看 102 for point, label in zip(dataArr, labelArr): 103 if label == 1.0: 104 classifiedPts['+1'].append(point) 105 else: 106 classifiedPts['-1'].append(point) 107 return classifiedPts 108 109 # 通过已知数据点和拉格朗日乘子获得分割超平面参数w 110 def get_w(alphas, dataset, labels): 111 import numpy as np 112 alphas, dataset, labels = np.array(alphas), np.array(dataset), np.array(labels) 113 yx = labels.reshape(1, -1).T*np.array([1, 1])*dataset 114 w = np.dot(yx.T, alphas) 115 return w.tolist() 116 117 # 绘制数据点,分割线,支持向量 118 def drawSvm(classPts,alphas,dataArr,labelArr): 119 # 绘制数据点 120 import numpy as ny 121 for label, pts in classPts.items(): 122 pts = ny.array(pts) 123 ax.scatter(pts[:, 0], pts[:, 1], label=label) 124 # 绘制分割线 125 w = get_w(alphas, dataArr, labelArr) 126 x1, _ = max(dataArr, key=lambda x: x[0]) 127 x2, _ = min(dataArr, key=lambda x: x[0]) 128 a1, a2 = w 129 y1, y2 = (-float(b) - a1[0]*x1)/a2[0], (-float(b) -a1[0]*x2)/a2[0] # b是矩阵类型,a1是列表类型,x1是float,注意不同形式之间的转换 130 ax.plot([x1, x2], [y1, y2]) 131 # 绘制支持向量 132 for i, alpha in enumerate(alphas): 133 if abs(alpha) > 1e-3: 134 x, y = dataArr[i] 135 ax.scatter([x], [y], s=150, c='none', alpha=0.7, 136 linewidth=1.5, edgecolor='#AB3319') 137 plt.show() 138 139 140 141 dataArr,labelArr=loadDataSet('testSet.txt') 142 b,alphas=smoSimple(dataArr,labelArr,0.6,0.001,40) 143 classFieldPts=classPts(dataArr,labelArr) 144 ax = plt.figure().add_subplot(111) 145 drawSvm(classFieldPts,alphas,dataArr,labelArr)
输出结果:
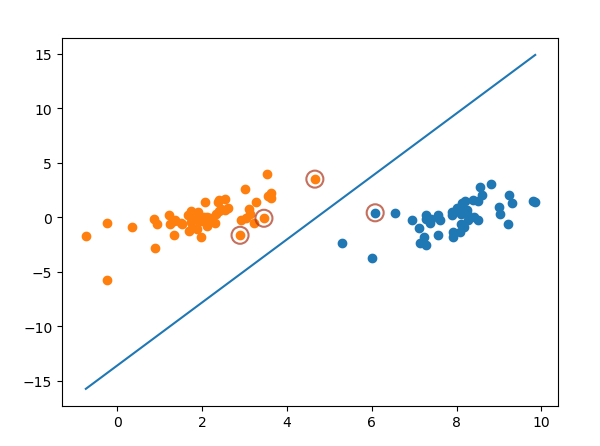
3 完整版Platt SMO算法
目的:为了进一步优化算法,起到加速作用
| 简版SMO | 完整Platt SMO | |
| while循环 |
退出条件: 迭代次数超过指定最大次数
|
退出条件: 1.迭代次数超过指定最大次数 2.遍历整个集合都未对任意alpha对进行修改 |
|
iter: 当没有任何alpha值发生变化 时,计一次迭代,即iter+1 |
iter: 作为一次循环过程,即每一次循环iter+1
|
|
| while循环内 |
选择j后会计算错误率Ej (右边的算法则使用一个全局 缓存保存误差值,选择Ei-Ej 最大的alpha值) |
1.遍历任意可能的alpha 通过inneL选择第二个alpha,可能时进行优化处理 2.遍历所有非边界(即不在边界0或者C上)alpha值 在以上两种方式中进行切换 |
完整代码:

1 from numpy import * 2 import matplotlib.pyplot as plt 3 4 # 导入文件数据 5 def loadDataSet(fileName): 6 dataMat=[] 7 labelMat=[] 8 fr=open(fileName) 9 for line in fr.readlines(): 10 lineArr=line.strip().split('\t') 11 dataMat.append([float(lineArr[0]),float(lineArr[1])]) 12 labelMat.append(float(lineArr[2])) 13 return dataMat,labelMat 14 15 # m为alpha个数,i为下标,随机输出与i不同的j 16 def selectJrand(i,m): 17 j=i 18 while(j==i): 19 j=int(random.uniform(0,m)) 20 return j 21 22 # 用于调整大于H、或者小于L的alpha 23 def clipAlpha(aj,H,L): 24 if aj>H: 25 aj=H 26 if L>aj: 27 aj=L 28 return aj 29 30 # 简化版本SMO算法 31 def smoSimple(dataMatIn,classLabels,C,toler,maxIter): 32 # 初始化条件,数据集,类别标签,常数C,容错率和取消前最大的循环次数 33 dataMatrix=mat(dataMatIn) 34 labelMat=mat(classLabels).transpose() 35 b=0;m,n=shape(dataMatrix) 36 alphas=mat(zeros((m,1))) 37 iter=0 38 39 while(iter<maxIter): 40 alphaPairsChanged=0 # alphapaitchanged 是否已进行优化 41 for i in range(m): 42 # 与周志华机器学习公式有一丝区别:x为m*n矩阵 周志华中xm为列向量,此处为行向量 43 # 即公式为f(xi) = ∑alpha_mi*y_mi*x_mi*xi.T + b 可理解为距离 f(x)为m维行向量 44 fXi=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T))+b # multiply为对应元素相乘 45 Ei=fXi-float(labelMat[i]) # 计算偏差 46 # 判断条件:正负间隔均判断,同时检查alpha值,保证其不等于C或者0 47 if ((labelMat[i]*Ei<-toler)and(alphas[i]<C)) or ((labelMat[i]*Ei>toler)and(alphas[i]>0)): 48 j=selectJrand(i,m) #取不同于i的j 49 fXj=float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T))+b 50 Ej = fXj - float(labelMat[j]) 51 alphaIold = alphas[i].copy() 52 alphaJold=alphas[j].copy() 53 # 计算L、H,即alpha_j的上下界 54 if(labelMat[i]!=labelMat[j]): 55 L = max(0, alphas[j]-alphas[i]) 56 H = min(C, C+alphas[j]-alphas[i]) 57 else: 58 L=max(0, alphas[j]+alphas[i]-C) 59 H=min(C, alphas[j]+alphas[i]) 60 if L==H: 61 # print("L=H") 62 continue 63 # η=-(K11+K22−2K12)也可去掉负号,但相应更新alpha_j时累减改成累加 64 eta=2.0*dataMatrix[i,:]*dataMatrix[j,:].T-\ 65 dataMatrix[i,:]*dataMatrix[i,:].T-\ 66 dataMatrix[j,:]*dataMatrix[j,:].T 67 if eta>=0: 68 # print("eta>=0") 69 continue 70 # 更新alpha_j 71 alphas[j]-=labelMat[j]*(Ei-Ej)/eta 72 alphas[j]=clipAlpha(alphas[j],H,L) 73 if(abs(alphas[j]-alphaJold)<0.00001): 74 # print("j not moving enough") 75 continue 76 # 更新alpha_i 77 alphas[i]+=labelMat[j]*labelMat[i]*(alphaJold-alphas[j]) 78 # 更新阈值b 79 b1=b-Ei-labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T-\ 80 labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T 81 b2=b-Ej-labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T-\ 82 labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T 83 if (0<alphas[i])and(C>alphas[i]): 84 b=b1 85 elif (0<alphas[j])and(C>alphas[j]): 86 b=b2 87 else: 88 b=(b1+b2)/2.0 89 alphaPairsChanged+=1 90 # print("iter:%d i:%d,pairs changed %d"%(iter,i,alphaPairsChanged)) 91 if(alphaPairsChanged==0): 92 iter+=1 93 else: 94 iter=0 95 # print("iteration number: %d"%iter) 96 return b,alphas 97 98 # 1. 构建一个数据结构存储所有数据 99 class optStruct: 100 def __init__(self, dataMatIn, classLabels, C, toler): 101 self.X = dataMatIn 102 self.labelMat = classLabels 103 self.C = C 104 self.tol = toler 105 self.m = shape(dataMatIn)[0] 106 self.alphas = mat(zeros((self.m,1))) 107 self.b = 0 108 self.eCache = mat(zeros((self.m,2))) # 误差缓存 第一列是eCache是否有效的标志位,第二列是实际E值 109 110 # 2. 计算k处误差值 111 def calcEk(oS,k): 112 fXk = float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T))+oS.b 113 Ek = fXk-float(oS.labelMat[k]) 114 return Ek 115 116 # 3. 用于选择第二个α 117 def selectJ(i,oS,Ei): 118 maxK = -1 ; maxDeltaE = 0 ; Ej = 0 119 oS.eCache[i]=[1,Ei] 120 validEcacheList = nonzero(oS.eCache[:,0].A)[0] # nonzero 返回数组中非零元素的索引值 121 if (len(validEcacheList)) > 1: 122 # 遍历一遍上列表,找出最大差值的Ej 123 for k in validEcacheList: 124 if k == i: 125 continue 126 Ek = calcEk(oS,k) 127 deltaE = abs(Ei-Ek) 128 if (deltaE>maxDeltaE): 129 maxK=k 130 maxDeltaE=deltaE 131 Ej=Ek 132 return maxK,Ej 133 else: 134 # 第一次,直接随机寻找一个Ej 135 j=selectJrand(i,oS.m) 136 Ej=calcEk(oS,j) 137 return j,Ej 138 139 # 4. 计算k处误差值 并存入eCache中 140 def updateEk(oS,k): 141 Ek=calcEk(oS,k) 142 oS.eCache[k]=[1,Ek] 143 144 # 5. 内部循环,找到配对Ej,则返回1, 145 def innerL(i,oS): 146 Ei=calcEk(oS,i) 147 if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or \ 148 ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)): 149 j,Ej=selectJ(i,oS,Ei) 150 alphaIold=oS.alphas[i].copy() 151 alphaJold=oS.alphas[j].copy() 152 if (oS.labelMat[i] != oS.labelMat[j]): 153 L = max(0, oS.alphas[j] - oS.alphas[i]) 154 H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) 155 else: 156 L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C) 157 H = min(oS.C, oS.alphas[j] + oS.alphas[i]) 158 if L == H: 159 print("L=H") 160 return 0 161 eta=2.0*oS.X[i,:]*oS.X[j,:].T-oS.X[i,:]*oS.X[i,:].T-\ 162 oS.X[j,:]*oS.X[j,:].T 163 if eta >= 0: 164 print("eta>=0") 165 return 0 166 oS.alphas[j]-=oS.labelMat[j]*(Ei-Ej)/eta 167 oS.alphas[j]=clipAlpha(oS.alphas[j],H,L) 168 updateEk(oS,j) 169 if (abs(oS.alphas[j] - alphaJold) < 0.00001): 170 print("j not moving enough") 171 return 0 172 oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j]) 173 updateEk(oS, i) 174 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * ( 175 oS.alphas[j] - alphaJold) * oS.X[i, :] * oS.X[j, :].T 176 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * ( 177 oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T 178 if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): 179 oS.b = b1 180 elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): 181 oS.b = b2 182 else: 183 oS.b = (b1 + b2) / 2.0 184 return 1 185 else: 186 return 0 187 188 # 6. 完整函数 189 def smoP(dataMatIn, classLabels, C, toler, maxIter): 190 # 创建一个 optStruct 对象 191 oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler) 192 iter = 0 193 entireSet = True 194 alphaPairsChanged = 0 195 # 循环遍历:循环maxIter次 并且 (alphaPairsChanged存在可以改变 or 所有行遍历一遍) 196 # 循环迭代结束 或者 循环遍历所有alpha后,alphaPairs还是没变化 197 while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): 198 alphaPairsChanged = 0 199 # 当entireSet=true or 非边界alpha对没有了;就开始寻找 alpha对,然后决定是否要进行else。 200 if entireSet: 201 # 在数据集上遍历所有可能的alpha 202 for i in range(oS.m): 203 # 是否存在alpha对,存在就+1 204 alphaPairsChanged += innerL(i, oS) 205 print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged)) 206 iter += 1 207 # 对已存在 alpha对,选出非边界的alpha值,进行优化。 208 else: 209 # 遍历所有的非边界alpha值,也就是不在边界0或C上的值。 210 nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] 211 for i in nonBoundIs: 212 alphaPairsChanged += innerL(i, oS) 213 print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged)) 214 iter += 1 215 # 如果找到alpha对,就优化非边界alpha值,否则,就重新进行寻找,如果寻找一遍 遍历所有的行还是没找到,就退出循环。 216 if entireSet: 217 entireSet = False # toggle entire set loop 218 elif (alphaPairsChanged == 0): 219 entireSet = True 220 print("iteration number: %d" % iter) 221 return oS.b, oS.alphas 222 223 # 7. 通过已知数据点和拉格朗日乘子获得分割超平面参数w 224 def calcWs(alphas, dataArr, classLabels): 225 X = mat(dataArr) 226 labelMat = mat(classLabels).transpose() 227 m, n = shape(X) 228 w = zeros((n, 1)) 229 for i in range(m): 230 w += multiply(alphas[i] * labelMat[i], X[i, :].T) 231 return w 232 233 # 8. 绘制数据点,分割线,支持向量 234 def drawSvm(alphas,dataArr,labelArr): 235 # 对数据点进行分类 236 classifiedPts = {'+1': [], '-1': []} 237 # zip 进行封装,返回的是一个对象,可用list将其转换为列表查看 238 for point, label in zip(dataArr, labelArr): 239 if label == 1.0: 240 classifiedPts['+1'].append(point) 241 else: 242 classifiedPts['-1'].append(point) 243 ax = plt.figure().add_subplot(111) 244 # 绘制数据点 245 import numpy as ny 246 for label, pts in classifiedPts.items(): 247 pts = ny.array(pts) 248 ax.scatter(pts[:, 0], pts[:, 1], label=label) 249 # 绘制分割线 250 w = calcWs(alphas, dataArr, labelArr) 251 x1, _ = max(dataArr, key=lambda x: x[0]) 252 x2, _ = min(dataArr, key=lambda x: x[0]) 253 a1, a2 = w 254 y1, y2 = (-float(b) - a1[0]*x1)/a2[0], (-float(b) -a1[0]*x2)/a2[0] # b是矩阵类型,a1是列表类型,x1是float,注意不同形式之间的转换 255 ax.plot([x1, x2], [y1, y2]) 256 # 绘制支持向量 257 for i, alpha in enumerate(alphas): 258 if abs(alpha) > 1e-3: 259 x, y = dataArr[i] 260 ax.scatter([x], [y], s=150, c='none', alpha=0.7, 261 linewidth=1.5, edgecolor='#AB3319') 262 plt.show() 263 264 dataArr,labelArr=loadDataSet('testSet.txt') 265 b,alphas=smoP(dataArr,labelArr,0.9,0.001,40) 266 drawSvm(alphas,dataArr,labelArr)
输出结果:

4 利用核函数将数据映射到高维空间
可以将原始空间映射到一个更高维的特征空间,使得样本在这个高维空间中可以线性可分。如下图:

常用核函数如下:

核转换函数程序如下:
1 # 核转换函数 2 def kernelTrans(X,A,kTup): 3 m,n=shape(X) 4 K=mat(zeros((m,1))) 5 if kTup[0]=='lin': 6 # 线性核函数 7 K=X*A.T 8 elif kTup[0]=='rbf': 9 # 高斯核函数 10 for j in range(m): 11 deltaRow =X[j,:]-A 12 K[j]=deltaRow*deltaRow.T 13 K=exp(K/(-1*kTup[1]**2)) 14 else: 15 raise NameError('houston we have a problem that kenel is not recognized') 16 return K
使用核函数进行svm分类总程序及结果如下:

1 from numpy import * 2 import matplotlib.pyplot as plt 3 4 # 导入文件数据 5 def loadDataSet(fileName): 6 dataMat=[] 7 labelMat=[] 8 fr=open(fileName) 9 for line in fr.readlines(): 10 lineArr=line.strip().split('\t') 11 dataMat.append([float(lineArr[0]),float(lineArr[1])]) 12 labelMat.append(float(lineArr[2])) 13 return dataMat,labelMat 14 15 # m为alpha个数,i为下标,随机输出与i不同的j 16 def selectJrand(i,m): 17 j=i 18 while(j==i): 19 j=int(random.uniform(0,m)) 20 return j 21 22 # 用于调整大于H、或者小于L的alpha 23 def clipAlpha(aj,H,L): 24 if aj>H: 25 aj=H 26 if L>aj: 27 aj=L 28 return aj 29 30 # 核转换函数 31 def kernelTrans(X,A,kTup): 32 m,n=shape(X) 33 K=mat(zeros((m,1))) 34 if kTup[0]=='lin': 35 # 线性核函数 36 K=X*A.T 37 elif kTup[0]=='rbf': 38 # 高斯核函数 39 for j in range(m): 40 deltaRow =X[j,:]-A 41 K[j]=deltaRow*deltaRow.T 42 K=exp(K/(-1*kTup[1]**2)) 43 else: 44 raise NameError('houston we have a problem that kenel is not recognized') 45 return K 46 47 # 1.加核新结构 48 class optStruct: 49 def __init__(self, dataMatIn, classLabels, C, toler,kTup): 50 self.X = dataMatIn 51 self.labelMat = classLabels 52 self.C = C 53 self.tol = toler 54 self.m = shape(dataMatIn)[0] 55 self.alphas = mat(zeros((self.m,1))) 56 self.b = 0 57 self.eCache = mat(zeros((self.m,2))) # 误差缓存 第一列是eCache是否有效的标志位,第二列是实际E值 58 self.K=mat(zeros((self.m,self.m))) 59 # 计算K 60 for i in range(self.m): 61 self.K[:,i]=kernelTrans(self.X,self.X[i,:],kTup) 62 63 # 2.加核新calcEk 64 def calcEk(oS,k): 65 fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k])+oS.b 66 Ek = fXk-float(oS.labelMat[k]) 67 return Ek 68 69 # 3. 用于选择第二个α 70 def selectJ(i,oS,Ei): 71 maxK = -1 ; maxDeltaE = 0 ; Ej = 0 72 oS.eCache[i]=[1,Ei] 73 validEcacheList = nonzero(oS.eCache[:,0].A)[0] # nonzero 返回数组中非零元素的索引值 74 if (len(validEcacheList)) > 1: 75 # 遍历一遍上列表,找出最大差值的Ej 76 for k in validEcacheList: 77 if k == i: 78 continue 79 Ek = calcEk(oS,k) 80 deltaE = abs(Ei-Ek) 81 if (deltaE>maxDeltaE): 82 maxK=k 83 maxDeltaE=deltaE 84 Ej=Ek 85 return maxK,Ej 86 else: 87 # 第一次,直接随机寻找一个Ej 88 j=selectJrand(i,oS.m) 89 Ej=calcEk(oS,j) 90 return j,Ej 91 92 # 4. 计算k处误差值 并存入eCache中 93 def updateEk(oS,k): 94 Ek=calcEk(oS,k) 95 oS.eCache[k]=[1,Ek] 96 97 # 5.加核新innerL 98 def innerL(i,oS): 99 Ei=calcEk(oS,i) 100 if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or \ 101 ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)): 102 j,Ej=selectJ(i,oS,Ei) 103 alphaIold=oS.alphas[i].copy() 104 alphaJold=oS.alphas[j].copy() 105 if (oS.labelMat[i] != oS.labelMat[j]): 106 L = max(0, oS.alphas[j] - oS.alphas[i]) 107 H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) 108 else: 109 L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C) 110 H = min(oS.C, oS.alphas[j] + oS.alphas[i]) 111 if L == H: 112 print("L=H") 113 return 0 114 eta=2.0*oS.K[i,j]-oS.K[i,i]-oS.K[j,j] 115 if eta >= 0: 116 print("eta>=0") 117 return 0 118 oS.alphas[j]-=oS.labelMat[j]*(Ei-Ej)/eta 119 oS.alphas[j]=clipAlpha(oS.alphas[j],H,L) 120 updateEk(oS,j) 121 if (abs(oS.alphas[j] - alphaJold) < 0.00001): 122 print("j not moving enough") 123 return 0 124 oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j]) 125 updateEk(oS, i) 126 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i,i] - \ 127 oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i,j] 128 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i,j] - \ 129 oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j,j] 130 if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): 131 oS.b = b1 132 elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): 133 oS.b = b2 134 else: 135 oS.b = (b1 + b2) / 2.0 136 return 1 137 else: 138 return 0 139 140 # 6. 完整函数 141 def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup): 142 # 创建一个 optStruct 对象 143 oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler,kTup) 144 iter = 0 145 entireSet = True 146 alphaPairsChanged = 0 147 # 循环遍历:循环maxIter次 并且 (alphaPairsChanged存在可以改变 or 所有行遍历一遍) 148 # 循环迭代结束 或者 循环遍历所有alpha后,alphaPairs还是没变化 149 while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): 150 alphaPairsChanged = 0 151 # 当entireSet=true or 非边界alpha对没有了;就开始寻找 alpha对,然后决定是否要进行else。 152 if entireSet: 153 # 在数据集上遍历所有可能的alpha 154 for i in range(oS.m): 155 # 是否存在alpha对,存在就+1 156 alphaPairsChanged += innerL(i, oS) 157 print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged)) 158 iter += 1 159 # 对已存在 alpha对,选出非边界的alpha值,进行优化。 160 else: 161 # 遍历所有的非边界alpha值,也就是不在边界0或C上的值。 162 nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] 163 for i in nonBoundIs: 164 alphaPairsChanged += innerL(i, oS) 165 print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged)) 166 iter += 1 167 # 如果找到alpha对,就优化非边界alpha值,否则,就重新进行寻找,如果寻找一遍 遍历所有的行还是没找到,就退出循环。 168 if entireSet: 169 entireSet = False # toggle entire set loop 170 elif (alphaPairsChanged == 0): 171 entireSet = True 172 print("iteration number: %d" % iter) 173 return oS.b, oS.alphas 174 175 # 7. 通过已知数据点和拉格朗日乘子获得分割超平面参数w 176 def calcWs(alphas, dataArr, classLabels): 177 X = mat(dataArr) 178 labelMat = mat(classLabels).transpose() 179 m, n = shape(X) 180 w = zeros((n, 1)) 181 for i in range(m): 182 w += multiply(alphas[i] * labelMat[i], X[i, :].T) 183 return w 184 185 # 8. 绘制数据点,分割线,支持向量 186 def drawSvm(alphas,dataArr,labelArr): 187 # 对数据点进行分类 188 classifiedPts = {'+1': [], '-1': []} 189 # zip 进行封装,返回的是一个对象,可用list将其转换为列表查看 190 for point, label in zip(dataArr, labelArr): 191 if label == 1.0: 192 classifiedPts['+1'].append(point) 193 else: 194 classifiedPts['-1'].append(point) 195 ax = plt.figure().add_subplot(111) 196 # 绘制数据点 197 import numpy as ny 198 for label, pts in classifiedPts.items(): 199 pts = ny.array(pts) 200 ax.scatter(pts[:, 0], pts[:, 1], label=label) 201 # 绘制分割线 202 w = calcWs(alphas, dataArr, labelArr) 203 x1, _ = max(dataArr, key=lambda x: x[0]) 204 x2, _ = min(dataArr, key=lambda x: x[0]) 205 a1, a2 = w 206 y1, y2 = (-float(b) - a1[0]*x1)/a2[0], (-float(b) -a1[0]*x2)/a2[0] # b是矩阵类型,a1是列表类型,x1是float,注意不同形式之间的转换 207 ax.plot([x1, x2], [y1, y2]) 208 # 绘制支持向量 209 for i, alpha in enumerate(alphas): 210 if abs(alpha) > 1e-3: 211 x, y = dataArr[i] 212 ax.scatter([x], [y], s=150, c='none', alpha=0.7, 213 linewidth=1.5, edgecolor='#AB3319') 214 plt.show() 215 216 # 9.测试函数 217 def testRbf(k1=1.5): 218 dataArr, labelArr = loadDataSet('testSetRBF.txt') 219 b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000,('rbf',k1)) 220 datMat=mat(dataArr) 221 labelMat=mat(labelArr).transpose() 222 svInd=nonzero(alphas.A>0)[0] 223 sVs=datMat[svInd] 224 labelSV=labelMat[svInd] 225 print("there are %d Support Vectors" %shape(sVs)[0]) 226 # 如何利用核函数进行分类 227 m,n=shape(datMat) 228 errorCount=0 229 for i in range(m): 230 kenelEval=kernelTrans(sVs,datMat[i,:],('rbf',k1)) 231 predict=kenelEval.T*multiply(labelSV,alphas[svInd])+b 232 if sign(predict)!=sign(labelArr[i]): 233 errorCount+=1 234 print("the training error rate is %f"%(float(errorCount)/m)) 235 dataArr,labelArr=loadDataSet('testSetRBF2.txt') 236 errorCount=0 237 datMat=mat(dataArr);labelMat=mat(labelArr).transpose() 238 m,n=shape(datMat) 239 for i in range(m): 240 kenelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1)) 241 predict = kenelEval.T * multiply(labelSV, alphas[svInd] )+ b 242 if sign(predict) != sign(labelArr[i]): 243 errorCount += 1 244 print("the training error rate is %f" % (float(errorCount) / m)) 245 246 testRbf()
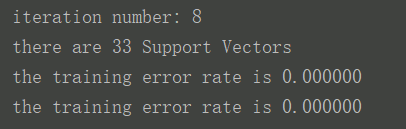
5 实例:手写数据集
可以直接采用前面的函数,不过输入数集需要稍微进行处理。本例有两个文件夹,一个存放训练集,一个存放测试集。每个文件夹中一个文件代表一个一张手写图片,是一个32*32向量,我们需要利用一个函数将其转化为1*1024行向量。将文件夹中所有文件放入矩阵中,这样可以得到训练集矩阵和标签,同样得到测试集矩阵。程序如下:
1 # 将32x32的二进制图像转换为1x1024向量。 2 def img2vector(filename): 3 import numpy as np 4 returnVect = np.zeros((1,1024)) 5 fr = open(filename) 6 for i in range(32): 7 lineStr = fr.readline() 8 for j in range(32): 9 returnVect[0,32*i+j] = int(lineStr[j]) 10 return returnVect 11 12 # 导入数据集和训练集函数 13 def loadImages(dirName): 14 from os import listdir 15 hwLabels = [] 16 trainingFileList = listdir(dirName) # listdir 返回指定文件夹中所有文件及文件夹的名称列表 17 m = len(trainingFileList) 18 trainingMat = zeros((m, 1024)) # 存放训练数据矩阵 19 for i in range(m): 20 fileNameStr = trainingFileList[i] 21 fileStr = fileNameStr.split('.')[0] 22 classNumStr = int(fileStr.split('_')[0]) 23 # hwlabels存放数集标签,1的标签为1,9的标枪为-1 24 if classNumStr == 9: # 如果为9,输出-1 25 hwLabels.append(-1) 26 else: # 如果不为9,输出1 27 hwLabels.append(1) 28 trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr)) # 调用img2vector()函数 29 return trainingMat, hwLabels
识别总代码:

1 # 手写数字集svm识别 1和9 2 import random 3 from numpy import * 4 5 # 将32x32的二进制图像转换为1x1024向量。 6 def img2vector(filename): 7 import numpy as np 8 returnVect = np.zeros((1,1024)) 9 fr = open(filename) 10 for i in range(32): 11 lineStr = fr.readline() 12 for j in range(32): 13 returnVect[0,32*i+j] = int(lineStr[j]) 14 return returnVect 15 16 # 导入数据集和训练集函数 17 def loadImages(dirName): 18 from os import listdir 19 hwLabels = [] 20 trainingFileList = listdir(dirName) # listdir 返回指定文件夹中所有文件及文件夹的名称列表 21 m = len(trainingFileList) 22 trainingMat = zeros((m, 1024)) # 存放训练数据矩阵 23 for i in range(m): 24 fileNameStr = trainingFileList[i] 25 fileStr = fileNameStr.split('.')[0] 26 classNumStr = int(fileStr.split('_')[0]) 27 # hwlabels存放数集标签,1的标签为1,9的标枪为-1 28 if classNumStr == 9: # 如果为9,输出-1 29 hwLabels.append(-1) 30 else: # 如果不为9,输出1 31 hwLabels.append(1) 32 trainingMat[i, :] = img2vector('%s/%s' % (dirName, fileNameStr)) # 调用img2vector()函数 33 return trainingMat, hwLabels 34 35 # m为alpha个数,i为下标,随机输出与i不同的j 36 def selectJrand(i,m): 37 j=i 38 while(j==i): 39 j=int(random.uniform(0,m)) 40 return j 41 42 # 用于调整大于H、或者小于L的alpha 43 def clipAlpha(aj,H,L): 44 if aj>H: 45 aj=H 46 if L>aj: 47 aj=L 48 return aj 49 50 # 核转换函数 51 def kernelTrans(X,A,kTup): 52 m,n=shape(X) 53 K=mat(zeros((m,1))) 54 if kTup[0]=='lin': 55 # 线性核函数 56 K=X*A.T 57 elif kTup[0]=='rbf': 58 # 高斯核函数 59 for j in range(m): 60 deltaRow =X[j,:]-A 61 K[j]=deltaRow*deltaRow.T 62 K=exp(K/(-1*kTup[1]**2)) 63 else: 64 raise NameError('houston we have a problem that kenel is not recognized') 65 return K 66 67 # 1.加核新结构 68 class optStruct: 69 def __init__(self, dataMatIn, classLabels, C, toler,kTup): 70 self.X = dataMatIn 71 self.labelMat = classLabels 72 self.C = C 73 self.tol = toler 74 self.m = shape(dataMatIn)[0] 75 self.alphas = mat(zeros((self.m,1))) 76 self.b = 0 77 self.eCache = mat(zeros((self.m,2))) # 误差缓存 第一列是eCache是否有效的标志位,第二列是实际E值 78 self.K=mat(zeros((self.m,self.m))) 79 # 计算K 80 for i in range(self.m): 81 self.K[:,i]=kernelTrans(self.X,self.X[i,:],kTup) 82 83 # 2.加核新calcEk 84 def calcEk(oS,k): 85 fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k])+oS.b 86 Ek = fXk-float(oS.labelMat[k]) 87 return Ek 88 89 # 3. 用于选择第二个α 90 def selectJ(i,oS,Ei): 91 maxK = -1 ; maxDeltaE = 0 ; Ej = 0 92 oS.eCache[i]=[1,Ei] 93 validEcacheList = nonzero(oS.eCache[:,0].A)[0] # nonzero 返回数组中非零元素的索引值 94 if (len(validEcacheList)) > 1: 95 # 遍历一遍上列表,找出最大差值的Ej 96 for k in validEcacheList: 97 if k == i: 98 continue 99 Ek = calcEk(oS,k) 100 deltaE = abs(Ei-Ek) 101 if (deltaE>maxDeltaE): 102 maxK=k 103 maxDeltaE=deltaE 104 Ej=Ek 105 return maxK,Ej 106 else: 107 # 第一次,直接随机寻找一个Ej 108 j=selectJrand(i,oS.m) 109 Ej=calcEk(oS,j) 110 return j,Ej 111 112 # 4. 计算k处误差值 并存入eCache中 113 def updateEk(oS,k): 114 Ek=calcEk(oS,k) 115 oS.eCache[k]=[1,Ek] 116 117 # 5.加核新innerL 118 def innerL(i,oS): 119 Ei=calcEk(oS,i) 120 if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or \ 121 ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)): 122 j,Ej=selectJ(i,oS,Ei) 123 alphaIold=oS.alphas[i].copy() 124 alphaJold=oS.alphas[j].copy() 125 if (oS.labelMat[i] != oS.labelMat[j]): 126 L = max(0, oS.alphas[j] - oS.alphas[i]) 127 H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) 128 else: 129 L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C) 130 H = min(oS.C, oS.alphas[j] + oS.alphas[i]) 131 if L == H: 132 print("L=H") 133 return 0 134 eta=2.0*oS.K[i,j]-oS.K[i,i]-oS.K[j,j] 135 if eta >= 0: 136 print("eta>=0") 137 return 0 138 oS.alphas[j]-=oS.labelMat[j]*(Ei-Ej)/eta 139 oS.alphas[j]=clipAlpha(oS.alphas[j],H,L) 140 updateEk(oS,j) 141 if (abs(oS.alphas[j] - alphaJold) < 0.00001): 142 print("j not moving enough") 143 return 0 144 oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j]) 145 updateEk(oS, i) 146 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i,i] - \ 147 oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i,j] 148 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i,j] - \ 149 oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j,j] 150 if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): 151 oS.b = b1 152 elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): 153 oS.b = b2 154 else: 155 oS.b = (b1 + b2) / 2.0 156 return 1 157 else: 158 return 0 159 160 # 6. 完整函数 161 def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup): 162 # 创建一个 optStruct 对象 163 oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler,kTup) 164 iter = 0 165 entireSet = True 166 alphaPairsChanged = 0 167 # 循环遍历:循环maxIter次 并且 (alphaPairsChanged存在可以改变 or 所有行遍历一遍) 168 # 循环迭代结束 或者 循环遍历所有alpha后,alphaPairs还是没变化 169 while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)): 170 alphaPairsChanged = 0 171 # 当entireSet=true or 非边界alpha对没有了;就开始寻找 alpha对,然后决定是否要进行else。 172 if entireSet: 173 # 在数据集上遍历所有可能的alpha 174 for i in range(oS.m): 175 # 是否存在alpha对,存在就+1 176 alphaPairsChanged += innerL(i, oS) 177 print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged)) 178 iter += 1 179 # 对已存在 alpha对,选出非边界的alpha值,进行优化。 180 else: 181 # 遍历所有的非边界alpha值,也就是不在边界0或C上的值。 182 nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] 183 for i in nonBoundIs: 184 alphaPairsChanged += innerL(i, oS) 185 print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged)) 186 iter += 1 187 # 如果找到alpha对,就优化非边界alpha值,否则,就重新进行寻找,如果寻找一遍 遍历所有的行还是没找到,就退出循环。 188 if entireSet: 189 entireSet = False # toggle entire set loop 190 elif (alphaPairsChanged == 0): 191 entireSet = True 192 print("iteration number: %d" % iter) 193 return oS.b, oS.alphas 194 195 # 7. 通过已知数据点和拉格朗日乘子获得分割超平面参数w 196 def calcWs(alphas, dataArr, classLabels): 197 X = mat(dataArr) 198 labelMat = mat(classLabels).transpose() 199 m, n = shape(X) 200 w = zeros((n, 1)) 201 for i in range(m): 202 w += multiply(alphas[i] * labelMat[i], X[i, :].T) 203 return w 204 205 # 8. 绘制数据点,分割线,支持向量 206 def drawSvm(alphas,dataArr,labelArr): 207 # 对数据点进行分类 208 classifiedPts = {'+1': [], '-1': []} 209 # zip 进行封装,返回的是一个对象,可用list将其转换为列表查看 210 for point, label in zip(dataArr, labelArr): 211 if label == 1.0: 212 classifiedPts['+1'].append(point) 213 else: 214 classifiedPts['-1'].append(point) 215 ax = plt.figure().add_subplot(111) 216 # 绘制数据点 217 import numpy as ny 218 for label, pts in classifiedPts.items(): 219 pts = ny.array(pts) 220 ax.scatter(pts[:, 0], pts[:, 1], label=label) 221 # 绘制分割线 222 w = calcWs(alphas, dataArr, labelArr) 223 x1, _ = max(dataArr, key=lambda x: x[0]) 224 x2, _ = min(dataArr, key=lambda x: x[0]) 225 a1, a2 = w 226 y1, y2 = (-float(b) - a1[0]*x1)/a2[0], (-float(b) -a1[0]*x2)/a2[0] # b是矩阵类型,a1是列表类型,x1是float,注意不同形式之间的转换 227 ax.plot([x1, x2], [y1, y2]) 228 # 绘制支持向量 229 for i, alpha in enumerate(alphas): 230 if abs(alpha) > 1e-3: 231 x, y = dataArr[i] 232 ax.scatter([x], [y], s=150, c='none', alpha=0.7, 233 linewidth=1.5, edgecolor='#AB3319') 234 plt.show() 235 236 # 9.测试函数 237 def testRbf(k1=1.5): 238 dataArr, labelArr = loadImages('trainingDigits') 239 b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000,('rbf',k1)) 240 datMat=mat(dataArr) 241 labelMat=mat(labelArr).transpose() 242 svInd=nonzero(alphas.A>0)[0] 243 sVs=datMat[svInd] 244 labelSV=labelMat[svInd] 245 print("there are %d Support Vectors" %shape(sVs)[0]) 246 # 如何利用核函数进行分类 247 m,n=shape(datMat) 248 errorCount=0 249 for i in range(m): 250 kenelEval=kernelTrans(sVs,datMat[i,:],('rbf',k1)) 251 predict=kenelEval.T*multiply(labelSV,alphas[svInd])+b 252 if sign(predict)!=sign(labelArr[i]): 253 errorCount+=1 254 print("the training error rate is %f"%(float(errorCount)/m)) 255 dataArr,labelArr=loadImages('testDigits') 256 errorCount=0 257 datMat=mat(dataArr);labelMat=mat(labelArr).transpose() 258 m,n=shape(datMat) 259 for i in range(m): 260 kenelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1)) 261 predict = kenelEval.T * multiply(labelSV, alphas[svInd] )+ b 262 if sign(predict) != sign(labelArr[i]): 263 errorCount += 1 264 print("the training error rate is %f" % (float(errorCount) / m)) 265 266 testRbf()
可以尝试改变k1的值来观察速度和准确率的变化,下图是k1=1.3结果。

本文相关数据集:https://pan.baidu.com/s/1EMODwE2qTtxKEVa6jcrVSw y3xs


 浙公网安备 33010602011771号
浙公网安备 33010602011771号