『模拟赛』CSP-S模拟9

Rank

烂，知耻而后勇

A. 邻面合并

签。

注意到列数 \(m\le 8\)，我们可以直接先搜出每一行可能的“分块”情况，然后转移时枚举上一行的所有状态和这一行的所有状态，根据拼接情况来更新答案，最终答案即为 \(n\) 行所有情况的最小值。

赛时开始打的错解，错解如果第一行总数计算错了就能过小样例（？），然后就改错了，后来打了正解，没改回来能过大样例，而且不是很会打这一题的暴力就没写拍，故挂 30pts。

由于状态那不太会表示，所以存状态用了 vector<vector<int> >，可能不是最优的。

点击查看代码

#include<bits/stdc++.h>
#define fo(x, y, z) for(register int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(register int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{
	char ch = getchar();lx x = 0 , f = 1;
	for(;ch<'0'||ch>'9';ch = getchar()) if(ch == '-') f = -1;
	for(;ch>= '0' && ch<= '9';ch = getchar()) x = (x<<3) + (x<<1) + (ch^48);
	return x*f;
}
#undef lx
#define qr qr()
#define pii pair<int , int>
#define fi first
#define se second
const int Ratio = 0;
const int N = 100 + 5;
int n, m, ans = 1e9;
int d[N][N], zt[N], zc[N];
vector<vector<int> > v[N];
vector<int> f[N];
bool yz[N];
namespace Wisadel
{
    void Wdfs(int hang, int x)
    {
        if(x > m)
        {
            vector<int> cz;
            fo(i, 1, m)
            {
                cz.push_back(zc[i]);
            }
            v[hang].push_back(cz);
            return;
        }
        if(d[hang][x] == 0) zc[x] = 0, Wdfs(hang, x + 1);
        else
        {
            if(d[hang][x - 1] == 1) zc[x] = zc[x - 1], Wdfs(hang, x + 1);
            zc[x] = x, Wdfs(hang, x + 1);
        }
    }
    short main()
    {
        freopen("merging.in", "r", stdin) , freopen("merging.out", "w", stdout);
        n = qr, m = qr;
        fo(i, 1, n) fo(j, 1, m) d[i][j] = qr, zt[i] |= d[i][j] * (1 << (j - 1));
        fo(i, 1, n) Wdfs(i, 1), f[i].resize(v[i].size());
        fo(i, 0, v[1].size() - 1)
        {
            f[1][i] = 0;
            int num = 0;
            fo(j, 0, m - 1)
            {
                if(j == 0 &&v[1][i][j] != 0) num++;
                else if(v[1][i][j] != v[1][i][j - 1] && v[1][i][j] != 0) num++;
            }
            f[1][i] = num;
        }
        fo(i, 2, n)
        {
            fo(k, 0, v[i].size() - 1)
            {
                f[i][k] = 1e9;
                fo(j, 0, v[i - 1].size() - 1)
                {
                    int num = 0, las = v[i][k][0], st = 0; bool lian = 0;
                    fo(z, 1, m - 1)
                    {
                        if(v[i][k][z] != las && las != 0)
                            if(v[i][k][z - 1] != v[i - 1][j][z - 1] || v[i][k][st] != v[i - 1][j][st] || v[i - 1][j][z] == las)
                                num++;
                        if(las != v[i][k][z]) las = v[i][k][z], st = z;
                        if(v[i][k][z] == 0) continue;
                    }
                    if(v[i][k][m - 1] != 0 && (v[i][k][m - 1] != v[i - 1][j][m - 1] || v[i][k][st] != v[i - 1][j][st])) num++;
                    f[i][k] = min(f[i][k], num + f[i - 1][j]);
                }
            }
        }
        fo(i, 0, v[n].size() - 1) ans = min(ans, f[n][i]);
        printf("%d\n", ans);
        return Ratio;
    }
}
int main(){return Wisadel::main();}

B. 光线追踪

由于看到区间（面）修改和单点（线）查询就一下想到了线段树，赛时思路是先离线将询问按斜率升序映射到一个序列上，由于边界等种种问题导致这样很不好实现，由于没开 long long 挂掉可以拿到的 30pts。

用线段树维护关键在想到转换成角度来做。角度范围只有 \(\left[0,\frac{\pi}{2}\right]\)，每次加面相当于是对一定角度做区间推平，查询一个向量相当于是对一个角度做单点查询，理解这种转化后 这题就好说了 还是很恶心。

想到映射就该想到离散化的。考虑每次覆盖一个面对答案有影响的只有下面和左面的两条边，因此有用的三个向量即为原点指向左上、左下、右下三点的向量。我们将它们同询问的向量全部离散化，最多只会有 \(3n\) 个不同的向量，这样它们映射后的下标就形成了一个序列，我们就可以愉快地在上面进行区间修改单点查询的操作了。

不过想必 T2 不会这么容易，还有很多细节要处理。首先是修改后答案是否更改，由小样例可知存在一种这样的情况：

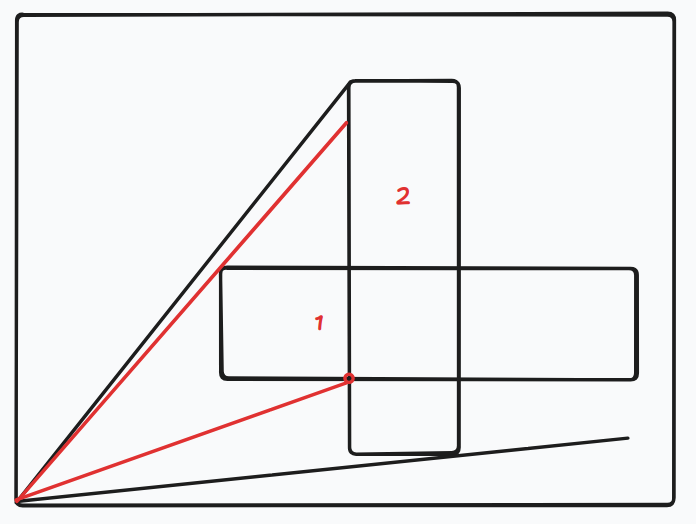
可以看到，2 虽然是后加的，但是红线范围内的答案仍是 1。

我们考虑针对横纵坐标分别开线段树维护其范围内相反坐标的最小值及其序号。简单说，就是对于横坐标的线段树，维护其范围内最小的纵坐标及其序号（答案），纵坐标相同取序号大的，对于纵坐标同理。

每次新增障碍即横坐标线段树增加长方形下边，纵坐标线段树增加长方形左边；每次询问即查询横坐标和纵坐标的线段树并取优。如何取优？首先对于横纵其中一种答案为 0 的，去另一种即可；否则因为斜率相同，我们取横坐标小的；若都相同则取序号大的即可。

实现起来细节还是挺多的，注意横坐标线段树维护的最小纵坐标和纵坐标线段树维护的最小横坐标需要开 long long，因为这个调了快一个小时。注意比较斜率用交叉相乘法，以及线段树大小开够，其它地方正常 int 和 double 就能过。

点击查看代码

#include<bits/stdc++.h>
#define fo(x, y, z) for(register int (x) = (y); (x) <= (z); (x)++)
#define fu(x, y, z) for(register int (x) = (y); (x) >= (z); (x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{
	char ch = getchar();lx x = 0 , f = 1;
	for(;ch<'0'||ch>'9';ch = getchar()) if(ch == '-') f = -1;
	for(;ch>= '0' && ch<= '9';ch = getchar()) x = (x<<3) + (x<<1) + (ch^48);
	return x*f;
}
#undef lx
#define qr qr()
#define pii pair<int , int>
#define fi first
#define se second
const int Ratio = 0;
const int N = 5e5 + 5;
const int mod = 998244353;
int n, tot;
double k[N << 2];
struct rmm{int op, xa, ya, xb, yb;} q[N];
struct Ans{int ans; ll minn;};
struct Wtree
{
    Ans t[N << 2];
    #define ls (rt << 1)
    #define rs (rt << 1 | 1)
    #define mid ((l + r) >> 1)
    void Wupd(int rt, int l, int r, int x, int y, int id, int minn)
    {
        if(x <= l && r <= y)
        {
            if(!t[rt].ans || (t[rt].minn >= minn))
                t[rt].ans = id, t[rt].minn = minn;
            return;
        }
        if(x <= mid) Wupd(ls, l, mid, x, y, id, minn);
        if(y > mid) Wupd(rs, mid + 1, r, x, y, id, minn);
    }
    Ans Wq(int rt, int l, int r, int x)
    {
        if(l == r) return t[rt];
        Ans res;
        if(x <= mid) res = Wq(ls, l, mid, x);
        else res = Wq(rs, mid + 1, r, x);
        if(!t[rt].ans) return res;
        if(!res.ans) return t[rt];
        if(t[rt].minn < res.minn) return t[rt];
        else if(t[rt].minn == res.minn && t[rt].ans > res.ans) return t[rt];
        return res;
    }
} h, s;
namespace Wisadel
{
    double Wget(int x, int y)
    {
        if(x == 0) return 1.0 * 1e18;
        return 1.0 * y / (1.0 * x);
    }
    int Wpk(Ans x, Ans y, int xx, int yy)
    {
        if(!x.ans && !y.ans) return 0;
        if(!x.ans) return y.ans;
        if(!y.ans) return x.ans;
        if(!xx)
        {
            if(q[x.ans].ya < q[y.ans].ya) return x.ans;
            else if(q[x.ans].ya == q[y.ans].ya && x.ans > y.ans) return x.ans;
            return y.ans;
        }
        if(!yy)
        {
            if(q[x.ans].xa < q[y.ans].xa) return x.ans;
            else if(q[x.ans].xa == q[y.ans].xa && x.ans > y.ans) return x.ans;
            return y.ans;
        }
        if(x.minn * xx == y.minn * yy)
        {
            if(x.ans > y.ans) return x.ans;
            return y.ans;
        }
        if(x.minn * xx < y.minn * yy) return x.ans;
        return y.ans;
    }
    short main()
    {
        freopen("raytracing.in", "r", stdin) , freopen("raytracing.out", "w", stdout);
        n = qr;
        fo(i, 1, n)
        {
            q[i].op = qr, q[i].xa = qr, q[i].ya = qr;
            if(q[i].op == 1)
            {
                q[i].xb = qr, q[i].yb = qr;
                k[++tot] = Wget(q[i].xa, q[i].ya);
                k[++tot] = Wget(q[i].xa, q[i].yb);
                k[++tot] = Wget(q[i].xb, q[i].ya);
            }
            else k[++tot] = Wget(q[i].xa, q[i].ya);
        }
        sort(k + 1, k + 1 + tot);
        tot = unique(k + 1, k + 1 + tot) - k - 1;
        fo(i, 1, n)
        {
            if(q[i].op == 1)
            {
                int zs = lower_bound(k + 1, k + 1 + tot, Wget(q[i].xa, q[i].yb)) - k,
                    zx = lower_bound(k + 1, k + 1 + tot, Wget(q[i].xa, q[i].ya)) - k,
                    yx = lower_bound(k + 1, k + 1 + tot, Wget(q[i].xb, q[i].ya)) - k;
                h.Wupd(1, 1, tot, yx, zx, i, q[i].ya);
                s.Wupd(1, 1, tot, zx, zs, i, q[i].xa);
            }
            else
            {
                int kk = lower_bound(k + 1, k + 1 + tot, Wget(q[i].xa, q[i].ya)) - k;
                Ans La = h.Wq(1, 1, tot, kk), Ca = s.Wq(1, 1, tot, kk);
                printf("%d\n", Wpk(La, Ca, q[i].xa, q[i].ya));
            }
        }
        return Ratio;
    }
}
signed main(){return Wisadel::main();}

C. 百鸽笼

学习题面，鸽鸽鸽。

据说是 NOI UNR 的原题。

D. 滑稽树下你和我

有点高级，不过数据很水啊，直接输出起点距离基本上全能过，得亏绑包了。

因为数组范围开小导致少拿了 15pts。

末

挂挂挂挂挂挂挂。

挂了 75pts，跟得的一样多。

虽然开场再次被 T1 硬控后果断选择看后面的题，结果发现甚至都不如 T1 可做，于是只得应干 2h T1，结果还因为唐错没 AC。

开场原题，梦回 T1 3100 高光时刻，然后就罚坐 20min 后换来了这套高质量模拟赛。

最近挂分越来越多了，必须得重视起来了，虽然有可能是因为昨天 abc 一发罚时没吃导致的。

abc 上青了，cf 打一题摆了回来改 T2。

---

完结撒花~