$KMP$学习记

《不浪漫罪名》——王杰

没有花
这刹那被破坏吗
无野火都会温暖吗
无烟花一起庆祝好吗
若爱恋
仿似戏剧那样假
如布景一切都美化
连相拥都参照主角吗
你说我未能定时
令你每天欢笑一次
我没说出一句美丽台词
是你心中一种缺陷定义
流进了眼角里的刺
为何不浪漫亦是罪名
为何不轰烈是件坏事情
从来未察觉我每个动作
没有声都有爱你的铁证
为何苦不浪漫亦是罪名
为何总等待着特别事情
从来未察觉我语气动听
在我呼吸声早已说明
什么都会用一生保证

---

KMP学习记

时更。

---

关于前缀

一个在\(kmp\,\)中较重要的思想。

定义：

一个长度为\(n\,\)的字符串，它的前缀为$$s_1,s_1s_2,···,s_1s_2 ······s_n $$

后缀同理。

真前/后缀即去掉原字符串其他的前缀。

对于一个字符串，它的前缀函数\(\pi [i]\)为\(s_1···s_i\,\)中最长的相等的真前缀和真后缀的长度。

例abcabd（下标从1开始）

\(\pi[1]=0\)；

\(\pi[2]=0\)；

\(\pi[3]=0\)；

\(\pi[4]=1\,\)，a与a；

\(\pi[5]=2\,\)，ab与ab；

\(\pi[6]=0\)。

求解：

暴力做法，复杂度\(O(n^3)\):

for(int i=2;i<=len;i++)
{
	for(int j=i;j>=1;j--)
	{
		if(s.substr(0,j)==s.substr(i-j+1,j))
		{
			pi[i]=j;
			break;
		}
	}
}

优化

摆了，贴上JD的博客

例题

• \(Seek\,the\,Name,\,Seek\,the\,Fame\)

输出该串的所有\(\pi\)函数。

一切仍如昨日所见

#include <bits/stdc++.h>
const int Ratio=0; 
const int N=400005;
int kmp[N],ans[N],cnt,len;
char a[N];
namespace Acheron
{
	void Awork()
	{
		while(std::cin>>a)
		{
			len=strlen(a);cnt=0;
			for(int i=1;i<len;i++)
			{
				int j=kmp[i-1];
				while(j&&a[i]!=a[j])
					j=kmp[j-1];
				if(a[i]==a[j])
					j++;
				kmp[i]=j;
			}
			while(kmp[len-1])
				ans[++cnt]=kmp[len-1],kmp[len-1]=kmp[kmp[len-1]-1];
			for(int i=cnt;i>=1;i--)
				printf("%d ",ans[i]);
			printf("%d\n",len);
		}
	}
}
int main()
{
	Acheron::Awork();
	return Ratio;
}

• 动物\(_{_{洛谷}}\)园\(_{tg}\)

上一张思路图

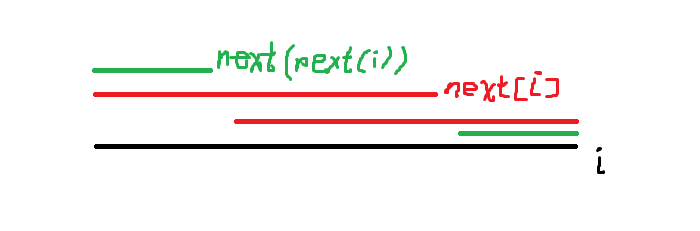
其中，\(next[i]\)，\(next[next[i]]\)，\(next[next[next[i]]]······\)都是这个前缀串i的公共前后缀，而且只有它们是公共前后缀。

那么，我们只要在求\(next\)的过程中，顺便把这个公共前后缀的数量递推一下，就得到了一个弱化版的\(num\)数组：可以重叠的公共前后缀数量。

\(next\)数组的性质之一：\(next[i]<i\)

也就是说，当\(next\)递归至比原前缀i的长度的一半要小时，那么这个\(next\)的递推出的答案\(ans\)就是\(i\)的\(num\)值了。

谨慎，但也无需胆怯

#include<bits/stdc++.h>
#define fo(x,y,z) for(register int (x)=(y);(x)<=(z);(x)++)
#define fu(x,y,z) for(register int (x)=(y);(x)>=(z);(x)--)
typedef long long ll;
typedef unsigned long long ull;
namespace Aventurine
{//快读 快写 快换行、空格输出
	inline ull qr()
	{
		char ch=getchar();ull x=0,f=1;
		for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
		for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<3)+(x<<1)+(ch^48);
		return x*f;
	}
	inline void qw(int x)
	{
		if(!x)
			return;
		qw(x/10);
		putchar(x%10+'0');
	}
	inline void qhh(int x)
	{
		qw(x);
		putchar('\n');
	}
	inline void qkg(int x)
	{
		if(x==0)
			putchar('0');
		else 
			qw(x);
		putchar(' ');
	}
}
using namespace std;
using namespace Aventurine;
#define qr qr()
const int Ratio=0;
const int N=1000005;
const int maxi=INT_MAX;
const ll mod=1e9+7;
char a[N];
int len,kmp[N],ans[N];
ll cnt;
namespace Acheron
{
	void Akmpprepare()
	{
		int j=0;
		ans[0]=0,ans[1]=1;
		fo(i,2,len)
		{
			while(j&&a[i]!=a[j+1])
				j=kmp[j];
			if(a[i]==a[j+1])
				j++;
			kmp[i]=j;
			ans[i]=ans[j]+1; 
		}
	}
	void Awork()
	{
		int j=0;
		fo(i,2,len)
		{
			while(j&&a[i]!=a[j+1])
				j=kmp[j];
			if(a[i]==a[j+1])
				j++;
			while((j<<1)>i)
				j=kmp[j];
			cnt=(cnt*(ll)(ans[j]+1))%mod; 
		}
	}
	void Aput()
	{
		printf("%lld\n",cnt);
	}
}
int main()
{
	int T=qr;
	while(T--)
	{
		scanf("%s",a+1);
		len=strlen(a+1);
		cnt=1;
		Acheron::Akmpprepare();
		Acheron::Awork();
		Acheron::Aput();
	}
	return Ratio;
}

KMP

• 板子题

思路

KMP的精髓在于，对于每次失配之后，我们不会从头重新开始枚举，而是根据我们已知的数据，从某个特定的位置开始匹配。

而对于模式串的每一位，都有唯一的特定变化位置，这个在失配之后的特定变化位置可以帮助我们利用已有的数据不用从头匹配，从而节约时间。

具体例子可以自己手搓一个。

两个关键点：

1.我们的失配数组应当建立在模式串意义下，而不是文本串意义下。因为显然模式串要更加灵活，在失配后换位时，可以更灵活简便地处理。

2.移位法则：在模式串\(s\)中，对于每一位\(si\) ,它的\(kmp\)数组应当是记录一个位置 \(j\)，\(j \leq i\)并且满足\(s_i=s_j\)，并且在\(j!=1\)时满足\(s_1\)至\(s_{j-1}\)分别与\(s_{i-j+1}\)~\(s_{i-1}\)按位相等。

代码

const int Ratio=0;
const int N=1000005;
char a[N],b[N];
int lena,lenb,kmp[N];
namespace Acheron
{
	void Akmpprepare()
	{//kmp-即失配回跳到哪个位置的数组-初始化 
		int j=0;
		fo(i,2,lenb)
		{
			while(j&&b[i]!=b[j+1])//模式串自配 判0：回跳到头 
				j=kmp[j];
			if(b[j+1]==b[i])
				j++; 
			kmp[i]=j;
		}
	}
	void Akmpwork()
	{
		int j=0;
		fo(i,1,lena)
		{
			while(j>0&&b[j+1]!=a[i])//失配回跳 
				j=kmp[j];
			if(b[j+1]==a[i])//匹配成功：对应模式串位置+1 
				j++;
			if(j==lenb)
			{
				printf("%d\n",i-lenb+1);
				j=kmp[j];
			}
		}
	}
	void Aput()
	{
		fo(i,1,lenb)
			qkg(kmp[i]);
	}
}
int main()
{
	scanf("%s%s",a+1,b+1);
	lena=strlen(a+1),lenb=strlen(b+1);
	Acheron::Akmpprepare();
	Acheron::Akmpwork();
	Acheron::Aput();
	return Ratio;
}

• \(Cens_{洛谷}\) \(oring_{tg}\)

思路

关键点在于想出能将删去后的字符串拼接在一起而且能继续匹配的方法...

对了，用\(\huge{栈}\)。

先正常跑一遍\(KMP\,\)板子，然后每次匹配时记录下在\(a_i\)失配时回跳到的下标\(akmp_i\)，当\(j=lenb\)，即模式串被完全匹配后，删除栈内\(lenb\)个元素，将\(j\)回跳，最后反向输出栈内元素（原因是从站内取的总是最新放入，即最后的元素；因此我们可以使用双端队列优化）。

注意！

一个例子：\(a\)串为danhengyinyue，\(b\)串为danheng时，完全匹配后栈内没有元素了，这时候应将\(j\)回跳至\(0\)，代码表示应为：

if(s.size())
	j=akmp[s.top()];
else
	j=0;

因为这个被卡掉12pts的我。。。

霄龙现影，破！

const int Ratio=0;
const int N=1000005;
char a[N],b[N],ans[N];
int lena,lenb;
int kmp[N],akmp[N];
std::stack<int>s;
namespace Acheron
{
	void Aprepare()
	{
		int j=0;
		fo(i,2,lenb)
		{
			while(j&&b[i]!=b[j+1])
				j=kmp[j];
			if(b[j+1]==b[i])
				j++;
			kmp[i]=j;
		}
	}
	void Awork()
	{
		int j=0;
		fo(i,1,lena)
		{
			while(j&&a[i]!=b[j+1])
				j=kmp[j];
			if(a[i]==b[j+1])
				j++;
			akmp[i]=j;
			s.push(i);
			if(j==lenb)
			{
				fo(i,1,lenb)
					s.pop();
				if(s.size()) 
					j=akmp[s.top()];
				else
					j=0;
			}
		}
	}
	void Aput()
	{
		int siz=s.size();
		fo(i,1,siz)
			ans[i]=a[s.top()],s.pop();
		fu(i,siz,1)
			printf("%c",ans[i]);
	}
}
int main()
{
	scanf("%s%s",a+1,b+1);
	lena=strlen(a+1),lenb=strlen(b+1);
	Acheron::Aprepare();
	Acheron::Awork();
	Acheron::Aput();
	return Ratio;
}

---

$Updating...$