动态规划算法学习总结
Interval Scheduling 问题
-
如下图所示,每个长条方块代表一个工作,总有若干个工作a、b... h,横坐标是时间,方块的起点和终点分别代表这个工作的起始时间和结束时间。
-
当两个工作的工作时间没有交叉,即两个方块不重叠时,表示这两个工作是兼容的(compatible)。
-
当给每个工作赋权值都为1时,则称为 Unweighted Interval Scheduling 问题;当给每个工作赋不同的正权值时,则称为 Weighted Interval Scheduling 问题。
-
问题最终是要找到一个工作子集,集合内所有工作权值之和最大且集合内每个工作都兼容。
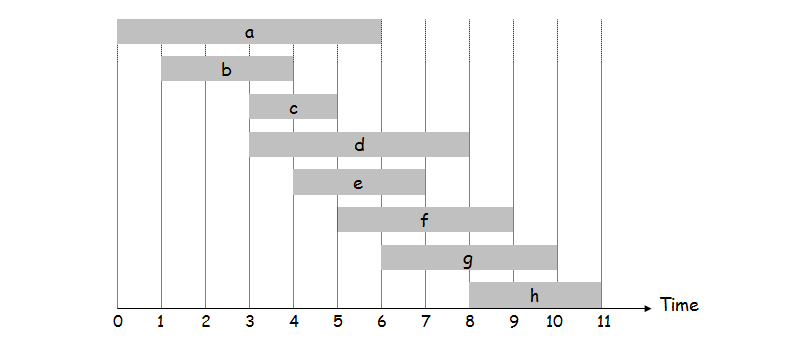
对于 Unweighted Interval Scheduling 问题,使用贪心算法即可求解,具体做法是按照结束时间对所有工作进行排序,然后从结束最晚的工作开始,依次排除掉与前一个不兼容的工作,剩下的工作所组成的集合即为所求。
然而,对于 Weighted Interval Scheduling 问题,贪心法找到的解可能不是最优的了。此时考虑使用动态规划算法解决问题,兼顾权值选择和兼容关系。
定义P(j)
1、首先依然按照结束时间对所有的工作进行排序;
2、定义p(j)为在工作j之前,且与j兼容的工作的最大标号,通过分析每个工作的起始时间和结束时间,可以很容易计算出p(j);
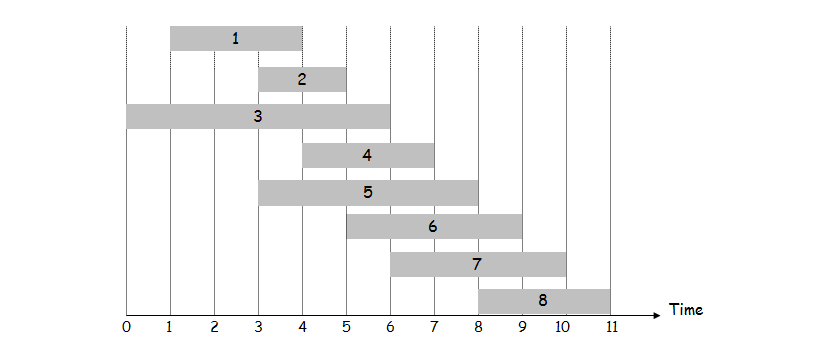
3、例如下图所示,p(8)=5,因为工作7和6都与8不兼容,工作1到5都与8兼容,而5是其中索引最大的一个,所以p(8)=5。同理,p(7)=3,p(2)=0。
分析递归关系
1、定义opt(j)是j个工作中,所能选择到的最佳方案,即opt(j)是最大的权值和;
2、对于第j个工作,有两种情况:
- case 1: 工作j包含在最优解当中,那么往前递推一步,j之前能选择到的最优解是opt(p(j)),即

- case 2: 工作j不在最优解中,那么从j个工作中选取解集和从j-1个工作中选取解集是一样的,即
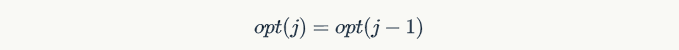
3、当j=0时,显示结果为0,这是边界条件。
后一步的结果取前一步所有可能情况的最大值,因此综上所述,能得到动态规划的递归关系为:

代码实现
1、递归法

递归会使得空间复杂度变高,一般不建议使用。
2、自底向上法

从小到大进行计算,这样每次都可以利用前一步计算好的值来计算后一步的值,算法时间复杂度为O(nlogn),其中排序花费O(nlogn),后面的循环花费O(n)。
Knapsack Problem 问题
背包问题的定义
- 如下图所示,给定一个背包Knapsack,有若干物品Item
- 每个item有自己的重量weight,对应一个价值value
- 背包的总重量限定为W
- 目标是填充背包,在不超重的情况下,使背包内物品总重量最大。
对于下图的例子,一种常见的贪心思想是:在背包可以装得下的情况下,尽可能选择价值更高的物品。那么当背包容量是W=11时,先选择item5,再选择item2,最后只能放下item1,总价值为28+6+1=35。实际上最优解是选择item3和item4,价值18+22=40。这说明了贪心算法对于背包问题的求解可能不是zuiyou的。下面考虑使用动态规划算法求解,首先要推导递归关系式。

推导递归关系式
类似于Weighted Interval Scheduling问题,定义opt(i, w)表示在有i个item,且背包剩余容量为w时所能得到的最大价值和。
考虑第i个item,有选和不选两种情况:
- case 1: 如果选择第i个item,则
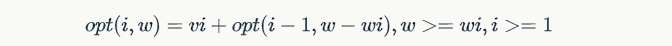
- case 2: 如果不选择第i个item,则
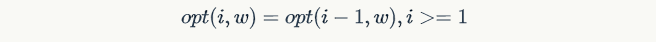
边界条件: 当i=0时,显然opt(i,w)=0。
后一步的结果取前一步所有可能情况的最大值,因此综上所述,能得到动态规划的递归关系为:
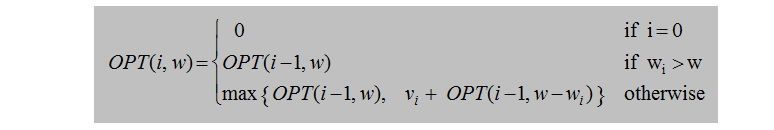
自底向上求解
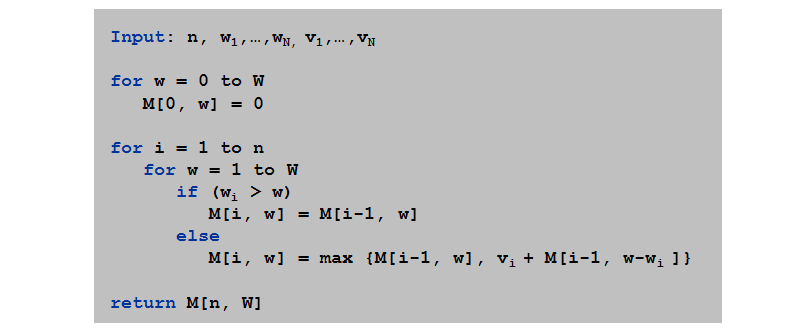
算法迭代过程如下表:
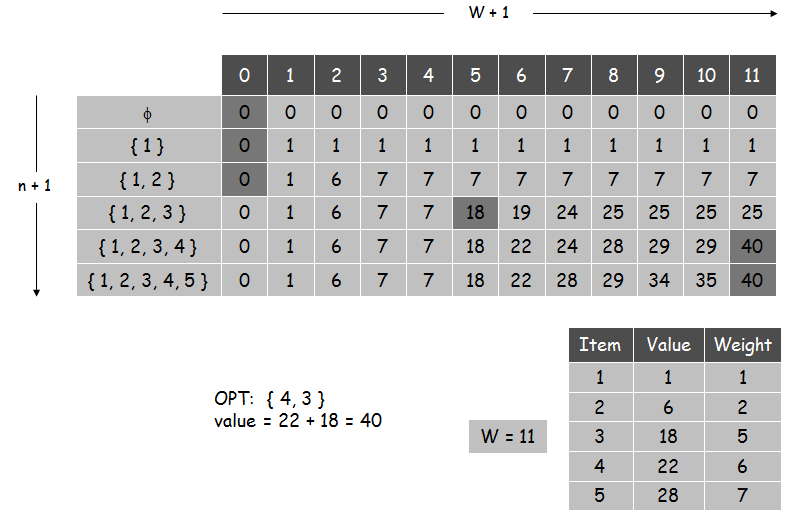
算法运行时间分析

值得注意的是,该算法相对于输入尺寸来说,不是一个多项式算法,虽然O(nW)看起来很像一个多项式解,背包问题实际上是一个NP完全问题。
为了便于理解,可以写成这种形式:

W在计算机中只是一个数字,以长度logW的空间存储,非常小。但是在实际运算中,随着W的改变,需要计算nW次,这是非常大的(相对于logW来说)。例如,当W为5kg的时候,以kg为基准单位,需要计算O(5n)次,当W为5t时,仍然以kg为单位,需要计算O(5000n)次,而在计算机中W的变化量相对很小。
Sequence Alignment
Define edit distance
给定两个序列x1,x2...xi和y1,y2,...,yj。要匹配这两个序列,使相似度足够大。首先需要定义一个表示代价的量-Edit distance,只有优化使这个量最小,就相当于最大化匹配了这两个序列。
Edit distance的定义如下所示。
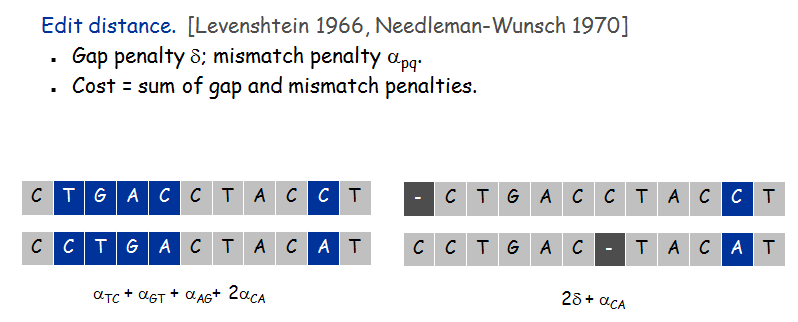
其中,匹配到空,设距离为delta,否则字母p和q匹配的距离记为alpha(p,q),如果p=q,则alpha=0;
那么两个序列匹配的总代价为:

建立递推关系
设opt(i,j)是序列x1,x2...xi和y1,y2,...,yj之间匹配所花费的最小代价。当i,j不全为0时,则分别有三种情况,分别是xi-gap,yj-gap,xi-yj,分别计算不同匹配情况所花费的代价,再加上前一步的结果,就可以建立递推关系式,如下所示。

算法实现

算法复杂度
时间和空间复杂度皆为O(mn)。
下面再分析一个具体的编程问题,使用动态规划算法,但是和上面的DP又有一些区别。
合唱团问题
问题定义
有 n 个学生站成一排,每个学生有一个能力值,牛牛想从这 n 个学生中按照顺序选取 k 名学生,要求相邻两个学生的位置编号的差不超过 d,使得这 k 个学生的能力值的乘积最大,你能返回最大的乘积吗?
输入描述
每个输入包含 1 个测试用例。每个测试数据的第一行包含一个整数 n (1 <= n <= 50),表示学生的个数,接下来的一行,包含 n 个整数,按顺序表示每个学生的能力值 ai(-50 <= ai <= 50)。接下来的一行包含两个整数,k 和 d (1 <= k <= 10, 1 <= d <= 50)。
输出描述
输出一行表示最大的乘积。
问题分析
- 此题的第一个关键点是“要求相邻两个学生的位置编号的差不超过 d”,如果按照传统的DP思路,定义opt(i,k)表示在前i个学生中选取k个学生的最大乘积,建立递推关系:
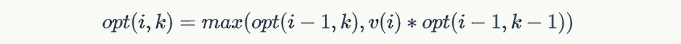
则无法实现“相邻两个学生的位置编号的差不超过 d”的要求。因此,需要定义一个辅助量,来包含对当前学生的定位信息。
- 定义f(i,k)表示在前i个学生中选取k个学生,且第i个学生必选时,所选学生的能力值乘积,这样就包含对当前学生的定位信息,f的递推关系可以表示为
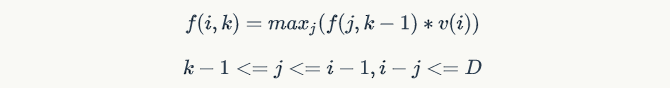
其中,j是一个比i小的值,最大为i-1,i、j之差不超过D,f(j,k-1)表示在前j个学生中,选择k-1个学生,且第j个学生必选。f(i,k)选择了第i个学生,f(j,k-1)选择了第j个学生,i、j之差不超过D,这样就可以满足题目要求了。
- 辅助量f(i,k)并不是我们最终要得到的结果,最终结果opt(i,k)表示在前i个学生中选取k个学生的最大乘积,因此,可以得到opt(i,k)和f(i,k)的关系为:
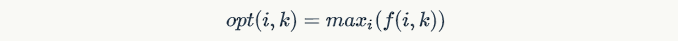
- 该问题的第二个关键点是学生的能力值在-50到+50之间,每次选择的学生的能力值有正有负,所以需要两个f记录最大和最小值,定义fmax和fmin,在每次迭代f的过程中:
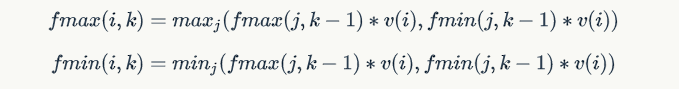
- 当k=K,i=N时,最终所求的:
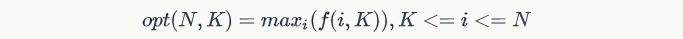
- 边界条件k=1时,f(i,k=1)=v(i)
代码实现
/*********************************************************************
*
* Ran Chen <wychencr@163.com>
*
* Dynamic programming algorithm
*
*********************************************************************/
#include <iostream>
#include <vector>
#include <climits>
#include <algorithm>
using namespace std;
int main()
{
int N, D, K; // 总共N个学生
vector <int> value;
while (cin >> N)
{
for (int i = 0; i < N; ++i)
{
int v;
cin >> v;
value.push_back(v);
}
break;
}
cin >> K; // 选择K个学生
cin >> D; // 相邻被选择学生的序号差值
// fmax/fmin[i, k]表示在选择第i个数的情况下的最大/小乘积
vector <vector <long long>> fmax(N+1, vector <long long> (K+1));
vector <vector <long long>> fmin(N+1, vector <long long> (K+1));
// 边界条件k=1
for (int i = 1; i <= N; ++i)
{
fmax[i][1] = value[i - 1];
fmin[i][1] = value[i - 1];
}
// 自底向上dp, k>=1
for (int k = 2; k <= K; ++k)
{
// i >= k
for (int i = k; i <= N; ++i)
{
// 0 <= j <= i-1 && i - j <= D && j >= k-1
long long *max_j = new long long; *max_j = LLONG_MIN;
long long *min_j = new long long; *min_j = LLONG_MAX;
// f(i, k) = max_j {f(j, k-1) * value(i)}
int j = max(i - D, max(k - 1, 1));
for ( ; j <= i - 1; ++j)
{
*max_j = max(*max_j, max(fmax[j][k - 1] * value[i - 1], fmin[j][k - 1] * value[i - 1]));
*min_j = min(*min_j, min(fmax[j][k - 1] * value[i - 1], fmin[j][k - 1] * value[i - 1]));
}
fmax[i][k] = *max_j;
fmin[i][k] = *min_j;
delete max_j;
delete min_j;
}
}
// opt(N, K) = max_i {f(i, K)}, K <= i <= N
long long *temp = new long long;
*temp = fmax[K][K];
for (int i = K+1; i <= N; ++i)
{
*temp = max(*temp, fmax[i][K]);
}
cout << *temp;
delete temp;
system("pause");
return 0;
}


