机器学习之K均值算法
机器学习的步骤
数据,模型选择,训练,测试,预测
安装机器学习库sklearn
pip list 查看版本 python -m pip install --upgrade pip pip install -U scikit-learn pip uninstall sklearn pip uninstall numpy pip uninstall scipy pip install scipy pip install numpy pip install sklearn
参考网址: https://scikit-learn.org/stable/install.html
导入sklearn的数据集
from sklearn.datasets import load_iris iris = load_iris() iris.keys() X = iris.data # 获得其特征向量 y = iris.target # 获得样本标签 iris.feature_names # 特征名称
K均值算法
K-means是一个反复迭代的过程,算法分为四个步骤:
(x,k,y)
1) 选取数据空间中的K个对象作为初始中心,每个对象代表一个聚类中心;
def initcenter(x, k): kc
2) 对于样本中的数据对象,根据它们与这些聚类中心的欧氏距离,按距离最近的准则将它们分到距离它们最近的聚类中心(最相似)所对应的类;
def nearest(kc, x[i]): j
def xclassify(x, y, kc):y[i]=j
3) 更新聚类中心:将每个类别中所有对象所对应的均值作为该类别的聚类中心,计算目标函数的值;
def kcmean(x, y, kc, k):
4) 判断聚类中心和目标函数的值是否发生改变,若不变,则输出结果,若改变,则返回2)。
while flag:
y = xclassify(x, y, kc)
kc, flag = kcmean(x, y, kc, k)
参考官方文档:
http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html#sklearn.cluster.KMeans
练习
扑克牌手动演练k均值聚类过程:>30张牌,3类
聚类过程如下(这里不演示了,直接进入(2))
初始化
已知数据集合扑克牌(30张牌),及事先指定聚类的总类数(3类),在30张牌中随机选取3个对象作为初始的聚类中心。
设定迭代终止条件
通常设置最大循环次数或者聚类中心的变化误差。
更新样本对象所属类
根据距离准则将数据对象分配到距离最接近的类。
更新类的中心位置
将每一类的平均向量作为下次迭代的聚类中心。
重复步骤3~4,满足步骤2中的迭代终止条件时,停止
自主编写K-means算法 ,以鸢尾花花瓣长度数据做聚类,并用散点图显示。(加分题)
"""
@auther Rakers
@date 2020.04.14
"""
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
# 手动写KMeans聚类算法
def RakersKMeans(data, n_clusters=3):
n = len(data)
k = n_clusters
dist = np.zeros([n, k + 1])
# 设置中心
center = data[:k, :]
center_new = np.zeros([k, data.shape[1]])
number = 0
while True:
for i in range(n):
for j in range(k):
dist[i, j] = np.sqrt(sum((data[i, :] - center[j, :]) ** 2))
dist[i, k] =np.argmin(dist[i, :k]) # 归类
for i in range(k):
index = dist[:, k] == i
center_new[i, :] = np.mean(data[index, :])
if np.all(center == center_new):
break
else:
center = center_new
number += 1
# print('聚类迭代次数', number)
# 调整数字
i = 0
for dd in dist[:, k]:
dist[i, k] = k-1-dd
i+=1
return dist[:, k].astype(np.int32)
if __name__ == "__main__":
# 读取数据
print('获取数据')
iris = load_iris()
data = iris['data']
target = iris['target']
print('获取数据完成')
print('真实类\n', list(target))
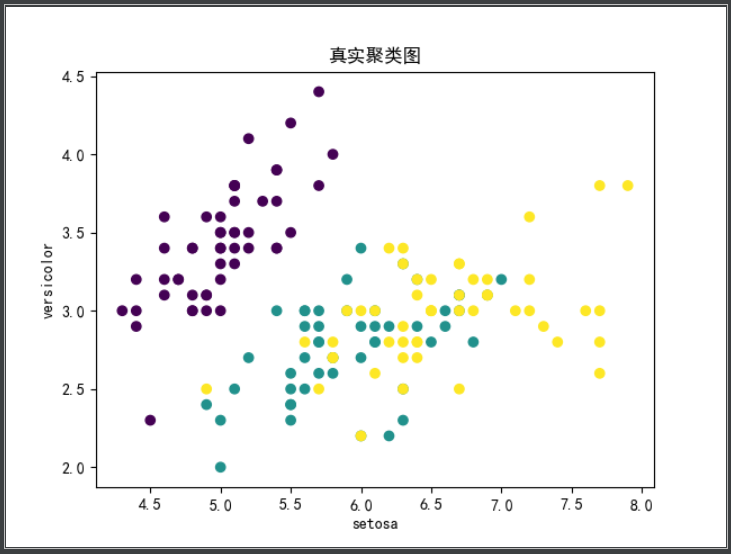
print('真实聚类图')
plt.title('真实聚类图')
plt.scatter(data[:, 0], data[:, 1], c=target)
plt.xlabel(iris['target_names'][0])
plt.ylabel(iris['target_names'][1])
plt.savefig("../images/真实聚类图.png")
print('自主编写K-means算法 ,以鸢尾花花瓣长度数据做聚类')
pre_y = RakersKMeans(data[:, 0].reshape(-1, 1), n_clusters=3)
print('自主编写K-means算法测试类\n', list(pre_y))
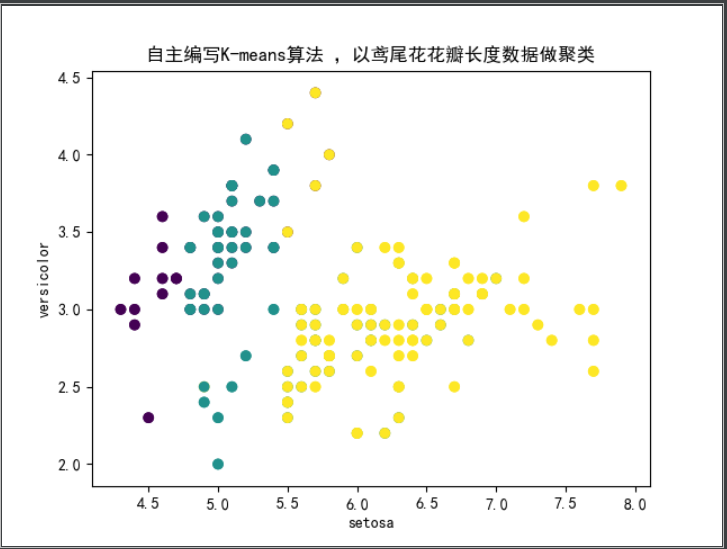
plt.title('自主编写K-means算法 ,以鸢尾花花瓣长度数据做聚类')
plt.scatter(data[:, 0], data[:, 1], c=pre_y)
plt.xlabel(iris['target_names'][0])
plt.ylabel(iris['target_names'][1])
plt.savefig("../images/自主编写K-means算法 ,以鸢尾花花瓣长度数据做聚类.png")
print('用sklearn.cluster.KMeans,鸢尾花花瓣长度数据做聚类')
model = KMeans(n_clusters=3)
model.fit(data[:, 0].reshape(-1, 1))
pre_y = model.predict(data[:, 0].reshape(-1, 1))
print('KMeans算法测试类\n', list(pre_y))
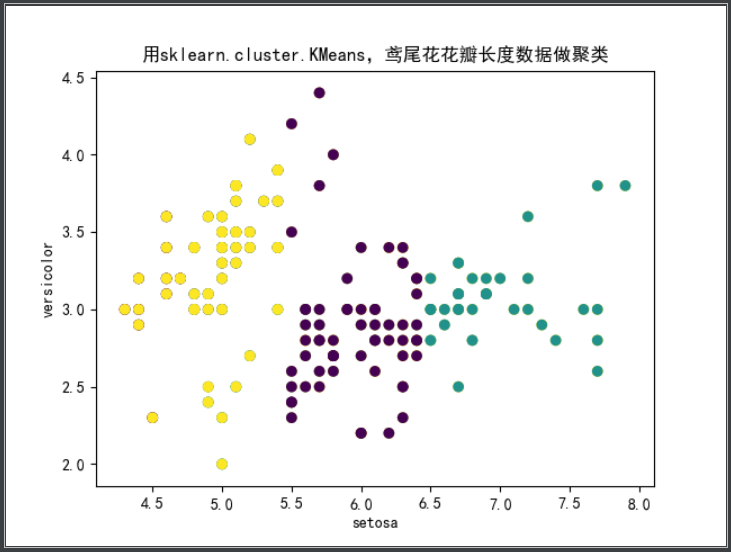
plt.title('用sklearn.cluster.KMeans,鸢尾花花瓣长度数据做聚类')
plt.scatter(data[:, 0], data[:, 1], c=pre_y)
plt.xlabel(iris['target_names'][0])
plt.ylabel(iris['target_names'][1])
plt.savefig("../images/用sklearn.cluster.KMeans,鸢尾花花瓣长度数据做聚类.png")
print('用sklearn.cluster.KMeans,鸢尾花完整数据做聚类')
model = KMeans(n_clusters=3)
model.fit(data)
pre_y = model.predict(data)
print('KMeans算法测试类\n', list(pre_y))
plt.title('用sklearn.cluster.KMeans,鸢尾花完整数据做聚类')
plt.scatter(data[:, 0], data[:, 1], c=pre_y)
plt.xlabel(iris['target_names'][0])
plt.ylabel(iris['target_names'][1])
plt.savefig("../images/用sklearn.cluster.KMeans,鸢尾花完整数据做聚类.png")
真实的聚类效果图
自己编写的K-means算法
用sklearn.cluster.KMeans,鸢尾花花瓣长度数据做聚类,并用散点图显示.
代码同上,这里贴上运行结果
鸢尾花完整数据做聚类并用散点图显示.
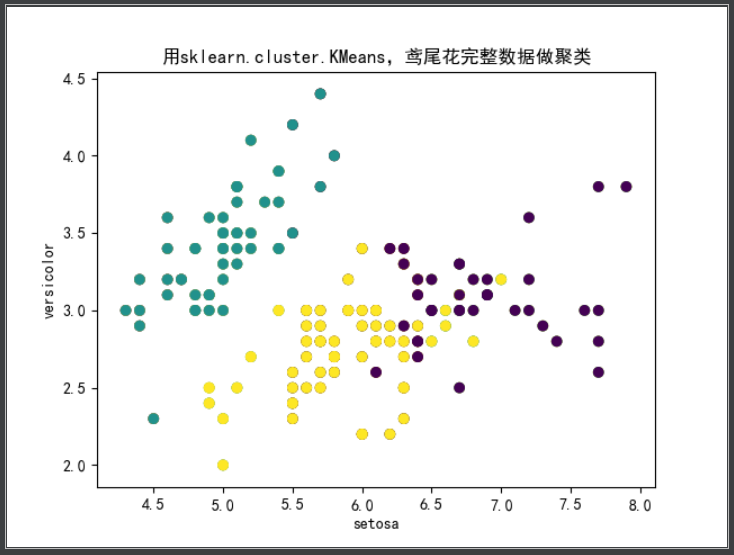
可见当所有的特征都用上时聚类效果与真实的聚类效果最为接近。
想想k均值算法中以用来做什么?
k均值算法是聚类算法,当然最适合用于分类了,像分类图片、文本等,能通过他们的特征,然后把相似的归类到一块,就有类别区分了。


