编译原理之消除左递归
1.将以下文法消除左递归,分析符号串 i*i+i 。
并分别求FIRST集、FOLLOW集,和SELECT集
E -> E+T | T T -> T*F | F F -> (E) | i
消除左递归:
E -> TE' E' -> +TE' | ε T -> FT' T' -> *FT' | ε F -> (E) | i
分析i * i + i:
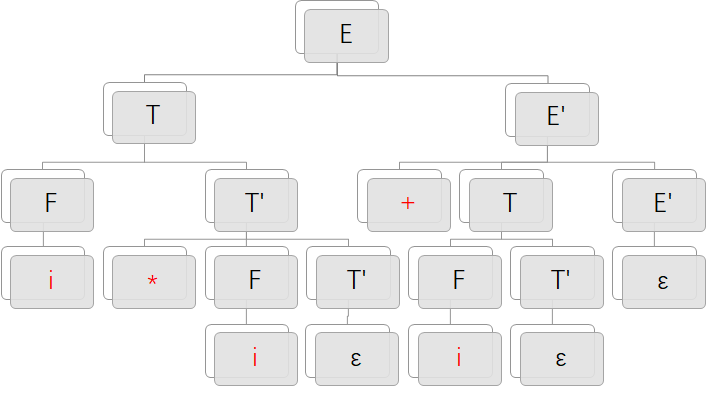
FIRST集:
FIRST(E)=FIRST(T)=FIRST(F)={(,i}
FIRST(E’)= {+,ε}
FIRST(E’)= {+,ε}
FIRST(T’)={*,ε}
FOLLOW集:
FOLLOW(E)={),#}
FOLLOW(E')=FOLLOW(E)={),#}
FOLLOW(T)={+,),#}
FOLLOW(T’)= FOLLOW(T)= {+,),#}
FOLLOW(F)= {+,*,) ,#}
SELECT集:
SELECT(E -> TE')={(,i}
SELECT(E' -> +TE')={+}
SELECT(E' -> ε)={),#}
SELECT(T -> FT')={(,i}
SELECT(T' ->*FT' )={*}
SELECT()={T' ->ε}={+,),#}
SELECT( F -> (E))={(}
SELECT()={F ->i}={i}
2.文法改写,并分别求FIRST集、FOLLOW集,和SELECT集
(1) A -> aABe | a B -> Bb | d (2) S -> Aa | b A -> SB B -> ab
(1)
消除左递归:
A→aA' A'→ABe| ε B→dB' B'→bB' | ε
FIRST(A)={a}
FIRST(A')={a,ε}
FIRST(B)={d}
FIRST(B')={b,ε}
FOLLOW集:
FOLLOW(A)={d,#}
FOLLOW(A')={d,#}
FOLLOW(B)={e}
FOLLOW(B')={e}
SELECT集:
SELECT(A→aA')={a}
SELECT(A'→ABe)={a}
SELECT(A'→ε)={d,#}
SELECT(B→dB')={d}
SELECT(B'→bB')={b}
SELECT(B'→ε)={e}
(2)
消除左递归:
S→bS' S'→BaS' | ε B→ab
FIRST集:
FIRST(S)={b}
FIRST(S')={a,ε}
FIRST(B)={a}
FOLLOW集:
FOLLOW(S)={#}
FOLLOW(S')={#}
FOLLOW(B)={a}
SELECT集:
SELECT(S→bS')={b}
SELECT(S'→BaS' )={a,ε}
SELECT(S'→ ε )={#}
SELECT(B→ab)={a}
课堂练习:
求以下文法的FIRST集、FOLLOW集和SELECT集。
(1)
S -> Ap A -> a |ε A -> cA A -> aA
FIRST集:
FIRST(S)={a,c,p}
FIRST(A)={a}
FIRST(A)={c}
FIRST(A)={a}
FOLLOW集:
FOLLOW(S)={#}
FOLLOW(A)={p}
SELECT集:
SELECT(S->Ap)={a,c,p}
SELECT(A->a)={a}
SELECT(A->ε)={p}
SELECT(A->cA)={c}
SELECT(A->aA)={a}
(2)
S->Ap S->Bq A->a A->cA B->b B->dB
FIRST集:
FIRST(S)={a,c}
FIRST(S)={b,d}
FIRST(A)={a}
FIRST(A)={c}
FIRST(B)={b}
FIRST(B)={d}
FOLLOW集:
FOLLOW(S)={#}
FOLLOW(A)={p}
FOLLOW(B)={q}
SELECT集:
SELECT()={}
SELECT(S->Ap)={a,c}
SELECT(S->Bq)={b,d}
SELECT(A->a)={a}
SELECT(A->cA)={c}
SELECT(B->b)={b}
SELECT(B->dB)={d}


