03/10/2024 上课笔记 & 解题报告
双向链表
前言
第一次接触这玩意儿,所以记录一下。
题目
[国家集训队] 种树
题目描述
A城市有一个巨大的圆形广场,为了绿化环境和净化空气,市政府决定沿圆形广场外圈种一圈树。
园林部门得到指令后,初步规划出 \(n\) 个种树的位置,顺时针编号 \(1\) 到 \(n\)。并且每个位置都有一个美观度 \(A_i\),如果在这里种树就可以得到这 \(A_i\) 的美观度。但由于 \(A\) 城市土壤肥力欠佳,两棵树决不能种在相邻的位置(\(i\) 号位置和 \(i+1\) 号位置叫相邻位置。值得注意的是 \(1\) 号和 \(n\) 号也算相邻位置)。
最终市政府给园林部门提供了 \(m\) 棵树苗并要求全部种上,请你帮忙设计种树方案使得美观度总和最大。如果无法将 \(m\) 棵树苗全部种上,给出无解信息。
输入格式
输入的第一行包含两个正整数 \(n\),\(m\)。
第二行 \(n\) 个整数,第 \(i\) 个代表 \(A_i\)。
输出格式
输出一个整数,表示最佳植树方案可以得到的美观度。如果无解输出 Error!。
样例 #1
样例输入 #1
7 3
1 2 3 4 5 6 7
样例输出 #1
15
样例 #2
样例输入 #2
7 4
1 2 3 4 5 6 7
样例输出 #2
Error!
提示
| 数据编号 | \(n\) 的大小 | 数据编号 | \(n\) 的大小 |
|---|---|---|---|
| \(1\) | \(30\) | \(11\) | \(200\) |
| \(2\) | \(35\) | \(12\) | \(2007\) |
| \(3\) | \(40\) | \(13\) | \(2008\) |
| \(4\) | \(45\) | \(14\) | \(2009\) |
| \(5\) | \(50\) | \(15\) | \(2010\) |
| \(6\) | \(55\) | \(16\) | \(2011\) |
| \(7\) | \(60\) | \(17\) | \(2012\) |
| \(8\) | \(65\) | \(18\) | \(199999\) |
| \(9\) | \(200\) | \(19\) | \(199999\) |
| \(10\) | \(200\) | \(20\) | \(200000\) |
对于全部数据:\(m\le n\),\(-1000\le A_i\le1000\)。
题目分析。
这是一道可反悔贪心 + 双向链表的题。
- 一、可反悔贪心
题目中说,一个树选了旁边两个数就不能选,比如下图。
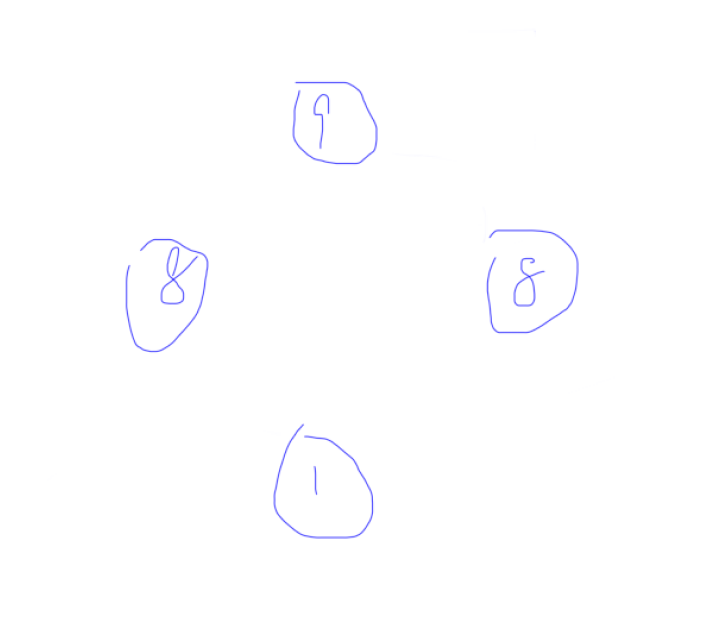
我们肯定先选 \(9\),然后 \(8\)、\(8\) 不能选,所以最后答案是 \(9+1=10\)。但是这题最优解显然是 \(8+8=16\)。
我们肯定会想到用可反悔贪心,用大根堆。
但是我们无法比较,来进行反悔。
于是我们想了一个办法。第一次选 \(9\) 时将 \(8+8-9=7\) 加入这个大根堆。我们不妨来模拟一下。
首先 \(ans\) 加 \(9\),然后删去 \(8\)、\(8\), \(7\) 于队列。
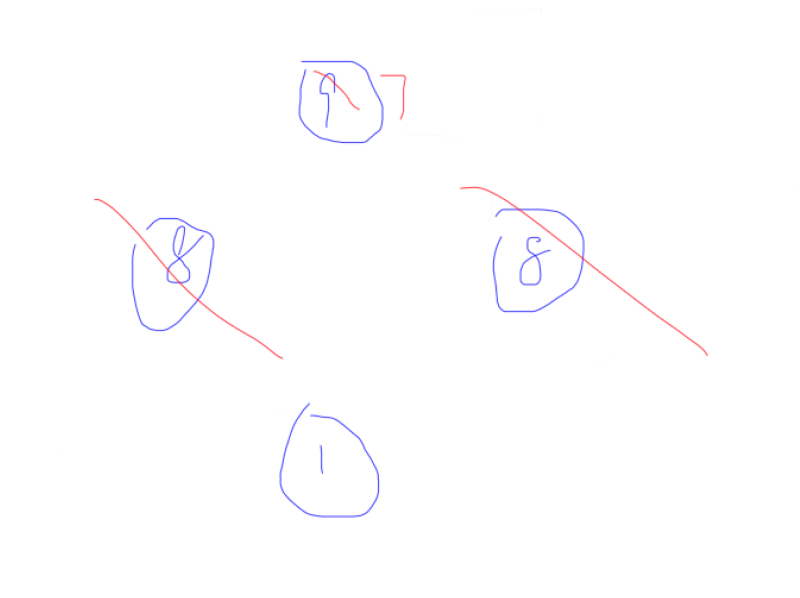
后出 \(8\),被删了,跳过,然后就弹出 \(7\) 了,\(ans\) 加上 \(7\),把两边剔除,
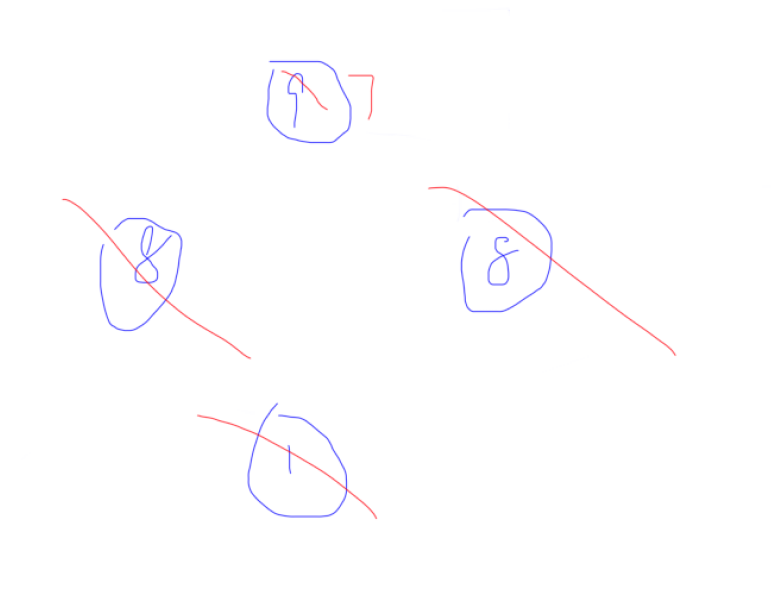
于是答案就是 \(9+7=16\),我们发现和 \(8+8=16\) 结果一样。
- 二、如何用双向链表删点。
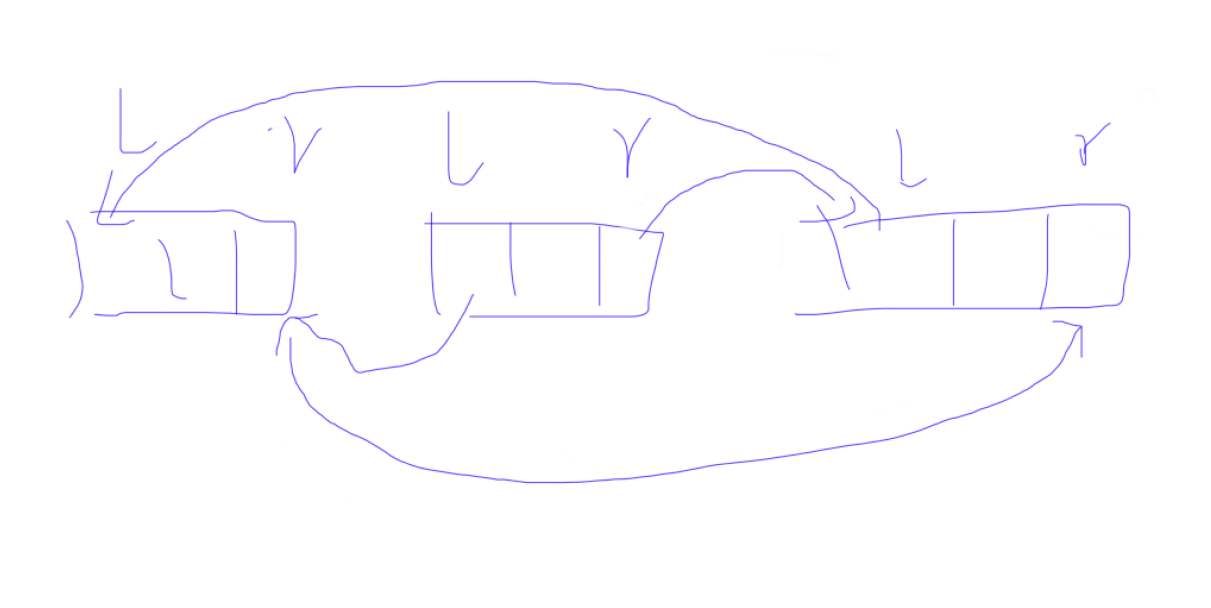
中间的为 \(x\),我们只要让 [p[x].lft].rgt = p[x].rgt,[x].rgt].lft = p[x].lft
然后分别令 \(x\) 为 p[x].lft 和 p[x].rgt` 就行了。
代码
/*
Author: Rainypaster(lhy)
Time: 03/10/2024
File: P1972.cpp
Email: 2795974905@qq.com
*/
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <bits/stdc++.h>
#define int long long
using namespace std;
namespace IO
{
template<typename T>
T read(T x)
{
T sum = 0, opt = 1;
char ch = getchar();
while(!isdigit(ch)) opt = (ch == '-') ? -1 : 1, ch = getchar();
while( isdigit(ch)) sum = (sum << 1) + (sum << 3) + (ch ^ 48), ch = getchar();
return sum * opt;
}
}
#define read IO::read(0)
#define rep(i, n) for(int i = 1; i <= n; i ++)
#define repa(i, n) for(int i = 0; i < n; i ++)
#define repb(i, n) for(int i = 1; i <= n; i ++)
#define repc(i, n) for(int i = 0; i < n; i ++)
#define lson (u << 1)
#define rson (u << 1 | 1)
#define gcd(a, b) __gcd(a, b)
const int N = 2e5 + 5;
struct Node{
int val,id;
bool operator <(Node it) const{
return val < it.val;
}
};
priority_queue<Node> q;
struct node
{
int val, lft, rgt;
}p[N];
bool vis[N];
int ans;
void delt(int x)
{
p[p[x].lft].rgt = p[x].rgt;
p[p[x].rgt].lft = p[x].lft;
}
void solve()
{
int n = read, m = read;
if(n / 2 < m) {
puts("Error!");
return ;
}
for(int i = 1;i <= n;i ++ ){
p[i].val = read;
p[i].lft = i - 1;
p[i].rgt = i + 1;
q.push({p[i].val, i});
}
p[1].lft = n, p[n].rgt = 1;
for(int i = 1;i <= m;i ++ ){
while(vis[q.top().id]) q.pop();
Node now = q.top();
q.pop();
vis[p[now.id].lft] = vis[p[now.id].rgt] = true;
p[now.id].val = p[p[now.id].lft].val + p[p[now.id].rgt].val - p[now.id].val;
ans += now.val;
q.push({p[now.id].val, now.id});
delt(p[now.id].lft), delt(p[now.id].rgt);
}
cout << ans << endl;
}
signed main()
{
int T = 1;
while(T -- ) solve();
return 0;
}
根号分治
前言
简单讲一下,比较简单。
题目
哈希冲突
题目背景
众所周知,模数的 hash 会产生冲突。例如,如果模的数 \(p=7\),那么 \(4\) 和 \(11\) 便冲突了。
题目描述
B 君对 hash 冲突很感兴趣。他会给出一个正整数序列 \(\text{value}\)。
自然,B 君会把这些数据存进 hash 池。第 \(\text{value}_k\) 会被存进 \((k \bmod p)\) 这个池。这样就能造成很多冲突。
B 君会给定许多个 \(p\) 和 \(x\),询问在模 \(p\) 时,\(x\) 这个池内 数的总和。
另外,B 君会随时更改 \(\text{value}_k\)。每次更改立即生效。
保证 \({1\leq p<n}\)。
输入格式
第一行,两个正整数 \(n\), \(m\),其中 \(n\) 代表序列长度,\(m\) 代表 B 君的操作次数。
第一行,\(n\) 个正整数,代表初始序列。
接下来 \(m\) 行,首先是一个字符 \(\text{cmd}\),然后是两个整数 \(x,y\)。
-
若 \(\text{cmd}=\text{A}\),则询问在模 \(x\) 时,\(y\) 池内 数的总和。
-
若 \(\text{cmd}=\text{C}\),则将 \(\text{value}_x\) 修改为 \(y\)。
输出格式
对于每个询问输出一个正整数,进行回答。
样例 #1
样例输入 #1
10 5
1 2 3 4 5 6 7 8 9 10
A 2 1
C 1 20
A 3 1
C 5 1
A 5 0
样例输出 #1
25
41
11
提示
样例解释
A 2 1 的答案是 1+3+5+7+9=25。
A 3 1 的答案是 20+4+7+10=41。
A 5 0 的答案是 1+10=11。
数据规模
对于 \(10\%\)的数据,有 \(n\leq 1000\),\(m\leq 1000\)。
对于 \(60\%\) 的数据,有 \(n\leq 100000\),\(m\leq 100000\)。
对于 \(100\%\) 的数据,有 \(n\leq 150000\),\(m\leq 150000\)。
保证所有数据合法,且 \(1\leq \mathrm{value}_i \leq 1000\)。
分析
我们很容易发现,% 的数越小越不好操作,相反,越大的数暴力就能通过。
所以我们不如把 % 的小于 \(\sqrt(n)\) 的数用 \(f_{x, y}\) 表示 \(x\) % 结果为 \(y\) 的数字的和。
时间复杂度为 \(O(n\sqrt(n))\)。比较优秀。
更改只要更改对应 % 的数组的值就行了。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 150005;
int f[450][450];
int a[N];
signed main()
{
int n, m;
cin >> n >> m;
for(int i = 1;i <= n;i ++ ){
cin >> a[i];
}
for(int i = 1;i <= n;i ++ ){
for(int j = 1;j <= sqrt(n);j ++ ) f[j][i % j] += a[i];
}
while(m -- ){
char cmd;
cin >> cmd;
int x, y;
cin >> x >> y;
if(cmd == 'A'){
if(x <= sqrt(n)){
cout << f[x][y] << endl;
}
else{
int ans = 0;
for(int i = y;i <= n;i += x){
ans += a[i];
}
cout << ans << endl;
}
}
else{
for(int i = 1;i <= sqrt(n);i ++ ) f[i ][x % i] += y - a[x];
a[x] = y;
}
}
return 0;
}

