「WC-2023」学习笔记
upd 2023/02/25 Day4 已更新。
在游记里立 flag 是吧。1 月必更新是吧。
这篇四舍五入就是 1 月学习记录了。1 月剩下的杂题可能放 2 月去写。嗯也可能 2 月就退役了。退役了就没后续了这样。
先放前两天。Day3 杂题选讲没给更新后 PPT()。Day4 题我还没写呢(目移)
有链接的标题是提交入口。
「WC2023 Day1」题目选讲
「IOI 2022」最罕见的昆虫
这是一道交互题。
有 \(n\) 只昆虫,第 \(i\) 只昆虫的类型是 \(a_i\),但不知类型。初始昆虫都在机器外,你可以执行如下操作:(1) 将一只机器外的昆虫放进机器 (2) 将一只机器内的昆虫取出机器 (3) 查询当前机器内类型众数的数量 。
你需要求出,\(n\) 只昆虫中,最少的类型出现了几次。
三种操作的最大次数不得超过 \(3n\),\(2 \le n \le 2000\),交互库不自适应。
考虑让机器内的众数始终为 \(1\)。于是以 \(n\) 的代价就知道类型的数量 \(k\)。
接下来二分答案,查询答案是否 \(\ge x\)。依次加入虫子并且维持众数为 \(x\),然后最后判一下在机器内的数量是否为 \(xk\) 即可。如果不是说明还有类型的数量小于 \(x\)。
如何优化?二分的时候考虑去掉部分虫子。如果答案是 \(>x\),那么就意味着全部类型的数量都 \(>x\),那么我们直接舍去机器中的所有虫子,然后接下来的答案统一加上 \(x\) 即可。否则,就舍去机器外的所有虫子,因为对于那些众数 \(\ge x\) 的数即使去掉了外面的数,数量变成了 \(x\) 个,也不影响接下来的答案判定。
加上此优化后可以通过本题。
「CCPC2022 绵阳站 E」Hammer to Fall
有一张 \(n\) 个点,\(m\) 条边的无向图,每个点上初始有一个人。有 \(q\) 天,第 \(i\) 天会袭击点 \(b_i\)。每个人可以在图上以无限的速度行走,但是袭击时必须停留在某个不是袭击点的点上。
问 \(q\) 天结束之后,所有人行走距离之和最小是多少。
保证 \(n, m, q \le 10^5, w \le 10^9\)。
倒着考虑,不妨设 \(f(i,j)\) 表示时刻 \(i\) 的时候在点 \(j\),需要最小代价能活到最后。于是答案为 \(\sum\limits_{i=1}^n f(0,i)\)。转移如下
对于多次修改,考虑根号分治,每个点开个 set。度数小于 \(\sqrt{n}\) 的点,暴力修改;查询的时候再去查询大于 \(\sqrt{n}\) 的点。
复杂度 \(\mathcal{O}(q \sqrt{m \log n})\)。
「CF1707D」Partial Virtual Trees
给定以 \(1\) 为根的树,定义一个点集是虚树当且仅当点集中任意两个点的 \(\text{LCA}\) 同样在点集中。
询问有多少长为 \(k\) 的虚树序列 \(S_1, S_2,\dots, S_k\) 满足 \(S_1 = \{1, 2,\dots, n\}, S_k = \{1\}, S_{i+1} \in S_i\)。
此处 \(\in\) 表示真子集,\(n, k \le 2000\)。
先容斥一下,这样就没有真子集的要求了。问题转化成每次删除若干个点。
删除的过程,为了满足虚树的条件,每次删除一定是先删除到剩下根一颗儿子树。然后删除根,再删除儿子。于是不妨设 \(f(i,j)\) 表示以 \(i\) 为根节点,在 \(j\) 次删完的方案数。于是有:
这大概就是先求出儿子删掉的方案数,然后讨论,根如果是在所有儿子都删后才删,还是保留一个儿子树,先删根然后再删儿子。
前缀和优化一下,就是 \(\mathcal{O}(n^2)\)。
「CCPC2020 秦皇岛站 D」Exam Results
给定 \(n\) 个区域,每个区域形如某个点的左上方 / 左下方 / 右上方 / 右下方。
求最少选择多少区域覆盖整个平面(或无解)。
保证 \(n \le 10^6\)。
分成四组。左上左下右上右下一定至少选一个。可以证明一定存在一个最优解,其中一个对角组(左上右下 / 左下右上)只需要各选一个。
于是可以枚举是那组。然后就剩下来另外两个对角的两块正方形。对于剩下那个对角组,每组先单调排序。
对于恰好选一个的对角组,我们枚举其中一组选哪个,然后剩下的先选最高 / 低的,接着贪心往下选就行了。选完后另一个对角组该选哪个也呼之欲出了。
贪心过程可以倍增优化。复杂度 \(\mathcal{O}(n \log n)\)。
「ptz camp summer 2022 Day3 F」Flower’s Land
给定一棵 \(n\) 个点的树,每个点有点权。对于每个点,求出包含它的大小恰为 \(k\) 的所有子联通块中,最大的权值和。
保证 \(n \le 4 \times 10^4,k \le 3000\)。
因为 \(k\) 比较大,所以背包合并之类的做法是肯定过不去的。
不妨先考虑假设一定包含 \(1\) 的情况。考虑对 dfs 序 DP,按着顺序 DP,先处理出前缀和后缀的信息,每个点只要合并他的前后缀信息即可。
那么基于这个思想,我们点分治。以包含分治中心为根的子连通块 dfs 序上 DP。同上。复杂度 \(\mathcal{O}(nk \log n)\)。
考虑继续优化,如果当前子连通块大小小于 \(k\) 显然可以舍弃。于是复杂度 \(\mathcal{O}(n \log (\dfrac{n}{k}))\)。
「ptz camp summer 2022 Day3 C」Counting Sequence
一个序列 \(a_1,\dots, a_m\) 是好的当且仅当:(1) \(a_i>0\) (2) \(|a_i - a_{i+1}|=1\) (3) \(\sum\limits_{i=1}^{m-1}a_i =n\)。
对于好的序列,定义权值 \(f(a) = \sum\limits_{i=1}^{m-1} [a_i > a_{i+1}]\),求所有好的序列的 \(c^{f(a)}\) 之和。
保证 \(n \le 3\times 10^5\)。
考虑 DP。不妨设 \(f(i,j)\) 表示当前元素和为 \(i\),上一个数为 \(j\),的答案。转移如下:
复杂度 \(\mathcal{O}(n^2)\)。观察一下,发现 \(m\) 和权值不能同时很大。于是考虑分治。不妨设分治大小为 \(S\)。
如果 \(a_i<S\),这个值域就很小,直接做 DP 就行了。
如果 \(a_1>S\),则有 \(m < S\) 所以也不会存在 \(a_i \le 0\) 的情况,所以考虑没有限制的版本,然后 \(a_1=0\) 总和为 \(j\),长度为 \(i\) 的方案和。然后枚举 \(a_1\) 和 \(m\),结果乘上 \(c^{a_1}\) 即可。
复杂度 \(\mathcal{O}(n \sqrt{n})\)。
「JOI Open 2020 T2」黑白点
在一个环上均匀分布 \(2n\) 个点,其中黑白点各 \(n\) 个。你要画 \(n\) 条线段,形成黑白点之间的匹基于配。
请你求出求最大的相交线段对数。
保证 \(n \le 2 \times 10^5\)。
首先注意到最优情况一定不存在以下这个结构,他可以转化。
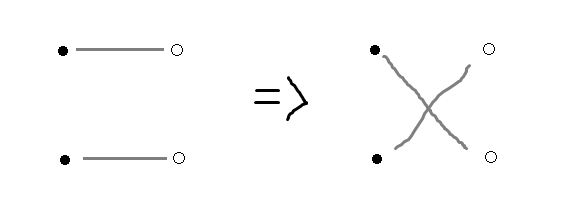
基于这个想法, 考虑构造。最优解一定形如,分别选一个黑点白点作为起点,然后顺时针按顺序连起来。这个可以通过反证法证明。
所以一条线段的交点数就是 \(\min(w_1,b_2)+\min(w_2,b_1)\)。但因为黑点白点数量相等,所以 \(\min(w_1+b_1,w_2+b_2)\)。
双指针即可。复杂度 \(\mathcal{O}(n)\)。
「ICPC2022 济南站 L」Tree Distance
给定一棵带边权的树,每次询问给出一个区间,求:
\[\min\limits_{l \le i < j \le r} \{ \text{dist}(i,j) \} \]保证 \(n \le 2 \times 10^5,1 \le w \le 10^9\)。
考虑点分治,对于一个分治中心 \(u\),我们处理出所有区间内到 \(u\) 的最小值和次小值,然后在这个子连通块中,该区间的答案就是,最小值到 \(u\) 到次小值这个路径。注意到如果选出两个点如果在同一个子树内,这种情况一定会在继续分治下去的过程中被更优的情况覆盖。
所以每次分治的时候可以看成一个序列,求出最小值加次小值。我们可以先处理出每一段的最小值和次小值,然后扫描线求他们的和,但这样更慢了(。
考虑枚举次小值位置 \(x\),这样最小值只需要取两侧最近的小于的数,假设有 \(z<y<x,a_y,a_z \le a_x\),因为我们要满足 \(x\) 是次小值,所以显然 \(y\) 是更优的。
因此对于一个长度为 \(l\) 的序列,可以选出至多 \(2l\) 个关键点。直接扫描线维护就可以了。
「UNR D2T2」神隐
这是一道交互题。
有一棵 \(n\) 个点的树,询问时可以给出 \(\{1,\dots,n-1\}\) 的子集,交互库会返回,连上这些边后,图的联通情况(连通块的集合)。
你需要以任意顺序返回这棵树的所有边。
保证 \(n \le 131072,limit \ge 20\),其中 \(limit\) 表示操作次数限制。交互库不自适应。
考虑把所有边二进制分组。分成 \(0\) 和 \(1\) 两组,两个点在一次查询内连通当且仅当他们之间的边的该位都是 \(0\) 或 \(1\)。
如果两个点在 \(\log\) 次询问都连通,这意味着这两个点是直接相连的。查询次数 \(2 \log n\),复杂度 \(\mathcal{O}(n^2 \log n)\)。
考虑把查询边改成查询点,每个点用 \(2m\) 个位,恰好有 \(m\) 个 \(0\) 和 \(1\) 的二进制编号。然后类似上面的方法查询,操作次数就满足限制了。
不妨先确立出树的拓扑序。叶子等价于恰好有 \(m\) 次都是孤立点。所以每次找叶子删除后继续找,就可以确立拓扑序。
然后确立父亲,对于已经确立的过的点可以打个标记,这样就不用重复判断了。
复杂度 \(\mathcal{O}(n \log n)\)。
「ICPC2022 南京站 L」Proposition Composition
有一条 \(1\) 到 \(n\) 的链,接下来有 \(m\) 次加边操作。
每次加边操作结束后,你需要求出,有多少删除两条边的方式,使得图不连通。
保证 \(n,m \le 2.5 \times 10^5\)。
是一个很神奇的模型转化。
首先找出一个生成树。于是对于非树边,第 \(i\) 条设权值为 \(2^i\)。对于树边,他的权值为所有覆盖他的非树边的权值异或和。
于是可以发现,如果选出两条边的异或和为 \(0\),那么图不连通。否则连通。
考虑用双向链表把本质相同的边串在一起。每次加入一条额外边的时候,就相当于把一些双向链表断开。
但是断开前后缀是不会变的,所以线段树维护一下前后缀,复杂度 \(\mathcal{O}(n \log n)\)。然后再维护一下每次没切的大小就可以了,可以用启发式分裂。
「PR #5」和平共处
平面上有 \(n\) 个黑点,接下来有 \(m\) 个白点依次被加入。对于一对黑白点,如果黑点在白点右上角,那么连一条边。
你需要在每个白点加入后,求出二分图匹配大小。
保证 \(n,m \le 10^5\)。
二分图匹配转成二分图独立集。所以我们只需要画一条左上到右下的折线,因为此时左上白点不可能连上右下角黑点,因此最大化右上角白点和左下角黑点数即可。
因为折线是单调的,所以整体二分的时候,某个时间的决策后,每个点只会在一侧,贡献另一侧。
「WC2023 Day2」网络流在最优化问题中的应用
「Google Code Jam 2022 Round 2」Saving the Jelly
给定平面上 \(n\) 个红点和 \(n + 1\) 个黑点,黑点编号为 \(1\) 到 \(n + 1\)。
每次,你可以选择一个红点,并同时删去它和离它最近的黑点(如果并列,你可以决定删哪一个)。
试构造一种进行 \(n\) 次操作的方案,使得剩下的黑点编号为 \(1\),或报告无解。
保证 \(n \le 10^3\) 坐标范围 \(10^9\)。
可以发现一个红点 \(u\) 能删当且仅当 \(\text{dist}(u,v) \le \text{dist}(u,1)\)。所以依据此建出二分图。如果有解,则一定有完美匹配。
那是否有完美匹配就一定有解?考虑调整法。
对于一个完美匹配,不妨设 \(f(u)\) 表示距离点 \(u\) 的距离比匹配点到 \(u\) 的距离更小的点。然后每次跳 \(f(u)\)。
如果跳到一个 \(f(u)\) 不存在的,就把这跳的过程全部都移到 \(f(u)\) 上。如果跳到一个环,就整体移一位。调整后的完美匹配就是解。
复杂度 \(\mathcal{O}(n^2)\)。
「AGC031E」Snuke the Phantom Thief
在二维平面上,有 \(n\) 颗珠宝,第\(i\)颗珠宝在 \((x_i,y_i)\) 的位置,价值为 \(v_i\)。
现在有一个盗贼想要偷这些珠宝。现在给出 \(m\) 个限制约束偷的珠宝,约束有以下四种:
- 横坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
- 横坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
- 纵坐标小于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
- 纵坐标大于等于 \(a_i\) 的珠宝最多偷 \(b_i\) 颗。
现在问你在满足这些约束的条件下,盗贼偷的珠宝的最大价值和是多少。
保证 \(n\le80,m \le 320,1 \le v_i \le 10^{15}\),坐标范围 \(100\)。
考虑一维的情况。我们把限制转化一下。改成前 / 后 \(k-b_i\) 个珠宝的坐标要小于 \(a_i\)。而 \(k\) 可以枚举。这样我们就得到了每个珠宝的取值范围。暴力连边跑费用流即可。
二维的话差不多。就是把一维的图建两次拼起来。
「HNOI2013」切糕
有一个 \(p \times q \times r\) 的蛋糕,每个点有权值 \(v\)。对于每个纵轴需要选一个点 \(f(x,y)\),且满足 \(|x-x'|+|y+y'|=1\) 的两对点,需要满足 \(|f(x,y)-f(x',y')| \le d\)。
求选出点的权值和最小值。
保证 \(1 \le p,q,r \le 40,0 \le d\le r, \forall v \le 1000\)。
考虑最小割,相当于每个纵轴需要切掉一条边。所以对于所有的 \((x,y)\) 都有 \((x,y,i) \rightarrow (x,y,i+1)\),边权为 \(v_{x,y,i}\)。当然对于 \(i=r\) 的情况可以直接连到大汇点。
考虑那个限制。如果不满足限制,割了等于没割。于是连边 \((x,y,i)\rightarrow (x+1,y,k-d),(x,y,i)\rightarrow (x,y+1,k-d)\)。
求最小割即可。
「CF1630F」Making It Bipartite
图上有 \(n\) 个点,点有点权,点权互不相同,如果两个点点权成倍数关系,那么他们有边。
现在希望删去一些点,来使图变成二分图,求出最少删去多少点。
保证 \(n,a_i \le 5 \times 10^4\)。
我们将偏序关系进行大向小连边,图是二分图当且仅当不存在长度为 \(3\) 的链。所以每个点只有出度或者入度。
因为不能出现连续 \(3\) 个点。所以相当于求独立集。因为图不存在环,也就是说图是一个 DAG,那我们求最大反链即可。
由 Dilworth 定理,我们只需要求最小链覆盖即可。
「AGC029F」Construction of a tree
给定 \(n-1\) 个点集(全集为 \(\{1,2,\ldots,n\}\)),从每个集合内选两个点连边,使得最后形成一棵树。输出方案。
保证 \(n \leq 10^5\),\(\sum |S| \leq 2 \times 10^5\)。
首先,如果 \(n-1\) 条边的图是树的条件是,所有的子集的点大小至少为 \(|S|+1\)。那么考虑充分性。
建图。左侧表示集合,右侧表示点,然后如果包含就连边。跑出来如果匹配为完美匹配,我们从那个没有匹配的点出发跑 dfs,出来的 dfs 序就是这棵树。
如果没有完美匹配。那么一定无解,因为这意味着有 \(2\) 个点是没有匹配的,那么这棵树肯定没法连通。
构造的过程,因为他跑的是增广路,每一个集合相当于都选了非匹配边的点和一个匹配边的点。我们任选一个真子点集,他都一定存在完美匹配,也就意味着他一定满足上面那个条件。得到他的充分性。
「NOI2019」序列
给定序列 \(a_1,\dots,a_n\) 和 \(b_1,\dots,b_n\)。你需要对两个序列分别指定恰好 \(K\) 个下标,使得至少有 \(L\) 个下标在两个序列中都被指定。
最大化指定的 \(2K\) 个下标对应的元素总和。
保证 \(n,K,L \le 2 \times 10^5\),值域 \([1,10^9]\),\(5\) 组数据。
考虑费用流。首先有 \(s \rightarrow a_i\) 流量为 \(1\)(这里表示向 \(a\) 序列第 \(i\) 个连边,下面同理),费用为 \(a_i\) 的权值;\(b_i \rightarrow t\) 流量为 \(1\),费用为 \(b_i\) 的权值。
因为下标不相等最多只能有 \(K-L\) 个,于是连边 \(a_i \rightarrow c \rightarrow d \rightarrow b_j\)。其中 \(c \rightarrow d\) 流量上限为 \(K-L\),其他的为 \(1\),费用均为 \(0\)。
对于剩余的就默认选一致下标的。 那么有 \(a_i \rightarrow b_i\) 流量为 \(1\) 费用为 \(0\)。
这张图的流量为 \(K\) 的最大费用情况就是答案。当然可以多连一条边表示上限为 \(K\)。然后直接跑。
考虑模拟费用流。
逐一加流量。如果 \(c \rightarrow d\) 没满就优先选这条边。这也就是每次在两边各选一个最大值,然后流 \(c \rightarrow d\)。当然如果刚好下标相等就不流这条。
这边满流后,我们可以选 \(a_i + b_i\) 最大的然后流。或者单选一个没选过的 \(a\) 或者 \(b\),然后选另一个下标相同的 \(b\) 或 \(a\),然后这里 \(c \rightarrow d\) 退一流量。
所以我们贪心过程中不需要保证 \(c \rightarrow d\) 是满的,如果出现一对下标相同的情况,可以通过暴力选剩下的最大值让他流满。
用堆维护即可。
「URAL1833」Hope of Rowing
有 \(n\) 个变量 \(x_i \in [0,1]\) 和 \(m\) 个形如 \(x_{u_i} + x_{v_i} \ge 1 (u_i \not= v_i)\) 的约束。
最小化 \(\sum\limits_{i=1}^n x_i\) 并输出方案。
保证 \(n \le 500,m \le 10^5\)。
有一个结论,每个点取值只有 \(0,\frac{1}{2},1\) 三种取值。首先他显然不劣,那么如何证明他不优。假设存在两个点 \(u,v\),他们之间没有约束,但他们各自分别有其他约束 \(u_i,v_j\)。假设 \(u,v > \frac{1}{2},u_i,v_j < \frac{1}{2}\)。发现这情况显然可调整成 \(u,v = 1,u_i,v_j =0\),并且约束情况没变;如果 \(u,v < \frac{1}{2},u_i,v_j > \frac{1}{2}\) 也可以调整。
所以把这每个点拆成两个点表示权值 \(0/1\),对于一个约束 \((u,v)\) 连边 \((u_1,v_2),(u_2,v_1)\)。跑二分图,最后点 \(x\) 的权值就是在匹配中的点取平均值。
「UOJ455」雪灾与外卖
数轴上有 \(n\) 个老鼠和 \(m\) 个洞,第 \(i\) 个洞最多容纳 \(c_i\) 只老鼠。
求让所有老鼠都进洞的最小代价。每只老鼠每移动 \(1\) 的距离会产生 \(1\) 的代价,而第 \(i\) 个洞每容纳一只老鼠会产生 \(w_i\) 的代价。
保证 \(n,m \le 10^5,c_i,w_i \le 10^9\),坐标范围 \(10^9\)。
建图大概就是建一条链,双向的,流量为 \(+\infty\) 费用为 \(1\)。表示走一格的代价。\(s\) 连向有老鼠的点,所有点连向 \(t\),流量上限为 \(c_i\),费用为 \(w_i\)。
洞和老鼠维护堆。里面存代价。从左往右扫就可以知道每个点对应的最小值。
对于一只老鼠,找出一个最小代价的洞钻进去,代价是 \(d+c\)。因为我们是在模拟流量一个一个加的过程,所以如果有退流,那一定是右边的抢占了这老鼠的位置。所以在右边的洞塞一个反悔代价,减去之前花费的同时再减去老鼠的位置 \(-(d+w_i)-d\)。
如果是洞,选择一个老鼠。代价为 \(d+c+w_i\)。反悔同理,选择右边那只,\(-(d+c)-y\)。但因为洞这条边退流后不一定要继续留这条边,所以反悔的时候那个老鼠可以换个洞,老鼠里再塞个 \(-d-c\)。
为了减少重复的代价,可以再记录一个次数值。这样堆内的元素数量就有保证了。
「CF1307G」Cow and Exercise
给出一个 \(n\) 个点 \(m\) 条边的有向图,每条边有边权 \(w_i\)。
有 \(Q\) 次询问,每次询问给出一个 \(x\)。你可以把一条边修改成 \(w_i+a_i\)( \(a_i\) 不一定是整数),不过需要保证 \(a_i \ge 0\) 且 \(\sum a_i<x\)。
你要通过修改边权使得从 \(1\) 到 \(n\) 的最短路径尽可能长,每次询问之间独立。
数据保证至少存在一条从 \(1\) 到 \(n\) 的路径,无重边自环。
首先我们会想到,每次修改 \(1\) 到 \(n\) 的每组路径的必经之路一定最优。也就是修改最小割。
于是把经过同一个最小割的路径归为一个路径集。
因为要使最短路径最长,我们对于一个 \(x\) ,修改路径集中最小的 \(k\) 条边,并且使他们更改后最短路径一样长即可。假设他们都是 \(L\) ,如果此时又其他路径长度小于 \(L\) ,那肯定是选择修改那些路径集。
考虑 EK 算法,因为每次跑完最短路只会找到一个增广路。
建图时每条边流量为 \(1\) ,费用为 \(w_i\) 。当增光 \(k\) 次后就有流量 \(k\) ,因为这 \(k\) 个路径必然没有交点,就是有 \(k\) 个路径集的最短路。
所以可以把每次增广的结果流量和费用存下来,每组的结果为 \(\dfrac{cost_j+x}{flow_j}\) 。
我们发现这个函数是凸的。假设最优的是 \(k\) ,如果 \(j>k\) 意味着增广了更长的路径,那么结果必然更小。 如果 \(j<k\) ,修改的 \(j\) 个路径会小于 \(k-j\) 个路径的最短路。
于是有答案为 \(\min\{\dfrac{cost_j+x}{flow_j}\}\) 。
「WC2023 Day2」欧洲信息学竞赛题目选讲
「PO-Final 2022」三角形演讲
有 \(n\) 个人,每个人有一个权值 \(a_i\)。将他们分成 \(3\) 组,使得第 \(i\) 组的 \(\max \{ a_j \}\) 均大于第 \(i+1\) 组的人数。若 \(i=3\) 则下一组为 \(1\)。
需要判断是否有解。若有解则构造。
满足 \(n \le 5 \times 10^5, 1 \le a_i \le n\)。
首先显然一定存在一组的最大值是全局最大值。不妨设他为第一组,令 \(b_i\) 表示第 \(i\) 组最大值,\(s_i\) 表示大小。
于是接着考虑枚举第二组的最大值,然后对于第三组,我们贪心的希望他的最大值尽量小。
那么我们把 \(a_i\) 排序,然后从小到大一个一个塞进第三组,直到第三组 \(s_3=b_2\)。接着转身去塞第二组,在保持第二组最大值不变的情况下,一个一个塞数直到 \(s_2=b_1\)。然后再把剩下的全部扔第一组。
如果塞不满,那就是不合法。
「EGOI 2022」玩具设计
见 EGOI2022 day2 校内 vp。??我原来 Day2 没打吗(什么那天请假了那没事了。
「BOI 2022」信息传递
这是一道通信题。
给定一个数 \(x \in [1,n]\)。每次只能发送 \(0\) 或 \(1\),但
收到宇宙射线影响信息传递可能有误。每次发送信息后,会得知实际被收到的信息,保证连续两次发送中至少有一次是正确的。接收方需要根据发送的信息,得知 \(x\) 的具体数值。
保证 \(3 \le n \le 10^9,w_{\max}=100\)。其中 \(w\) 表示发送信息的次数限制。
记一个乱搞做法。
首先有一个自然的想法,先不断的发送 \(1\),如果出现一次被欺骗(即对方接受到一个 \(0\)),那么下一次就传输 \(x\) 的二进制的第一位。然后再不断发送 \(1\),以此类推。
但这样容易被自适应交互器干烂,于是考虑对于 \(x\) 的每一位都随机一个双方都知道的密码串,然后将不断发送 \(1\) 改成不断发送该位的密码串,如果密码串有一位发送错误,下一位就传输 \(x\) 的对应位置。
但这样对于出错率低的情况效率很低,于是再设一个上界,如果到达某上界依然是正确传输,那么下一位就传 \(x\) 的对应位置。
正经做法。
首先先把 \(x\) 传一遍,得到了一个错误的串 \(x'\)。我们把 \(x'\) 中错误的位找出来,然后我们把这些位再传过去,又得到了这些位置的错误串。再去传这两个错误的位置,再传下去。直到 \(n=3\)。
分析一下,首先 \(x\) 有 \(2^{30}\) 种可能,但因为不存在连续的两个错误,所以对于 \(x'\) 错误的位置最多 \(15\) 个。这相当于每次需要传的错误位置个数都会除以 \(2\)。最终可以满足条件。
然后考虑 \(n=3\) 的情况。我手动列举了一遍,如果一个数用 \(3\) 个位置表示是表示不出来的。于是考虑用 \(4\) 个数表示。
对于每个数找出一个串,如果传输过来的数和这个串至少有两位匹配,那么我们就可以确定他可能代表的数。
其中,\(1:0000,2:0110,3:1111\)。可以发现,每次传来一个串都可以排除一个数,所以我们只要做两边就可以知道我们要传的是哪个数。
「RMI 2018」登山者
Alice 和 Bob 要爬的山可以用一列折线表示,最左端和最右端的高度均为 \(0\),中间端点的高度均为正整数。
Alice 从山的左端, Bob 从山的右端开始爬山,且保证在任何时刻,必须处于相同的高度。每次改变爬山方向(向上 / 向下)时的高度分别为 \(h_2, h_3, \dots, h_p\),则爬山的体力值为 \(|h_2 - h_1| + |h_3 - h_2| + \dots + |h_p - h_{p-1}|\)。
求 Alice 和 Bob 为了相遇所需的最小体力值。
保证 \(3 \le n \le 5000,1 \le h_i \le 10^6\)。
首先有一个性质。我们只需要记录其中一个人在端点的,另一个人在端点或者折线的情况。因为如果两个人都在折线上,那么他们接下来一定要走上或走下,直到一个人走到端点。
于是我们记录状态 \((x,y)\) 表示,一个人在第 \(x\) 个人端点,另一个人在第 \(y\) 个折线(若两个人都在端点,一个端点可以取他所在的一条折线上)。
于是对于一个状态 \((x,y)\),都只有向上,向下两种走法的选择,根据这个连边。得到一个点和边均为 \(\mathcal{O}(n^2)\) 的图。
跑 dijkstra,然后对于所有相遇的状态取 \(\min\)。复杂度 \(\mathcal{O}(n^2 \log (n^2))\)。
「EJOI 2022」寻找树根
这是一个交互题。
给定一棵树,保证不是一条链。每次你可以询问一个点集的 \(\operatorname{LCA}\) 的是否在该集合内。需要找出树的根。
保证 \(n \le 500\),询问次数 \(k \le 9\)。
首先把度数为 \(1\) 的点叫做叶子节点。剩余的称作中间点。
如果对于一个点 \(r\),对于所有 \(\{ r,v \}(v\in[1,n])\) 的回答都是 Yes,那么 \(r\) 可以为候选根节点。可以发现,存在一些情况 \(r\) 不只一个,当且仅当根节点是叶子节点时,他和他所连接的唯一那个点均为候选根节点。
另外还可以发现,不是根的候选根节点一定是中间点。因为如果存在多个候选根节点,那么根一定为叶子节点,叶子节点所连的出的那条链下的第一个度数 \(>2\) 的点 \(u\),他的两个子树内任意两个叶子节点的集合的 \(\text{LCA} = u\),询问一定为 No。
那我们首先可以选出所有叶子节点做一次询问,他们的 \(\text{LCA}\) 就是根节点,所以如果该询问为 Yes,则根是叶子节点,由于上面的那个性质,意味着只有一个叶子节点是候选根节点,所以可以二分找出那个唯一点;如果询问为 No,那么只有一个候选根节点,我们对所有中间点进行二分,就可以找到那个点。次数为 \(1+9=10\) 次。
考虑舍弃第一部直接开始找,对于所有点按照度数从小到大排序,然后再二分。二分一个 \(k\),查询前 \(k\) 个的集合。
可以发现,如果是第一种情况,那么最后二分的前 \(k\) 个均为叶子节点;否则就是全部叶子节点和部分中间节点,但因为这种情况叶子节点中不存在候选根节点,所以不影响。
「CEOI 2022」奖品
这是一个交互题。
给出两棵树,均有 \(n\) 个节点,每棵树边都边权,但是初始你并不知道。
给定 \(k\),初始可以选择一个大小为 \(k\) 的点集 \(S\),接着你可以询问 \(q\) 次 \((a,b)\),且 \(a,b \in S\),交互器回答 \((d_1(l_1,a),d_1(l_1,b),d_2(l_2,a),d_2(l_2,b))\),其中 \(d_t(x,y)\) 表示在 \(t\) 号树上节点 \(x\) 和节点 \(y\) 的距离,\(l_t\) 表示 \(t\) 号树上 \(a\) 和 \(b\) 的最近公共祖先。
提问结束后,交互器会给你 \(t\) 个询问 \((u,v)\),且满足 \(u,v \in S\),你需要回答 \((d_1(u,v),d_2(u,v))\)。
保证 \(2 \le k \le 10^5,1 \le t \le \min(k^2,10^5)\)。对于
Subtask 2满足 \(q=2k-2\),剩余均满足 \(q=k-1\)。
注意到 \(q=k-1\)。
不妨设 \(d(x)\) 表示点 \(x\) 到根节点的距离,那么一次询问,就可以得到一个 \(d(x)-d(y)=w\) 的方程。然后就有 \(2k-2\) 个方程,未知数有 \(2k-1\) 个未知数。
但如何取点才能保证集合中的所有节点和他们的 \(\text{LCA}\) 都出现在方程中?
选第一棵树的前序遍历的前 \(k\) 个点。这样第一棵树选出来的 \(\text{LCA}\) 一定都在方程中。于是考虑第二课树怎么提问。
将上述编号按照前序遍历一次排序 \(s_1,\dots,s_k\),然后依次提问 \((s_i,s_{i+1})\)。
接下来,对于每次交互器的询问,求出他们 \(\text{LCA}=r\),答案即为 \(d(u)+d(v)-2d(r)\)。
「OIE 2022」最大公约数
这是一道交互题。
需要猜的数为 \(x,y\),每次你可以询问 \(a,b\),交互器会给出 \(\gcd(|x-a|,|y-b|)\),约定 \(\gcd(0,0)=0\)。
保证 \(1 \le x,y \le 10^{18},-2 \times 10^{18} \le a,b \le 2 \times 10^{18}\)。最多可以询问 \(125\) 次。
首先有 \(\log_2 10^{18} = 60\),所以这个答案肯定是 \(\log\) 级别。
我们将 \(x,y\) 写为二进制。可以先询问 \((0,0),(0,1),(1,0),(1,1)\),然后就确定了最低位,也就是确定了奇偶性。
对于下一位,可以先把上一位减去。具体而言 \((0+a_0,0+b_0),(0+a_0,2+b_0),(2+a_0,0+b_0),(2+a_0,2+b_0)\)。然后一位一位算就能算出来了。\(4 \log = 240\),过不去。
不妨设 \((1,0)\) 的时候是偶数,那进一步判断他是不是 \(4\) 的倍数。如果不是,下一位就舍弃两个 \((1,0),(3,2)\) 就不用询问了,因为一定不是 \(4\) 的倍数。反之如果是,就是另外两个不用。
所以我们每次找出上一位偶数的那个,通过判断他是不是 \(2^{x+1}\) 的倍数,来舍弃两个选择。这样除了第一位都只要询问 \(2\) 次。次数 \(2\log+2\)。
「WC2023 Day4」题目选讲
「IOI 2022」数字电路
给定一颗 \(n\) 个点 \(m\) 个叶子的有根树,\(1\) 为根,叶子的编号为 \(n+1,\dots,n+m\)。每个叶子的权值为 \(0\) 或 \(1\)。非叶子节点,由下面规则确定:
- 对于每一个非叶子节点 \(x\),设其儿子节点数量为 \(c_x\),对该节点选择一个 \(\{1, 2,\dots, c_x\}\) 中的参数,令参数为为 \(l_x\)。
- 照从深到浅的顺序确定非叶子节点的权值,对于非叶子节点 \(x\),如果它的儿子节点中至少有 \(l_x\) 个权值为 \(1\),则其权值确定为 \(1\),否则其权值确定为 \(0\)。
有 \(q\) 次修改,每次给定一段区间 \([l, r]\),翻转编号在 \([n + l, n + r]\) 中的叶子节点的权值。在每次修改后,求出有多少种确定每个非叶子节点参数的方式,使得根节点的权值为 \(1\)。答案对 \(10^9 + 2022\)(不是质数)取模。
保证 \(n,m,q \le 10^5\)。
因为每个点的参数只影响自己的权值。不需要考虑儿子的参数,只需要考虑儿子的权值。所以考虑转化形式。
如果他儿子中有 \(x\) 个是 \(1\),有 \(y\) 个是 \(0\)。那么取值范围 \([1,x+y]\)。选 \([1,x]\) 则自身权值为 \(1\),选 \([x+1,x+y]\) 则自身权值为 \(0\)。这等价于,每个点选择一个儿子并且继承他儿子的权值。
于是根节点的权值最后也一定是由某个叶子节点决定的。不妨设他由叶子 \(i\) 的权值 \(v_i\) 决定,且此决定的方案数为 \(f_i\)。那么答案为 \(\sum f_iv_i\)。而 \(f_i\) 就是根节点到叶子的路上的路径之外所有非叶子节点的儿子数量积。
线段树维护区间取反即可。
「ICPC2022 南京站 C」Fabulous Fungus Frenzy
给一个 \(n \times m\) 的字符矩阵 \(A\),同时给定 \(k\) 个字符矩阵作为模板。可以进行如下两种操作:
- 交换两个相邻字符。
- 选择一个模板矩阵,在 \(A\) 中选择一个与模板矩阵形状相同的矩形,将该矩形内的内容替换为模板中的内容。
给定目标状态,判断是否可以达到目标状态。如果可以同时构造方案。
保证 \(n, m, k \le 20\)。操作次数限制:第一种操作 \(4 \times 10^5\) 次,第二种操作限制 \(400\) 次。
如果不考虑操作限制,由于交换操作,我们可以直接考虑元素,不考虑他的位置。这意味着我们每次可以选出任意 \(xy\) 个元素,替换成模板矩阵的元素。
倒着考虑。操作变成了每次选择一个模板,然后替换成其他字符。考虑把这 \(xy\) 个字符全部变成 \(?\) 字符。也就是可以替代成任何其他字符。这样至多会操作 \(nm\) 次,到最后变成初始字符时就知道 \(?\) 该匹配什么。
考虑交换操作的次数。最坏情况下,一次覆盖操作需要 \(nm\) 个元素移动 \(n+m\) 次,也就是最坏总操作 \(n^2m^2(n+m)\) 次。
但如果一个区域全是 \(?\),下次操作只需要找一个需要替换的字符放进去就行,需要注意的是,这个字符必须出现在这个模板中过。
那么对于一个模板,除了第一次操作,剩下操作都可以选择该模板有的字符,移进来,替换成 \(?\)。这样操作次数就大幅度减少了。
「IOI 2022」囚徒挑战
给定 \(n\)。一个房间内有两个 \([1,n]\) 间的不同正整数 \(A, B\) 以及一个白板。白板上可以记录一个自然数 \(x\),初始 \(x = 0\)。
有 \(500\) 个人依次经过房间,他们需要判断 \(A,B\) 的大小关系。每个人进入房间后只能从 \(A,B\) 中选择一个并观察这个数的值,随后更改白板上的 \(x\) 或者给出正确的大小关系并结束整个过程。
每个人不知道所有人进入房间的顺序,因此所有人策略必须相同且确定性。即必须由当前的 \(x\) 决定选择 \(A,B\) 中的哪一个,由当前 \(x\) 以及观察到的值决定下一步的操作(更新 \(x\) 或得到结果)。
构造能确保正确的策略,策略中使用的最大 \(x\) 不能超过 \(lim\)。保证 \(n \le 5000,lim = 20\)。
二进制从高位往低位传。然后再记录当前到第几位,当前看的数是 A 还是 B,看到的是 \(0\) 还是 \(1\)。这样就是 \(3 \left\lceil \log_2 n \right\rceil-1=38\) 个的。
然后发现,看 A 还是 B 这一位可以省略。因为我们一定是两个数轮流看,那如果当前是奇数位我们看 A,偶数位就看 B。这样我们只需要 26 个。
如果我们采用三进制,只需要 \(24\) 个。又因为两个数一定不同。所以到倒数第二位时直接看最后一位,如果倒数第二位相同,那么最后一位一定会出现一个 \(2\) 或者 \(0\)。可以直接比较大小。这样只要 \(22\) 次。
这种优化的本质就是在讨论当前是最大或者最小的情况。最后发现,当 \(k=3,3,3,3,3,2,2,1\) 最优。
「CODE FESTIVAL 2016 Final J」Neue Spiel
有一个 \(n\times n\) 的网格,可以进行如下操作:
选择 \(4n\) 个边界中的一个,从这个边界向内部推入一个方块。方块可以推动其它方块,但不能将方块推出网格。
给出从每一个边界上推入的次数要求 \(a_1,\dots,a_{4n}\),保证 \(\sum a_i = n^2\)。构造一组满足所有推入次数要求的方案使得操作合法(即操作后网格上正好放满方块),或输出无解。
保证 \(n \le 300\)。
倘若不看数字的话,每次推入方格就是选一个当前方向的第一个空位放进去。
考虑网络流。每个格子可以有四个方向进来,对于 \(4n\) 个边界,从源点连流量为初始次数的边,然后所有格子再练一个流量为 \(1\) 到汇点的边。如果满流则有解。
这样也可以构造出解了,按照拓扑序依次选。如果存在环,则将环上重新排列,就可以消去环。
「CEOI2022」Drawing
给定平面上的 \(n\) 个点,和一棵大小为 \(n\) 的树 \(T\),保证这棵树上每个点的度数至多为 \(3\),树上节点按 \(1\sim n\) 编号。
你需要为平面上的点使用 \(1\sim n\) 的编号重编号之后,对于所有树上的边 \(e=(u,v)\),将平面上的点 \(u\) 和平面上的点 \(v\) 用线段连接后,任意两条线段除了在端点上相交没有其他的相交点。
试构造一组方案,保证一定有解。其中 \(n \le 2 \times 10^5\)。
首先任取一个树根。对于所有点,按照极角序排序。按照子树大小,极角序顺序,划分成若干段。每一段的极角最小的点就是与根相连的儿子。递归往下做。复杂度 \(\mathcal{O}(n^2 \log n)\)。
注意到一个点的度数最多为三,那么我们只需要取出极角序最大和最小的点,前划分一段,后划分一段。
我们考虑每次取出轻儿子,剩下的就是重儿子,这样只会取出 \(\mathcal{O}(n \log n)\) 次。
分治维护即可。复杂度 \(\mathcal{O}(n \log^2 n)\)。
「USACO Open 2022」Hoof and Brain P
给定一张 \(n\) 个点 \(m\) 条边的有向图,A,B 两人进行如下二人博弈:
图上有两枚棋子,棋子不能在同一顶点上。每轮操作 A 选择一枚棋子,B 选择将(第一个人选择的)棋子沿着其所在点的一条出边移动(但不能使得两枚棋子重合)。
如果 B 无法操作,则 A 获胜。如果游戏无限进行下去则 B 获胜。
有 \(q\) 次询问,每次给出棋子的初始位置,求双方最优操作下谁获胜。
保证 \(n,m,q \le 2 \times 10^5\)。
首先,如果一个点的出度为 \(0\),把棋子移动到这个点上 B 一定会输。所以在决策上他一定不会这么移动,直接把点删掉即可。
如果一个点的出度为 \(1\),假设为 \(u \rightarrow v\),如果存在一个棋子在点 \(u\) 上,A 可以通过操作移动到 \(v\) 上。且移动前后博弈等价。如果当前 \(u,v\) 上都有棋子,A 选 \(u\) 后则 B 必输。
考虑把形如 \(u \rightarrow v\) 的两个点合并,上个决策意味着两个棋子不能在同一个点。
操作后的图,保证所有点都满足至少 2 出度,也就是一个点至少连出去 \(2\) 个点。所以无论两个棋子在哪里,都有至少一种可行方案。
因此询问前合并图。询问的时候查询棋子所在是否在同一个点 / 被删掉的点即可。
「JOI Open 2022」放学路
给定一个 \(n\) 个点 \(m\) 条边的带权无向图,问是否存在一条 \(n\) 到 \(1\) 的路径,满足路径长度大于 \(1\) 到 \(n\) 的最短路。
保证 \(n,m \le 2 \times 10^5\)。
考虑转化题意,给边定向。
先求出该图的最短路图。按照最短路的方向,在最短路图上的边为正方向。否则方向为反方向。
于是题意转化为:
给一个 \(n\) 个点 \(m\) 条边的 DAG,给定两点 \(s,t\),保证 DAG 中 \(s\) 没有入边,\(t\) 没有出边。
现在去除边的定向变为无向图,询问是否存在一条 \(s\) 到 \(t\) 的简单路径(无重复点),使得路径上至少有一条边经过方向与原 DAG 定向不同。
如果存在一个点 \(u\),在没定向前的图中,不存在 \(s \rightarrow u \rightarrow t\) 的路径(不重复经过同一条边)那么我们可以直接把这个点删掉。
可以发现,上述操作等价于,连边 \(s \leftrightarrow t\),删去与 \(s,t\) 不在一个点双的点。
然后类似上题,我们继续对度数分类讨论。如果一个点的入度或者出度为 \(0\),那么我们直接走 \(s \rightarrow u \rightarrow t\) 路径即可,因为经过点 \(u\) 一定会经过一条边和原来的定向不同。
如果存在一个点入度和出度均为 \(1\),可以直接删去这个点,把他的前后两个点连起来。
考虑重边。如果该重边的权值全部相等并且为最短路图上的边,直接合并所有边。否则,如果存在一个大于最短路图上的边权的边,就将该边反向。
这些操作后,如果只剩下 \(s \rightarrow t\) 两个点一条边,则无解。否则一定有解,考虑如何证明。
此时除了 \(s,t\) 还会剩下一些点,且度数 \(\ge 3\)。我们取出 \(s \rightarrow t\) 的有向最长路,此时取路径上的一点 \(u\),他除了连向最长路上的点外,一定还会连向外面一个点,假设为 \(p\)。然后再经过一些点连回最长路。如果连回最长路的过程上,存在一个不顺向的边,那我们选这个路径,和剩余最长路的部分路径,就是满足他条件的答案。
如果不存在,假设他连回最长路的点为 \(v\),他一定满足 \(u \rightarrow p \rightarrow v\) 的路径大于 \(u \rightarrow v\) 的路径长。此时 \(p\) 还会连向另一跳路径,然后接在了最长路上的 \(q\) 点。如果 \(q\) 不在 \(u \rightarrow v\) 中间,那么我们有答案形如 \(u \rightarrow v \leftarrow p \rightarrow q\)。
如果在中间,就接着往下考虑,由于需要满足 \(u \rightarrow v \rightarrow p\) 为最长路的性质,在最后 \(p,q\) 在最长路上距离为 \(2\) 的时候一定满足条件。证毕。
「IOI 2022」千岛
给一个 \(n\) 个点 \(m\) 条边的有向图。一个人从 \(s\) 出发在图上沿着边的方向游走,有如下限制:
- 在经过一条边后,它的定向会改变。
- 不能连续两次沿着同一条边走。
- 结束时必须回到起点,且每条边必须经过偶数次。
询问是否存在一条经过至少一条边的合法游走路线。如果存在同时构造一条不超过 \(2\times 10^6\) 条边的方案。
保证 \(n,m \le 2 \times 10^5\)。
首先,不能进过出度为 \(0\) 的点,因为如果一到这个点,就必须立刻返回,且只能返回前面刚走过的边,因为只有他反向了。但这样是不合法的。可以把这样的点先删掉。
如果起点的出度为 \(1\),即 \(s \rightarrow u\),那么我们初始只能从这条边出发,这之后起点的出度变成了 \(0\)。由上句话的讨论可以得知,若我们再次返回起点,就必须结束游戏。且只有返回之前走的那条边才能保证走偶数次。因此,我们可以直接把起点 \(s\) 删去,如果点 \(u\) 出发的路径合法,那么 \(s\) 也合法。
接下来所有点满足,非起点出度 \(\ge 1\),起点出度 \(\ge 2\)。
从起点出发,可以走出一个基环内向森林,对于一个颗树,走完环后,他环上所有边都会反向。但是因为不能连续两次经过一条边,我们接下来就没法继续走这颗基环树了。
但起点的出度满足 \(\ge 2\)。我们考虑一个两个基环树合并的情况。
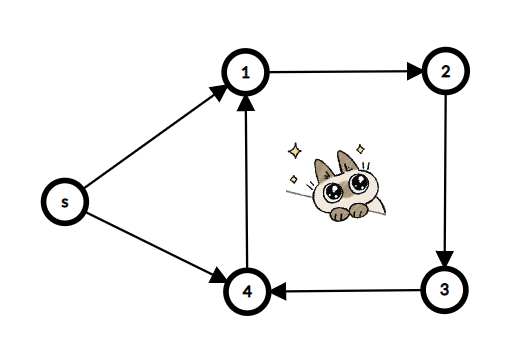
然后就从 \(s\) 两个出发的两条路径分别走一次。具体而言 \(s \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1 \rightarrow s \rightarrow 4 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow 4 \rightarrow s\)。
如果没有重合,就一定没有交。
复杂度 \(\mathcal{O}(n+m)\)。
警钟长鸣
WC 后有一次 vp 打 ACM。有一题也是这个思路,然后我念完题目 18Michael 就秒了然后我还在原地愣了几分钟。
怎么回事呢!!!!!


