「CSP-S 2021」初赛解析

  • 前言

    My blog。

    谢谢，非常自闭，感觉没脸人见了。错一堆傻逼的不该错的。

    写完解析我觉得我更蠢了怎么办。

    感谢同学们的指正！特别感谢 chen_03 帮我指正了亿个错误。

    想要部分题目的博客源码可以私信。

    代码题的代码暂鸽。

  • 选择题

1.在 Linux 系统终端中，用于列出当前目录下所含的文件和子目录的命令为（ ）。

A. ls B. cd C. cp D. all

ls 命令用于显示指定工作目录下之内容（列出目前工作目录所含之文件及子目录)。

cd 命令用于切换当前工作目录。

cp 命令主要用于复制文件或目录。

all 我也不知道这干啥。

故选 A 。

2.二进制数 \(00101010_2\) 和 \(00010110_2\) 的和为（ ）。

A. \(00111100_2\) B. \(01000000_2\) C. \(00111100_2\) D. \(01000010_2\)

计算题，\(1+1=10,0+0=0,1+0=1\) 。

算出来是 \(01000000_2\) 故选 B 。

3.在程序运行过程中，如果递归调用的层数过多，可能会由于（ ）引发错误。

A. 系统分配的栈空间溢出

B. 系统分配的队列空间溢出

C. 系统分配的链表空间溢出

D. 系统分配的堆空间溢出

递归的时候是像栈一样，先进后出的。

故选 A 。

4.以下排序方法中，（ ）是不稳定的。

A. 插入排序 B. 冒泡排序 C. 堆排序 D. 归并排序

补充不稳定是什么：

比如 \(2\) 个值，第 \(x\) 个数字是 \(z\) ，第 \(y\) 个数值也是 \(z\) 。其中不妨设 \(x<y\) 。但是某些不稳定的排序后可能会出现 \(x\) 排到 \(y\) 后面的情况。

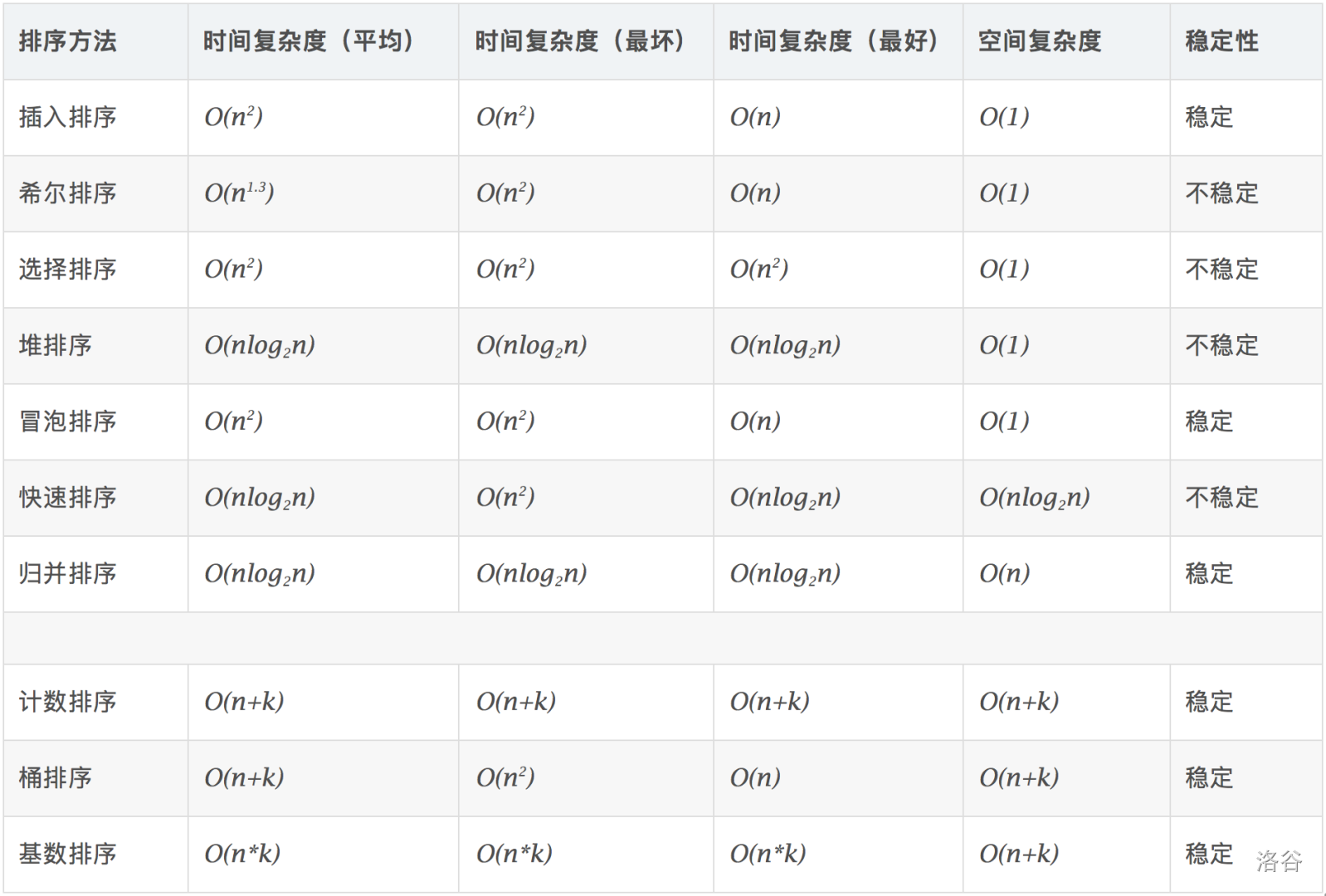
故选 C 。

5.以比较为基本运算，对于 2n 个数，同时找到最大值和最小值，最坏情况下需要的最小的比较次数为（ ）。

A. \(4n-2\) B. \(3n+1\) C. \(3n-2\) D. \(2n+1\)

关于从原题那年就开始理解错这件事。

把序列分成两半，长度分别为 \(n\) 。两两之间比，小的和最小值比，大的和最大值比。其中两组第一个数只要比一次。

所以 \(1+3 \times (n-1)=3n-2\) 。

故选 C 。

6.现有一个地址区间为 \(0\) 到 \(10\) 的哈希表，对于出现冲突情况，会往后找第一个空的地址存储（到 \(10\) 冲突了就从 \(0\) 开始往后），现在要依次存储 \((0,1, 2,3,4,5,6,7)\) ，哈希函数为 \(h(x)=x^2 \bmod 11\) 。请问 7 存储在哈希表哪个地址中（ ）。

A. 5 B. 6 C. 7 D. 8

每个都算一下。分别为 \(0,1,4,9,5,3,3,5\) 。

重复的调整一下 \(0,1,4,9,5,3,6,7\) 。

故选 C 。

7.G 是一个非连通简单无向图（没有自环和重边），共有 36 条边，则该图至少有（ ）个点。

A. 8

B. 9

C. 10

D. 11

设有 \(n\) 个点，除了一个孤立点外剩下点为完全图。

\[\dfrac{1}{2}(n-1)(n-2)=36 \]

解得 \(n=10\)

故选 C 。

8.令根结点的高度为 1，则一棵含有 2021 个结点的二叉树的高度至少为（ ）。

A. 10

B. 11

C. 12

D. 2021

“至少”，故是完全二叉树。

所以 \(2^{10} \le 2021 < 2^{11}\) 。

故选 B 。

  1. 前序遍历和中序遍历相同的二叉树为且仅为（ ）。

A. 只有 1 个点的二叉树

B. 根结点没有左子树的二叉树

C. 非叶子结点只有左子树的二叉树

D. 非叶子结点只有右子树的二叉树

前序遍历：中左右。

中序遍历：左中右。

所以去掉左时两个相同，选择 D 。

10.定义一种字符串操作为交换相邻两个字符。将 \(\mathtt{DACFEB}\)变为 \(\mathtt{ABCDEF}\) 最少需要（ ）次上述操作。

A. 7 B. 8 C. 9 D. 6

考虑冒泡排序思想。

\(\mathtt{ADCFEB}\) 1 次。

\(\mathtt{ABDCFE}\) 4 次。

\(\mathtt{ABCDFE}\) 1 次。

\(\mathtt{ABCDEF}\) 1 次。

共 7 次。

故选 A 。

11.有如下递归代码

solve(t, n):
if t=1 return 1
else return 5 * solve(t-1,n) mod n

则 solve(23,23) 的结果为（ ）。

A. 1

B. 7

C. 12

D. 22

阅读可得，要求 \(5^{23-1} \bmod 23\) 。

考虑用费马小定理，因为 \(23\) 是质数，所以 \(5^{22} \equiv 1 \pmod {23}\) 。

故选 A 。

12.斐波那契数列的定义为： \(F_1=1,F_2=1,F_n=F_{n-1}+F_{n-2} (n \ge 3)\) 。现在用如下程序来计算斐波那契数列的第 n 项，其时间复杂度为（ ）。

F(n):
if n<=2 return 1
else return F(n-1) + F(n-2)

A. \(\mathcal{O}(n)\)

B. \(\mathcal{O}(n^2)\)

C. \(\mathcal{O}(2^n)\)

D. \(\mathcal{O}(n \log n)\)

\(T(n)=T(n-1)+T(n-2)\) ，所以复杂度也是 \(\mathcal{O}(F_n)\) 。

或者说是 \(2^n\) ，因为每一项都是 \(F_n=F_{n-1}+F_{n-2}\) 。

故选 C 。

13.有 8 个苹果从左到右排成一排，你要从中挑选至少一个苹果，并且不能同时挑选相邻的两个苹果，一共有（ ）种方案。

A. 36 B. 48 C. 54 D. 64

是某一年的填空题换了个外套。

选 \(1\) 个苹果，有 \(8\) 种结果。

选 \(2\) 个苹果，可以固定第一个往后，有 \(6+5+4+3+2+1=21\) 种。

选 \(3\) 个苹果，有 \(4+3+2+1+3+2+1+2+1+1=20\) 。

选 \(4\) 个苹果，有 \(5\) 种。

所以总数 \(8+21+20+5=54\) 。

可以换一种方法。

设 \(f_i\) 表示有 \(i\) 个苹果的方案总数（可以不取）。

考虑转移 \(f_i=f_{i-1}+f_{i-2}\) 。

所以 \(f_8=55\) ，答案为 \(f_8-1=54\) 。

故选 C 。

14.设一个三位数 \(n = \overline{abc}\) ，其中 \(a,b,c\) 均为 \(1\) 到 \(9\) 之间的整数，若以 \(a,b,c\) 作为三角形的三条边可以构成等腰三角形（包括等边），则这样的 \(n\) 有（ ）个。

A. 81 B. 120 C. 165 D. 216

考虑 \(a = b \not = c\) 有几种。

\(1,1\) 无解。\(2,2\) 有 \(2+2-1-1=2\) 种。

同理，\(3,3\) 有 \(4\) 种，\(4,4\) 有 \(6\) 种，后面 \(5\) 到 \(9\) 都是 \(8\) 种。

所以 \(8 \times 5 + 6 + 4 + 2=52\) 。

而 \(a=b=c\) 有 \(9\) 种。

所以 \(52 \times 3 + 9 = 165\) 。

故选 C 。

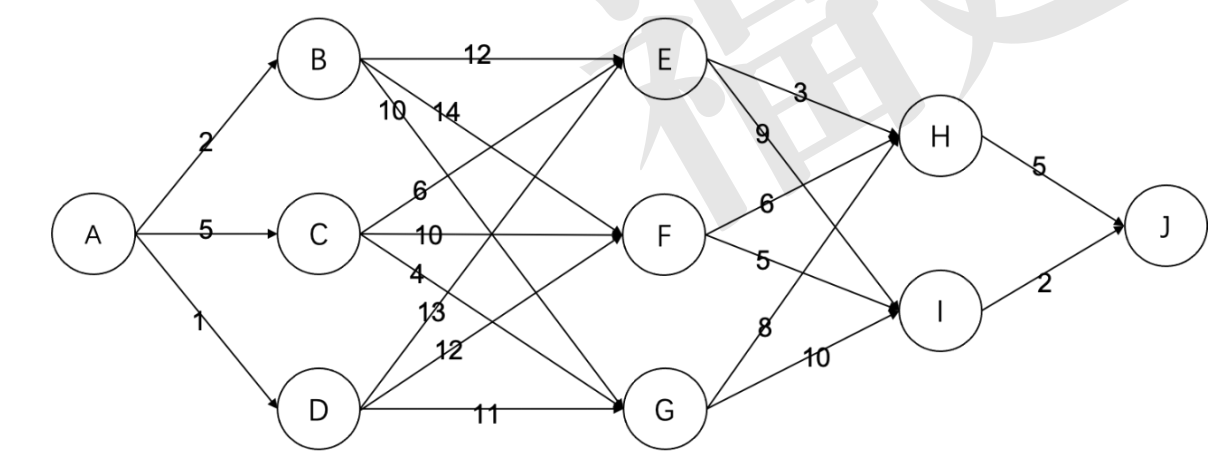
15.有如下的有向图，节点为 A, B, … , J, 其中每条边的长度都标在图中。则节点 A 到节点 J 的最短路径长度为（ ）

A. 16 B. 19 C. 20 D. 22

考虑模拟 dijkstra 。

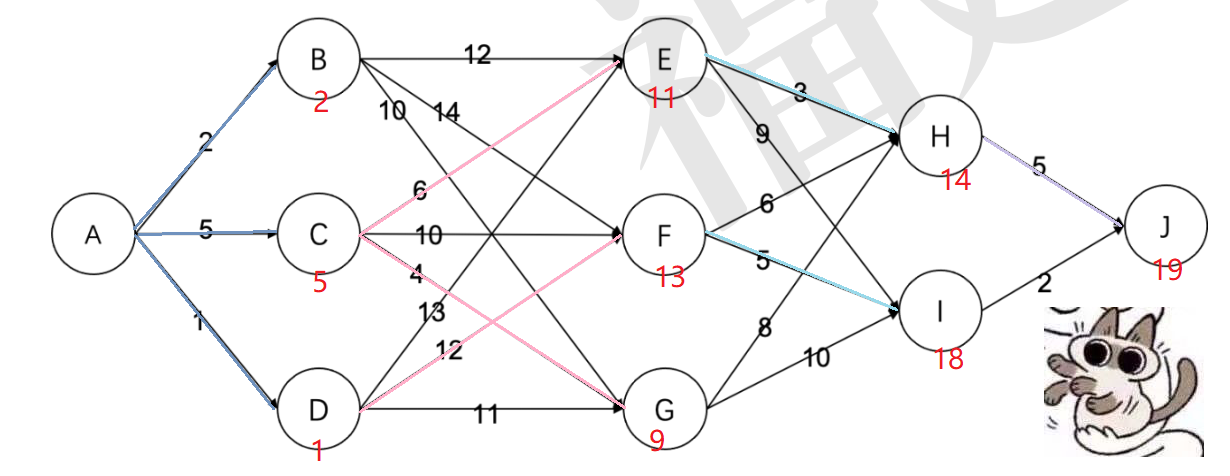
故选 B 。

  • 阅读程序

(1)

首先先看一下程序，通过求 \(t\) 可以猜出这是三维坐标系。还有 \(r\) 可以大致猜测是球。

因为 \(\cos 60^\circ = 0.5\) ，而 \(60^\circ\) 在弧度制下就是 \(\dfrac{\pi}{3}\) 。

可以猜测一下，因为 \(V=\dfrac{4}{3}\pi r^3\) ， \(r\) 是 \(\dfrac{\pi}{3}\) ，所以本题和球关系很大，而 \(d\) 是半径。

16.将第 \(21\) 行中 \(t\) 的类型声明从 int 改为 double ，不会影响程序运行的结果。（ ）

没有任何下取整的操作，并且结果也是 double 不影响。

故判对。

17.将第 26、27 行中的/ sqrt(t) / 2替换为/ 2 / sqrt(t)，不会影响程序运行的结果。（ ）

这里 sqrt 是小数，若先除以 \(2\) 会默认下取整。

故判错。

18.将第 28 行中的x * x改成sq(x)、y * y改成sq(y) ，不会影响程序运行的结果。（ ）

sq() 函数内是算 int 类型的平方，这里的 x 和 y 都是 double 类型。

故判错。

19.（2 分）当输入为0 0 0 1 1 0 0 1时，输出为1.3090。（ ）

手动模拟，这个不会难算。结果为 \(\dfrac{5 \pi }{12}\) 估算一下，差不多。

故判对。

20.当输入为1 1 1 1 1 1 1 2时，输出为（ ）。

A. 3.1416 B. 6.2832 C. 4.7124 D. 4.1888

走特判，所以 \(\dfrac{4}{3}\pi r^3\) 直接带进去，其中 \(r\) 取 \(1\) 。

故选 D 。

21.（2.5 分）这段代码的含义为（ ）。

A. 求圆的面积并 B. 求球的体积并

C. 求球的体积交 D. 求椭球的体积并

根据上面的叭叭，和特判的 min ，所以判断是交。

故选 C 。

(2)

阅读程序后，发现这是在求最大子段和。

先看 solve2 再看 solve1 会更轻松，不过其实把判断题带进去也很好（（

22.程序总是会正常执行并输出两行两个相等的数。（ ）

确实。判对。

23.第 28 行与第 38 行分别有可能执行两次及以上。（ ）

考虑二分到最边界，此时 \((n,n+1)\) 会分成 \((n,n)\) 和 \((n+1,n+1)\) 。

相等情况被特判走了，所以不会走那两行特判。

若开头输入的 \(n<0\) ，也只会分别执行一次。

故判错。

24.当输入为5 -10 11 -9 5 -7时，输出的第二行为“7”。（ ）

需要注意 \(5\) 为 \(n\) （……）。

所以这一段的最大字段和为 \(11\) 。

故判错。

25.solve1(1, n) 的时间复杂度为（ ）。

A. \(\mathcal{O}(\log n)\) B. \(\mathcal{O}(n)\) C. \(\mathcal{O}(n \log n)\) D. \(\mathcal{O}(n!)\)

\(T(n)=2T \left( \dfrac{n}{2} \right) + 1\)

\(T(n)=2n-1\) 故选 B 。

26.solve2(1, n) 的时间复杂度为（ ）。

A. \(\mathcal{O}(\log n)\) B. \(\mathcal{O}(n)\) C. \(\mathcal{O}(n \log n)\) D. \(\mathcal{O}(n!)\)

\(T(n)=2T \left( \dfrac{n}{2} \right) + n\)

\(O(n\log n)\) 故选 C 。

27.当输入为10 -3 2 10 0 -8 9 -4 -5 9 4时，输出的第一行为（ ）。

A. 13 B. 17 C. 24 D. 12

注意 \(10\) 是 \(n\) （草！）。

所以最大字段和为 2 10 0 -8 9 -4 -5 9 4 ，为 \(17\) 。

(3)

粗略扫过去可以发现是加密和解密过程。

28.程序总是先输出一行一个整数，再输出一行一个字符串。（ ）

根据同学的说法，可能因为空串没东西。

空串凭什么不是字符串（恼）。

29.对于任意不含空白字符的字符串 str1，先执行程序输入0 str1，得到输出的第二行记为 str2；再执行程序输入1 str2，输出的第二行必为 str1。（ ）

既然是加密和解密，这两个必然相同。

故判对。

30.当输入为1 SGVsbG93b3JsZA==时，输出的第二行为HelloWorld。（ ）

手动模拟。判错。

31.设输入字符串长度为 n，encode 函数的时间复杂度为（ ）。

A. Θ,\(\mathcal{O}(\sqrt n)\). B. \(\mathcal{O}(n)\) C. \(\mathcal{O}(n \log n)\) D. \(\mathcal{O}(n!)\)

看程序，是 \(\mathcal{O}(n)\) 的。

故选 B 。

32.输出的第一行为（ ）。

A. 0xff B. 255 C. 0xFF D. -1

怎么说，有的人电脑是 -1 有的人是 255 。等最后官方通知。

答案是 D 。

33.（4 分）当输入为0 CSP2021csp时，输出的第二行为（ ）。

A. Q1NQMjAyMWNzcAv= B. Q1NQMjAyMGNzcA==

C. Q1NQMjAyMGNzcAv= D. Q1NQMjAyMWNzcA==

模拟，选 D 。

  • 完善程序

(1)

（魔法数字）小 H 的魔法数字是 \(4\) 。给定 \(n\) ，他希望用若干个 \(4\) 进行若干次加法、减法和整除运算得到 \(n\) 。但由于小 H 计算能力有限，计算过程中只能出现不超过 \(M = 10000\) 的正整数。求至少可能用到多少个 \(4\) 。

例如，当 \(n = 2\) 时，有 \(2 = (4 + 4)/4\)，用到了 \(3\) 个 \(4\)，是最优方案。

试补全程序。

本题类似 dijkstra ，每次选择已经确定最小操作的数字来转移到其他数字。

而 vis 记录已经确定不会再更改操作数的数。

  1. ①处应填（ ）

A. F[4] = 0 B. F[1] = 4 C. F[1] = 2 D. F[4] = 1

首先 \(4\) 需要的操作数是 \(1\) ，\(1\) 需要的是 \(2\) 。

对于程序来说，都是小操作数转移到大操作数。

故选 D 。

  1. ②处应填（ ）

A. !Vis[n] B. r < n

C. F[M] == INT_MAX D. F[n] == INT_MAX

结束掉件首先肯定是 \(n\) 已经算出来了。

但 \(r\) 似乎对本题没有任何影响……

当 \(F_n\) 有值时也不一定是最优的，只有当 \(F_n\) 作为可以去转移别人的时候才是最优的。

故选 A 。

  1. ③处应填（ ）

A. F[i] == r B. !Vis[i] && F[i] == r

C. F[i] < F[x] D. !Vis[i] && F[i] < F[x]

这题真的很像 dij ，选择一个没转移过的但又不会再被转移的数。

选 D 。

  1. ④处应填（ ）

A. F[i] < F[x] B. F[i] <= r C. Vis[i] D. i <= x

两个数转移到新的数，只有当这两个数都是最优的时候，才能保证本次转移不会白转移（指其中一个数再更新本次转移作废）。

故选 C 。

(2)

（RMQ 区间最值问题）给定序列 \(a_1,...,a_n\)，和 \(m\) 次询问，每次询问给定 \(l,r\)，求 \(\max\{ a_1,...,a_n \}\) 。

为了解决该问题，有一个算法叫 the Method of Four Russians ，其时间复杂度为 \(\mathcal{O}(n+m)\) ，步骤如下：

  • 建立 Cartesian（笛卡尔）树，将问题转化为树上的 LCA（最近公共祖先）问题。

  • 对于 LCA 问题，可以考虑其 Euler 序（即按照 DFS 过程，经过所有点，环游回根的序列），即求 Euler 序列上两点间一个新的 RMQ 问题。

  • 注意新的问题为 \(\pm 1\) RMQ，即相邻两点的深度差一定为 \(1\) 。

下面解决这个 \(\pm 1\) RMQ 问题，“序列”指 Euler 序列：

  • 设 \(t\) 为 Euler 序列长度。取 \(b=\left\lceil\dfrac{\log_2 t}{2}\right\rceil\)。将序列每 \(b\) 个分为一大块， 使用 ST 表（倍增表）处理大块间的 RMQ 问题，复杂度 \(\mathcal{O}(\frac{t}{b}\log t)=\mathcal{O}(m)\) 。

  • （重点）对于一个块内的 RMQ 问题，也需要 \(\mathcal{O}(1)\) 的算法。由于差分数组 \(2^{b-1}\) 种，可以预处理出所有情况下的最值位置，预处理复杂度 \(\mathcal{O}(b 2^b)\) ，不超过$ \mathcal{O}(n)$ 。

  • 最终，对于一个查询，可以转化为中间整的大块的 RMQ 问题，以及两端块内的 RMQ 问题。

试补全程序。

我大受震撼。

先把程序大概扫一遍，懂在干嘛。话说为什么我考试的时候都没看到差分这句话？

38.①处应填（ ）

A. p->son[0] = S[top--] B. p->son[1] = S[top--]

C. S[top--]->son[0] = p D. S[top--]->son[1] = p

39.②处应填（ ）

A. p->son[0] = S[top] B. p->son[1] = S[top]

C. S[top]->son[0] = p D. S[top]->son[1] = p

这部分是在建笛卡尔树，笛卡尔树就是对于序列区间 \((l,r)\) ，选取最大值 \(x\) 做为这区间的根，然后再跑 \((l,x-1)\) 和 \((x+1,r)\) ，再和这两个区间的根连边。

可以用单调栈来解决。对于栈顶小于当前元素的情况，显然可以不断弹出，使当前元素找到他最大的左二子。

故 38 题选 A 。

而上述操作结束后，栈顶的元素就比当前元素大，所以可以先把栈顶的右儿子设为当前元素。若后面出现更大的也会覆盖掉。

故 39 题选 D 。

40.③处应填（ ）

A. x->dep < y->dep B. x < y

C. x->dep > y->dep D. x->val < y->val

其实在建完笛卡尔树后，val 就没有用处了。

这部分的 min 是在处理 st 的时候用的，所以是考虑深度。

另外都 min 了不可能去操作 max 的方法吧（（

故选 A 。

41.④处应填（ ）

A. A[i * b + j - 1] == A[i * b + j]->son[0]

B. A[i * b + j]->val < A[i * b + j - 1]->val

C. A[i * b + j] == A[i * b + j - 1]->son[1]

D. A[i * b + j]->dep < A[i * b + j - 1]->dep

首先前面都说了 val 已经没有用了（

因为只有 \(+1\) 和 \(-1\) 两种情况，所以按照题目说法，这里的二进制也是表示这个，用来存储本块内的情况。

故选 D 。

42.⑤处应填（ ）

A. v += (S >> i & 1) ? -1 : 1

B. v += (S >> i & 1) ? 1 : -1

C. v += (S >> (i - 1) & 1) ? 1 : -1

D. v += (S >> (i - 1) & 1) ? -1 : 1

这里是预处理出块内所有的 \(2^{b-1}\) 种情况，方便到时候 \(\mathcal{O}(1)\) 算。

因为刚刚是后者小于前者时为 1 。所以为 1 的时候应该 \(-1\) ，反之 \(+1\) 。

另外注意一下 \(i\) 是从 1 开始的。

故选 D 。

43.⑥处应填（ ）

A. (Dif[p] >> (r - p * b)) & ((1 << (r - l)) - 1)

B. Dif[p]

C. (Dif[p] >> (l - p * b)) & ((1 << (r - l)) - 1)

D. (Dif[p] >> ((p + 1) * b - r)) & ((1 << (r - l + 1)) - 1)

对于一个块内的查询 \((l,r)\) 。

这里的 S 是要确认本区间的状态。

而刚刚的 Dif 已经预处理好了，p 是块的位置。

所以选 C 。

\[\text{by Rainy7} \]

posted @ 2021-09-19 17:15  Rainy7  阅读(8580)  评论(1)  编辑  收藏  举报