「CSP-S 2019」初赛解析

• 前言

  大菜鸡 Rainy7 的总结。

  于 2020/09/25 完成。

---

• 选择题

1.若有定义：int a=7； float x=2.5，y=4.7；则表达式x+a%3*(int)(x+y)%2的值是:(    )

A.0.000000          B.2.750000

C.2.500000          D.3.500000

$$\text{原式} =2.5+(7 \mod 1)(int)(2.5+4.7) \mod 2$$

$$=2.5+7 \mod 2$$

$$=3.5$$

故选 D 。

2.下列属于图像文件格式的有（   ）

A.WMV          B.MPEG

C.JPEG         D.AVI

除了 C 其他都是视频。

补充一下：除了 JPEG 图片后缀还有 JPG、GIF、BMP。

故选 C 。

3.二进制数11 1011 1001 0111 和 01 0110 1110 1011 进行逻辑或运算的结果是（   ）。

A.11 1111 1111 1101

B.11 1111 1111 1101

C.10 1111 1111 1111

D.11 1111 1111 1111

或：有一个是 $1$ 就是 $1$ ，否则为 $0$ 。

$1|1=1,1|0=1,0|1=1,0|0=0$

故选 D 。

4.编译器的功能是（  ）

A.将源程序重新组合

B.将一种语言(通常是高级语言)翻译成另一种语言(通常是低级语言)

C.将低级语言翻译成高级语言

D.将一种编程语言翻译成自然语言

B 是百科原话。一字未改（……）。

故选 B 。

5.设变量x为float型且已赋值，则以下语句中能将x中的数值保留到小数点后两位，并将第三位四舍五入的是（   ）

A.x=(x*100+0.5)/100.0;

B.x=(int)(x*100+0.5)/100.0;

C.x=(x/100+0.5)*100.0;

D.x=x*100+0.5/100.0;

例如一个数 $\overline{ab.cdef}$ 。

$\overline{ab.cdef} \times 100=\overline{abcd.ef}$

进位操作 +0.5 ，可以四舍五入。

然后去掉后面没用的小数 $(int)\overline{abcd.ef}=\overline{abcd}$

还原 $\overline{abcd} / 100 =\overline{ab.cd}$

故选 B 。

6.由数字1，1，2，4，8，8所组成的不同的4位数的个数是（   ）

A.104        B.102

C.98         D.100

$A_4^4=24$

$24+24/2*3+24/2/2=102$

故选 B 。

7.排序的算法很多，若按排序的稳定性和不稳定性分类，则(    )是不稳定排序。

A.冒泡排序

B.直接插入排序

C.快速排序

D.归并排序

算是概念知识了（……），另补充一些其它的知识。

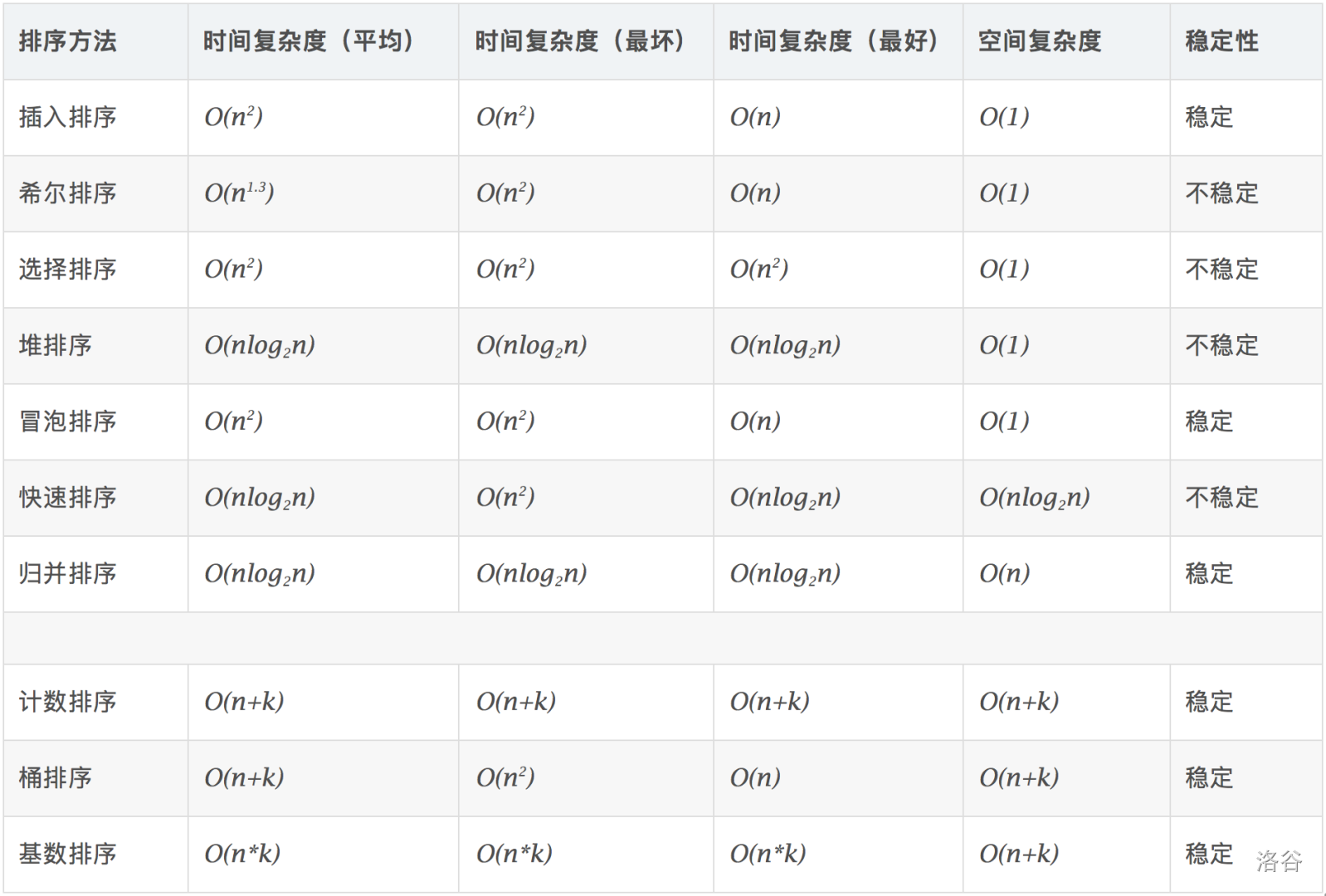
故选 C 。

8.G是一个非连通无向图(没有重边和自环)，共有28条边，则该图至少有(   )个顶点。

A.10          B.9

C.11          D.8

因为至少和非连通无向图。所以很明显可以想到，孤立一个点，然后剩余的点组成一个完全图。

设有 $n$ 个点。

$$\frac{1}{2}(n-1)(n-2)=28$$

$$n=9$$

故选 B 。

9.一些数字可以颠倒过来看，例如0、1、8颠倒过来看还是本身，6颠倒过来是9，9颠倒过来看还是6，其他数字颠倒过来都不构成数字。类似的，一些多位数也可以颠倒过来看，比如106颠倒过来是901。假设某个城市的车牌只有5位数字，每一位都可以取0到9。请问这个城市有多少个车牌倒过来恰好还是原来的车牌，并且车牌上的5位数能被3整除？(     )

A.40          B.25

C.30          D.20

好就是这道题我去年原地白给。

首先是一个五位数，第一位可以确定第五位，第二位可以确认第四位。

所以先不看四，五位。一二位置可以放 $0,1,8,6,9$ 而中间只能放 $0,1,8$ 。

注意到 $2\times 1\equiv2\pmod{3}$ 与 $2\times 8\equiv1\pmod{3}$ 。

所以前两位确定可以确定第三位。

$5 \times 5=25$

故选 B 。

10.一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人？(   )

A.23          B.21

C.20          D.22

容斥， $15+12-4=23$

故选 A 。

11.设A和B是两个长为n的有序数组，现在需要将A和B合并成一个排好序的数组，请问任何以元素比较作为基本运算的归并算法，在最坏情况下至少要做多少次比较？( )

A.$n^2$          B.$n log n$

C.$2n$         D.$2n-1$

考虑最坏情况，为了比较次数最多，所以两个序列轮流取数。

注意到，最后一个数没有的可比。

故选 D 。

12.以下哪个结构可以用来存储图？（   ）

A.栈          B.二叉树

C.队列      D.邻接矩阵

（……）

故选 D 。

13.以下哪些算法不属于贪心算法（   ）。

A.Di.jkstra算法

B.Floyd算法

C.Prim算法

D.Kruskal算法

Floyd 是 DP 思想。

故选 B 。

14.有一个等比数列，共有奇数项，其中第一项和最后一项分别是2和118098，中间一项是486，请问一下哪个数是可能的公比？（         ）。

A.5          B.3

C.4          D.2

$$2x^n=118098$$

$$x^n=59049$$

易得，是 $3$ 的倍数。

故选 B 。

15.有正实数构成的数字三角形排列形式如图所示。第一行的数为 $a(1,1)$ ，第二行 $a(2,1)$ ，$a(2,2)$ ，第 $n$ 行的数为 $a(n,1)$ ，$a(n,2)$ ，…，$a(n,n)$ 。从 $a(1,1)$ 开始，每一行的数 $a(i,j)$ 只有两条边可以分别通向下一行的两个数 $a(i+1,j)$ 和$a(i+1,j+1)$。用动态规划算法找出一条从 $a(1,1)$ 向下通道 $a(n,1)$，$a(n,2)$，…，$a(n,n)$ 中某个数的路径，使得该路径上的数之和最大。

令 $C_{i,j}$ 是从 $a(1,1)$ 到 $a(i,j)$ 的路径上的数的最大和，并且 $C_{i,0}= C_{0,j}=0$ ，则$C_{i,j}$ =( )

A.$\max(C_{i-1,j-1},C_{i-1,j})+ a(i,j)$

B.$C_{i-1,j-1}+C_{i-1,j}$

C.$\max(C_{i-1,j-1},C_{i-1,j})+1$

D.$\max(C_{i,j-1},C_{i-1,j})+ a(i,j)$

（……）数字三角形。

故选 A 。

---

• 阅读程序

我觉得要采取居中码风。

#include <cstdio>
using namespace std;
int n;
int a[100];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    int ans = 1;
    for (int i = 1; i <= n; ++i) {
        if (i > 1 && a[i] < a[i - 1])
            ans = i;
        while (ans < n && a[i] >= a[ans + 1])
            ++ans;
        printf("%d\n", ans);
    }
    return 0;
}

1.第16行输出ans时，ans的值一定大于i。（ ）

考虑反例，当 $ans=i=n$ 时，while 不会跑，所以此时 $ans=i$ 。

故判错 。

2.程序输出的ans小于等于n。（ ）

显然。因为在for中， ans 最多赋值到 n ,while 中也是。

故判对。

3.若将第12行的 < 改为 !=，程序输出的结果不会改变。（ ）

4.当程序执行到第16行时，若 $ans - i> 2$ ,则$a_{i+1} < a_i$。 （ ）

先大致跑一遍，大概知道是这个东西：

$| >x_i | x_i | \le x_i | \le x_i | \le x_i |$

所以第四题成立。判对。

第三题，如果不看 $<$ 就有 $>$ 和 $=$ 。但根据题意只要考虑前者。

$| <x_i | x_i | \le x_i | \le x_i | \le x_i |$

考虑的就是 ans 结果是否改变。

不影响。

故判对。

5.若输入的a数组是一个严格单调递增的数列, 此程序的时间复杂度（ ）

A. O(logn) B. O($n^2$)

C. O(nlogn) D. O(n)

若是严格单调递增，那if就无法执行，ans也不会重置。

故选 D 。

6.最坏情况下，此程序的时间复杂度是( )。

A. O($n^2$)
B. O(logn)
C. O(n)
D. O(nlogn)

严格单调递减，每次 if 都要重置 ans 。每次都要跑一边 while 。

故复杂度为 $n^2$ ，选 A。

#include <iostream>
using namespace std;

const int maxn = 1000;
int n;
int fa[maxn], cnt[maxn];

int getRoot(int v) {
    if (fa[v] == v) return v;
    return getRoot(fa[v]);
}

int main() {
    cin >> n;
    for (int i = 0; i < n; ++i) {
        fa[i] = i;
        cnt[i] = 1;
    }
    int ans = 0;
    for (int i = 0; i < n - 1; ++i) {
        int a, b, x, y;
        cin >> a >> b;
        x = getRoot(a);
        y = getRoot(b);
        ans += cnt[x] * cnt[y];
        fa[x] = y;
        cnt[y] += cnt[x];
    }
    cout << ans << endl;
    return 0;
}

首先，很显然的看出来是并查集。

所以 $fa[]$ 指的是所在集合，$cnt[]$ 指的是集合大小。

1.输入的a和b值应在[0, n-1]的范围内。()

集合的编号范围就是 $[0,n)$ ，不在这个范围肯定不行对吧（

故判对。

2.第16行改成fa[i] = 0；，不影响程序运行结果。( )

如果都设为 $0$ ，那就都在一个集合里了。判错。

3.若输入的 $a$ 和 $b$ 值均在 $[0, n-1]$ 的范围内，则对于任意 $0 \le i<n$ 都有 $0 \le fa[i] <n$ ( )

无论指向那个集合，也只是赋值来赋值去，而初始值就在 $[0,n-1]$ 中，所以判对。

4.若输入的 $a$ 和 $b$ 值均在 $[0, n-1]$ 的范围内，则对于任意 $0 \le i<n$ 都有 $1 \le cnt[i] \le n$ ( )

按道理说集合大小不可能超过 $n$ 的。

但是如果 $a$ 和 $b$ 所在的集合是同一个，那就是同一个集合合并两次 （我 并 我 自 己） 。

所以有可能会大于 $n$ 。

故判错。

5.当 $n$ 等于 $50$ 时，若 $a,b$ 的值都在 $[0,49]$ 的范围内，且在第 $25$ 行时 $x$ 总是不等于 $y$ ,那么输出为()。

A. 1276 B. 1176 C. 1225 D. 1250

你看这个选择题说明怎么合并结果都是一样的。

所以不妨假设，一个一个合并。

$$ans=\sum_{i=1}^{n-1}i \times 1$$

$$ans=\frac{1}{2} \times 50 \times 49$$

$$ans=1225$$

故选 C 。

6.此程序的时间复杂度是()。

A. $O(n)$ B. $O(logn)$ C. $O(n^2)$ D. $O(nlogn)$

注意到，并查集没有压缩路径。

故选 C 。

$t$ 是 $s$ 的子序列的意思是：从 $s$ 中删去若干个字符，可以得到 $t$；特别的，如果 $s=t$ ,那么 $t$ 也是 $s$ 的子序列；空串是任何串的子序列。

例如: $\texttt{acd}$ 是 $\texttt{abcde}$ 的子序列， $\texttt{acd}$ 是 $\texttt{acd}$ 的子序列，但 $\texttt{acd}$ 不是 $\texttt{abcde}$ 的子序列。

$s[x..y]$ 表示 $s[x] ...s[y]$ 共 $y-x+l$ 个字符构成的字符串，若 $x>y$ 则 $s[x..y]$ 是空串。$t[x..y]$ 同理。

#include <iostream>
#include <string>
using namespace std;
const int max1 = 202;
string s, t;
int pre[max1], suf[max1];

int main() {
    cin >> s >> t;
    int slen = s.length(), tlen = t.length();

    for (int i = 0, j = 0; i < slen; ++i) {
        if (j < tlen && s[i] == t[j]) ++j;
        pre[i] = j; // t[0..j-1] 是 s[0..i] 的子序列
    }

    for (int  i = slen - 1 , j = tlen - 1; i >= 0; --i) {
        if(j >= 0 && s[i] == t [j]) --j;
        suf[i]= j; // t[j+1..tlen-1] 是 s[i..slen-1] 的子序列
    }

    suf[slen] = tlen -1;
    int ans = 0;
    for (int i = 0, j = 0, tmp = 0; i <= slen; ++i){
        while(j <= slen && tmp >= suf[j] + 1) ++j;
        ans = max(ans, j - i - 1);
        tmp = pre[i];
    }
    cout << ans << endl;
    return 0;
}
/*
提示： t[0..pre[i] -1]是 s[0..i]的子序列；
t[suf[i]+1..tlen-1]是 s[i..slen-1]的子序列。
*/

本题是求 $s$ 中连续删除至多几个字母后，$t$ 仍然是 $s$ 的子序列。

但是其实这点不好看。但是做题的时候能大致猜出一个方向（

1.程序输出时，$suf$ 数组满足：对任意 $0 \le i < slen$ , $suf[i] \le suf[i + 1]$ 。 （）

在循环中，可以看出随着 $i$ 的减少， $j$ 从未递增。

故判对。

2.当 $t$ 是 $s$ 的子序列时，输出一定不为 $0$ 。（）

考虑举反例。

当两个都为空串的时候，答案就是 $0$ 。

但是不能有空串（要输入）；所以退一步。

假设 $t=s=\texttt{a}$ ，结果为 $0$ 。

故判错。

3.程序运行到第 $23$ 行时，j-i-1 一定不小于 $0$ 。（）

还是考虑举反例。

想到为了让其危负数，那 while 就不执行。

设 $s=\texttt{a}, t=\texttt{b}$ ，所以 $j-i-1=0-0-1=-1<0$ 。

故判错。

4.当 $t$ 是 $s$ 的子序列时，$pre$ 数组和 $suf$ 数组满足：对任意 $0 \le i < slen, pre[i] > suf[i + 1] + 1$ 。 （）

因为 $t[0..pre[i]-1],t[sub[i+1]+1..lent-1]$ 是 $s[0..i],s[i+1..lens-1]$ 的子序列。

所以不会重叠。

$$pre[i]-1 < suf[i+1]+1$$

$$pre[i] \le suf[i+1]+1$$

故判错。

5.若 $tlen=10$ ,输出为 $0$ ,则 $slen$ 最小为（）

A. 10 B. 12 C. 0 D. 1

首先，当 $s$ 为空串的时候，输出也是为 $0$ 。

但是不能为空串，所以退一步，当 $s$ 长度为 $1$ 。

故选 D 。

6.若 $tlen=10$ ,输出为 $2$ ,则 $slen$ 最小为（）。

A. 0 B. 10 C. 12 D. 1

$t$ 有10个字母，$s$ 为 含子序列 $t$ 的一串东西 和删除的 $2$ 个字母。

考虑最小，那串东西就是 $t$ ，所以 $10+2=12$ 。

故选 C 。

---

• 完善程序

（匠人的自我修养）一个匠人决定要学习 $n$ 个新技术。要想成功学习一个新技术，他不仅要拥有一定的经验值，而且还必须要先学会若干个相关的技术。学会一个新技术之后，他的经验值会增加一个对应的值。给定每个技术的学习条件和习得后获得的经验值，给定他已有的经验值，请问他最 多能学会多少个新技术。
输入第一行有两个数，分别为新技术个数 $n(1 \le n \le 10^3)$ ,以及己有经验值$(\le 10^7)$

接下来n行。第i行的两个正整数，分别表示学习第i个技术所需的最低经验值 $(\le 10^7)$,以及学会第i个技术后可获得的经验值 $(\le 10^7)$ 。

接下来 $n$ 行。第 $i$ 行的第一个数 $m_i(1 \le m_i < n)$ ,表示第 $i$ 个技术的相关技术数量。紧跟着 $m$ 个两两不同的数，表示第 $i$ 个技术的相关技术编号。

输出最多能学会的新技术个数。

下面的程序以 $(n^2)$ 的时间复杂度完成这个问题，试补全程序。

#include<cstdio>
using namespace std;
const int maxn = 1001;

int n;
int cnt[maxn];
int child [maxn][maxn];
int unlock[maxn];
int threshold[maxn], bonus[maxn];
int points;
bool find(){
    int target = -1;
    for (int i = 1; i <= n; ++i)
        if(① && ②){
            target = i;
            break;
    }
    if(target == -1)
        return false;
    unlock[target] = -1;
    ③
    for (int i = 0; i < cnt[target]; ++i)
        ④
    return true;
}

int main(){
    scanf("%d%d", &n, &points);
    for (int i = 1; i <= n; ++i){
        cnt[i] = 0;
        scanf("%d%d", &threshold[i], &bonus[i]);
    }
    for (int i = 1; i <= n; ++i){
        int m;
        scanf("%d", &m);
        ⑤
        for (int j = 0; j < m; ++j){
            int fa;
            scanf("%d", &fa);
            child[fa][cnt[fa]] = i;
            ++cnt[fa];
        }
    }

    int ans = 0;
    while(find())
        ++ans;

    printf("%d\n", ans);
    return 0;
}

①处应填（）

A. unlock[i] <= 0

B. unlock[i] >= 0

C. unlock[i] == 0

D. unlock[i] == -1

②处应填（）

A. threshold[i] > points

B. threshold[i] >= points

C. points > threshold[i]

D. points >= threshold[i]

③处应填（）

A. target = -1

B. --cnt[target]

C. bonus[target] = 0

D. points += bonus[target]

④处应填（）

A. cnt[child[target][i]] -= 1

B. cnt[child[target][i]] = 0

C. unlock[child[target][i]] -= 1

D. unlock[child[target][i]] = 0

⑤处应填（）

A. unlock[i] = cnt[i]

B. unlock[i] = m

C. unlock[i] = 0

D. unlock[i] = -1

大致看完程序，发现其实是一个拓扑排序。每次 $find()$ 找的是可以选择的课程。

根据第②题，可以推出， $points$ 是总经验值。

而 $unlock[]$ ，根据⑤，因为如果为 $0$ 等于没有这行。再看①，可以推测出 $unlock_i$ 表示第 $i$ 个学科还差几个学科。

所以⑤选 B ，①选 C 。

看③，首先排除 A 和 B 。而删除 $bonus$ 的没有用，$points$ 反而要加上所得经验值。故选 D 。

看④，推测要改变 $unlock$ 要学的科目数减一，故选 C 。

(取石子)Alice和Bob两个人在玩取石子游戏。他们制定了 $n$ 条取石子的规则，第 $i$ 条规则为：如果剩余石子的个数大于等于 $a[i]$ 且大于等于 $b[il$ ，那么他们可以取走 $b[i]$ 个石子。

他们轮流取石子。如果轮到某个人取石子， 而他无法按照任何规则取走石子，那么他就输了。一开始石子有 $m$ 个。请问先取石子的人是否有必胜的方法？

输入第一行有两个正整数，分别为规则个数 $n (1<n<64)$ ,以及石子个数 $m (<=10^7)$ 。

接下来 $n$ 行。第 $i$ 行有两个正整数 $a[i]$ 和 $b[i]$ 。$(1 \le a[i] \le 10^7,1 \le b[i] \le 64)$ 。

如果先取石子的人必胜，那么输出Win，否则输出Loss。

提示：

可以使用动态规划解决这个问题。由于 $b[i]$ 不超过 $64$ ,所以可以使用 $64$ 位无符号整数去压缩必要的状态。

$status$ 是胜负状态的二进制压缩，$trans$ 是状态转移的二进制压缩。

#include <cstdio>
#include<algorithm>
using namespace std;
const int maxn = 64;
int n, m;
int a[maxn], b[maxn];
unsigned long long status, trans;
bool win;
int main(){
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i)
        scanf("%d%d", &a[i], &b[i]);
    for(int i = 0; i < n; ++i)
        for(int j = i + 1; j < n; ++j)
            if (aa[i] > a[j]){
                swap(a[i], a[j]);
                swap(b[i], b[j]);
            }
    status = ①;
    trans = 0;
    for(int i = 1, j = 0; i <= m; ++i){
        while (j < n && ②){
            ③;
            ++j;
        }
        win = ④;
        ⑤;
    }

    puts(win ? "Win" : "Loss");

    return 0;
}	

①处应填( )

A. 0 B. ~0ull C. ~0ull^1 D. 1

因为是 DP ，所以可以看出来 DP 的有一维被压掉了。

我感觉， 其实 $status$ 本来是一维数组。

所以初始状态时，石头数量为 $0$ 。

所以无论如何先手必胜。

故选 C 。

②处应填( )

A. a[j] < i B. a[j] == i C. a[j] !=i D. a[j]>1

while 中要判断的是能满足条件的。

其实应是 $a_j \le i$ ，但开头有排序过，所以等价于 $a_j=i$ 。

故选 B 。

③处应填( )

A. trans |=1ull << (b[j] - 1)

B. status |=1ull << (b[j] - 1)

C. status +=1ull << (b[j] - 1)

D. trans +=1ull << (b[j] - 1)

首先，位运算咋有 + 呢？所以排除 C 和 D 。

有已知得， $trans$ 是 DP 转移中的变量，而这个空显然在转移中（，所以排除 B 。

故选 A 。

④处应填( )

A. ~status| trans B. status & trans

C. status | trans D. ~status & trans

转移完了。

所以是当前状态（转移状态 $trans$ ）和上次状态 $status$ 合并。

所以如果上次先手输了，这次就可以先取这次的石头。上次取完了这波石头是后手先取。

所以 $status$ 状态取反。

所以是与操作，选 D 。

⑤处应填( )

A. trans =status | trans ^ win

B. status = trans >> 1 ^ win

C. trans =status ^ trans | win

D. status = status << 1 ^ win

首先肯定是 $status$ 转移，排除 A 和 C 。

要转入下一个更多石子的局面，肯定是从当前局面输赢起步，所以不可能是 B 。

选 D 。

---

$$\text{by Rainy7}$$