「舞蹈链 DLX 」学习笔记
-
前言
挖坑,开始填。--2021/04/26
填完了(?竟然没鸽。) --2021/04/27
《关于我不想搞 whk 于是就来写博客这件事。》
不是什么鬼啊喂。
如果有不足的地方欢迎随时指出,然后求赞(?)。
-
DLX 是什么
Dancing Links X 即舞蹈链是一种高效的数据结构,用来优化一些搜索。
处理的问题主要包括 \(2\) 种类型,一类是精确覆盖问题,另一类是重复覆盖问题。
那么接下来先给出精确覆盖问题的模板题,即洛谷 P4929 【模板】舞蹈链(DLX)。
给定一个 \(n\) 行 \(m\) 列的矩阵,矩阵中每个元素要么是 \(1\) ,要么是 \(0\) 。
你需要在矩阵中挑选出若干行,使得对于矩阵的每一列 \(j\) ,在你挑选的这些行中,有且仅有一行的第 \(j\) 个元素为 \(1\) 。
首先易得,大暴搜的复杂度是 \(\mathcal{O}(m\cdot2^n)\)
实际上,这属于 NP 完全问题,也就是没有多项式算法。
但是 DLX 却可以在大大提高搜索的效率,在本题中,可以解决的范围为 \(n,m \le 500\) ,其中保证矩阵中 \(1\) 的数量不超过 \(5000\) 个。
重复覆盖问题类似,只有两点不同。下边已加粗。
由于洛谷并没有重复覆盖模板题,所以以下给出模板问题:
给定一个 \(N\) 行 \(M\) 列的矩阵,矩阵中每个元素要么是 \(1\) ,要么是 \(0\) 。
你需要在矩阵中选择若干行,使每一列都至少包含一个 \(1\) ,并且要求选择的行数最少。
-
十字链表
专门用来 DLX 的东西,属于前置知识。
顾名思义,十字样子的链表。下面用 \(row_i\) 表示行 \(col_j\) 表示列。以下是十字链表初始状态
,什么中间太空了放点东西好耶。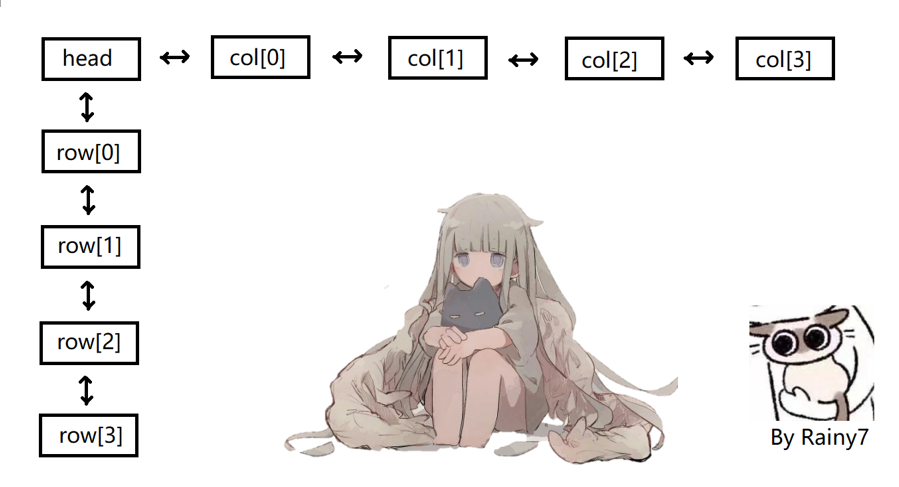
接下来,因为我不喜欢这个样例,所以我手造一个来讲吧。
1 0 0 0 1 0 1 0 1首先加上第一个点 \((1,1)\) 。

同理,加上点 \((2,2)\) 和 \((3,3)\) 。
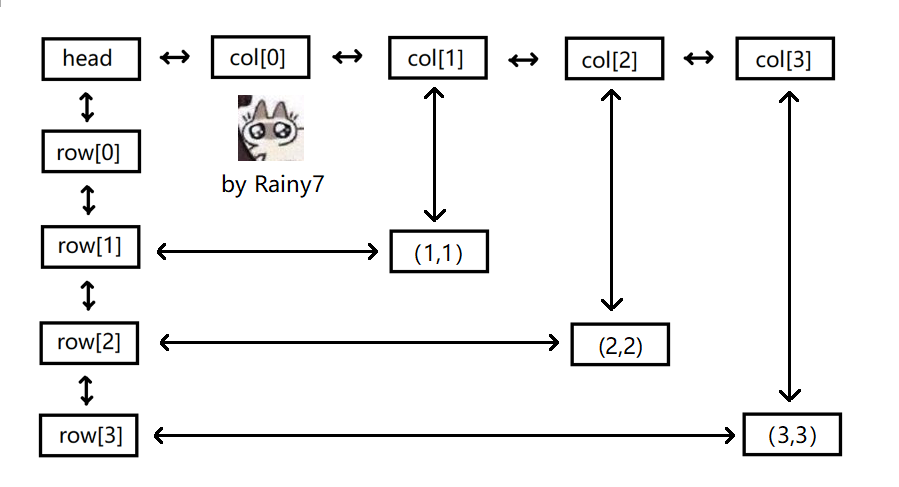
然后加上 \((3,1)\) 。
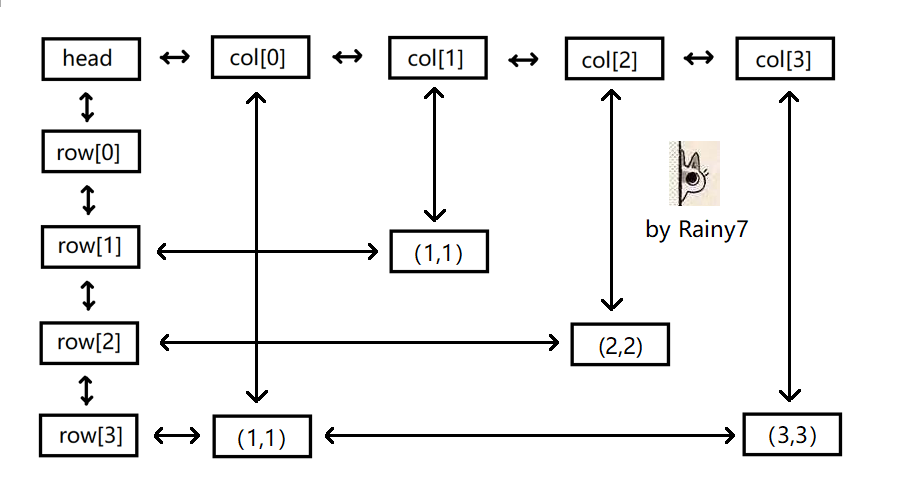
删除的时候,类似把上面的图倒着看(?)。
这些就是十字链表的要用的知识了。下面进入正题。
-
精确覆盖问题
首先,先来考虑大暴搜如何优化。
给定一个矩阵。
1 1 1 0 0 0 0 0 0 1 1 1 0 1 0 0 0 1 1 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0比如我们首先选了第 \(1\) 行,然后发现第一行的前 \(3\) 列都是 \(1\) 。
那么我们肯定不能再选含有前 \(3\) 列为 \(1\) 的行,也就是第 \(2,4\) 行。
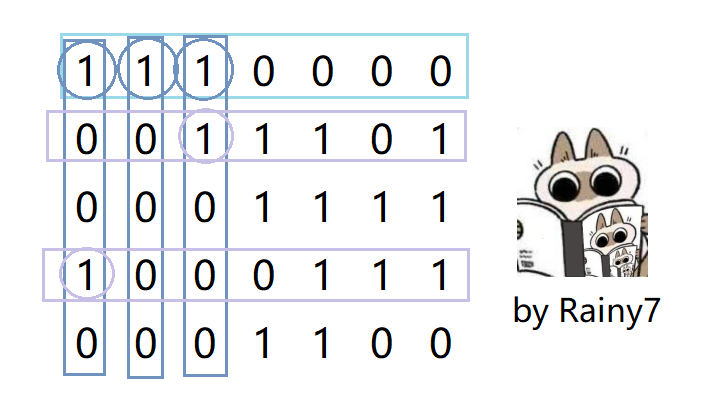
那么我们将他们一起删除。
那么接下来也就同理了。
当所有列都被删后,就可以判定有解并且返回了。
所以接下来的问题就是如何高效判断要删除的行。
很自然的想到了十字链表
(因为他是前置知识),每次删除时,在对应一列下去的把每个点对应一横溜过去的每个点都删掉。所以可以发现,DLX 的效率和 \(1\) 数量有关。
此外,每次找行是,我们优先选择一行里面 \(1\) 数量最多的列。
另外,因为是在 dfs 中,所以回溯的时候要把删的点在加回去。
现在放出代码。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int Maxn=5000+500+10;
int n,m,l[Maxn],r[Maxn],u[Maxn],d[Maxn];// 十字链表左右上下
int idx,ansn,ans[Maxn],s[Maxn],row[Maxn],col[Maxn];
void init() // 预处理
{
for(int i=0;i<=m;i++)
{
l[i]=i-1;r[i]=i+1;
u[i]=d[i]=i;
}
l[0]=m;r[m]=0; // 注意十字链表是收尾相接
idx=m+1;
}
void add(int &hd,int &tl,int x,int y) // 十字链表加点
{
row[idx]=x;col[idx]=y;s[y]++;
u[idx]=y;d[idx]=d[y];u[d[y]]=idx;d[y]=idx;
r[hd]=l[tl]=idx;r[idx]=tl;l[idx]=hd;
tl=idx++;
}
void remove(int p) // 删除
{
r[l[p]]=r[p];l[r[p]]=l[p];
for(int i=d[p];i!=p;i=d[i])
for(int j=r[i];j!=i;j=r[j])
{
s[col[j]]--;
u[d[j]]=u[j];d[u[j]]=d[j];
}
}
void resum(int p) // 复原
{
for(int i=u[p];i!=p;i=u[i])
for(int j=l[i];j!=i;j=l[j])
{
u[d[j]]=j;d[u[j]]=j;
s[col[j]]++;
}
r[l[p]]=p;l[r[p]]=p;
}
bool dfs()
{
if(!r[0])return 1;
int p=r[0];
for(int i=r[0];i;i=r[i])
if(s[i]<s[p])p=i; // 优先选择一行里面 1 多的列。
remove(p);
for(int i=d[p];i!=p;i=d[i])
{
ans[++ansn]=row[i];
for(int j=r[i];j!=i;j=r[j])remove(col[j]);
if(dfs())return 1;
for(int j=l[i];j!=i;j=l[j])resum(col[j]);
ansn--;
}
resum(p);
return 0;
}
int main()
{
scanf("%d%d",&n,&m);
init();
for(int i=1;i<=n;i++)
{
int hd=idx,tl=idx;
for(int j=1;j<=m;j++)
{
int x;
scanf("%d",&x);
if(x)add(hd,tl,i,j);
}
}
if(dfs())
for(int i=1;i<=ansn;i++)
printf("%d ",ans[i]);
else printf("No Solution!");
printf("\n");
return 0;
}
-
重复覆盖问题
解决方法和精确覆盖类似,但有前置知识 IDA* 算法。 建议没有学过的先去补一下。
因为是至少一个 \(1\) ,所以同一列存在多个 \(1\) 是合法的。
换句话说,就相当于我们之前的同时删除多个行的做法,不 行 了 。
那么就相当于之前找列也没意义了,因为每一列都有可能。
所以我们简单改一下代码。
首先是修改和恢复部分,不再需要删除一列过去的点。
每次优先找到 \(1\) 最多的列时,也不再需要删除这一列了。
但是这样效率明显差很多了。
于是我们考虑类似 IDA* 来搞。
先用一个数组 \(tot\) 来从小到大枚举要的行数,在 dfs 中用一个估价函数,估一下目前还要多少行,如果当前行数加上估价函数大于 \(tot\) 返回无解即可。
而估价函数呢,用贪心技数下就可以了。
具体详见代码。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int Maxn=10000+5;
int n,m,l[Maxn],r[Maxn],u[Maxn],d[Maxn],s[Maxn];
int idx,tot,ans[Maxn],col[Maxn],row[Maxn];
bool st[Maxn];
void init()
{
for(int i=0;i<=m;i++)
{
l[i]=i-1;r[i]=i+1;
u[i]=d[i]=col[i]=i;
s[i]=0;
}
l[0]=m;r[m]=0;
idx=m+1;
}
int h() //估价函数
{
int cnt=0;
memset(st,0,sizeof(st));
for(int i=r[0];i;i=r[i])
{
if(st[col[i]])continue;
cnt++;
st[col[i]]=1;
for(int j=d[i];j!=i;j=d[j])
for(int k=r[j];k!=j;k=r[k])
st[col[k]]=1;
}
return cnt;
}
void add(int &hd,int &tl,int x,int y)
{
row[idx]=x;col[idx]=y;s[y]++;
u[idx]=y;d[idx]=d[y];u[d[y]]=idx;d[y]=idx;
r[hd]=l[tl]=idx;r[idx]=tl;l[idx]=hd;
tl=idx++;
}
void remove(int p) // 注意列并不会删除
{
for(int i=d[p];i!=p;i=d[i])
r[l[i]]=r[i],l[r[i]]=l[i];
}
void resum(int p) // 同上
{
for(int i=u[p];i!=p;i=u[i])
r[l[i]]=i,l[r[i]]=i;
}
bool dfs(int k)
{
if(k+h()-1>tot)return 0;
if(!r[0])return 1;
int p=r[0];
for(int i=r[0];i;i=r[i])
if(s[p]>s[i])p=i;
// 注意选完列,p 所在的列并不会删除。
for(int i=d[p];i!=p;i=d[i])
{
ans[k]=row[i];
remove(i);
for(int j=r[i];j!=i;j=r[j])remove(j);
if(dfs(k+1))return 1;
for(int j=l[i];j!=i;j=l[j])resum(j);
resum(i);
}
return 0;
}
int main()
{
scanf("%d%d",&n,&m);
init();
for(int i=1;i<=n;i++)
{
int hd=idx,tl=idx;
for(int j=1;j<=m;j++)
{
int x;
scanf("%d",&x);
if(x)add(hd,tl,i,j);
}
}
tot=0;
while(!dfs(1))tot++;
printf("%d\n",tot);
for(int i=1;i<=tot;i++)
printf("%d ",ans[i]);
return 0;
}
-
DLX 的练习题
这是我之前整理的一份题单:「舞蹈链DLX」の 学习题单 。
但是因为我题刷的少,见识也少,题单里的题数不多,还有 \(2,3\) 题几乎是多倍经验。
但题单是处于持续更新状态,如果往后做题还碰到,会不定期的补充,也欢迎大家来补充。
下面举例两个例题。
-
SP1110 SUDOKU - Sudoku
题目链接:Link.
一个数独的网格是由 \(16 \times 16\) 个小格组成的, 这些小格又被分为 \(4 \times 4=16\) 个小组, 一些小格填入了从 \(A\) 至 \(P\) (字母表前 \(16\) 个)的字母,不过一般填成数字。
游戏目的是将所有小格填满,而使每行,每列和每个\(4 \times 4\) 小组中不重复的包含这 \(16\) 个字母。
给出的初始状态满足以上要求且满足唯一解。
说真的,做舞蹈链的题,你首先不能把他当矩阵看(数独是真的算很经典的题了。
首先我们简化一下题目,对于一个 \(16 \times 16\) 的矩阵,每一行必须有 \(1-16\) ,每一列必须有 \(1-16\) ,每一 \(16\) 宫格必须有 \(1-16\) 。
再换个说法,比如我们定义一个 \((i,j,k) \in \{ 0,1 \}\) ,表示位于 \((i,j)\) 填的数字是否 \(k\) 。
也就是,对于一个 \(16 \times 16\) 的矩阵,每一行都必须满足对于每个 \(k\) ,存在一个为 \(1\) , 每一列都必须满足对于每个 \(k\) ,存在一个为 \(1\) ,每一宫格都必须满足对于每个 \(k\) ,存在一个为 \(1\) 。
发现这就是个 DLX 精确覆盖问题。
那么问题解决了。具体代码细节如下:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int Maxn=20000;
struct node{
int x,y;
char c;
}op[Maxn];
int m=16*16*4,l[Maxn],r[Maxn],u[Maxn],d[Maxn];// 十字链表左右上下
int idx,ansn,ans[Maxn],s[Maxn],row[Maxn],col[Maxn];
char c[20][20];
void init() // 预处理
{
for(int i=0;i<=m;i++)
{
l[i]=i-1;r[i]=i+1;s[i]=0;
u[i]=d[i]=i;
}
l[0]=m;r[m]=0;
idx=m+1;
}
void add(int &hd,int &tl,int x,int y)
{
row[idx]=x;col[idx]=y;s[y]++;
u[idx]=y;d[idx]=d[y];u[d[y]]=idx;d[y]=idx;
r[hd]=l[tl]=idx;r[idx]=tl;l[idx]=hd;
tl=idx++;
}
void remove(int p)
{
r[l[p]]=r[p];l[r[p]]=l[p];
for(int i=d[p];i!=p;i=d[i])
for(int j=r[i];j!=i;j=r[j])
{
s[col[j]]--;
u[d[j]]=u[j];d[u[j]]=d[j];
}
}
void resum(int p)
{
for(int i=u[p];i!=p;i=u[i])
for(int j=l[i];j!=i;j=l[j])
{
u[d[j]]=j;d[u[j]]=j;
s[col[j]]++;
}
r[l[p]]=p;l[r[p]]=p;
}
bool dfs()
{
if(!r[0])return 1;
int p=r[0];
for(int i=r[0];i;i=r[i])
if(s[i]<s[p])p=i;
remove(p);
for(int i=d[p];i!=p;i=d[i])
{
ans[++ansn]=row[i];
for(int j=r[i];j!=i;j=r[j])remove(col[j]);
if(dfs())return 1;
for(int j=l[i];j!=i;j=l[j])resum(col[j]);
ansn--;
}
resum(p);
return 0;
}
void w()
{
memset(r,0,sizeof(r));memset(u,0,sizeof(u));
memset(l,0,sizeof(l));memset(u,0,sizeof(u));
memset(s,0,sizeof(s));
memset(col,0,sizeof(col));
memset(row,0,sizeof(row));
}
int main()
{ int T,cases=0;
scanf("%d",&T);
while(T--)
{
for(int i=0;i<16;i++)
scanf("%s",c[i]);
if(cases)printf("\n");
cases++;
w();
init();
for(int i=0,n=1;i<16;i++)
for(int j=0;j<16;j++)
{
int a=0,b=15;
if(c[i][j]!='-')a=b=c[i][j]-'A';
for(int k=a;k<=b;k++,n++)
{
int hd=idx,tl=idx;
op[n].x=i;op[n].y=j;op[n].c=k+'A';
add(hd,tl,n,i*16+j+1);
add(hd,tl,n,256+i*16+k+1);
add(hd,tl,n,256*2+j*16+k+1);
add(hd,tl,n,256*3+(i/4*4+j/4)*16+k+1);
}
}
dfs();
for(int i=1;i<=ansn;i++)
c[op[ans[i]].x][op[ans[i]].y]=op[ans[i]].c;
for(int i=0;i<16;i++)
printf("%s\n",c[i]);
}
return 0;
}
-
UVA1603 破坏正方形 Square Destroyer
这篇我甚至写过题解那就直接复制过来嗯就这样。题目链接:Link.
一个 \(n \times n\) 的网格,共 \(2 \times n \times (n + 1)\) 条边,现在已经删除了一些边,问至少还需删去多少边,以使得剩下的边不能构成正方形。
一个正方形有 \(4\) 条边(每条边若干火柴),选择一根火柴就可以破坏掉正方形。但是也可以选择多根。
要保证每个正方形内部至少有一根火柴被选择,且要求选择火柴数量最少。
再想想重复覆盖问题。
很明显,这是一道重复覆盖问题。
接下来就是如何构建了。
首先,把这些火柴抽象成 \(2n(n+1)\) 个点。
然后每根火柴和所在边长为 \(len (1 \le len \le n)\) 的矩形的边上所有火柴连起来。
如下图:(举例点 \(1\)

具体细节见代码,以下为代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;
const int Maxn=3600+5;
int T,n,m,l[Maxn],r[Maxn],u[Maxn],d[Maxn],s[Maxn];
int idx,tot,ans[Maxn],col[Maxn],row[Maxn];
bool st[Maxn]; // 1.作为估价函数 2.作为建图
vector<int> sq[60];
void init()
{
for(int i=0;i<=m;i++)
{
l[i]=i-1;r[i]=i+1;
u[i]=d[i]=col[i]=i;
s[i]=0;
}
l[0]=m;r[m]=0;
idx=m+1;
}
int h() //估价函数
{
int cnt=0;
memset(st,0,sizeof(st));
for(int i=r[0];i;i=r[i])
{
if(st[col[i]])continue;
cnt++;
st[col[i]]=1;
for(int j=d[i];j!=i;j=d[j])
for(int k=r[j];k!=j;k=r[k])
st[col[k]]=1;
}
return cnt;
}
void add(int &hd,int &tl,int x,int y)
{
row[idx]=x;col[idx]=y;s[y]++;
u[idx]=y;d[idx]=d[y];u[d[y]]=idx;d[y]=idx;
r[hd]=l[tl]=idx;r[idx]=tl;l[idx]=hd;
tl=idx++;
}
void remove(int p)
{
for(int i=d[p];i!=p;i=d[i])
r[l[i]]=r[i],l[r[i]]=l[i];
}
void resum(int p)
{
for(int i=u[p];i!=p;i=u[i])
r[l[i]]=i,l[r[i]]=i;
}
bool dfs(int k)
{
if(k+h()-1>tot)return 0;
if(!r[0])return 1;
int p=r[0];
for(int i=r[0];i;i=r[i])
if(s[p]>s[i])p=i;
for(int i=d[p];i!=p;i=d[i])
{
ans[k]=row[i];
remove(i);
for(int j=r[i];j!=i;j=r[j])remove(j);
if(dfs(k+1))return 1;
for(int j=l[i];j!=i;j=l[j])resum(j);
resum(i);
}
return 0;
}
int main()
{
scanf("%d",&T);
while(T--)
{
int k;
scanf("%d%d",&n,&k);
m=idx=0;
memset(st,0,sizeof(st));
memset(col,0,sizeof(col));
for(int i=1;i<=k;i++)
{
int x;
scanf("%d",&x);
st[x]=1;
}
for(int len=1;len<=n;len++)
for(int x=1;x+len-1<=n;x++)
for(int y=1;y+len-1<=n;y++)
{
m++;
sq[m].clear();
int dd=n*2+1;//一行过去(横n加上竖n+1)个数
for(int i=0;i<len;i++) //向一个矩形的 4 边(上下左右)连去
{
sq[m].push_back((x-1)*dd+y+i); //上
sq[m].push_back((x-1)*dd+y+i+dd*len); //下
sq[m].push_back((x-1)*dd+y+n+i*dd); //左
sq[m].push_back((x-1)*dd+y+n+i*dd+len); //右
}
for(int i=0;i<sq[m].size();i++) //相连的边有一个断了,直接删除所有即可
if(st[sq[m][i]]){m--;break;}
}
init();
for(int i=1;i<=n*(n+1)*2;i++) //全部边
if(!st[i])
{
int hh=idx,tl=idx;
for(int j=1;j<=m;j++)
if(find(sq[j].begin(),sq[j].end(),i)!=sq[j].end()) //连边存在
add(hh,tl,i,j);
}
tot=0;
while(!dfs(1))tot++;
printf("%d\n",tot);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号