「CF1608D」Dominoes - 题解

• 分析

  首先，最后若干个骨牌一定满足有 \(n\) 个黑色，\(n\) 个白色。

  先考虑不存在一个骨牌上两个格子同一个颜色的情况（即保证每个骨牌都是一黑一白）。那么最后的染色结果一定只有 左边都是黑色 或者 右边都是黑色 的 2 种情况。

  如果存在一个骨牌全是黑色，那么也一定存在一个骨牌全是白色。

  我们发现，用这种全黑（或白）骨牌可以将左黑右白的骨牌与左白右黑的骨牌分开，使他们合法。

  

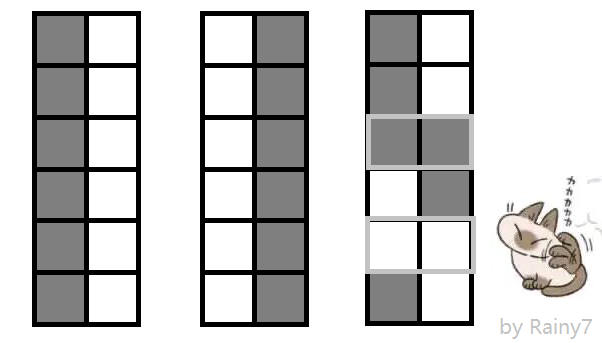
  也就是说，如果骨牌中存在全黑（白）骨牌，那么剩下的颜色在满足 \(n\) 个黑色 \(n\) 个白色的情况下，就可以随意取。

  接下来考虑初始情况。设初始给了 \(s_w\) 个白色和 \(s_b\) 个黑色。

  如果初始情况存在一个全黑（白）骨牌，那么答案即为 \(C_{2n-s_w-s_b}^{n-s_w}\) 。

  如果初始不存在，用上面那个组合数再减去不合法情况即可。

  即减去没有染色出全黑（白）骨牌的所有情况，再加上 左边都是黑色 或者 右边都是黑色 的 2 种情况。注意一下这两种情况是否会出现即可。

---

• 代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int N=2e5+5;
const int Mod=998244353;
int n,ans,cnt,s1,s2,cnt1,cnt2,mul[N],inv[N];
char s[N][5];
int qpow(int x,int k)
{	int res=1;
	while(k)
	{	if(k&1)res=1ll*res*x%Mod;
		x=1ll*x*x%Mod;
		k>>=1;
	}
	return res;
}
int C(int x,int y){
	return 1ll*mul[y]*inv[x]%Mod*inv[y-x]%Mod;
}
int main()
{	scanf("%d",&n);
	mul[0]=inv[0]=1;
	for(int i=1;i<=(N-5);i++)mul[i]=1ll*mul[i-1]*i%Mod,inv[i]=qpow(mul[i],Mod-2);
	for(int i=1;i<=n;i++)
	{	scanf("%s",s[i]);
		cnt+=(s[i][0]!='?')+(s[i][1]!='?');
		s1+=(s[i][0]=='W')+(s[i][1]=='W');
		s2+=(s[i][0]=='B')+(s[i][1]=='B');
	}
//	printf("cnt:%d s1:%d s2:%d\n",cnt,s1,s2);
	for(int i=1;i<=n;i++)
	{	if(s[i][0]=='W'&&s[i][1]=='W')cnt1++;
		if(s[i][0]=='B'&&s[i][1]=='B')cnt2++;
	}
//	printf("C:%d %d\n",n-s1,2*n-cnt);
	if(cnt1||cnt2)printf("%d\n",C(n-s1,2*n-cnt));
	else{
		ans=C(n-s1,2*n-cnt);
		cnt1=cnt2=0;
		for(int i=1;i<=n;i++)
		{	if(s[i][0]=='W'||s[i][1]=='B')cnt1++;
			if(s[i][1]=='W'||s[i][0]=='B')cnt2++;
		}
//		printf("%d\n",ans);
//		printf("%d %d\n",cnt1,cnt2);
		if(!cnt1)ans++;
		if(!cnt2)ans++;
		ans=(1ll*ans+Mod-qpow(2,n-cnt1-cnt2))%Mod;
		printf("%d\n",ans);
	}
	return 0;
}