「2022/09&10」学习记录
质量！！质量！！！虽说不用题解的那种质量，但至少不要敷衍到自己都看不懂啊！！！！
—— 11 月怒吼并尝试立下 flag 的 Rainy7
你看摘要了吗。
9 月没停课。题不多，所和 10 月合并了。（什么什么难道不是因为都 10 月了然后你 9 月的还没写完吗（）
本来 9 月底要停课，停课单都写好了，但是一脱加上国庆放假就变成国庆后停课了（？）。
讨厌在家网课啊。写题效率极低。
要死力。以后不堆着写了，到后面越写越简略还写不下去（捂脸）我看看能不能一周写一次吧。我怎么感觉这后面的学习记录质量还没 04 那个高（？）。
另提，新班级真不错！同桌还是 llx 简直起飞。因为我可能社交比较厉害还是什么的，我直接选择不去破冰班会，因为我觉得我不需要（逃），事实证明确实（笑死我了）。新的老师也挺好的，好耶！！！
顺便，我发现 CSP vp 可能全省垫底了（）我实在不理解我当时为什么要自信跳过 T3 题目都不看那种。然后写 T4。但我码力又不够。（）
来点传统艺能。
从来没有人许诺会给我们天堂
苦尽后甘来，是什么让我如此臆想
若再来一次，我绝不再选择盛放
这样卫道士就不会从正面朝我心，开上一枪——《我对孤独一无所知》
「AGC039D」Incenters
在平面中给定\(n\)个位于单位圆上的点，坐标形如\((\cos\frac{2\pi T_i}{L},\sin\frac{2\pi T_i}{L})\)，等概率随机地选取其中不同的三个点组成三角形，求三角形的内心（即，内切圆的圆心）的横纵坐标期望。
保证 \(3\le n\le 3000, n\le L\le 10^9, 0\le T_i< L, T_i\le T_{i+1}\)。
什么数竞题！！！
首先做三角形 $\vartriangle ABC $ 三条边的中垂线，连接延长交圆三个点 \(D,E,F\)。则 \(\vartriangle ABC\) 的内心是 \(\vartriangle DEF\) 的垂心。
然后根据欧拉线，不妨设 \(\vartriangle ABC\) 的重心垂心为 \(G,H\) 于是有 \(GH = 2 OG\)。
于是对于任意三角形，三段弧中点坐标和就是三角形内心的坐标。
然后就很轻松了。
「AHOI2022」回忆
有一棵 \(n\) 个点的以 \(1\) 为根的有根树，你需要选择若干条路径（可以有交）。
给定 \(m\) 个二元组 \((x,y)\)，表示需要存在至少一条路径经过 \(x,y\)，保证 \(x\) 是 \(y\) 的祖先。
求至少需要多少条路径。
保证 \(n,m \le 2 \times 10^5, \sum n, \sum m \le 5 \times 10^5\)。
如果选择若干个直上直下的路径的，那么很显然可以从儿子选到根节点。但这样显然不是最优的，于是考虑把这些路径在共同的上端合并成一个大路径。
先考虑下端。找出所有子树都没有限制下端的点，且自己是限制下端的点。可以发现这些点作为直上直下路径的下端一定不劣。
于是考虑上端怎么选来匹配这些路径。从下往上考虑每个点。
对于点 \(u\)，考虑他的子树有什么。(1) 当前路径没达到选择的二元组的上端深度。(2) 已经达到上端深度，尚未匹配。(3) 已经匹配的路径。
关于第一个路径。可以在目标深度上打标记。使往上判断时，到达标记的深度时，这些路径变为第二种路径考虑。
然后发现第二种和第三种可以互相转化。考虑合并两个子树 \(p,q\)，注意到如果我们把一个子树内的第三种路径拆开然后分别匹配另一个子树的路径，答案不会变。
不妨设 \(p,q\) 的第二种路径数为 \(x,y\)，第三种为 \(a,b\)。不妨设 \(x,y\)，把 \(x\) 向 \(y\) 匹配，然后再拆一点 \(a\) 来补剩下的。
子树合并后，考虑他自身。如果此时还有第一类路径，可以直接把他归到第一类路径的情况里。否则，找一个 \(2\) 或者拆一个 \(3\) 接上这个点，或者自身为一个新路径即可。
复杂度 \(\mathcal{O}(n + m)\)。
「AHOI2022」山河重整
计数有多少个元素在 \([1,n]\) 的集合，其 \(01\) 背包能表示 \([1,n]\) 中的所有数。
保证 \(n \le 5 \times 10^5\)。
考虑从小到大加入数，然后基于前面来判断值域的状态。然后发现这样他能表示的一定是一个前缀。于是考虑 DP，不妨设 \(f(i,j)\) 表示目前加入第 \(i\) 个数，然后当前值域为 \([1,j]\)，于是有 \(f(i,j) \leftarrow f(i-1,j-i)\)。
考虑这个东西怎么优化。发现寄。
接着发现，对于一个集合，他能拼出 \(k+1\) 需要集合中 \(\le k\) 的数的和 \(> k\)。于是可以容斥，考虑一个不合法的状态，也就是说对于 \(i\)，集合中小于 \(i\) 的数的和恰好等于 \(i\)。设 \(f(i)\) 表示集合为 \([1,i]\) 的数，能拼出 \([1,i]\) 的数，且集合元素的和恰好为 \(i\)。
转移的时候枚举首个不合法的位置。依然是 \(\mathcal{O}(n^2)\)。
但是恰好等于 \(i\) 让我们想到整数拆分，这个是 \(\mathcal{O(\sqrt{n})}\) 的。 于是反过来考虑，选 \(\sqrt{n}\) 个数，然后是他们的和为 \(n\)。于是转移的时候要么全局加一，要么只会改变 \(\sqrt{n}\) 个数。
于是复杂度 \(\mathcal{O}( n \sqrt{n})\)。
「ARC092B」Two Sequences
给你长度为 \(n\) 的两串序列 \(a,b\)。
求 \(a,b\) 两序列各任取一数相加形成的 \(n^2\) 个和的 \(\operatorname{xor}\) 和。
保证 \(1\le n \le 200000,0\le a_i<2^{28}\)。
自然想到拆位考虑。于是变成了求有多少组 \((i,j)\) 满足 \(a_i + b_j \bmod 2^k > 2^{k-1}\)。若有奇数组那这位答案是 \(1\)，否则为 \(0\)。
于是排序考虑二分。如果 \(a_i < 2^{k-1}\) 那么 \(2^{k-1} - a_i \le b_j \le 2^k - a_i -1\)，否则为 \(2^k - a_i \le b_j \le 2^k - a_i -1\)。
复杂度 \(\mathcal{O}(n \log n)\)。
「CF150E」Freezing with Style
给定一颗带边权的树，求一条边数在 \([L,R]\) 之间的路径，并使得路径上边权的中位数最大。输出一条可行路径的两个端点。
注：此处 \(1,2,3,4\) 的中位数为 \(3\)，而非 \(2\) 或者 \(2.5\)。
考虑二分答案。然后将 \(\ge \text{mid}\) 的边看作 \(1\)，\(<\text{mid}\) 看成 \(-1\)。如果存在一条 \(>0\) 的路径，那么说明存在 \(>\text{mid}\) 的权值的路径。
考虑点分治，统计路径然后单调队列维护合并。
「CF538G」Berserk Robot
有一个机器人，第 \(0\) 秒时在 \((0,0)\) 位置。
机器人会循环执行一个长度为 \(l\) 的指令序列，每秒执行一个指令。
指令有
ULDR四种，分别代表向上/左/下/右移动一格。你不知道这个指令序列具体是什么，但是你知道 \(n\) 条信息，第 \(i\) 条信息为「第 \(t_i\) 秒时机器人在 \((x_i,y_i)\)」，保证 \(t\) 递增。
你需要构造一个满足这些信息的指令序列，或判断不存在。
保证 \(n \le 2 \times 10^5\)，\(l \le 2 \times 10^6\)，\(t_i,|x_i|,|y_i| \le 10^{18}\)。
为什么只想到了后一半没想到前一半。
因为横纵坐标有关联，考虑旋转坐标轴。
将坐标轴旋转 \(45°\)，再翻倍 \(\sqrt{2}\)，信息条件为 \((x_i+y_i,x_i-y_i)\)。于是题目中的操作变成了 \((1,1),(1,-1),(-1,-1),(1,-1)\)。此时 \(x,y\) 修改已经独立。
再将信息条件加上时间除以 \(2\)，于是操作变成了 \((1,1),(0,1),(1,0),(0,0)\)。
观察题目这个周期，发现最后他是一个形如 \(kx+b = (x_i,y_i)\) 的形式。差分后分开解就可以了。
「CF538H」Summer Dichotomy
有 \(T\) 名学生，你要从中选出至少 \(t\) 人，并将选出的人分成两组，可以有某一组是空的。
有 \(n\) 名老师，每名老师要被分配到两个小组之一，对于第 \(i\) 名老师，要求所在的小组中的学生人数 \(\in [l_i, r_i]\)。
此外，有 \(m\) 对老师不能在同一个小组中。
你需要判断能否满足所有要求，如果可以，请给出一种方案。
保证 \(t \le T \le 10^9\)，\(n,m \le 10^5\)。
首先有，如果出现 \(3\) 个老师互相的交集为 \(0\)，那么就无解了。然后令 \(n_1 = \min\{ r_i \},n_2 = \max \{ l_i \}\)。表示两组的人数。
如果 \(n_1 \ge n_2\)，那么这意味着所有老师都两两有交集。那么就随意了。
否则 \(n_1 < n_2\)，那意味着一旦增大 \(n_1\) 或者减少 \(n_2\)，那么就会寄。这意味着如果我们要调整组员人数，只能减少 \(n_1\) 或者增大 \(n_2\)。
然后考虑 \(t \le n_1 + n_2 \le T\) 这个条件，多了就从 \(n_1\) 扣少了就从 \(n_2\) 补。然后根据这个条件对这个二分图染色一下就可以了。
「CF603E」Pastoral Oddities
给定一张 \(n\) 个点的无向图，初始没有边。
依次加入 \(m\) 条带权的边，每次加入后询问是否存在一个边集，满足每个点的度数均为奇数。
若存在，则还需要最小化边集中的最大边权。
\(n \le 10^5\)，\(m \le 3 \times 10^5\)。
首先这个条件是可以转化的，他的充要条件是该图只存在偶数点的连通块。证明略。
接着考虑最小化最大边，很自然想到从小到大加边，然后并查集维护连通块大小就可以了。
动态修改呢？首先可以想到线段树分治。
注意到一条边如果出现的时候没有加入答案边集，他就再也不会加入了。这意味着他只会影响一段时间区间。当我们加入一条边的时候，后移加边，知道答案合法。这段时间就是这条边影响的范围。
于是从右到左递归，得出每条边影响的区间。然后对于其影响的线段树分治的区间，加上这条边就可以了。
「CF613E」Puzzle Lover
给定一个 \(2 \times n\) 的矩阵，每个位置上有一个小写字母。
有一个长度为 \(k\) 的小写字符串 \(w\)，询问矩阵中有多少条有向路径满足以下条件：
- 路径上的字母连起来恰好为 \(w\)。
- 不多次经过同一个位置。
- 只能向上下左右四个方向走。
保证 \(n,k \le 2 \times 10^3\)，答案对 \(10^9+7\) 取模。
先称这条路径最左侧那列为左侧，最右侧那列为右侧。于是一条合法的路径可以拆成 \(3\) 个部分。
- 从某一列出发，先向左走到最左侧，然后向下 / 上后向右走。
- 从某一列出发，向下向上，但只向右走。
- 从某一列出发，向右走到最右侧，然后向下 / 上后向左走。
一和三可以通过哈希解决。考虑第二种情况，不妨设 \(f(i,j,k)\) 表示到 \((i,j)\) 匹配到 \(w\) 的第 \(k\) 个字符但是没有上下跳的，\(g(i,j,k)\) 同理但是有上下跳的。来回转移即可。
「CF708D」Incorrect Flow
给定一张 \(n\) 个点 \(m\) 条边的网络，源点为 \(1\)，汇点为 \(n\)。对于每条边，有容量 \(c\)，当前流量 \(f\)。但这个图是错误的，可能存在 \(c < f\)，或者流量不守恒的情况。
你每次操作可以将某条边的 \(c\) 或 \(f\) 加 \(1\) 或减 \(1\)。请你用最少的操作次数将图变成一个正确的网络。
保证 \(n,m \le 100\)，\(c,f \le 10^6\)，\(1\) 没有入边，\(n\) 没有出边。
如果 \(f \le c\) 那么我们只需要花费 \(1\) 的代价就能修改。否则就要花费 \(2\) 的代价。于是分类。
- 先是 \(f \le c\)。
- 减小 \(f\)，连边 \((v,u)\)，容量为 \(f\)，费用为 \(1\)。
- 增大 \(f\)，且 \(f \le c\)，连边 \((u,v)\)，容量 \((c-f)\)，费用 \(1\)。
- 否则 \(f>c\)，容量 \(+\infty\)，费用 \(2\)。
- 否则 \(f>c\)。同理不写了。
然后建立一个大 \(S\) 和 \(T\) ，如果一个点 \(u\) 的流量不守恒，就用这两个点调，和上下界网络流建图差不多。
「CF1120F」Secret Letters
有两个人，小 W 和小 P，他们俩打算相互送信。有两种方法送信。
有个地方 R，可以将信寄存在 R 这里（一个人只有在再一次去寄存信的时候才能拿走寄存在那里的别的人给他的信），寄存代价是每封信每个单位时间 \(c\) 的代价
可以直接花费 \(d\) 的代价直接送出。
一共送 \(n\) 封信，每次在 \(t_i\) 时，\(p_i\) 送信。最后，在 \(t_{n+1}\) 的时候，俩人都跑到 R 那里去喝茶，并拿走剩下的寄存的信。
保证 \(1\leq n \leq 10^5,1 \leq c \leq 10^2,1 \leq d \leq 10^8,0 \leq t_{i} \leq 10^6,t_i<t_{i+1}\)。
考虑一份信寄存。会花费 \(c \cdot (t_j - t_i)\)，最后一个会花费 \(c \cdot (t_{n+1} - t_i)\)。这意味着第 \(i\) 信寄存，后面的花费至少 \(c \cdot (t_{n+1} - t_i)\)。如果我们在这期间塞一些信进去，花费不变。
所以会选择花费大的去寄存，交替的时候选一下就行了。
「CF1131G」Most Dangerous Shark
我不好说。
不妨处理出 \(l_i,r_i\) 表示第 \(i\) 个骨牌向左 / 右推到最远可以推到的点。然后考虑 DP，设 \(f(i)\) 表示推倒前 \(i\) 个骨牌的代价。
转移枚举一个 \(j\)，表示推到 \(j \sim i\) 中的骨牌，有两种情况，一种是选择用 \(i\) 来推倒，那么显然在 \(l_i\) 处转移即可。
那么如果我们用 \(j\) 来推倒。有转移：
这东西因为 \(j\) 需要满足 \(j < i \le r_j\) 所以不是很好直接做。所以得去挖掘性质。
注意到 \(r_j \ge i\)，这意味着一定有 \(r_j \ge r_i\)，证明简单，略。
于是我们用一个单调栈，维护 \(f(j-1)+c_j\) 单调递增，并且此时一定满足 \(r_i\) 单调不降。
复杂度 \(\mathcal{O}(n)\)。
「CF1295F」Good Contest
\(a_i\) 在 \([l_i, r_i]\) 等概率随机，求 \(a_{1 \dots n}\) 单调不增的概率。
保证 \(n \le 50\)。
首先可以将概率转为求方案数。有一个暴力 \(f(i,j)\) 表示到 \(i\) 时，且 \(a_i = j\) 的方案数。转移显然。
但值域过大，寄。但也是因为值域比较大，中间一段其实都是求和的形式。类似一个分段函数。
于是离散化，不妨设 \(f(i,j)\) 表示到第 \(i\) 个时，\(a_i \in [j,j+1)\) 的方案数。于是复杂度问题解决。
「CF1372E」Omkar and Last Floor
一个 \(n\times m\) 的矩阵，初始值全为 \(0\) ，每一行都被分成若干部分，每一部分只能出现一个 \(1\) ，设 \(q_i\) 为第 \(i\) 列 \(1\) 的个数，求 \(\sum_{i=1}^mq_i^2\) 的最大值。
保证 \(n,m \le 100\)。
难点是想到区间 DP（。
对于一段区间，选出一列 \(k\)，然后尝试把他最大化贡献，然后去掉经过 \(k\) 的区间，然后问题变成了 \([1,k-1],[k+1,m]\) 两个问题。
DP 也是一样的，我们预处理一个 \(s(i,j,k)\) 表示在区间 \(i,j\) 范围内，经过了 \(k\) 这个位置的区间数量。然后直接转移即可。
「CF1420E」Battle Lemmings
有 \(n\) 个守卫排成一行，编号为 \(1\) 到 \(n\)。这些守卫里有的拿着盾牌，有的没有。一个守卫只能同时拿一个盾牌。称一对守卫是被保护的，当且仅当这两个守卫都没拿盾牌，但他们之间有守卫拿了盾牌。
每一秒，指挥官可以下达两种命令中的一种，分别是：
- 选一个带盾牌的守卫，把它的盾牌给他左边的守卫
- 选一个带盾牌的守卫，把它的盾牌给他右边的守卫
请求出时刻 \(0\) 到 \(\frac{n \times (n - 1)}{2}\) 中每个时刻最多有多少对守卫是被保护的。
考虑算对立面，计算 \(0\) 的连续段。然后如果已知目标状态，贪心选相邻的就可以算出操作数。
所以设 \(f(i,j,k)\) 表示第 \(i\) 位填 \(1\)，移动了 \(j\) 次，前面有 \(k\) 个 \(1\)，此时没被保护守卫的最小值。
复杂度 \(\mathcal{O}(n^5)\)。
「CF1439E」Cheat and Win
在二维坐标系上，考虑所有满足 \(x \text{ and } y = 0\) 的点 \((x, y)\)。若有两个这样的点相邻，就将它们连一条边。可以证明，这些一定会形成一棵树，不妨令其根为点 \((0, 0)\)。
树上的每个点可以被染成黑色或白色。给定 \(m\) 条链（可能相交），初始时这些链上的点均为黑色，其余为白色。
两名玩家在树上做游戏。每名玩家可以选择一个黑点以及它的祖先的子集，并将这些点反色，当无法选择时该玩家输。
后手打算作弊，他会在游戏开始前做若干次操作，使得他可以获胜。操作形如选择一个点，将其到根的路径上的所有点反色，最小化操作的次数。
保证 \(m \le 10^5\)，坐标的范围不超过 \(10^9\)。
先考虑必胜状态。如果一个局面的 \(\text{SG}\) 等于其中黑点的 \(\text{SG}\) 的异或值，后手必胜。然后因为深度为 \(d\) 的黑点的值为 \(2^d\)，所以如果每一个深度的黑点的个数都为偶数则后手必胜。
然后要把 \(m\) 条路径修改，建立虚树。然后发现这个树张的非常有规律，可以直接用分治来建树。
于是后手希望修改若干条路径使得每层黑点都变成 \(0\)。每个 \(1\) 连续段我们只需要 \(2\) 次操作就行，注意细节，如果是根节点，就需要一次。
「CF1446E」Long Recovery
平面上有一无穷大的坐标系，每个点 \((x,y)\) 和 \(3\) 个点相邻。对于 \(x\) 是奇数的情况相邻点的坐标是 \((x\pm1,y)(x-1,y+1)\)，否则就是 \((x\pm 1,y)(x+1,y-1)\)。
每个坐标可能是黑点或白点之一，每秒整个坐标系会发生如下两种操作之一。
对于一个有两个相邻黑点的白点，白点变成黑点。
对于一个有两个相邻白点的黑点，黑点变成白点。
注意即使有多个点满足能改变颜色的条件，每秒也只会有一个点改变颜色。
我们希望黑色点能尽快变成白点。给定 \(n\) 个黑点的坐标，在最坏情况下是不是存在一种变色方案使得黑点会永远存在，如果是，输出
SICK。否则输出RECOVERED并求在最坏情况下将所有黑点变成白点需要用的最短时间。
画图，（因为懒的画图所以尝试用言语描述）如果出现一个黑色的环，那么一定是无解。然后我们将图尽量染黑，如果染黑后的图出现了黑环，那么也一定无解。
不妨设 \(p\) 为不同颜色相邻格子的数量，如果修改一个格子，只会有减去 \(3\) 和减去 \(1\) 两种情况。
我们希望第一个操作尽量少。然后我们发现当不能使用操作二的时候才会选择操作一，所以这意味着如果他长成这样：
于是记这个东西的数量为 \(q\)，再设连通块有 \(d\) 块，则有答案 \(p -2d - 2q\)。
「CF1517G」Starry Night Camping
有 \(n\) 顶帐篷,第 \(i\) 个帐篷位于 \((x_i，y_i)\)点上，重量为 \(w_i\)。当且仅当 \(x_i\)和 \(y_i\)都是偶数时，帐篷才是重要的。您需要移除一些帐篷，以便对于每个剩余的重要帐篷 \((x，y)\)，不存在另外 \(3\)个帐篷 \((x'_1，y'_1)、(x'_2，y'_2)和(x'_3，y'_3)\)，使得这两个条件都成立：
\(|x'_j-x|，|y'_j-y|\le 1\)，所有 \(j\in\{1，2，3\}\)。
这四个帐篷形成一个平行四边形(或矩形)，它的一条边平行于x轴。
请将未移走的帐篷重量之和最大化。打印最大值。
保证 \(n \le 1000, |x_i|,|y_i| \le 10^9\)。
考虑对 \(x,y\) 分奇偶 \(0,1\)，于是一个不合法的平行四边形可以表示为 \((1,1) \rightarrow (0,1) \rightarrow (0,0) \rightarrow (1,0)\)。
那么问题就是删除若干个点，使得图中不存在这样的路径。
考虑最小割。然后拆点，一个点拆成两个 \(u_{i,1} \rightarrow u_{i,2}\) 边权为 \(w_i\)。剩余点正常连，边权为 \(+\infty\)。
「CF1620F」Bipartite Array
定义一个数列是
二分的，当且仅当用以下方法构造一张无向图，该图是一张二分图：
- 这张图有 \(n\) 个从 \(1\) 编号到 \(n\) 的节点
- 对于且仅对于所有满足 \(i < j,a_i>a_j\) 的数对 \((i,j)\)，在 \(i\) 号节点和 \(j\) 号节点间连有一条无向边。
定义一次
操作为将某个 \(a_i\) 变为它的相反数，现给你一个长度为 \(n （n\leq 10^6）\) 的排列，要求你判断是否可以通过有限次操作使该排列变为二分的数列。若无可行方案，输出
NO，否则输出YES，并输出任意一个通过操作变为的二分的数列。
因为二分图不存在奇环。所以我们直接考虑奇环。这张图可以证明如果存在奇环则一定存在大小为 \(3\) 的奇环。
于是将原始序列拆成 \(2\) 个单谷序列即可。DP 即可。
「HNOI2019」鱼
给定 \(n\) 个坐标，求六元组构成鱼的数量。鱼的定义点链接。放个图。
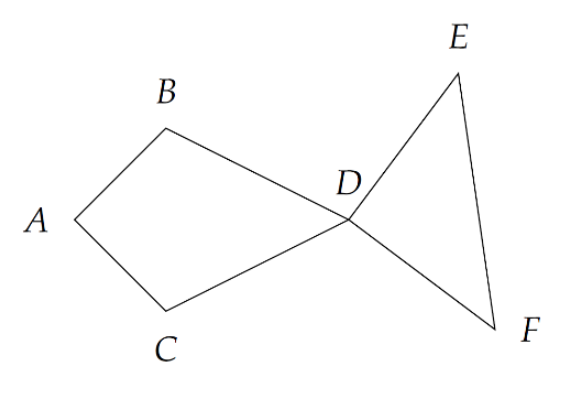
保证 \(n \le 10^3,|x|,|y| \le 10^9\)。
首先可以想到枚举 D 点。对于每个点处理出鱼头，鱼身，然后再合并算。
枚举 D 点，剩下点按照极角序排序，然后枚举 A 点，此时可以开双指针维护合法的 E,F 点，用 map 存储他们到 D 的距离方便计算方案数。
然后考虑 B,C 的情况。首先有 \(BC \perp AD\)。所以从斜率方向入手，先预处理出每一条线的斜率，然后按照中点所在位置分类。这样就可以找到合法的 B,C 了，然后二分长度，使题目要求的角是锐角即可。
复杂度 \(\mathcal{O}(n^2 \log n)\)。
「NEERC2016」Binary Code
给定
n个 01 串，每个字符串至多有一位是未知的，可以填0或1，求是否存在一种方案，使得任意一个字符串不是其它任意一个字符串的前缀。保证 \(n \le 5 \times 10^5\)。
首先注意到如果一个串选择了一个 \(0\) 或者 \(1\)，会对其他串有一个约束。这自然联想到 2-SAT。直接 \(\mathcal{O}(n^2)\) 枚举其实不大行，\(n\) 个串想到字典树，于是考虑在字典树上建边。
一个点选定后，就不能选他前缀上的点，于是考虑另建一列点来表示前缀，于是建图就是和一个前缀连边，边降到 \(\mathcal{O}(n)\)，可以通过本题。
题外话：我就是这题写完然后打的某场模拟赛，我 T1 写个网络流前缀优化建图很合理吧。
「NWRRC2016」Integral Polygons
按顺序给定一个凸多边形的 \(n\) 个定点 \((x_i,y_i)\) ， \(x_i,y_i\in[-10^9,10^9]\) 且为整数。
求满足条件的对角线数量，使得该对角线将多边形分成的两个部分的面积皆为整数。
保证 \(n \le 2 \times 10^5\)。
想到叉积。因为有一个除以二，所以如果最后是奇数就一定带小数。所以我们只要考虑奇偶性即可。
然后用桶存一下，\(\mathcal{O}(n)\) 算。
「NWRRC2017」Equal Numbers
给定一个长度为 \(n\) 的数列 \(a_1,a_2,a_3,...,a_n\)，每次操作，你可以让某个被选定的数乘上任意一个正整数。
现在。对于所有的 \(k\in[0,n]\)，求出经过 \(k\) 次操作后数列里面不同的数的数量能够达到的最小值。
保证 \(n \le 3 \times 10^5,1 \le a_i \le 10^6\)。
首先一个数操作一次就行了。且只有两种选择，变成所有数的最小公倍数 \((1)\)，或者变成某个在原数组中出现过的倍数 \((2)\)。我们把这些数分成这两种情况。
先考虑 \((1)\) 的情况，显然，对于一种数，我们需要将和他相同的所有数都修改，否则答案不会改改变。
再考虑 \((2)\) 的情况，第一步首先肯定会增加一个数，然后就是和上面一样，修改了几类数就少几个数。
容易证明，\((1),(2)\) 同时操作不如全部操作 \((2)\)。
「SDOI|SXOI2022」小 N 的独立集
给定 \(n\) 个点的树的形态以及点的权值 \(v_i\) 范围 \(k\)，对于任意 \(i \in [1,kn]\)， 求有多少种权值分配方案，使得树的最大权独立集大小为 \(i\)。
满足 \(n \le 1000,k \le 5,u_i,v_i \le n\)。
首先有一个暴力，枚举所有点的点权，然后做一个独立集的 DP。
注意到 \(k\) 非常小，说明 \(f(u,0/1)\) 的答案也不大，于是将答案作为状态。于是不妨设 \(g_{u,v_0,v_1}\) 表示点 \(u\) 的的 \(f_{u,0},f_{u,1}\) 的答案为 \(v_0,v_1\) 时，的方案数。于是转移的时候枚举儿子的答案即可。
复杂度 \(\mathcal{O}(n^4k^4)\)，剪一剪可以过部分分。
然后发现不好优化。状态太多。所以从最开始 \(f\) 思考是否能优化。
不妨设 \(f(u,0/1)\) 表示 \(u\) 子树内是否强制不选 \(u\) 的方案数。然后他有一个性质 \(0 \le f(u,0) - f(u,1) \le v_u \le k\)。于是设状态 \(g(u,v_1,d)\) 表示 \(u\) 的 \(f(u,0)=v_1+d,f(u,1)=v_1\) 的方案数。其中 \(d \le k\)。
复杂度 \(\mathcal{O}(n^2k^4)\)，剪一剪可以过。
「SDOI | SXOI2022」整数序列
给定序列 \(a,b\)，\(q\) 次询问两种颜色 \((x,y)\)，定义一个区间的权值为其中 \(a\) 值为 \(x\) 或 \(y\) 的 \(b\) 值之和，求 \(x\) 数量等于 \(y\) 数量的子区间权值最大值。
保证 \(n \le 3 \times 10^5,q \le 10^7\)。
考虑根号分治。
先想暴力，可以把当前颜色取出来，对这个区间线性做一下就好了。实时维护一个数组 \(p\)，其中 \(p_x\) 表示两个颜色的差值为 \(x\) 时，各删掉一个前缀后的最小代价。和答案一起更新就可以了。
于是对于出现次数 \(c_i < B\) 的颜色可以直接暴力做这个。对于 \(c_i \ge B\) 的也可以跑这个暴力，注意到这些颜色最多只有 \(\dfrac{n}{B}\) 个，于是可以加个记忆化。
然后考虑一个颜色 \(<B\) 一个 \(\ge B\) 的情况。不妨设 \(c_x < B,c_y \ge B\)，注意到会存在一个连续的 \(y\) 区间，他长度大到已经无法满足条件，可以把这种区间缩起来。
于是维护一个 \(y\) 的位置坐标，对于非常长的区间，维护前 \(c_x\) 个和后 \(c_x\) 个即可维护答案。
「SNOI2020」取石子
甲乙两个人玩取石子游戏。他们面前有一堆共 \(n\) 个石子，然后由甲先手，两人轮流从中取走石子：甲第一次取走的个数不能超过 \(k\)，接下来每个人取走的个数不能超过上一个人刚刚取走个数的 \(2\) 倍。每人每次必须至少取一个石子。取走最后一个石子的人失败，另一方获胜。
现在已知 \(k\)，请你求出在 \(1\) 到 \(N\) 中有多少整数 \(n\) 使得甲在 \(n\) 颗石子的游戏中有必胜策略。
保证 \(T \le 10^5,N,k \le 10^{18}\)。
学习新知识（1/1）。
如果不看 \(k\) 那么这是一个斐波那契博弈（Fibonacci Nim）。以下会省略大部分证明。
这个时候当且仅当 \(n\) 是斐波那契数的时候先手必败，否则先手必胜。并且后手最后一次取的数量 \(\le \frac{2}{3}n\)。
齐肯多夫定理：任意正整数都可以被拆分为若干个斐波那契数之和。
然后回头考虑这道题。
首先如果 \(n\) 是斐波那契数，先手还是必败。于是考虑非斐波那契数。不妨设 \(n = \sum\limits_{i} fib(p_i)\)。
如果 \(fib(p_1) > k\) 则先手必败。因为这意味着第一回合先手没法去完 \(fib(p_1)\)，于是第一回合的问题就是一个斐波那契博弈，一个大小为 \(fib(p_1)\) 的问题。于是就给了后手一个必胜的机会。
所以问题就变成了下面这个，其中 \(\text{lowbit}\) 表示是齐肯多夫定理出来的最小项。
数位 DP 即可。
「ZJOI2022」树
我们构建两棵树，构建方法分别是：
第一棵：根是 \(1\)，对于 \([2,n]\) 中的节点 \(i\)，向 \([1,i-1]\) 中的一个节点连边。
第二棵：根是 \(n\)，对于 \([1,n-1]\) 中的节点 \(i\)，向 \([i+1,n]\) 中的一个节点连边。
称一种方案是好的当且仅当对于第一棵树的一个非叶子节点，它是第二棵树的叶子节点；对于第二棵树的非叶子节点，它是第一棵树的叶子节点。
给出 \(n\)，对于所有 \(i \in [2,n]\) 回答有 \(i\) 个节点的好的方案有多少，答案对 \(m\) 取模。
保证 \(n \le 500\)。
对于一个叶子的集合 \(S\)，他的答案是他所有点的前 / 后缀中非叶子的个数的积。
如果设第一棵树的非叶子节点为 \(S\)，那么第二棵树的非叶子节点 \(T\)。那么最后两棵树一定满足 \(S \cap T = \varnothing, S \cup T = \{ 1,2,\dots, n \}\) 两个条件。答案就是 \(S\) 和 \(T\) 的方案数的积。
考虑容斥，记 \(f(S)\) 的所有子集的非叶子节点构造的第一棵树的方案数。然后 \(g\) 同理。
于是有答案
注意到此时 \(s,t\) 不满足第二个条件，会出现部分元素不出现在 \(s\) 也不出现在 \(t\) 中。枚举他在 \(S\) 或 \(T\) 中即可。于是有：
接着考虑 DP。不妨设 \(f(i,j,k)\) 表示当前决策到 \(i\)，\(|s \cap \{ 1,\dots, n \} | =j,|t \cap \{ 1,\dots, n \} | =k\)。分类讨论一下，然后第一位滚掉就可以了。
- 如果 \(i \in s\) 则 \(f(i,j+1,k) \leftarrow f(i-1,j,k) \cdot j \cdot k\) 。
- 如果 \(i \in t\) 则 \(f(i,j,k-1) \leftarrow f(i-1,j,k) \cdot j \cdot k\)。
- 如果 \(i \notin s, i \notin t\) 则 $f(i,j,k) \leftarrow - 2 \cdot j \cdot k \cdot f(i-1,j,k) $ 。
复杂的 \(\mathcal{O}(n^3)\)。
「ZJOI2022」众数
给定一个长度为 \(n\) 的序列，你能对它进行一次区间加，最大化众数出现次数。
满足 \(t \le 20, 2 \le n \le 2 \times 10^5,a_i \in 10^5, \sum n \le 5 \times 10^5\)。
首先考虑选择一个子区间，把里面最多的颜色改成外面最多的颜色。
于是对颜色大小 \(s_i\) 根号分治。
对于出现次数 \(\ge \sqrt{n}\) 的颜色，暴力处理每个前缀和出现的每个颜色的次数，然后可以直接快速得到一个区间某颜色的次数。然后枚举两个数 \(x,y\)，讨论一下 \(x\) 在外的情况，然后对于 \(y\) 的一段区间的贡献为 \(s_y-s_x\)，就是最大子段和。复杂度是 \(\mathcal{O}( n \sqrt{n})\)。如果其中一个颜色不满足 \(\ge \sqrt n\) 也同理。
考虑次数 \(< \sqrt{n}\) 的颜色。此时两个颜色都满足这个条件。考虑枚举区间。但这样会寄。于是对于每个左端点，预处理出一个颜色出现次数 \(1 \sim s_i\) 的最小右端点。然后枚举颜色，枚举去掉的区间即可。复杂度 \(\mathcal{O}(n \sqrt {n})\)。
「2022-10-09 提高模拟赛」
异或 (xor)
首先注意到选多个数和一个数是等价的。于是可以枚举选哪个数，然后取答案最大值，复杂度 \(\mathcal{O}(n^2)\)。
考虑拆位，记录 \(n\) 个数第 \(i\) 位有 \(cnt_i\) 个 \(1\)，有 \(n-cnt_i\) 个 \(0\)。
于是如果异或一个第 \(i\) 位 \(1\) 的，这位的贡献为 \((n-cnt_i) \cdot 2^{i}\)，反之亦然。
复杂度 \(\mathcal{O} ( n \log a_i)\)。
方块 (tetris)
这道题只有一步但是我就是没想到。我是小丑。
正着做不好做，于是考虑倒着做，每次枚举哪个方块可以移出去，判断是否能移出去就暴力 bfs 就行了。
复杂度 \(\mathcal{O}(n^6)\)。
会议 (meeting)
Source：「JOISC 2021 Day 3」聚会 2。
首先注意到，对于奇数个点，答案一定是 \(1\)。如果为偶数，那么最后的形式一定是，两颗大小为 \(\frac{i}{2}\) 的子树连起来中间链的长度。
所以只要是两颗满足 \(\ge \frac{i}{2}\) 的子树，就可以作为 \(i\) 个点答案。
考虑点分治。对于点 \(u\)，每次跑出当前子树大小为 \(sz\) 的最长链的长度。然后取个后缀最大值，合并两个链作为答案即可。
复杂度 \(\mathcal{O} ( n \log n )\)。
饮水 (water)
Source：「JOISC 2017 Day 3」长途巴士。
考虑 DP。但对于 \(s_i\) 不是很好做，于是考虑对 \(d_i\) 做。所有乘客对 \(d_i\) 排序，设 \(f(i)\) 表示前 \(i\) 个人的最小费用。
首先第一种情况，就是不赶第 \(i\) 个人，让他一直喝。
然后考虑如果要赶走若干个人的情况。注意到如果要赶走，赶走的一定是以某个加水服务 \(s_i\) 前的一段后缀。所以如果 \(i\) 需要被保留，他之前的某个人 \(x\) 在某些时刻也必须保留下来，因为会出现 \(x\) 打水时没有水后离去，此时 \(x,i\) 之间没有加水点，于是导致 \(i\) 也离去的情况。
枚举 \(j\)，表示让 \(j+1 \sim i\) 的乘客下车。不妨设 \(mn_i\) 表示走到某个特殊的加水点时，\(j+1 \sim i\) 的所有人至少喝水的次数。
于是设 \(mn_i = \min \{ \left\lfloor \dfrac{s_j}{T} \right\rfloor \}\) 其中 \(s_j \bmod T \in [d_i,d_{i+1}]\)。设 \(sum_i\) 表示 \(c_i\) 的前缀和。所以
然后这个东西是可以斜率优化的。
于是有斜率 \(mn_i\)。单调栈维护，二分选择斜率。
「2022-10-13 提高模拟赛」
很担心组题人的精神状态。
密室 (sanctum)
首先前 \(k\) 个数必须和 \(1\) 连通，后 \(n-k\) 个数不能和 \(1\) 连通。意味着两部分没有关联，分开考虑。
后 \(n-k\) 数的方案数显然为 \((n-k)^{n-k}\)。
前 \(k\) 个数，因为注意到 \(2 \sim k\) 都和 \(1\) 连通，于是 \(1\) 随意即可，即 \(k\) 种。接下来问题就变成了生成一棵 \(k\) 个点的树，根据 \(\text{prufer}\) 序列可以得知答案为 \(k^{k-2}\)。
于是最后答案为 \(k^{k-1} \cdot (n-k)^{n-k}\)。
数学 (math)
赛时打表发现答案为 \(2 \cdot \min(k,n-k+1)\)，然后 \(n=1\) 特判。考虑证明。
首先对于 \(n=1\) 答案一定是 \(1\)。对于 \(k=1\)，首先让两条线的交于最低一点，剩余的线与这两条的交点一定高于这个最低的点。于是一定有答案 \(2\)。
对于构造的第 \(k\) 层，若他的答案为 \(ans\)，那么我们将整个图上下翻转，于是可以得出 \(n-k+1\) 层的答案为 \(ans\)。
那么我们只考虑 \(2k \le n\) 的情况。
对于 \(k>1\) 的情况，不妨假设答案为 \(2\cdot (k-1)\)。然后考虑第 \(k\) 层。
第 \(k-1\) 层的 \(2 \cdot (k-1)\) 段线会继续往上方向延伸。这意味着在上方这几段线一定会产生新的交点。而题目中要求一个交点只能由两条线组成，这意味着会有一条新的线会穿过这些延伸上的线，形成新的 \(2 \cdot (k-1)\) 个交点。这是这个新的线会产生两段的贡献在第 \(k\) 层的最左和最右边。
于是第 \(k\) 层的答案为 \(2k\)。得证。
函数 (function)
首先这东西上来给人的感觉就很凸包。于是考虑 \(b,c\) 的值怎么求时，可以发现这个二次函数可以转化为一次函数。
简单移项一下，于是有 \(y-x^2 = bx + c\)。那么不妨将初始的所有坐标都改成 \((x,y-x^2)\)。那么问题就变成了，任意选两个点，过这两个点的一次函数的上方不能有任何点。
然后发现这就是求一个上凸壳。而函数的答案就是凸壳的边数。当然，对于 \(x\) 相同的点，取 \(y\) 最大值就可以了。
复杂度 \(\mathcal{O}(n \log n)\)。
以下是文学废物瞎扯的内容。就看着乐吧。但是这个对联我想的比这道题做法还久。
然后我们考虑题目中那个故事的对联。「星河」、「醉」与「梦」。第一个和最后一个都是名词，而关于「醉」，我个人理解为一种状态「醉着」，但又可以理解为动词「沉醉」。而题目中另一句可以推测出，「醉」更偏向于动词，但当然这里可以自由一些，根据最后的意境来决定。
「星河」是两名词合为一的物，我联想到了「花海」。「星」与「花」，「河」与「海」都是意境很相似的一物。
有了地点，接着想后两个字。这两个字必须有一种联系。「花海」中联想到了「舞」，「醉」又联想到了「饮」。两者都是动词，当然「舞」似乎也可以为一种「在起舞」的状态。
最后一物，因为上半句的一种很明显的感觉是，追梦，醉梦。陶醉，但却孤独，又有一种无奈的悲感。根据此来取最后一字。「花海」联想到「蝶」，而此时的意境也能想到「月」。结合一下前面取的词，「对饮成三人」似乎很适合这个情景。但此时我突然觉得上下句重复情景不太好。于是第二字决定取「舞」。
「舞」似乎更适合「蝶」。但「蝶」比「月」少了一种孤独感。「月」只有一个，但「蝶」可以许多。「对饮成三人」的月正是体现了这种感觉。且结合「梦」的平仄为去声，「月」也同为去声。故最后取「月」。
我心沉醉于遥远星空的梦，我身独舞与花海上星辰的明月。
「星河醉梦，花海舞月。」
烧饼 (pancake)
你先别急。
「2022-10-14 提高模拟赛」
录像 (tv)
你说的对。但是我赛时写网络流，首先有一个很显然的建图，对于一个动漫，向后与和他不重叠的动漫连边，流量 \(1\) 费用 \(0\)。然后减一个超级源点向所有动漫排序，流量 \(1\) 费用 \(1\)。每这样是边 \(\mathcal{O}(n^2)\)。显然跑不过。
然后我们发现如果我们对 \(x\) 排序，每个动漫所连边一定是一个后缀，于是我们做一个后缀的连边优化。这样边数是 \(\mathcal{O}(n)\) 的了。虽然这样还是 T 了（。
好了正经做法。
考虑贪心。我们用 set 维护录像带所录视频的列表。对于所有动漫按照 \(y_i\) 排序，依次判断。
如果此时 set 维护的数量不超过 \(k\)，那么直接将当前第 \(i\) 个录像加入即可。
否则，找出 set 中满足 \(y_j \le x_i\) 的最大 \(y_j\)，弹出他，加入最新的 \(i\)。
可以发现这样操作，每次答案一定不会变劣。
复杂度 \(\mathcal{O}(n \log n)\)。
能量骰子 (dice)
原题某句话：如果存在一枚正能量骰子和一枚负能量骰子点值的和为 \(0\)，它们会结对消失。
Linshey：连骰子都结对子了，不会还有人没有结对子吧。
我：你。
考虑 DP。不妨设 \(f(k,i,j)\) 表示要需要投 \(i\) 个正骰子和 \(j\) 个负骰子，且此时已投出的绝对值大于等于 \(k\)，的答案方案数。
于是最后的概率为 \(\dfrac{6^{a+b}-f(t,a,b)}{6^{a+b}}\)。
转移时候用 \(g_{j'}(i,j) = f(k+1,i,j') \times \dbinom{j}{j-j'}\) 降低复杂度即可。
退休计划 II (king)
很厉害。
首先考虑一棵树的情况。有一种构造很合理，假设选到 \(u\)，我们选择一个儿子 \(v\) 继续路径，使得左右两边数量尽量平均。可以证明到最后的时候一定存在方案使得左右两块数量相等。
考虑图，发现如果是 dfs 生成树，返祖边没有任何影响。所以正常做即可。
回家 (backhome)
鸽。
「2022-10-17 提高模拟赛」
三角计数问题 (triangle)
正着不好算，考虑容斥。于是计算的三角形一定满足存在 \(2\) 个同色。
于是枚举一个点 \(u\)，计算从他出发的两条边为一黑一白的数量。于是得到的总数除以二就是不满足同色的三角形的数量。用总数减去即可。
棋盘染色问题 (color)
什么 6g。
对于任意一个矩形，只要他存在 \(3\) 个点，我们就不需要画代价去填第四个点了。倘若把坐标拆开，不妨设矩形为所有坐标涉及的为 \(x_1,x_2,y_1,y_2\)。若 \(x_1,x_2\) 和 \(y_1,y_2\) 之间的连边为 \(3\) 条，那么这个矩形就填完了。
接着发现，连边恰好为 \(3\) 条的情况当且仅当这四个点不存在环。那么最后就是一棵树，于是横纵坐标拆开，连边的边权为格点的点权，然后跑最小生成树即可。
每日被卡常 (1/1)。预处理的时候取膜多加了 \(2\) 然后光荣 TLE。
石子合并问题 (stone)
首先他有一档 \(n \le 20\) 的部分分，暴搜即可。
然后总数据范围是 \(n \le 35\)，所以考虑双搜，搜完后，因为此时只要合并 \(2\) 个序列，且每个序列的数满足 $ < m$，那么对于两个数 \(x,y (x>y)\)，答案 \((x+y) \bmod m\) 一定劣于 \(x\)。所以两个序列可以双指针合并。
随机游走问题 (wander)
学弟直接找规律爆切。我被薄纱。
首先不妨设第 \(n\) 秒走到点 \(i \in [-n,n]\) 的概率为 \(p_i = \dfrac{\binom{2n}{n+i}}{2^{2n}}\)。一步拆两步，于是注意到呆在原地不动的概率和左右各走一次的概率是一样的。
然后由于
所以
由 \(\dbinom{n}{m}=\dbinom{n}{n-m}\) 把两项拆开。
预处理即可。复杂度 \(\mathcal{O}(n)\)。
「2022-10-18 提高模拟赛」
分配 (distrib)
首先有一个显然的建图。对物品 \(i\) 向人 \(j\) 连容量为 \(b_j\)。源点 \(s\) 向每个物品 \(i\) 连 \(a_i\)，每个人 \(j\) 向汇点 \(t\) 连边。答案就是最大流。显然会 T。
最大流转最小割。不妨假设我们要将物品集合 \(A\) 割给 \(S\)。于是对于一个人 \(i\)，割给 \(S\) 的代价是 \(c_i\)，割给 \(T\) 的代价是 \(|A|b_i\)，注意到这只和 \(A\) 的大小有关。所以这个完全独立了，枚举 \(A\) 的大小，然后排序选最小值即可。
求和 (sum)
若对每一块进行考虑，那么对于一个有 \(n\) 个点 \(n\) 条边的块，也就是基环树或环来说，里面一定不会存在 \(a_i=-1\)。否则就是一棵树了，那么也最多只会有一个 \(a_i=-1\)。
这意味着 $a_i =-1 $ 所在的连通块一定是树，剩下的一定是环或基环树。且这些环或者基环树的贡献一定不会变，可以先加上。
于是只要考虑是树的块。首先如果树中的 \(-1\) 连向了一个环或者基环树，那么当前情况的贡献 \(f\) 是不变的。不考虑。所以只考虑树和树之间。
一棵树也只有一个 \(-1\)，因此考虑将一个树看成一个点。于是设 \(g(j)\) 表示选若干个点合并成一个大小为 \(j\) 的环的方案数。
转移显然有 \(g(j) \leftarrow g(j-1) \times sz_i\)。因为点 \(i\) 都是内部连边，会贡献一个新的连通块。最后算一下贡献就好了。
滑动 (slide)
寄。
排列 (arrange)
考虑如何建图。对于每个速度都建立一个点，然后对于每个车，将 \(s_i \rightarrow t_i\)，然后建立虚点，虚点向最小值连边，最大值向虚点连边。然后每个时间点相邻直接由小到大连边权为 \(0\) 的边。对于 \(\max\{ t_i- s_{i+1} \}\) 的贡献，对于相邻的两个时间点，由大到小连边，边权为两点的速度差。
然后我们就得到了一个求最小哈密顿回路的问题。然后这是 NPC 问题。于是发表论文和改变建图二选一。
对于所有车站的 \(s_i \rightarrow t_i\) 的边是必走的，那对于相邻的边，我们不妨先不连。如果最后能做到恰好走过每一条边，问题就能从最小哈密顿回路变成欧拉回路问题。
于是考虑相邻点 \((i,i+1)\) 的边什么时候需要连上去。如果覆盖了这条边的边，向左向右不一致，我们就需要加上这条边。做个差分，如果左向多，则就是添加从小到大的 \(0\) 正向边，否则就是从大到小的，边权为速度差的反向边。
然后考虑连边后必须是连通图。于是对于相邻块连边即可，每次连一条正向和一条反向边。于是对于块内的每一个点，找到他最近的和他非一块的点，连边即可。最后跑最小生成树。
于是答案就是这张图的所有边的边权和。
「2022-10-21 提高模拟赛」
道路 (road)
最小瓶颈路。跑 \(\text{kruskal}\) 即可。
矩阵 (matrix)
神仙构造。还没订正，待补。
序列 (sequence)
先考虑如果 \(X,Y\) 有公共字串的情况。不妨设 \(X,Y\) 的最长公共子串为 \(S\)。
于是显然有一种方法，先将 \(X\) 一直删，直到剩下 \(S\)，然后再添加补成 \(Y\)，这样操作数是 \(|X| + |Y| - 2 |S|\)。
求最长公共子串可以用 SA，复杂度 \(\mathcal{O}(n \log n)\)。
但是题头是提高模拟赛（？），所以考虑不用 SA。考虑哈希，然后二分一个长度，枚举 \(X\) 该长度的子串，然后用 map 存下 \(Y\)，匹配即可。复杂度 \(\mathcal{O}(n \log^2 n)\)。
然后考虑没有公共字串的情况。这意味着 \(X,Y\) 没有相同字符。
有一个贪心。
如果 \(X\) 和 \(Y\) 没有公共字串，并且 \(|X| \ge 2\) 时，优先执行删除操作一定不劣。
根据这个贪心，我们可以一直删 \(X\)，直到 \(|X|=1\)，然后再加一个字符。如果依然没有公共串，那么就再删一个字符。
于是当 \(X,Y\) 有公共字串的时候，一定是长度为 \(1\) 的串。那么有公共串后就变成上面那个问题，答案为 \(|X|+|Y|-2\)。
然后问题就是最后选哪个字符为公共串。考虑建图，对于 \(A\)，将相邻的两个点连一条边权为 \(1\) 的边。于是问题就是以 \(A\) 中所有出现在 \(X\) 的字符为起点，以 \(A\) 中所有出现在 \(Y\) 中的字符为终点，求最短路。直接 bfs 即可。
最短路跑出来的最近的公共字符点中的路径，是要先加进来再删掉的，所以操作数为路径长度的 \(2\) 倍。
那么为什么这个贪心是正确的？
，因为不存在公共串，所以最开始出现在 \(|X|\) 的串中的字符一定是要被删掉的。然后我们会找到一个最近的公共字符的位置 \(p\)，即使我们先不删除 \(p\) 到原先串之间的路径，之后也需要删除到只剩下公共串，也就是位置 \(p\)。
但是否会出现串到位置 \(p\) 之间的字符出现，先被删，再加进来搭路到 \(p\)，再删掉的情况？可以发现，如果存在这种情况，那么这个操作数一定不是最短路径。
复杂度 \(\mathcal{O}(n \log n)\)。
序列 (sequence)
首先自然想到差分，于是一次修改变成加一个数减一个数。我们需要将所有数变成 \(0\)，对于一个数 \(c\)，可以列出式子 \(ax+by = c\)。所以如果 \(c \not| \gcd(a,b)\) 时，无解。然后我们有通解 \(x=x_0+ k \cdot \dfrac{b}{\gcd(a,b)},y=y_0+ k \cdot \dfrac{a}{\gcd(a,b)}\)。
因为要保证操作数 \(|x|+|y|\) 最小，于是对 \(x,y\) 分类一下，对比这几种情况取最小即可。
但是我们修改必须同时选择 \(2\) 个数，一加一减。考虑合法性。这意味着我们要保证 \(\sum |a| =0,\sum |b| =0\)。
但是因为那个方程，所以如果 \(a\) 满足条件，那么 \(b\) 也一定能满足条件。
每次找出 \(x,y\) 中 \(>0\) 的部分。然后将 \(x\) 减少 \(\dfrac{a}{\gcd(a,b)}\)，将 \(y\) 减少 \(\dfrac{b}{\gcd(a,b)}\)，大根堆维护反悔贪心即可。
「2022-10-24 提高模拟赛」
连通 (connected)
Source：「JOISC 2016 Day 3」电报
其实题目就是要求最后变成一个环。所以我们只要删掉到一条链，然后接起来就好了。
这意味着每个点只要保留一条边，保留一条最大的入边，为了防止有环，可以环上一点先断开。然后在做这个问题。
积木 (block)
Source：「JOISC 2019 Day 4」蛋糕拼接 3
首先有一个显然的贪心，如果我们已经选定好了蛋糕，那我们按照 \(h_i\) 排序的贡献一定最大，为 \(2 \cdot (h_{\max} - h_{\min})\)。
考虑把 \(h\) 排序离散一下，枚举 \(h\) 的上下界，也就是一段区间，然后因为 \(\sum v\) 要尽量大，所以求这个区间里 \(v\) 的前 \(k\) 大的和就可以。这个可以用主席树维护。
复杂度 \(\mathcal{O}(n^2 \log n)\)。
然后这东西有决策单调性，于是用分治来找决策点。复杂度 \(\mathcal{O}(n \log ^2 n)\)。
路径 (path)
Source：ARC118E Avoid Permutations
反过来求，求一条路径有多少不同的 \(P\) 使得改路径合法。设此时一定钦定了 \(k\) 个障碍。最后计算答案的时候容斥计算即可。
设 \(f(i,j,k,0/1,0/1)\) 表示走到 \((i,j)\) 钦定了 \(k\) 个障碍，第 \(i\) 行，\(j\) 列是否存在障碍。然后转移直接从上一步转移，然后对 \(k\) 分类讨论即可。
直径 (diameter)
订正是订正了。但写不动了（悲。看着可能会补一下？毕竟这题很厉害。
