「二分图」学习笔记
前言
如果有逻辑/语言不清楚或者错误的地方欢迎私信/评论教我语文。
这段时间一直在口胡二分图的东西,感觉这个知识点好多。挖个坑把自己埋了,看看能不能填完 ,或者说能填多少。
你会发现每次编辑时间跨度非常大(),所以每次编辑的时候语言风格可能略有差异。
因为有一些证明实在不会证,确实参考了网络上的东西。
- 开坑时间:\(\text{2020/03/29}\)。以下时间线指每次编辑结束时间。
- 第一次编辑:\(\text{2020/04/06}\)。判定、最大匹配、\(\text{k} \ddot{\text{o}} \text{nig}\) 定理、最大权匹配。缺少证明。
- 第二次编辑:\(\text{2022/02/13}\):补充了 \(\text{Hall}\) 定理、\(\text{Vizing}\) 定理及其证明。
- 第三次编辑:\(\text{2022/10/20}\):补充证明,新增稳定婚姻问题。修改了格式。
进行了一个压行。- 第四次编辑:\(\text{2022/11/02}\):增加了两个例题。
(其实是从以前博客里搬过来的题解。
二分图是啥
二分图是什么?节点由两个集合组成,且两个集合内部没有边的图。换言之,存在一种方案,将节点划分成满足以上性质的两个集合。—— OI-wiki
说的好复杂啊, 画个图理解一下。
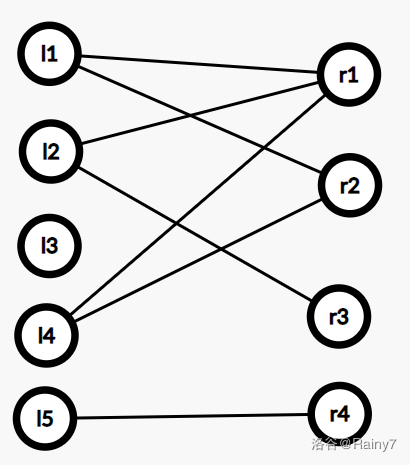
如图,在一个图中,如果能把点分为两个顶点集,使每个集合中,没有两个点有连边。
也就是说,边只会连接两个点集。
二分图判定
因为是分为两个点集,所以每个点要么属于第一个要么属于第二个。
那我们可以暴搜每个点属于什么。
显然,对于一条边所连的两个点,一定不可能属于同一个点集。
那问题可以转化一下:看成给出一个 \(n\) 个点的图,要给每个点染成黑白两色,且相邻的点颜色要不同。
那我们在搜索的时候,若点 \(u\) 属于黑色,那么与它相连的点 \(v\) 必定为白色。
这就很贪心,如果发现 \(v\) 已经被染过颜色,而且染的颜色是黑色,那么这个图就一定不是二分图了。
当然,因为相邻的两个点颜色一定不同,那意味着二分图不存在奇环。这是二分图的重要性质之一。
所以判定过程如下:
bool dfs(int x,int c)
{
color[x]=c;
for(int k=f[x];k!=0;k=p[k].nx)
{
if(color[p[k].v]==c){return 0;}
if(color[p[k].v]==0 && !dfs(p[k].v,-c)){return 0;}
}
return 1;
}
需要注意的是,给出的图不一定是连通图(除非题目有说),所以主程序的时候我们要加一个循环。
for(int i=1;i<=n;i++)
if(!color[i])if(dfs(i,1)==0){cout<<-1;return 0;}//不是二分图
完整代码如下:(我以前的码风有点丑哎(?))
#include<iostream>
#include<cstdio>
using namespace std;
struct node{
int v,nx;
}p[400001];
int f[4001],n,m,en=0;
int color[4001];
bool dfs(int x,int c)
{
color[x]=c;
for(int k=f[x];k!=0;k=p[k].nx)
{
if(color[p[k].v]==c){return 0;}
if(color[p[k].v]==0 && !dfs(p[k].v,-c)){return 0;}
}
return 1;
}
void read(int u,int v)
{
p[++en].v=v;
p[en].nx=f[u];
f[u]=en;
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1,u,v;i<=m;i++)
{
scanf("%d%d",&u,&v);
read(u,v),read(v,u);
}
for(int i=1;i<=n;i++)
if(!color[i])if(dfs(i,1)==0){cout<<-1;return 0;}
printf("1\n");
for(int i=1;i<=n;i++)
if(color[i]==1)printf("1 ");
else printf("2 ");
return 0;
}
二分图匹配
二分图匹配是什么?
匹配:在图论中,一个「匹配」是一个边的集合,其中任意两条边都没有公共顶点。
记得刚刚上面那个图嘛 (不记得就往上翻),比如这么选就是一种匹配:
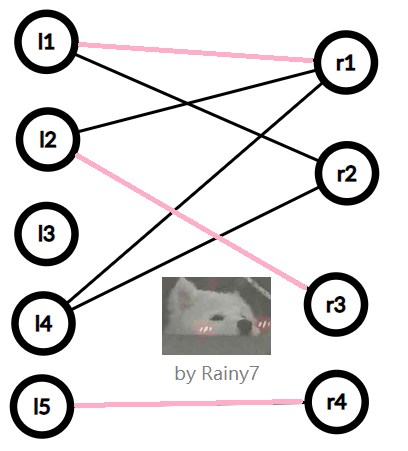
而这样就不是一个匹配:
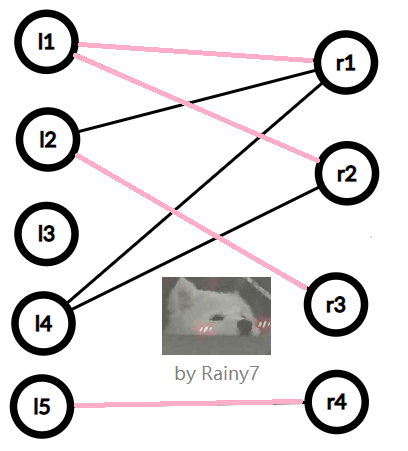
所以匹配一抓一大把。
所以要求的就成了最大匹配。
例如你谷模板 P3386 【模板】二分图最大匹配。
给定一个二分图,其左部点的个数为 \(n\) ,右部点的个数为 \(m\) ,边数为 \(e\) ,求其最大匹配的边数。
左部点从 \(1\) 至 \(n\) 编号,右部点从 \(1\) 至 \(m\) 编号。
数据范围:$1 \le n,m \le 500 , 1 \le e \le 5×10^4 , 1 \le u \le n , 1 \le v \le m $ 。
匈牙利算法
浅浅的理论知识
求二分图最大匹配的一般是用匈牙利算法 ,因为好写。
首先,要先知道一个叫增广路的东西。
若 \(P\) 是图 \(G\) 中一条连通两个未匹配顶点的路径,并且属于 \(M\) 的边和不属于 \(M\) 的边(即已匹配和待匹配的边)在 \(P\) 上交替出现,则称 \(P\) 为相对于 \(M\) 的一条增广路径(举例来说,有 \(A\)、\(B\) 集合,增广路由 \(A\) 中一个点通向B中一个点,再由 \(B\) 中这个点通向 \(A\) 中一个点……交替进行)。 ——百度百科
假设当前存在一条边 \((u,v)\),我们希望这条边加入匹配。
首先如果选的这条边满足 \((u,v)\) 都尚未匹配,那我们可以直接把这条边加入答案,这样会使匹配数加一。
但如果两个点存在一个点有匹配另一个点,不妨假设点 \(u\) 除了这条边还存在另一个匹配 \((u,v')\)。这意味着点 \(u\) 被选了两次。于是我们希望点 \(v'\) 能不选。
于是如果点 \(v'\) 所连出的边除去 \((u,v')\) 外依然存在一条边 \((v',v'')\) 没被选,那就可以扔掉 \((u,v')\) 加入 \((v',v'')\)。如果 \(v''\) 尚未有匹配点,那么就直接结束该过程。否则再对 \(v''\) 做类似 \(u\) 的判断。
这意味着我们最后找出来的路径一定是一条不是匹配的边,一条是匹配的边交替出现。以最后一点尚未匹配作为结束条件。
根据上面描述的过程,最后我们只需要反转这些边的状态,即匹配的变成非匹配边,非匹配边变成匹配边。
可以发现这就是找增广路的过程,这说明我们只要找一条增广路,然后反转上面的点即可。这意味着若存在增广路,那么答案会增加一,否则答案不会变。
那我们一直找增广路,当不存在增广路时,得到的结果就是最大匹配了。
浅浅模拟一下
以下是模拟过程,有助于理解。(顺便整活。
匈牙利算法就是一个不断找增广路的过程,那来手动模拟一下。(好多人模拟过程都是男女配对啊??)
比如这个图:
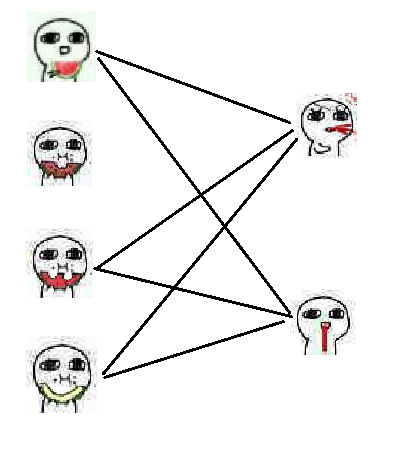
第一次匹配,我们先将第一个吃瓜人匹配到第一个吐血人:
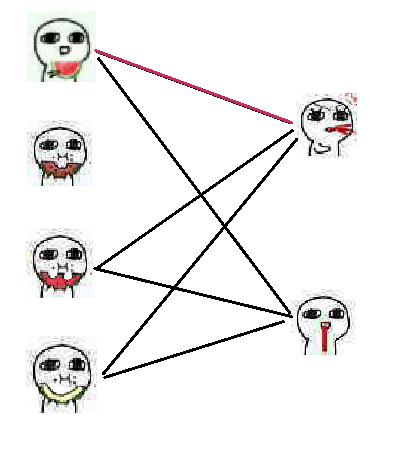
接下来,发现第二个吃瓜人是单着,那不管他了。
第三个吃瓜人,匹配到第一个吐血人,然后发现第一个吃瓜人已经和他匹配了。
那么就去协商一下,第一个吃瓜人发现还能和第二个吐血人匹配,于是第一个吐血人就给了第三个吃瓜人。如图:
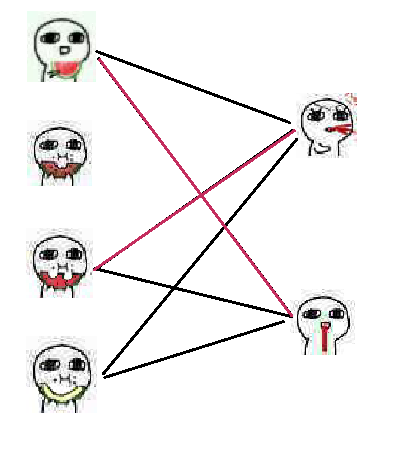
于是轮到了第四个吃瓜人,他想和第一个吐血人匹配,然后发现已经有人匹配了。
于是他和第三个吃瓜人协商, 第三个吃瓜人就选择了第二个吐血人,然后发现已经有人匹配了。
于是第三个吃瓜人去和第一个吃瓜人协商, 第一个吃瓜人选择了第一个吐血人。
结果他发现问题又绕回去了,于是第三个吃瓜人和第一个吃瓜人的协商失败,那么第三个吃瓜人和第四个吃瓜人的协商失败。
也就说,第四个人只能和第二个人一起在旁边吃瓜了。
所以最大匹配数为 \(2\) 。
这大致就是二分图匹配的过程。而协商过程,其实就是在找增广路。
也就是每个吃瓜人,都是先选择一个未匹配的边,如果对面的点(吐血人)已经被匹配了,那就顺着那个匹配的边找到那个人,那个人再选一个未匹配的边....
复杂度为 \(\mathcal{O}(nm)\) 。
匈牙利代码如下。其中 \(map_{i,j}\) 表示连边情况,\(vis\) 用来判断已经走过的点 , \(matched\) 表示改点的匹配点。
代码如下:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int N=500+5;
int n,m,e,matched[N];
int vis[N],mp[N][N];
int found(int x)
{
for(int i=1;i<=m;i++)
{
if(!mp[x][i]||vis[i])continue;
vis[i]=1;
if(!matched[i]||found(matched[i]))
{
matched[i]=x;
return 1;
}
}
return 0;
}
int match()
{
int res=0;
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(found(i))res++;
}
return res;
}
int main()
{
scanf("%d%d%d",&n,&m,&e);
for(int i=1,u,v;i<=e;i++)
{ scanf("%d%d",&u,&v);
mp[u][v]=1;
}
printf("%d\n",match());
return 0;
}
\(\text{k} \ddot{\text{o}} \text{nig}\) 定理
内容
这个名字真难打。
点覆盖,在图论中点覆盖的概念定义如下:对于图G=(V,E)中的一个点覆盖是一个集合S⊆V使得每一条边至少有一个端点在S中。 -----百度百科
举个例子,这个图的,选择 \(2,4,5\)就是一种点覆盖。这种情况的点覆盖数为 \(3\) 。
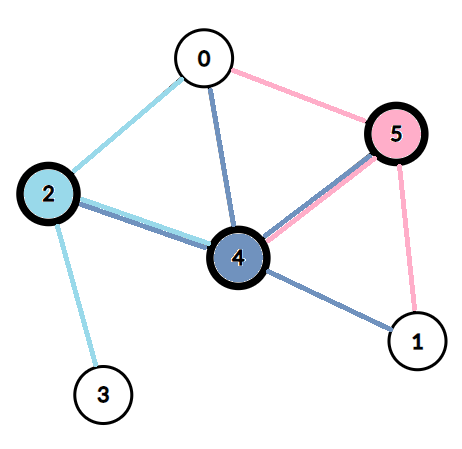
很明显,每个图的最大点覆盖就是点数。也就是说,不存在没有点覆盖的图。
所以一般都是求最小点覆盖。
那现在来探讨一下二分图的最小点覆盖(不能遗忘标题)。
然后这就有一个定理:二分图的最小点覆盖=二分图的最大匹配。
证明
假设当前存在一条边 \((u,v)\) 尚未被覆盖。
如果两个点存在一个点(不妨设为 \(u\))他满足不存在一条边 \((u,v')(v' \not= v)\) 且 \(v'\) 在点覆盖点集内,那么自然可以选 \(u\)。
因为我们希望点覆盖的点尽量小,所以尝试选 \(u\) 去掉 \(v'\),那意味着与 \(v'\) 相邻的 \(u' (u' \not= u)\),也必须选。这是一个找增广路的过程。
那这意味着图中不存在增广路时,此时选的点集一定能覆盖整张图。
接着考虑一张二分图没有增广路的情形。不妨设在匹配的点为红色,不在匹配内的点为蓝色。那么边只有连接着两个红点,或者连接着一红一蓝的边。
对于一条匹配边 \((u,v)\),如果 \(u\) 连接的点中有蓝边,那么 \(v\) 边一定不存在蓝边,否则此时会存在一条增广路。
如果匹配边 \((u,v)\) 存在一个点会连接蓝点(不妨为 \(u\)),那此时,我们选择点 \(u\) 到点覆盖点集中。
那么此时剩余的匹配边一定满足 \(u,v\) 都只连接红点,所以不妨设左右部图各有 \(m\) 个点,我们只需要将其中一部的红点全部选上即可。
根据此方法,最后得出来的点集一定满足条件。
如果此时少选一个点,不妨看成直接去掉这个点的匹配,那么一定会存在增广路,那么就会存在边尚未覆盖。
于是二分图的最小点覆盖=二分图的最大匹配,得证。
二分图的最小边覆盖
内容
有最小点覆盖,就有一个东西叫最小边覆盖。
边覆盖是一类覆盖,指一类边子集。具体地说,图的一个边子集,使该图上每一节点都与这个边子集中的一条边关联。 —— 百度百科
如图,边覆盖为 \(3\) 。
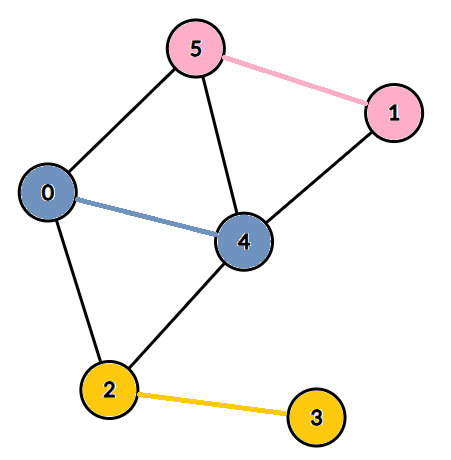
那么是否每个图都有边覆盖呢?
显然,如果一个图含有一个孤立点,那么这个图不可能有边覆盖。
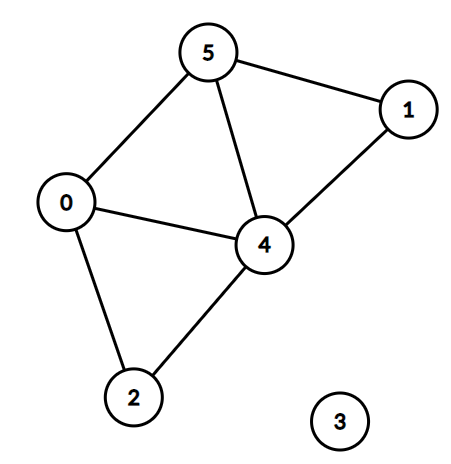
那有一个定理:二分图中最小边覆盖=顶点数-二分图最大匹配。
也就是说可以简单替换一下:二分图中最小边覆盖+最小顶点覆盖=顶点数。
证明
首先对于一个不存在孤立点的二分图,为了边覆盖数量最小,肯定会优先选择最大匹配的边,因为这个边可以一个覆盖 \(2\) 个点而且相互之间不重复。
假设总边数是 \(n\) ,最大匹配数是 \(m\) ,则剩下的点数为 \((n-2m)\) 。
剩下的边已经不存在一个边能覆盖 \(2\) 个没有覆盖的点,所以对于剩下的点需要 \((n-2m)\) 条边来覆盖。
所以最小边覆盖为 \((n-2m)+m=n-m\) ,即二分图中最小边覆盖为顶点数减去二分图最大匹配。
独立集
内容
独立集是指图 G 中两两互不相邻的顶点构成的集合。 ---百度百科
举个例子,如下图,独立集个数为 \(3\) 。
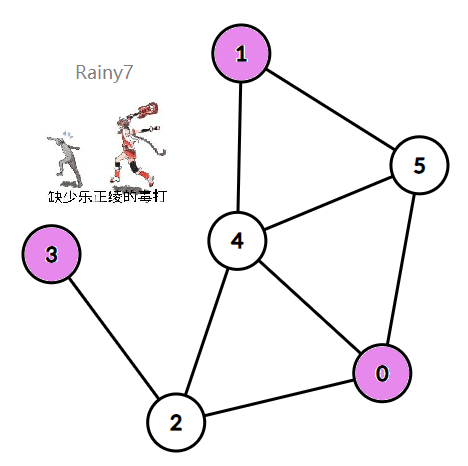
最小独立集没啥好求的,所以要解决的问题就是二分图的最大独立集。
这又双叒有一个公式:二分图的最大独立集 = 总点数 - 最大匹配数。
证明
注意到如果我们将非独立集中的点及其所连的边删掉,那么剩下的点一定不存在连边。
这就提示我们,非独立集一定是一个点覆盖。也就是说明独立集 = 总点数 - 点覆盖数。
于是最大独立集 = 总点数 - 最小点覆盖 = 总点数 - 最大匹配数。得证。
一般图最小路径覆盖
内容
此题更偏向于例题。那么我们就用二分图过了这个网络流24题。
给定有向图 \(G=(V,E)\) 。设 \(P\) 是 \(G\) 的一个简单路(顶点不相交)的集合。如果 \(V\) 中每个定点恰好在P的一条路上,则称 \(P\) 是 \(G\) 的一个路径覆盖。 \(P\) 中路径可以从 V 的任何一个定点开始,长度也是任意的,特别地,可以为 \(0\) 。\(G\) 的最小路径覆盖是 \(G\) 所含路径条数最少的路径覆盖。设计一个有效算法求一个 GAP (有向无环图) \(G\) 的最小路径覆盖。
如下图,最小路径数为 \(3\) ,分别为:\(1 \rightarrow 4 \rightarrow 7 \rightarrow 10 \rightarrow 11,2 \rightarrow 5 \rightarrow 8,3\rightarrow 6 \rightarrow 9\)。

考虑建一个二分图。
假设图两边的点数都为 \(n\) ,左边编号表示为 \(i\) ,右边编号表示为 \(i'\) 。
每次读入一条边 \((u,v)\) 时,在二分图连边 \((u,v')\) 。
建完图跑二分图最大匹配,结果为:最小路径覆盖=顶点数-最大匹配数。
证明
题目中已经说明,一个单独的点也为路径,如果 \(u_1,u_2,u_3,...u_n\) 为一条路径,那 \(u_1\) 到 \(u_n\) 之间不会有其他的有向边。
如果此时最大匹配数为 \(0\) ,则二分图中无边,显然最小路径覆盖=顶点数-最大匹配数=顶点数。
若此时增加一条匹配边 \((x,y')\) ,则在有向图中,\(x,y'\)在同一条路径上,最小路径覆盖减一。
若继续增加匹配边,那么最小路径继续覆盖减一,所以公式得证。
那么路径要怎么求呢。
直接沿着增广路跑循环就可以了。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int Maxn=300+5,Maxm=6000+5;
int n,m,ans,matched[Maxn];
bool vis[Maxn],mp[Maxn][Maxn];
bool found(int x)
{
for(int i=n+1;i<=2*n;i++)
{ if(!mp[x][i]||vis[i])continue;
vis[i]=1;
if(!matched[i]||found(matched[i]))
{ matched[i]=x;
matched[x]=i;
return 1;
}
}
return 0;
}
int match()
{
int cnt=0;
for(int i=1;i<=n;i++)
{ memset(vis,0,sizeof(vis));
if(found(i))cnt++;
}
return cnt;
}
void prt(int x)
{
x+=n;
do
printf("%d ",x=x-n);
while(vis[x]=1,x=matched[x]);
printf("\n");
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
mp[u][v+n]=1;
}
ans=n-match();
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
if(!vis[i])prt(i);
printf("%d\n",ans);
return 0;
}
KM 算法
二分图最大权匹配。 你说的对但是我选择费用流。
\(\text{upt 2020/08/05}\):有模板了 P6577 【模板】二分图最大权完美匹配。
洛谷似乎没有模板,那就用这题P3967 [TJOI2014]匹配。单看第一问就是个模板(确信)。
给定一个二分图,两边的点数都为 \(n\) ,给出若干条边,每条边有一个权值,求最大的完美匹配的值。
KM 针对的是带权的完美匹配,就是说二分图两边的数量必须相等,即最大匹配数为 \(n\) 。
其实 KM 的复杂度和边没太多关系,所以如果两点没有连边的话,可以假设这两点的边的权值为 \(0\) 。
首先,每个点有一个顶标,就是有一个值。
假设点 \(u\) 的顶标为 \(l(u)\) 。
对于任意一条边 \((u,v)\) ,必须满足 \(l(u)+l(v) \ge w(u,v)\) ,其中\(w\)表示边权。
当一条边满足 \(l(u)+l(v)=w(u,v)\) 时,就可以把这条边加入二分图中。
如果该图可以跑出完美匹配,那么此时的完美匹配的边权值和的即为结果。
似乎很简单的样子, 那么怎么确定顶标的值呢。
因为不能直接确定,那算法流程大概是这样子:确认顶标的值->跑匹配->如果匹配数为 \(n\) ,结束;否则->修改顶标->跑匹配.....
那初始的时候顶标该如何确定呢?
假设二分图左边的顶标为 \(ex(i)\) ,右边的顶标为 \(ey(i)\) 。
因为要满足 \(ex(x)+ey(y) \ge w(x,y)\),那我们不妨直接设 \(ex(i)\) 全部为 \(0\),\(ey(i)\) 为所连边的最大值。
调整顶标过程中,其实目的就是要不断的加入新的边,也就是使更多的边满足 \(ex(i)+ey(j)=w(i,j)\) 。
那么接下来找一条边 \((i,j)\) ,使其满足 \(i\) 不在二分图最大匹配中,而 \(j\) 在二分图最大匹配中。
我们希望这条边加入二分图匹配,就要使这条边满足条件,即顶标和要减少 \(d=ex(i)+ey(j)-w(i,j)\) 。
因为此时点 \(j\) 在二分图最大匹配中,如果改变顶标肯定会影响其他边,所以干脆草率一点,对于在二分图最大匹配中的任意点 \(i\) ,将 \(ex(i)+d\) 或 \(ey(i)-d\) 。
为了防止修改完导致部分顶标不满足 \(ex(x)+ey(y) \ge w(x,y)\) ,我们每次找的 \(d\) 要尽量小。
ok,解决了,算一下复杂度。
每次找边复杂度为 \(O(n^2)\) ,二分图最大匹配的复杂度为 \(O(n^2)\) ,也就是说总复杂度为 \(O(n^4)\) 。
有一说一,这是真的慢。考虑优化,至少优化到 \(O(n^3)\) 啊!!
每次找一遍 \(d\) 太慢了,所以我们开个数组:\(slack[j]= \min (ex(i)+ey(j)-w(i,j))\)。
每次查询的时候就降了一维,\(slack\) 修改只要在跑增广路的时候修改就好了。
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int Maxn=303;
const int inf=1e9;
int n,map[Maxn][Maxn],matched[Maxn];
int slack[Maxn],ex[Maxn],ey[Maxn];//ex,ey顶标
bool visx[Maxn],visy[Maxn];
bool match(int x)
{
visy[x]=1;
for(int i=1;i<=n;i++)
{
if(visx[i])continue;
int gap=ex[i]+ey[x]-map[x][i];
if(gap==0)
{
visx[i]=1;
if(!matched[i]||match(matched[i]))
{
matched[i]=x;
return 1;
}
}
else slack[i]=min(slack[i],gap);
}
return 0;
}
int KM()
{
memset(matched,0,sizeof(matched));
memset(ex,0,sizeof(ex));
for(int i=1;i<=n;i++)
{
ey[i]=map[i][1];
for(int j=2;j<=n;j++)
ey[i]=max(ey[i],map[i][j]);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)slack[j]=inf;
while(1)
{
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(match(i))break;
int d=inf;
for(int j=1;j<=n;j++)
if(!visx[j])d=min(d,slack[j]);
for(int j=1;j<=n;j++)
{
if(visy[j])ey[j]-=d;
if(visx[j])ex[j]+=d;
else slack[j]-=d;
}
}
}
int res=0;
for(int i=1;i<=n;i++)
res+=map[matched[i]][i];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&map[i][j]);
printf("%d\n",KM());
return 0;
}
然后就会发现,哎不对啊这个 \(O(n^3)\) 是假的啊。
只要数据够duliu, 匹配的部分跑到 \(O(n^2)\) ,那么复杂度依然没有降到 \(O(n^3)\) 。
接下来就会发现,因为我们每次只修改一条边,也就是说dfs跑匹配的时候,有一部分和之前是一样的。
所以我们把dfs改成bfs,就可以实现真正的 \(O(n^3)\) 。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int Maxn=303;
const int inf=1e9;
int n,map[Maxn][Maxn],matched[Maxn];
int slack[Maxn],pre[Maxn],ex[Maxn],ey[Maxn];//ex,ey顶标
bool visx[Maxn],visy[Maxn];
void match(int u)
{
int x,y=0,yy=0,delta;
memset(pre,0,sizeof(pre));
for(int i=1;i<=n;i++)slack[i]=inf;
matched[y]=u;
while(1)
{
x=matched[y];delta=inf;visy[y]=1;
for(int i=1;i<=n;i++)
{
if(visy[i])continue;
if(slack[i]>ex[x]+ey[i]-map[x][i])
{
slack[i]=ex[x]+ey[i]-map[x][i];
pre[i]=y;
}
if(slack[i]<delta){delta=slack[i];yy=i;}
}
for(int i=0;i<=n;i++)
{
if(visy[i])ex[matched[i]]-=delta,ey[i]+=delta;
else slack[i]-=delta;
}
y=yy;
if(matched[y]==-1)break;
}
while(y){matched[y]=matched[pre[y]];y=pre[y];}
}
int KM()
{
memset(matched,-1,sizeof(matched));
memset(ex,0,sizeof(ex));
memset(ey,0,sizeof(ey));
for(int i=1;i<=n;i++)
{
memset(visy,0,sizeof(visy));
match(i);
}
int res=0;
for(int i=1;i<=n;i++)
if(matched[i]!=-1)res+=map[matched[i]][i];
return res;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&map[i][j]);
printf("%d\n",KM());
return 0;
}
\(\text{Hall}\) 定理
内容
设 \(N(S)\) 表示与 \(S\) 中的点相连的点集。
如果一个二分图 \(G(V_1,V_2,E)\) ,其中 \((|V_1| \le |V_2|)\) ,若满足对于 \(V_1\) 任意点集 \(Q\) 有 \(|Q| \le |N(Q)|\) ,则存在完美匹配。反之亦然。
先证明必要性。若存在完美匹配 \(M\) ,而 \(M\) 中将 \(Q\) 中的点都有一个匹配点,也就是说和 \(N(Q)\) 中都有一个匹配点,那么显然 \(|Q| \le |N(Q)|\) 。
再证明充要性。
考虑用网络流证明,我们把这个图定向,\(V_1 \to V_2\) ,然后加一个源点汇点 \(s,t\) 。设 \(P_u(x,y)\) 为 \(G\) 中 \(x\) 到 \(y\) 的点不交的路径集合。设 \(f_u(x,y)=\max ( | P_u(x,y) | )\) ,设 \(g_u(x,y)\) 表示让 \(x,y\) 不连通,最少删除的点数。由 \(\text{Menger}\) 定理的点形式即 \(f_u(x,y)=g_u(x,y)\) 。
于是设 \(T\) 为删除点使 \(s,t\) 的最小点集。设 \(T_1=T \cap V_1,T_2=T \cap V_2\) 。
所以设最大流为 \(flow=|M|=f_u(s,t)=g_u(s,t)=|T|\) 。则有 \(N(V_1 \setminus T_1) \subset T_2\) 。
于是又有 \(|M|=|T|=|T_1|+|T_2| \ge |T_1| + |N(V_1 \setminus T_1)| \ge |T_1|+|V_1 \setminus T_1|=|V_1|\) 。
所以 \(|M| \ge |V_1|\) 但又因为显然 \(|M| \le |V_1|\) 。所以 \(|M|=|V_1|\) 。
例题
有 \(n\) 个人玩 \(m\) 台游戏机,每台游戏机一秒内只能一人玩,每人一秒内只能玩一台。
每台游戏机有个价格,在规定总价格内可以把一部分游戏机复制一次,每台只能复制一次。
给每个人对在每台游戏机上的需求时间,求一种方案使得所有玩游戏结束的时间尽量早。
其中 \(n \le 120,m \le 60\) 。
我们先考虑没有买机器这一操作。
不妨假设每个孩子要玩每个机器,把不是题目给定的都设为 \(t_{i,j}=0\) 。不妨设 \(r_i=\sum\limits_{j=1}^m t_{i,j},c_j=\sum\limits_{i=1}^nt_{i,j}\) 。
于是可以发现答案的下限是 \(T=\max(\max\limits_{i=1}^n\{ r_i \},\max\limits_{i=1}^m\{ c_i \})\) 。接下来我们尝试证明一定存在一个时间安排使得最后的时间为 \(T\) 。
考虑建一张二分图,使得二分图两边都有 \(n+m\) 个点。然后把每个人和每个机器连起来表示时间。
当然因为并没有 \(n+m\) 个点。所以我们设 \(n+1 \sim n+m\) 的孩子表示虚假的孩子。然后把 \(u_{n+i}\) 和 \(i\) 机器连边。
同理,\(m+1 \sim n+m\) 的机器表示虚假的机器。把 \(v_{m+i}\) 和 \(i\) 小孩连边。
于是会有四种边。(1) 真孩子和真机器 (2) 假孩子和真机器 (3) 真孩子和假机器 (4) 假孩子和假机器
然后我们尝试保证每个点的连出去的边边权和为 \(T\) 。
第一种。对于 \((u_i,v_j)\) 。如果 \(t_{i,j}>0\) 就设其为边权。
第二种。这意味着这个机器会剩下一些时间。于是他会有一段 \(T-c_j\) 的时间(权值和)连向假孩子。
第三种。类似的,孩子会剩下一些时间,于是会有 \(T-r_i\) 的时间(权值和)连向假机器。
第四种。此时可以发现对于真的点边权和都是 \(T\) ,而假的不是。所以我们通过假的和假的连边使得假点度数也为 \(T\) 。
于是根据 Hall 定理,我们发现对于任何一种二分图都有完美匹配。
如果有钱的话,对于一个 \(j\) 满足 \(c_j=T\) 时,考虑把 \(c_j\) ,把机器拆开使 \(T\) 变小,一份拆成 \(\left\lfloor \dfrac{T}{2} \right\rfloor\) ,另一份拆成 \(\left\lceil \dfrac{T}{2} \right\rceil\)。能用就用,直到不行。
然后根据这个答案再来构造。构造过程类似下面的最小边染色。
\(\text{Vizing}\) 定理
内容
对于一张二分图,定义最大点的度数为 \(\delta\) ,最少需要的颜色为 \(f\) ,则有 \(f(G)=\delta(G)\) 。
首先肯定有 \(f(G) \ge \delta(G)\) 考虑数学归纳法,设有 \(m\) 条边。
当 \(m=0\) 时,有 \(d=f=0\) 。
假设当 \(m=k\) 时成立,则当 \(m=k+1\) 时,不妨设当前的图为 \(G=(V,E)\) 。设一条边 \(e=(u,v) \in E\) 。设一个不含 \(e\) 的图为 \(G'\) 。
于是有 $ f(G') = \delta(G') \le \delta(G)$ 。
染色时,一定存在一个颜色不在 \(u\) 所连出去边集的颜色中,\(v\) 也一样。
如果此时同时存在一个没有出现的颜色,那么对 \((u,v)\) 染上这个颜色即可。
如果没有这种颜色,我们不妨考虑最差情况,也就是说 \(u\) 只有一个颜色 \(lx\) 没出现,\(v\) 只有 \(ly\) 。
反之,\(u\) 连的边有 \(ly\) ,\(v\) 连的边有 \(lx\) 。
我们设图 \(G_s'\) 表示所有为 \(lx\) 或 \(ly\) 的边的子图。此时可发现,如果 \(u,v\) 不联通,就一定存在一个染色方法。将一个连通块反过来染色即可。
不妨假设 \(u,v\) 是连通的,因为 \(u,v\) 分别在左右部,所以路径长度一定为奇数,并且是两个颜色交错出现的。
那么一个颜色,假设是 \(lx\) ,第一个出现,那么也会以这个颜色结束。这么说明 \(lx\) 同时出现在 \(u,v\) 中。与假设矛盾。
所以 \(u,v\) 是不联通的。所以得证。所以我们只要将一个连通块的 \(lx\) 和 \(ly\) 反过来就好了。
除了对于二分图,对于一个简单图也有结论。
对于一个没有自环的简单图,有 $\delta(G) \le f(G) \le \delta(G)+1 $ 。
但因为标题是二分图所以先不写证明。
例题
给定 \(n+m\) 个点 \(k\) 条边的二分图,左边 \(n\) 个点,右面 \(m\) 个点。现在要把每条边标号,标号为 \(1 \sim t\)。
求出最小的对于每个点与之相邻的边中最多的标号与最少标号的数量差的平均值。
输出这个和并且输出一组构造方案。
其中 \(n,m,t \le 200, k \le 5000\) 。
首先答案的下限是所有度数不为 \(t\) 的倍数的点。原因显然,如果一个点的度数为 \(t\) 的倍数,那么标号可以平均分配。而对于不是 \(t\) 倍数的点,他们的不均衡值( \(\max-\min\) )至少为 \(1\) 。
于是考虑一些边然后使每个点的度数都为 \(t\) 的倍数,然后把这些点分成 \(\dfrac{d_i}{t}\) 个块,每一块中每个编号恰好出现一次。
考虑剩下边的情况。于是为了使答案达到下限,即一个点的贡献只为 \(1\) ,意味着这变成了最小边染色问题,由 Vizing 定理得,此时最小的颜色数就是最大点度数。
对于剩下的边,考虑一个 \((u,v)\) 加入的情况,设此时 \(u,v\) 最小没被染的颜色是 \(t_1,t_2\) 。如果他们相等,可以直接连边;否则直接找增广路,因为 \(\text{Vizing}\) 定理所以一定存在,复杂度是 \(\mathcal{O}(m^2)\) 。
稳定婚姻问题
内容
有 \(n\) 个男生, \(n\) 个女生,每人对所有异性有一个排名要求一个完美匹配,使得不存在两对情侣中两个异性看对方都比自己情侣更好。
其中 \(n \le 2000\) 。
题目来源竟然是现实生活!!!(问题来自于一场“3分钟相亲”活动——百度
应该算是二分图的一种问题吧。
从每一个男生考虑。每次找一个仍孤寡的男生。找到一个愿意和他一起的最好女生。如果那个女生有配偶就扔掉她的配偶。然后把重新孤寡的男生放进孤寡男生队列里。
复杂度 \(\mathcal{O}(n^2)\) 。
例题
这是一道交互题。
Alice 和 Bob 又在玩游戏。
有一张二分图,左右各 \(n\) 个点,左右的点之间两两有边,每条边有边权,保证边权两两不同。将左边的点标号为 \(1 \sim n\),右边的点为 \(n+1 \sim 2n\)。
游戏的开始,甲需要选择增加或者减少,乙则会自动选择另一项,之后甲需要选定一个点,将棋子放在上面。接着从乙开始,轮流移动棋子移动到一个之前没有移动到过的相邻点上,要求移动时要满足之前的选项,即如果甲选择增加,那么本次移动的边权必须大于上次移动的边权,减小通理,乙也是如此(第一次移动除外),第一个无法移动的人输了。
由 Alice 决定做甲还是乙,帮助 Alice 与 Bob(交互库)对决,赢下这场游戏。
类似二分图博弈。只要甲走时候乙能有一个匹配边就是必胜。于是我们考虑一个二分图最大权完美匹配。
首先注意到递增递减本质不变,所以我们只考虑选先手增加的情况。
考虑一组情况左边点为 \(x,y\) 右边的点为 \(w,z\) 。有匹配 \((x,w),(y,z)\) 。
于是先手从 \(x\) 移到 \(y\) 的时候,有 \((x,y)>(x,w),(x,y)>(y,z)\) 。
于是我们要构造出一个完美匹配,使得不存在匹配边满足 \((x,w)<(x,y)<(y,z)\) 。
这是一个稳定婚姻问题。对于左边,按照权值由大到小来设排行;右边相反。
由于稳定婚姻问题一定有解,于是乙必胜。


