「后缀排序SA」学习笔记
-
前言
upd 2021/08/28:感谢@Fее_cle6418指出的一个错误。
求赞QWQ
所以..到底是啥神仙脑洞这么大想到这种
神奇毒瘤的东西?
-
求什么
就比如洛谷的 P3809 【模板】后缀排序 (SA)
读入一个长度为 \(n\) 的由大小写英文字母或数字组成的字符串,请把这个字符串的所有非空后缀按字典序从小到大排序,然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 \(1\) 到 \(n\) 。
其中 \(n \le 10^6\) 。
直接排序的复杂度为 \(O(n^2 \log n)\)
所以SA肯定比这快嘛..为 \(O(n \log n)\)
然后补充一下,这题不用求LCP(最长公共前缀),但是好像这东西很有用..(
-
后缀排序思想
用了基数排序的思想呐。
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用
----百度百科其实上面那个定义不重要,后缀排序就是利用了基数排序的思想。按照字典序排列,若一一比较,肯定先从第一位开始比。所以我们可以按照每个后缀的第一个字符排个序,这个操作相当于把这个字符串的每个字符排个序。
除非正好每个字符不一样,否则肯定有部分的字符是排名是一样的,按照排序,接下来要比较这些排名一样的字符的第二位!
然后复杂度就上去了。其实,第二位我们已经比较过了!
因为要排序的是后缀,所以第 \(i\) 个后缀的第二个字符就是第 \(i+1\) 个字符,也就是已经排序好了,而第一位是第一关键字,第二位是第二关键字。
那么就可以得到第二位的排序。
以此类推,可以利用倍增的思想,再利用已知去得出第四位的排序。
不难得出,当所有后缀的排名都两两不同时,就完成了本题。
直接理解确实十分硬核,所以下面结合图再做说明。
每个后缀的编号如题目,为第一个字母所在的位置。
\(s\) 表示这个字符串。
\(sa_i\) 表示排名为 \(i\) 的后缀编号是什么。
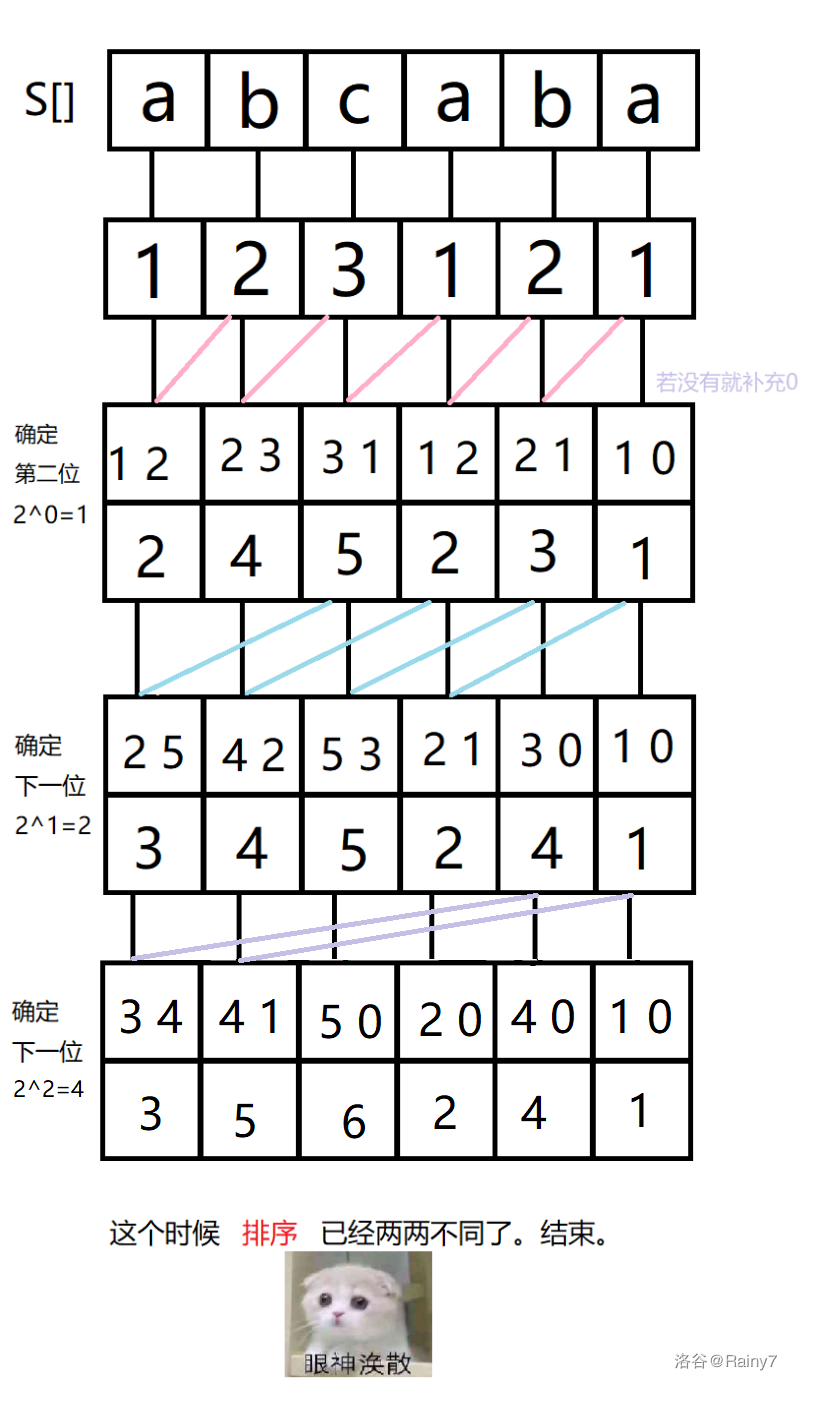
那么接下来更毒瘤的来了
-
后缀排序代码理解
打算一块一块讲,算上输出我总共写了12个for。
首先,我们要先根据第一位排序,确定最初的 \(sa\) 。
我们用 \(x_i\) 表示第一关键字。
for(int i=1;i<=n;i++){x[i]=s[i];++c[x[i]];} for(int i=2;i<=m;i++)c[i]+=c[i-1]; for(int i=n;i>=1;i--)sa[c[x[i]]--]=i;先直接把 \(s_i\) 给上 \(x_i\) ,而 \(c\) 数组是桶,这里用到的就是桶排序的思想,来统计每种字符有多少种。
为了方便标号,就先做一个前缀和。这样字典序越大,所对应的的 \(c\) 越大。
接下来就是排序确定最初 \(sa\) 了。再次强调: \(sa_i\) 表示排名为i的后缀编号是什么。
至于为什么 \(c_{x_i}\) 要减一,是为了当出现 \(c_{x_i}>1\) ,即有重复时,保证排序不一样。

下一块,就是要一步一步确定第二位,第四位..
也就是利用倍增的思想:
for(int k=1;k<=n;k=k<<1)然后就在这循环里瞎搞就好了。首先,定义 \(y_i\) 表示排名为第 \(i\) 的第二关键字 ,也就是确定 \(x\) 的排列的东西。
然后根据上次排序的 \(sa\) 来确定 \(y\) 。
int num=0; for (int i=n-k+1;i<=n;++i) y[++num]=i; for(int i=1;i<=n;i++) if(sa[i]>k)y[++num]=sa[i]-k;\(num\) 只是一个指针而已。
首先后 \(k\) 位,也就是第 \(n-k+1\) 位到第 \(n\) 位,他们其实已经排序完了,因为他们后面的第 \(k\) 位不存在。那么先直接存在 \(y\) 中。
若第 \(i\) 位可作其他位置的第二关键字,即 \(sa_i>k\) 时,要把他放在对应的第一关键字( \(x_{sa_i-k}\) )中。

确定完第一关键字和第二关键字,就可以更新 \(sa\) 了。而且更新方法和开头很像。
for(int i=1;i<=m;i++)c[i]=0; for(int i=1;i<=n;i++)c[x[i]]++; for(int i=2;i<=m;i++)c[i]+=c[i-1]; for(int i=n;i>=1;i--){sa[c[x[y[i]]]--]=y[i];y[i]=0;}首先清空,然后用桶统计,然后前缀和。
唯一改的就是把
sa[c[x[i]]--]=i;改成sa[c[x[y[i]]]--]=y[i];原因也很简单,就是因为开头 \(x\) 排序就是 \(1\) 到 \(n\) ,而这边排序变成了 \(y_1\) 到 \(y_n\) 。

接下来就是要更新 \(x\) 了,然后很明显,要用到未更新的 \(x\) 和 \(sa\) 。
然后又懒得开新变量存,所以先用暂时没用的 \(y\) 来存此时的 \(x\) 。
swap(x,y);然后更新。
num=1;x[sa[1]]=1; for(int i=2;i<=n;i++) { if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])x[sa[i]]=num; else x[sa[i]]=++num; } if(num==n)break; m=num;//m是指不同字母的数量此时 \(i\) 代表的是排名,所以编号都要用 \(sa_i\) 代替。
然后当两个字符一样的时候,\(x\) 是一样的,也就是第一个if判断。
否则的话排名更新,因为是按照排名枚举的,所以直接 \(num+1\) 。
当 \(x_i\) 各不相同时,即 \(num=n\) 时,这个排序也就做完了。
然后这部分就做完了..
-
后缀排序完整代码(即P3809 【模板】后缀排序 (SA)完整代码)
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; const int Maxn=1e6+5; char s[Maxn]; int n,m,x[Maxn],y[Maxn],c[Maxn],sa[Maxn]; int height[Maxn],rk[Maxn]; void SA() { for(int i=1;i<=n;i++){x[i]=s[i];++c[x[i]];} for(int i=2;i<=m;i++)c[i]+=c[i-1]; for(int i=n;i>=1;i--)sa[c[x[i]]--]=i; for(int k=1;k<=n;k=k<<1) { int num=0; for (int i=n-k+1;i<=n;++i) y[++num]=i; for(int i=1;i<=n;i++) if(sa[i]>k)y[++num]=sa[i]-k; for(int i=1;i<=m;i++)c[i]=0; for(int i=1;i<=n;i++)c[x[i]]++; for(int i=2;i<=m;i++)c[i]+=c[i-1]; for(int i=n;i>=1;i--){sa[c[x[y[i]]]--]=y[i];y[i]=0;} swap(x,y); num=1;x[sa[1]]=1; for(int i=2;i<=n;i++) { if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])x[sa[i]]=num; else x[sa[i]]=++num; } if(num==n)break; m=num; } for(int i=1;i<=n;i++) printf("%d ",sa[i]); printf("\n"); } int main() { scanf("%s",s+1); n=strlen(s+1); m=122; SA(); //LCP(); return 0; }
-
LCP
这个
据说好用的东西就顺带讲了吧。LCP:最长公共前缀。然后就是求,要用到后缀排序。
定义 \(LCP(i,j)\) 表示第 \(sa_i\) 个和第 \(sa_j\) 个的两个后缀的最长公共前缀。
然后就是一堆定理:
- \(LCP(i,j)=LCP(j,i)\)
- \(LCP(i,i)=len(sa_i)=n-sa_i+1\)
- LCP Lemma \(LCP(i,j)=\min(LCP(i,k),LCP(k,j))(1 \le i \le k \le j \le n)\)
- LCP Theorem \(LCP(i,j)=\min(LCP(k,k-1))(1<i \le k \le j \le n)\)
那么如何证明呢?
首先定理 \(1\) 和定理 \(2\) 是显然的。
然后LCP Lemma和LCP Theorem开始
抄别人文章。-
LCP Lemma
设 \(p=\min(LCP(i,k),LCP(k,j))\) ,则 \(LCP(i,k) \ge p\) , \(LCP(k,j) \ge p\)。
设第 \(sa_i\) 后缀为 \(u\) ,第 \(sa_j\) 后缀为 \(v\) ,第 \(sa_k\) 后缀为 \(w\) 。
所以 \(u\) 和 \(w\) 的前 \(p\) 个字符相等,\(v\) 和 \(w\) 的前 \(p\) 个字符相等。
所以 \(u\) 和 \(v\) 的前 \(p\) 个字符相等。
设 \(LCP(i,j)=q\),且 \(q > p\) 。
则 \(q \ge p+1\) ,且 \(u_{p+1} = v_{p+1}\)
因为 \(p=\min(LCP(i,k),LCP(k,j))\) ,所以 $u_{p+1} \ne w_{p+1} $ 或者 \(v_{p+1} \ne w_{p+1}\)
所以 \(u_{p+1} \ne v_{p+1}\) 与前面矛盾。
所以 \(LCP(i,j) \le p\)
综上所述, \(LCP(i,j)=p=\min(LCP(i,k),LCP(k,j))(1 \le i \le k \le j \le n)\)
-
LCP Theorem
把 \(i\) ~\(j\) 拆成 \(i\)~\(i+1\) 和 \(i+1\)~\(j\)
那么根据LCP Lemma,则 \(LCP(i,j)=\min(LCP(i,i+1),LCP(i+1,j))\)
然后我们依然可以把 \(i+1\) 到 \(j\) 继续拆,明显正确。
好的那么接下来的问题就是怎么求了。
我们设 \(rk_i\) 表示编号为 \(i\) 的后缀的排名。
请注意和前面的 \(sa_i\) 区分,他们是这个关系:\(sa_{rk_i}=i\)。
设 \(height(i)=LCP(i,i-1)(1<i\le n)\) ,\(height(1)=0\) 。
因为 \(LCP(i,j)=\min(LCP(k,k-1))(1<i \le k \le j \le n)\)
所以 \(LCP(i,j)=\min(height(k))(i < k \le j)\)
设 \(h_i=height(rk_i)\)
因为 \(sa_{rk_i}=i\)
所以 \(height(i)=h_{sa_i}\)
然后这里其实是有一个定理的 \(h_i \ge h_{i-1}-1\) 。
但是我并不会证明。然后就可以用这条定理来求 \(height\) ,然后再求LCP。
void LCP() { int k=0; //用k代表h[i] for(int i=1;i<=n;i++)rk[sa[i]]=i; //初始化rk[i] for(int i=1;i<=n;i++)//这里其实是枚举rk[i] { if(rk[i]==1)continue; //height[1]=0 if(k)k--; //h[i]>=h[i-1]-1,更新k然后一位位枚举 int j=sa[rk[i]-1];//前一位字符串 while(i+k<=n&&j+k<=n&&s[i+k]==s[j+k])k++;//一位位枚举 height[rk[i]]=k;//h[i]=height[rk[i]] } for(int i=1;i<=n;i++) printf("%d ",height[i]); printf("\n"); }然后就可以求 LCP 了。
根据 \(LCP(i,j)=\min(height(k))(i < k \le j)\)
int ans=inf;//求LCP(x,y) for(int i=x+1;i<=y;i++) ans=min(ans,height(i)); printf("%d\n",ans);


