「树链剖分」学习笔记

前言

未经允许，请勿转载。

写这道题写了好久..当然都是在调..

最后发现线段树把 build(1,n,1) 写成 build(1,1,n)

..然后..然后就想写个学习笔记吧。

~~当然还有一部分原因是我博客好久没更新了~~

线段树

所以不会线段树的这里走。

关于我的线段树：

build(int l,int r,int k) 建树，到[l,r]，下标k
void pushdown(int l,int r,int k) 懒标记下传
int query(int l,int r,int x,int y,int k) 查询[x,y]的和，递归到[l,r]，下标为k
void add(int l,int r,int x,int y,int z,int k) 把[x,y]中每个数加上z，递归到[l,r]，下标k

求什么

顾名思义，把树当成链~~进行一些非人类~~操作，比如查询和修改。

然后在序列中，快速区间加和区间查询，这就要用到线段树。

例如在洛谷模板3384中，要支持4种操作：

1.将树从\(x\)到\(y\)结点最短路径上所有节点的值都加上\(z\)

2.求树从\(x\)到\(y\)结点最短路径上所有节点的值之和

3.将以\(x\)为根节点的子树内所有节点值都加上\(z\)

4.求以\(x\)为根节点的子树内所有节点值之和
概念
1. 重(zhòng)儿子：对于除了叶节点以外的点，在它的儿子中子节点数最多的就是它的重儿子。
  
  例如：(重儿子用\(son[]\)表示)
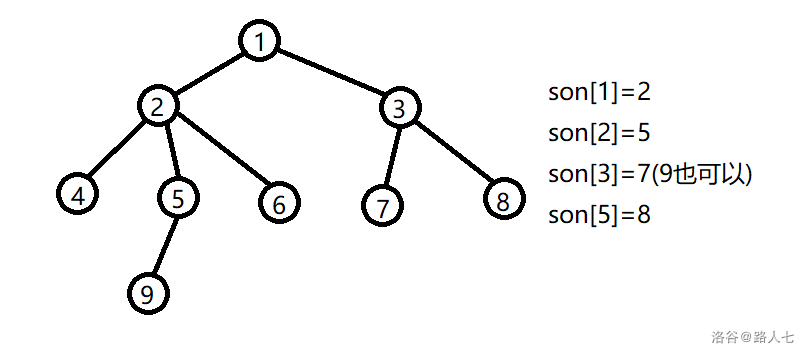
2. 重边：把两个重儿子连起来的边。对于剩下的边，称为轻边。
3. 重链：许多重边连在一起，形成的链叫做重链。
  
  例如：

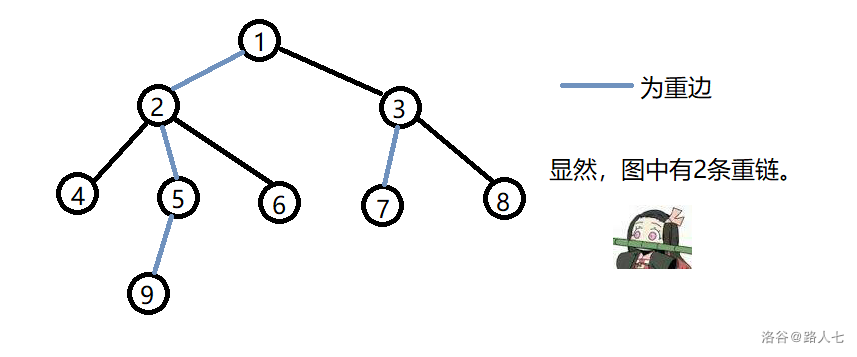
实现

所以，我们可以跑一个dfs，求出每个非叶子节点的重儿子。
```
int dfs1(int x,int pre,int dep)
{	
    deep[x]=dep;
    fa[x]=pre;
    tot[x]=1; //以x为根节点的子树的大小
    int maxson=-1;
    for(int i=f[x];i;i=e[i].nx)
    {	
        if(e[i].v==pre)continue;
        tot[x]+=dfs1(e[i].v,x,dep+1);
        //更新重儿子↓
        if(tot[e[i].v]>maxson){maxson=tot[e[i].v];son[x]=e[i].v;}
    }
    return tot[x];
}
```
接下来，我们要把点放在一个序列里。

然后就是dfs序，也是跑一个dfs。

但是，为了分别使重链上每个点在dfs序上连续出现，在dfs时加上几条语句：
1. 用\(top[x]\)记住x所在的重链的头部，若不在重链（轻边），记为自己。
2. 每次先跑重儿子
实现也很短：
```
void dfs2(int x,int tops)
{	
   idx[x]=++cnt; //记录x在序列中的位置
   top[x]=tops;
   a[cnt]=pw[x]; //pw[]为初始每个点的权值 cnt[]就是dfs序
   if(!son[x])return;
   dfs2(son[x],tops); //先跑重儿子
   for(int i=f[x];i;i=e[i].nx) //其他轻边
   {	
       if(idx[e[i].v])continue;
       dfs2(e[i].v,e[i].v);
   }
}
```
接下来，就要处理\(4\)种操作了。先看后面\(2\)种。

3.将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)

4.求以 \(x\) 为根节点的子树内所有节点值之和

很明显，任意一个节点x一定和它所有子节点在dfs序里连续出现。那么这两个操作可以直接用线段树处理。

那么前\(2\)个操作呢？

1.将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)

2.求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和

从\(x\)到\(y\)的最短路径只有一条，那么在在这条路径中，要在dfs序上加多少个区间？

按照之前的定义，重链上的点一定连续出现在dfs序上，所以，我们可以把 \(x\) , \(y\) 往上跳，即 \(x=top[x],y=top[y]\) , 直到 \(top[x]==top[y]\) 的时候停下来。

然后每次跳的时候，相应处理序列的值。

要注意的是，每次跳时，应选择重链的头更深的跳。

画图举例：

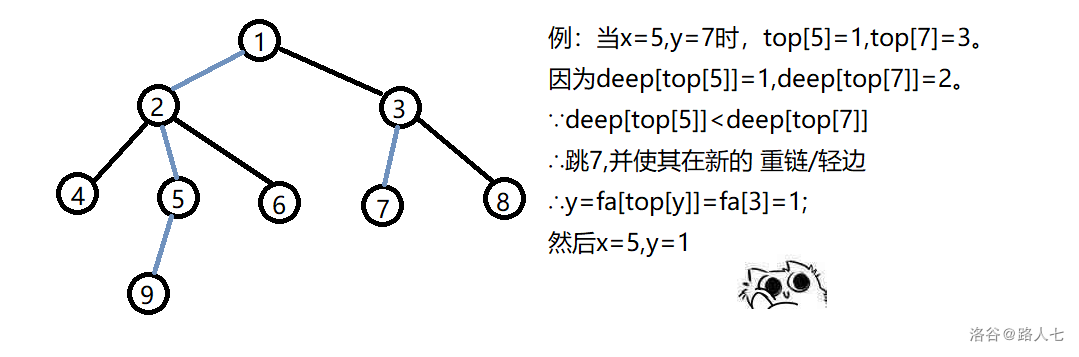
结束√

实现：
```
void treeadd(int x,int y,int val)//操作3
{	
    while(top[x]!=top[y])
    {	
        if(deep[top[x]]<deep[top[y]])swap(x,y);
        add(1,n,idx[top[x]],idx[x],val,1);
        x=fa[top[x]];
    }
    if(deep[x]>deep[y])swap(x,y);
    add(1,n,idx[x],idx[y],val,1);
}
```
```
int treesum(int x,int y)//操作4
{	
    int ans=0;
    while(top[x]!=top[y])
    {	
        if(deep[top[x]]<deep[top[y]])swap(x,y);
        ans=(ans+query(1,n,idx[top[x]],idx[x],1))%Mod;
        x=fa[top[x]];
    }
    if(deep[x]>deep[y])swap(x,y);
    ans=(ans+query(1,n,idx[x],idx[y],1))%Mod;
    return ans;
}
```

时间复杂度

有\(2\)个性质:
1. 若边 \((x,fa)\) 为轻边，则 \(size(x) \le \frac{size(u)}{2}\)
2. 树中任意 \(2\) 个节点之间的路径中，轻边不超过 \(log_2 n\)，重链不超过 \(log_2 n\)
在算上线段树复杂度 \(O(log^2 n)\)

完整代码

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int Maxn=1e5+5;
struct edge{
	int v,nx;
}e[Maxn<<1];
struct tree{
	int sum,lazy;
}t[Maxn<<2];
int n,m,ne,root,Mod,f[Maxn],pw[Maxn];
int deep[Maxn],fa[Maxn],son[Maxn],tot[Maxn];//dfs1 
int cnt,top[Maxn],idx[Maxn],a[Maxn];//dfs2  
void addedge(int u,int v)
{	
	e[++ne].v=v;
	e[ne].nx=f[u];
	f[u]=ne;
}
int dfs1(int x,int pre,int dep)
{	
	deep[x]=dep;
	fa[x]=pre;
	tot[x]=1;
	int maxson=-1;
	for(int i=f[x];i;i=e[i].nx)
	{	
		if(e[i].v==pre)continue;
		tot[x]+=dfs1(e[i].v,x,dep+1);
		if(tot[e[i].v]>maxson){maxson=tot[e[i].v];son[x]=e[i].v;}
	}
	return tot[x];
}
void dfs2(int x,int tops)
{	
	idx[x]=++cnt;
	top[x]=tops;
	a[cnt]=pw[x];
	if(!son[x])return;
	dfs2(son[x],tops);
	for(int i=f[x];i;i=e[i].nx)
	{	
		if(idx[e[i].v])continue;
		dfs2(e[i].v,e[i].v);
	}
}
void build(int l,int r,int k)
{	
	if(l==r)
	{	t[k].sum=a[l];t[k].lazy=0;
		return;
	}
	int mid=(l+r)>>1;
	build(l,mid,k<<1);
	build(mid+1,r,k<<1|1);
	t[k].sum=(t[k<<1].sum+t[k<<1|1].sum)%Mod;
	t[k].lazy=0;
}
void pushdown(int l,int r,int k)
{	
	int mid=(l+r)>>1;
	int x=t[k].lazy;
	t[k<<1].sum=(t[k<<1].sum+(mid-l+1)*x)%Mod;
	t[k<<1|1].sum=(t[k<<1|1].sum+(r-mid)*x)%Mod;
	t[k<<1].lazy=(t[k<<1].lazy+x)%Mod;
	t[k<<1|1].lazy=(t[k<<1|1].lazy+x)%Mod;
	t[k].lazy=0;
}
int query(int l,int r,int x,int y,int k)
{	
	if(x<=l&&r<=y)return t[k].sum;
	pushdown(l,r,k);
	int mid=(l+r)>>1;
	if(y<=mid)return query(l,mid,x,y,k<<1);
	if(x>mid)return query(mid+1,r,x,y,k<<1|1);
	return (query(l,mid,x,y,k<<1)+query(mid+1,r,x,y,k<<1|1))%Mod; 
}
void add(int l,int r,int x,int y,int z,int k)
{	
	if(x<=l&&r<=y)
	{	
		t[k].sum=(t[k].sum+(r-l+1)*z)%Mod;
		t[k].lazy=(t[k].lazy+z)%Mod;;
		return;
	}
	pushdown(l,r,k);
	int mid=(l+r)>>1;
	if(x<=mid)add(l,mid,x,y,z,k<<1);
	if(y>mid)add(mid+1,r,x,y,z,k<<1|1);
	t[k].sum=(t[k<<1].sum+t[k<<1|1].sum)%Mod;
}
void treeadd(int x,int y,int val)
{	
	while(top[x]!=top[y])
	{	
		if(deep[top[x]]<deep[top[y]])swap(x,y);
		add(1,n,idx[top[x]],idx[x],val,1);
		x=fa[top[x]];
	}
	if(deep[x]>deep[y])swap(x,y);
	add(1,n,idx[x],idx[y],val,1);
}
int treesum(int x,int y)
{	
	int ans=0;
	while(top[x]!=top[y])
	{	
		if(deep[top[x]]<deep[top[y]])swap(x,y);
		ans=(ans+query(1,n,idx[top[x]],idx[x],1))%Mod;
		x=fa[top[x]];
	}
	if(deep[x]>deep[y])swap(x,y);
	ans=(ans+query(1,n,idx[x],idx[y],1))%Mod;
	return ans;
}
int main()
{	
	scanf("%d%d%d%d",&n,&m,&root,&Mod);
	for(int i=1;i<=n;i++)
		scanf("%d",&pw[i]);
	for(int i=1;i<=n-1;i++)
	{	
		int u,v;
		scanf("%d%d",&u,&v);
		addedge(u,v);
		addedge(v,u);
	}
	dfs1(root,0,1);//找重儿子
	dfs2(root,root);//求序列 
	build(1,n,1);//线段树
	while(m--)
	{	
		int opt,x,y,z;
		scanf("%d",&opt);
		if(opt==1)
		{	
			scanf("%d%d%d",&x,&y,&z);
			treeadd(x,y,z);
		}
		if(opt==2)
		{	
			scanf("%d%d",&x,&y);
			printf("%d\n",treesum(x,y));
		}
		if(opt==3)
		{	
			scanf("%d%d",&x,&y);
			add(1,n,idx[x],idx[x]+tot[x]-1,y%Mod,1);
		}
		if(opt==4)
		{	
			scanf("%d",&x);
			printf("%d\n",query(1,n,idx[x],idx[x]+tot[x]-1,1));
		}
	}
	return 0;
}

\[\text{by Rainy7} \]

posted @ 2020-02-08 12:32 Rainy7 阅读(196) 评论(0) 编辑收藏举报

刷新页面返回顶部

Rainy7

随口的誓言，你要我怎么捡。

「树链剖分」学习笔记

公告