「凸包」学习笔记

• 前言

  未经允许，请勿转载。

凸包真难。

代码如果相似是因为我就是向别人学的。

（为什么没人讲向量..第一次学不懂向量然后代码硬是看不懂嘤嘤嘤..）

---

• 向量及运算的芝士(可能摘自很多地方..

  定义：有大小和方向的量，又称为矢量。

  坐标\(A(x_1,y_1),B(x_2,y_2)\)

  向量\(\overrightarrow{AB}=(x_2-x_1,y_2-y_1)\)

  加法：\((x_1+x_2,y_1+y_2)\)

  减法：\((x_1-x_2,y_1-y_2)\)

  点积：\(a·b=x_1x_2+y_1y_2\)

  1. \(a·b=0\) 则\(a \perp b\)
  2. \(a·b<0\) 则他们的夹角大于90
  3. \(a·b>0\) 则他们的夹角小于90

  叉积：\(a×b=x_1y_2-x_2y_1\)

  1. 若\(a×b=0\)则\(a\)与\(b\)共线(可以反向)
  2. 若\(a×b>0\)则\(b\)在\(a\)逆时针方向
  3. 若\(a×b<0\)则\(b\)在\(a\)顺时针方向

---

• 有啥用？求什么

  给出一堆点，再用一根绳子包住，这就是个凸包啦。

  然后一般问绳子的长度。

---

• 如何实现？

  主要分为2部：求上半部分和下半部分。

  首先，先对每一个点以\(x\)坐标从小到大排序，如果一样再以\(y\)坐标从小到大排序。

  比如上面那个例子：

  

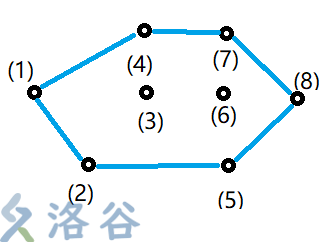
  先初始化把\((1)(2)\)放入栈中，此时栈中有\((1)(2)\)

  然后把\((3)\)放入栈中，此时栈中有\((1)(2)\)

  因为此时在求下半部分，因此\((3)\)我们希望越下越好，即\(\overrightarrow{(1)(2)}×\overrightarrow{(2)(3)} \geqslant0\)，(叉积的定义),然后可以发现\((3)\)是满足的:

  

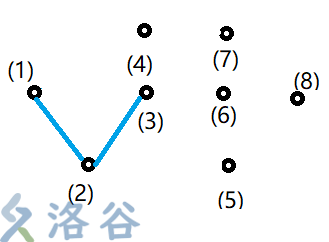
  所以栈不改变，栈中有\((1)(2)(3)\)

  然后,把\((4)\)放入栈中，\((4)\)满足\(\overrightarrow{(2)(3)}×\overrightarrow{(3)(4)} \geqslant0\)，所以栈不改变:\((1)(2)(3)(4)\)。

  

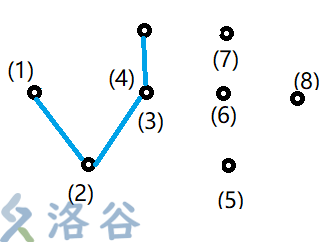
  然后把\((5)\)放入栈中，发现\((5)\)不满足\(\overrightarrow{(3)(4)}×\overrightarrow{(4)(5)} \geqslant0\)，所以把\((4)\)弹出栈。

  而出栈后发现，\((5)\)仍不满足\(\overrightarrow{(2)(3)}×\overrightarrow{(3)(5)} \geqslant0\)，所以把\((3)\)踢出栈。此时栈中剩下:\((1)(2)(5)\)。

  

  把\((6)\)放入栈，\((6)\)满足\(\overrightarrow{(2)(5)}×\overrightarrow{(5)(6)} \geqslant0\)，不改变栈：\((1)(2)(5)(6)\)。

  

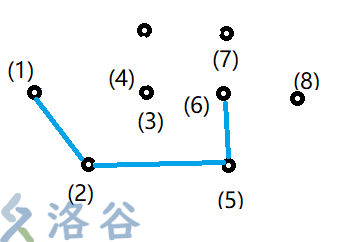
  把\((7)\)放入栈，\((7)\)满足\(\overrightarrow{(5)(6)}×\overrightarrow{(6)(7)} \geqslant0\)，不改变栈：\((1)(2)(5)(6)(7)\)。

  注：可能画歪了..\((6)(7)\)的\(y\)坐标相同。

  

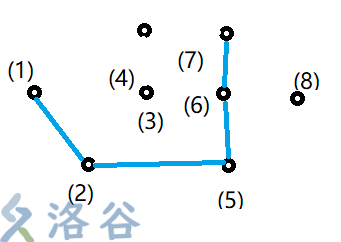
  把\((8)\)放入栈，\((8)\)不满足\(\overrightarrow{(6)(7)}×\overrightarrow{(7)(8)} \geqslant0\)，所以把\((7)\)踢出：\((1)(2)(5)(6)(8)\)。

  但是发现，此时仍不满足\(\overrightarrow{(5)(6)}×\overrightarrow{(6)(8)} \geqslant0\)，所以再把\((6)\)踢出，栈中剩下：\((1)(2)(5)(8)\)。

  

  这样，下部分的凸包就完成啦，而上部分再反着做一遍就好了。

---

• 代码

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct point{
	double x,y;
}p[100010];
int n,sta[100010],cnt;
double ans;
point getvec(point a,point b){return point{(b.x-a.x),(b.y-a.y)};}
double dis(point a,point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
double xmul(point a,point b){return a.x*b.y-a.y*b.x;}
bool cmp(point a,point b)
{	
		if(a.x==b.x)return a.y<b.y;
		return a.x<b.x;
}
int main()
{	
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%lf%lf",&p[i].x,&p[i].y);
		sort(p+1,p+1+n,cmp);
		sta[++cnt]=1;sta[++cnt]=2;
		for(int i=3;i<=n;i++)
		{	
			point u=getvec(p[sta[cnt-1]],p[sta[cnt]]);
			point v=getvec(p[sta[cnt]],p[i]);
			while(xmul(u,v)<0.0)
			{	
				if(cnt==1)break;
				cnt--;
				u=getvec(p[sta[cnt-1]],p[sta[cnt]]);
				v=getvec(p[sta[cnt]],p[i]);
			}
			sta[++cnt]=i;
		}
		int tmp=cnt;
		sta[++cnt]=n;sta[++cnt]=n-1;
		for(int i=n-2;i>=1;i--)
		{	
			point u=getvec(p[sta[cnt-1]],p[sta[cnt]]);
			point v=getvec(p[sta[cnt]],p[i]);
			while(xmul(u,v)<0.0)
			{	
				if(cnt==tmp+1)break;
				cnt--;
				u=getvec(p[sta[cnt-1]],p[sta[cnt]]);
				v=getvec(p[sta[cnt]],p[i]);
			}
			sta[++cnt]=i;
		}
		for(int i=1;i<=cnt-1;i++)
			ans+=dis(p[sta[i]],p[sta[i+1]]);
		printf("%.2lf\n",ans); 
		return 0;
}