2024.2 & 4 做题记录

省流：因为一月底回厦门玩然后又回泉州过年，直到 2.17 才开始做题。

[APIO2018] 铁人两项

圆方树和后缀数组我都想开个贴单独写。考虑关于“简单路径”，在点双上都有很特殊的性质。考虑把原图的圆方树建出来，然后考虑简单路径和圆方树的关系。

注意到，在同一点双的两点的简单路径的并集，恰好为整个点双，也就是说，对于两圆点在树上的路径中方点的相邻原点的并集也就是两点间所有简单路径经过点的并集。

枚举起点终点 \(s, f\)，合法中间点 \(c\) 的数量为并集 \(-2\)（去掉起点和终点）。那么计算答案就好计算了，我们给方点赋值为相邻圆点数量，圆点赋值为 \(-1\)，问题转化为两点路径权值和。

为什么这样是对的？
按照刚刚的赋值方式，我们在经过一个点双时会正好把点双的大小 \(-2\) 算进去，\(-1+sz_u-1\)。但是因为在圆方树中任意圆点相邻的都是方点，而又因为是路径，所以一个圆点又会被两个方点贡献，那么贡献又回到了 \(1\)。
但是起点和终点不会被两个方点相邻，所以它们的贡献也确实就是 \(-1\)，那么总的贡献就正确了。

现在复杂度是 \(O(n^2)\)，怎么办？

转化思路，我们统计每个点的贡献，这是好做的，dp 就是一个乘法原理，注意只能统计圆点的贡献方案。

Tourists

套路的变成圆方树，那么也可以把所有相邻原点的权取 \(\min\) 挂到方点上，直接查询路径最小值即可。

考虑修改，这样做要把该圆点所有相邻的方点做出修改，于是我们对于每个方点改为只记录其儿子的贡献，这样用树剖和线段树就可以维护了，同时对于每个方点维护一个 multiset。维护指定值删除和最小值。

https://www.luogu.com.cn/discuss/780218

Count on a tree

不太难。因为主席树天生是一个支持前缀和的东西，所以我们直接像记录树上前缀和一样，把链从上至下当作是序列，然后对于主席树上也有的差分，有

\[s_u + s_v - s_{lca(u, v)} - s_{fa_{lca(u, v)}} \]

作为查询版本，之后直接主席树二分即可。我倒是觉得这个式子没什么好解释的。

压力

这题太纯了，直接秒了，做也是一遍过。因为一个点能成为割点一定是“所有简单路径必须经过的点”，也跟圆方树很有关系，于是考虑建出原图的圆方树。不难发现，一条路径上涉及到的所有的圆点都是必须经过的，直接树上差分即可。

我确实觉得这是个很直觉的东西，不过我还是应该感性写一下理解。
如果我们经过某个方点控制的圆点，然后走出了这个点双，也就是说下一步的点就不属于当前点双了（如果有多条路径当前点双就不是极大点双），那也就是说这是唯一路径，也就是说这是割点。
证毕。

[JSOI2007] 字符加密

最秒的一集，首先断环成链肯定是有必要的，然后发现直接后缀数组就是题目里要的东西，就通关了。

[NOI2016] 优秀的拆分

设 \(a_i\) 为以 \(i\) 结尾的形似 AA 的串的个数，\(b_i\) 为以 \(i\) 开头的形似 AA 开头的个数。答案就是 \(\displaystyle\sum^{n-1}_{i=1} a_ib_{i+1}\)。

考虑咋算 \(a, b\)。我们枚举 AA 串的长度，然后从 \(s_len\) 开始每隔 \(len\) 撒点，不难发现每个 AA 串必然经过两个关键点。考虑从关键点上算贡献。

我们求出相邻关键点的 lcp 和 lcs，发现当 lcp + lcs \(< len\)，相邻两段拼起来还是有一段不相同的部分，这代表这部分不是答案。

当 lcp + lcs \(\ge len\) 时。这个时候 lcp 和 lcs 可以拼成 AA。并且不只一种方案。

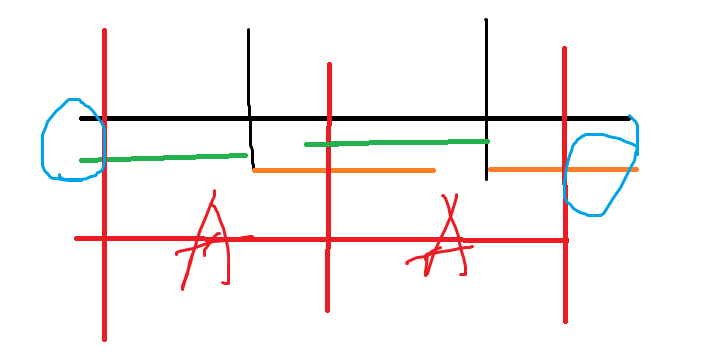
红线的 AA 是一种方案，但是我们在蓝色范围内滑动一样可以构成合法串，这部分蓝色的其实就是 lcp + lcs - len，即重叠部分长度。

于是前半部分蓝色都可以作为开头，后半部分都可以作为结尾。差分区间 \(+1\) 即可。对于快速求 lcp, lcs 考虑后缀数组，正反维护两个 SA。

时间复杂度在枚举长度为调和级数，\(O(n \log n)\)。

---

省流：二月份别的题都不写了，三月份文化课，所以直接快进到四月份做题记录。

P3586 [POI2015] LOG

对于询问：\(y\) 次 \(x\)。

考虑对于所有 \(a_i < y\)，这些数最多贡献 \(a_i\)；对于 \(a_i \ge y\) 的数贡献为 \(y\)，值域线段树维护数字个数以及和，判断 \(sum \ge xy\) 是否成立即可。

事实上我觉得还需要判掉全局非零数是否 \(\ge x\) 个，不过没判也过了。

离散化。

谜之阶乘

设 \(d = a - b\)，考虑阶乘的增长速度非常快，所以 \(d\) 肯定不大。

\(20!=2,432,902,008,176,640,000 > 1,000,000,000,000,000,000\)

枚举 \(d\)，发现阶乘大小具有单调性，所以二分阶乘段起点即可。

P4137 Rmq Problem / mex

考虑对于 mex，添加不是好做的，但是删除只需要维护一个桶，到 \(0\) 时更新答案即可。所以用回滚（不添加）莫队维护，即可。

P5901 [IOI2009] Regions

发现 每种颜色的数量 和 颜色的数量 成反比例，所以考虑把东西规约到根号上。

对于一种颜色，\(c_x\) 表示颜色为 \(x\) 的点的数量。

• 当 \(c_x \ge \sqrt{n}\) 。

我们考虑分别对于 \(r1 = x, r2 = x\) 的每种颜色暴力算出对应的答案。具体来说，当 \(r1 = x\)，问题变每个 \(x\) 点子树内各颜色的数量，等价于对于每个点统计其到根的路径上 \(x\) 点的数量，dfs 同时记录前缀和即可；当 \(r2 = x\) 时，问题即为每个点子树内 \(x\) 点数量，类似子树统计即可。

复杂度全在预处理，为 \(O(n^{1.5})\)。

• 当 \(c_x < \sqrt{n}\)

当两种点数量都不多时，考虑暴力把每个点插到树状数组里，然后对于每个点暴力查，最后再撤销即可。

复杂度 \(O(\sqrt{n}\log n)\)。

总复杂度 \(O(n^{1.5} + q\sqrt{n}\log n) = O(q\sqrt{n}\log n)\)。

P3705 [SDOI2017] 新生舞会

抽象为二分图匹配。

分数规划类问题直接考虑二分，推式子后两点匹配边权即为 \(a_{i, j} - mid \times b_{i, j}\)，跑最大费用最大流，如果能在 \(cost \ge 0\) 的情况下满流即可行。

P4688 [Ynoi2016] 掉进兔子洞

按照题目里的做法，其实答案就是 \(\displaystyle\sum_{i = 1}^m r_i - l_i + 1 - 3k\)，其中 \(k\) 是 每一种数，同时在三个区间出现的最小次数 之和。

考虑对 \(\{a\}\) 离散化，用 bitset 维护这个东西，注意到对于 \(x, y\) 分别为离散化前值和数量，bitset 内 \([x, x + y - 1]\) 都是 \(1\)，之后把三个区间的 bitset & 起来就是答案了，注意到空间开不下，还需要对询问分块处理。

P1402 酒店之王

考虑房间和菜分别对应着两个二分图，建完图直接跑最大流就行，注意对房间或者菜拆点，控制流量 \(\le 1\)。

P9809 [SHOI2006] 作业 Homework

根号分治。

对于 \(P \le \sqrt{V}\)，暴力处理，每次重构所有数字关于这 \(\sqrt{V}\) 个数的答案。

对于 \(P > \sqrt{V}\)，注意到这部分的数字模完之后比较近的 \(iP\) 最多只有 \(\sqrt{V}\) 个，考虑用 set 维护所有数，枚举 \(iP\) 然后在 set 里二分最小值。

其实不是正解，但还是无耻加入了 \(O(q\sqrt{n}\log n)\)。

[ARC125E] Snack

朴素的网络流模型很简单。

• 从 \(S\) 向所有零食连流量是 \(a_i\) 的边。
• 从所有零食向所有小孩连流量是 \(b_i\) 的边。
• 从所有小孩向 \(T\) 连流量是 \(c_i\) 的边。

注意到第二步涉及到 \(nm\) 条边，复杂度 \(O(n^{1.5}m)\)，过不去。

注意到最大流同时等于最小割，所以尝试换到最小割的视角考虑。

那么问题变为将原图割为不连通的两部分，求最小割掉的权值。那么对于 \(a, b, c\) 三种类型的边不妨先枚举其中一种的边的情况。

我们枚举有 \(k\) 个零食最终会被割到 \(S\) 集合，显然一定会选择最小的 \(k\) 个 \(a_i\) 割掉。现在考虑每个小孩，如果想割到 \(T\)，需要把原本未被钦定割到 \(S\) 的 \(n - k\) 的零食向他连的边全割掉，权值为 \((n - k)b_i\)；同时，如果向割到 \(S\) 只需要割掉 \(c_i\) 即可。

注意到关于 \(a_i\) 的部分是确定的，关键在于维护每个小孩的 \(\min(kb_i, c_i)\)。即为一个一次函数和一个常函数的取值问题，按照 \(\dfrac{c_i}{b_i}\) 排序，显然具有单调性，双指针维护即可。

code

P3515 [POI2011] Lightning Conductor

先变一下原式：

\[a_j\le a_i+p-\sqrt{|i-j|}, j \in [1, n] \]

\[p \ge a_j - a_i + \sqrt{|i-j|} \]

因为要使得 \(p\) 最小且为整数，所以有

\[p = \max_{j = 1}^n\bigg\{a_j + \left \lceil \sqrt{|i-j|} \right \rceil \bigg \} - a_i \]

形式类似于 1D/1D 的转移，并且满足决策单调性。

\(C(i, j) = \sqrt{|i-j|}\)。
有 \(a \le b \le c \le d\)，即证满足四边形不等式，有

\[C(a, c) + C(b, d) > C(a, d) + C(b, c) \]

\[\sqrt{c - a} + \sqrt{d - b} > \sqrt{d - a} + \sqrt{c - b} \]

\[(c - a) + (d - b) + 2\sqrt{(c - a)(d - b)} > (d - a) + (c - b) + 2\sqrt{(d - a)(c - b)} \]

\[\sqrt{(c - a)(d - b)} > \sqrt{(d - a)(c - b)} \]

\[(c - a)(d - b) > (d - a)(c - b) \]

\[cd - ad - bc + ab > cd - ac-bd + ab \]

\[-ad-bc>-ac-bd \]

\[ad+bc<ac+bd \]

\[a(d - c) < b(d - c) \]

显然 \(a < b\)，证毕。

证法 2，来自 Liuxizai 的博客。

\[\sqrt{c - a} + \sqrt{d - b} > \sqrt{d - a} + \sqrt{c - b} \]

\[\sqrt{d - b} +\sqrt{c - b} > \sqrt{d - a} + \sqrt{c - a} \]

设 \(f(x) = \sqrt{x + (d - c)} + \sqrt{x}\)，则原等价于证

\[f(c-b) > f(c-a) \]

因为 \((\sqrt{x})'\) 单调递减，所以 \((\sqrt{x + (d - c)})' < (\sqrt{x})'\)，所以 \(f(x)'<0\)，所以 \(f(x)\) 单调递减。
因为 \(c - b < c - a\)，所以 \(f(c - b) > f(c - a)\)。
证毕。

所以原式决策点单调不降，且 \(p_i\) 独立，分治计算。

另外，分治时不会计算到 \(p_1\)，所以应该将原数组翻转计算两遍。

P4602 [CTSC2018] 混合果汁

答案可以二分，每次 check 当最小值为 \(mid\) 时能否选出一些果汁满足要求，显然当范围确定时我们会贪心的先选择便宜的果汁，因为这样意味着获得的升数最多，这个选择的过程可以考虑对价格建立主席树然后二分完成，复杂度即为 \(O(m \log n \log V)\)。

CF526F Pudding Monsters

因为 \(k \times k\) 的矩阵内恰好有 \(k\) 个棋子，且每列只有一个，那么选择的这连续段必须满足它们的 \(x\) 是连续的，即如果存在 \(\{a\}\) 满足对于给出的 \((x, y)\) 上有棋子，有 \(a_x = y\)，那么要求的即为全局满足值域是连续段的连续段。等价于 \(\max - \min + 1 = r - l + 1\)，即 \(\max - \min - r + l = 0\)。

首先考虑枚举右端点，对于每个左端点维护出 \(\max - \min - r + l\) 的值，其中 \(l\) 为定值，不随右端点改变而改变，\(r\) 每次随着右端点 \(+1\) 贡献 \(-1\)，即线段树上全局 \(-1\)。

考虑 \(\max, \min\)，考虑 \(a_r\) 会影响到的区间，这个可以用单调栈维护，对于区间补上差即可。对于统计，因为在 \([r, r]\) 的叶子一定满足 \(\max - \min - r + l = 0\)，所以维护 \(0\) 的数量等价于维护最小值的数量（最小值一定为 \(0\) 且存在），直接维护即可。