6.7总结

传送门
更差的阅读体验

T1 午餐

咕咕咕咕咕咕

T2 Removing Coins

看到T2，是个博弈论，没见过树上的，于是想到在数列里的博弈论，又联想到树的特殊形式————链。

于是我们来讨论一下链的情况（对于没有硬币的点，我们就视为它被删掉了）：

讨论链的情况

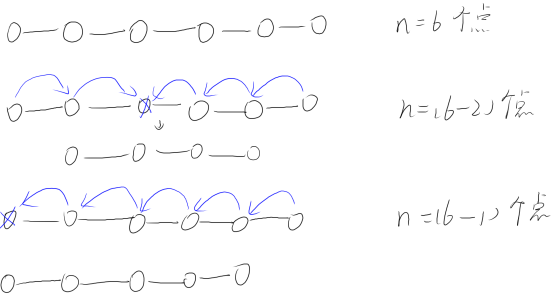
发现若是选择两端的点，顶点数会减一；若是选择中间的点，顶点数会减二。

现在我们站在链的角度来思考在树上选择的情况，一颗树可以看成一条链且在某些顶点上有分支的图。我们再来以这种方式来选点找找规律，发现树上的点删着删着最后总会变成一条链，且这条链是最长链的子链，于是我们把看这棵树的形式转换为其最长链（直径）且在某些顶点上有分支的图：

例子

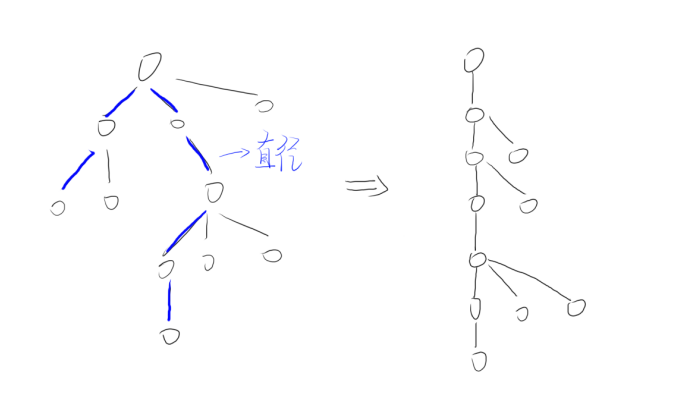
通过手玩这个例子后发现，我们若是选最长链两端的点，最长链顶点数会减一；若是选择非最长链两端的点，最长链顶点数会减二，其余的分支会因为持续的选点而被删完。

所以发现，在树上的问题被我们转化成了在链上的问题，妙哉！

讨论完了删点的变化情况，我们再来讨论一下必胜条件：若最长链上有 \(i-1\) 和 \(i-2\) 个点时均必胜，则最长链上有 \(i\) 个点时必败，否则必胜，特殊的，若最长链上有 \(1\) 个点时必胜，有 \(2\) 个点时必败。
打表发现用树的最长链上点的个数 \(\mod 3\) ，若等于 2 后手胜，否则先手胜。

T3 大师

一眼DP，状态设为 \(f_{i,j}\)，表示从结尾为 \(i\) 的公差为 \(j\) 的等差数列数量，于是状态转移方程为：

\[f_{i,a_i-a_j} = f_{i,a_i-a_j} + f_{j,a_i-a_j}\times 1 + 1(1\le j< i) \]

在求 \(f\) 时顺便记录 \(ans\) 即可，时间复杂度 \(O(n^2)\)。

T4 绝世好题

一眼DP，本来想的是设 \(f_{i}\) 表示以 \(a_i\) 为结尾的 \(b\) 数列最大长度。但是时间会爆炸(\(O(n^2)\))。

换个方向考虑，以二进制数位进行转移，设 \(f_i\) 表示当前数用二进制表示的第 \(i\) 位为 \(1\) 的最大长度，则转移方程为：

\[f_j = max(f_j, (f_k + 1)[(a_i>>k)\&1==1])((a_i>>j)\&1==1) \]

T5 Median Pyramid Hard

考虑二分答案。

为什么是二分答案？是因为我们二分的是顶层的数是否 \(>k\)，其具有单调性，所以可以二分。

二分答案的核心部分为 \(check\) 函数，所以我们来看 \(check\) 怎么写。
先把数列中 \(>k\) 的看做 \(1\)，\(<k\) 的看做 \(0\)，再来手玩一下：

情况1：中间点在一个连续段里。
情况2：底部为形如 \(01010\dots 101\) 的 \(01\) 串构成。
情况3：中间点不在连续段里，且底部有且仅有一个连续段。
情况4：中间点不在连续段里，且底部有且不止一个连续段。

情况（看图理解即可）

于是这道题就切掉啦~（膜拜lyx，lyx好闪）