JOISC 2023 简要题解
为什么我只会一堆大众题啊!!
还没更完的:???
Day1 T1
显然取链上代价前最小的若干个付银币,于是主席树上二分即可。
Day1 T2
首先想一个 dp 做法出来。
考虑做一个线头 dp 类似的东西。从左到右扫,状态中记录现在还没有结束的线头个数。
仔细思考一下,要记录还未结束的线头个数和 Optimal 策略 下还未结束的线头个数,状态数为 \(n^3\)。
发现有一维度不用计入状态,只需要乘上系数,状态数变成 \(n^2\)。 好像有点问题
其实是乘一个组合数。等一下补一下详细的。
设 \(f(i,j,k,0/1/2)\) 表示决定了前 \(i\) 个位置,设 optimal 策略下最后一个选的线段结束位置为 \(p\),有 \(j\) 个插头在 \(p\) 前开始(无用插头),\(k\) 个插头在 \(p\) 后开始(有用插头)
\(0\) 表示 fake 策略没有少 1,并且 fake 策略下没有可用的插头。
\(1\) 表示 fake 策略少了 1,并且 fake 策略下有可用的插头。(没有就直接寄了)
\(2\) 表示 fake 策略没有少 1,并且 fake 策略下有可用的插头。
转移分类讨论,答案用总数减去不合法的。
然后发现 \(j\) 这一维度完全可以不用计入状态:某次转移如果出现了 \(x\) 个无用插头,直接在后面选 \(x\) 个插头钦定给它们,乘一个组合数,转移到 \(f(i+x,0,..)\)。
卡一卡上下界的常就能通过。
(为什么 cf comment 说有更好的做法啊,顶真吗?)
Day1 T3
想了很久这题不会,又想了很久发现是原题...
首先有一些基础的思考,比如一个点 \(u\) 能一步跳到 \(v\) 的话就可以松弛 \(ans_v+1 \to ans_u\)。现在的问题就是对于每个点 \(u\) 算出跳到 \(1\) 和 \(n\) 的最小步数(跳到 \(1,n\) 就相当于跳到所有点)。
然后发现要求的就是 这题,于是线段树优化建图就做完了。
Day2 T1
看错题意以为会一直移动,然后卡了很久。。。。。。。
询问次数是 \(\log\) 的,这启发我们想一些一次询问出某个比例的边的做法。
对于第一次:把所有点按照 \(dep\bmod 3\) 分成 3 类,对于某一类的点全部放上球然后询问。容易发现这样不同层的球移动不会互相影响,就可以问出 \(cnt\) 条边。取最多个数的一类,则 \(cnt\ge n/3\)。
接下来的每一轮,取三个类中 还有出边没问出来的点 最多 的一类,放上球然后询问。每次都至少问出三分之一的出边。
询问次数是 \(\lceil\log_3 n\rceil\le 29\)。
Day2 T2
对于去掉每个人 \(i\),有一些类是再去掉一票就寄了的,有一些类是再去掉一票也贡献不变的。
设每个 \(i\) 删掉它会对哪些集合票数减 0 的集合为 \(msk_i\)。那就是询问一个集合 \(T\),求出 \(\max_{j\ne i}(\text{popcount}(T\&msk_j))\)。
先子集和再超集和就可以处理。
Day2 T3
首先有一个每次都暴力 DP 的做法,但这样太暴力了,很难用数据结构维护,也很难区间询问。
于是尝试发现一些可以维护的性质/贪心结论。
发现小的一段长度一定为 \(1\),大的一段长度一定 \(\le 2\log V\),不然一定不优。
如果直接在线段树上维护(记录两端的大段长度),可以获得 \(Q\log n\log^3 V\) 的做法,和暴力一个分
然后想一想可以贪心的性质/结论。下面“取一个数”指将一个数作为小段。设 \(T=2\log V\),就是大段的最长可能长度。
设 \(f(i)\) 表示 \(j<i\),\(j\) 和 \(i\) 能同时取,且 \(j\) 最大的那个位置。
设 \(nxt(i)\) 表示最小的 \(j(j>i)\) 使得 \(f(j)\ge i\)。如果 \(nxt(i)>i+V\) 则设 \(nxt(i)=i+V\),对答案没有影响。
容易发现如果当前小段选的是 \(i\),下一个小段一定可以贪心选 \(nxt(i)\)。(如果选了 \(nxt(i)\) 不满足可以调整 \(i\))
枚举开头的一个点 \(i(i\in [l,l+T])\),不断跳 \(i\to nxt(i)\to nxt(nxt(i))...\) 表示我们选小段的最后一个位置。
从 \(i\) 跳到 \(r\) 附近的一个点 \(x(x\in [r-T,r])\),然后判一堆边界情况,计算一下答案。
边界情况太恶心了,对拍出一堆边界情况。。解释不清楚,建议直接看代码
修改的时候,容易发现只有 \(O(\log V)\) 个点的 \(nxt\) 会被修改。并且 \(nxt\) 构成一棵树,可以直接用 LCT 维护树。
复杂度 \(Q\log V(\log V+\log N)\)。
Day3 T1
首先画出一条折线,A 向右上方走一格,B 向右下方走一格。
交换两个 A,B 可以看作把折线的某个位置从“下上”翻成了“上下”。
把一条折线变成另一条折线的代价就是两条折线之间的面积。
经过一些贪心、手玩可以发现,就是把一条初始的折线经过若干次向上翻后,可以包含住 \(m\) 个“峰”。下图是一种 \(m=3\) 的情况,黄色部分为翻上去的代价。
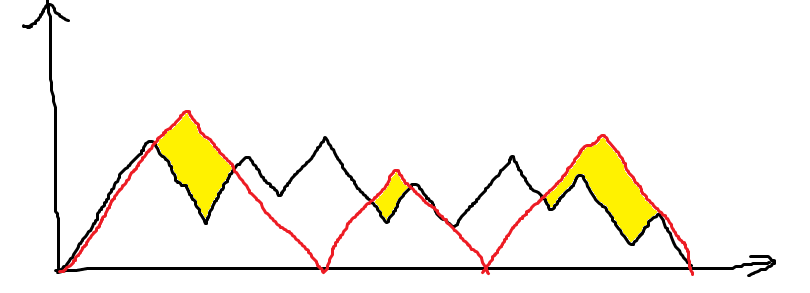
然后就可以写出 dp,设 \(f_{i,j}\) 为第 \(j\) 个峰的结束位置是 \(i\) 的代价。
转移是 \(f_{i,k}+cost(i,j)\to f(j,k+1)\)。\(cost\) 就是上图黄色的面积,可以预处理以后 \(O(1)\) 计算。
然后突然发现 dp 的第二维是有凸性的!于是可以 wqs 二分。
发现转移是有决策单调性的,直接类似 [IOI2000] 邮局 做,就可以 \(O(n\log n\log V)\)。评测机很慢,过不太去,只有 87 分。
但上面那个做法实在是脑子傻了,发现转移分讨一下就可以斜率优化了,一次 dp 为 \(O(n)\),时间复杂度 \(O(n\log V)\)。
Day3 T2
经过一些猜猜猜交交交,发现 在可行的情况下,选大的 box 越多就是越好的。
可以写出一个 DP,设 \(dp_{t,i,j}\) 表示考虑了前 \(t\) 大的 box,选了 \(i\) 个 box,放了 \(j\) 个 cookies 是否可行。
复杂度是 \(n^3\) 的,经过一些循环卡上下界可以跑 \(n=3000\) 获得 85pts
我错了,这个复杂度是 \(n^2\log n\) 而不是 \(n^3\):由于是从大到小加 box,所以“选了 \(i\) 个 box”这一维只需要转移到 \(n/b_i\) 的。这一维总转移最多就是 \(n/n+n/(n-1)+..+n/1 = n\ln n\)。
然后加上 bitset 优化,就可以做到 \(\frac{n^2\log n}{w}+n^2\),可以通过。
Day3 T3
我的做法太垃圾了。
要求出一个区间内点的虚树包含的边集大小。
根据[ZJOI2019]语言,两颗 dfs 序不相交的虚树是可以合并边集大小的信息的。
设 \(s,t\) 为 dfs 序最大、最小的点,那么
s=l.s
t=r.t
val=l.val+r.val-Dep(Lca(l.t,r.s))
看做平面上有 \(m\) 个点 \((i,dfn_{a_i})\)。
发现就是询问一个矩形内的信息并,并且是有顺序(按 dfs 序合并)的信息并。可以直接用 CF1375H trick 处理(分块+分治),时间复杂度 \(O(n\sqrt n)\)。
不过显然有更简单的做法。
扫描线右端点,然后每次加一个点就是在 LCT 上 Access 一下,把每个颜色段都修改一下。
复杂度 \(O(n\log^2 n)\)。
Day4 T1
通信题。主要是要还原 \(x,y\) 的信息。
可以选一些位置钦定来表示 \(x,y\) 的信息。在每种情况下,钦定的部分 一些位置会被 ban,一些位置可以填,在可以填的位置编一个属于这种 \(x,y\) 的 pattern。需要编的 pattern 在任何情况下都不冲突,这样 Bob 可以解码出 \(x,y\)。
但这样还是占用了比较多的格子。可以在 钦定的部分 里有一些表示 \(x,y\),有一些表示 \(S\),还是要求任意两个方案不冲突。
选对角线相关的格子应该能卡到 \(n=42\)。
zky 说他选的是左上角 3*4 的格子,可以卡到 \(n=43\)。
Day4 T2
对于树的做法:
答案是所有边权的 \(w_x+w_y\),加上最大的 \(w_i\),减去所有的 \(w_i\)。
\(Q=0\) 就是最小生成树。
现在解决 \(Q>0\) 的情况,就是在原树上砍 \(k\) 条边,加 \(k\) 条边,使得代价最小。
由于一定会把每个连通块的最小连到全局最小,这就相当于 让割开后的每个连通块 \(\sum \min w_i\) + 没割掉的边权 最小。
考虑给割开后的每个连通块“定一个根”,并且让根为连通块权值最小的点时答案最小。
把每条边看做两条边,\(x\to y\) 边权为 \(w_y\),\(y\to x\) 边权为 \(w_x\),然后生成一棵内向有根树。
定一个根后,把每条边的贡献看作父亲的点权。答案就是所有边父亲的点权加上所有点的点权(这样恰好是每条边的边权+根的点权)。容易发现这样的答案下,根选权值最小的点答案最小。
把每条边看作两条有向边。于是就转化成了 \(k-\) 最小有向生成森林的问题,可以直接用最小树形图的算法解决!
具体可以看 2020 集训队论文 张哲宇,最小内向森林问题。网上的blog
复杂度 1log。
Day4 T3
折返的次数是 \(\log V\),直接暴力找折返就是 \(n\log n\log V\)。
也可以用值域分段 trick 变成 \(n\log V\)。

