双极定向 / Ear Decomposition

用的太多了，不如记下来。

双极定向 - 方法 1

以 \(s\) 为根求出 dfs 树，求出每个点的 \(fa(u)\) 和 \(low(u)\)（最浅能到达的祖先）。

在每个点开一个列表，每次剥掉一个叶子，把该叶子加入 \(fa(u)\) 和 \(low(u)\) 的列表末尾，表示染黑了 \(fa(u)\) 或 \(low(u)\) 后就可以染黑 \(u\)。这样若一个点染黑，则可以将其列表里的点依次染黑，不断递归下去。

假设要求 \(s\to t\) 的双极定向。提取 \(s\to t\) 的路径，在剥叶子的过程中，不剥掉这条路径上的点。然后将路径从 \(s\to t\) 依次染黑，并且递归染黑其列表。

https://qoj.ac/submission/446860

双极定向 - 方法 2

这里考虑将所有边定向。

先以 \(s\) 为根求出 dfs 树，然后将 \(s\to t\) 的路径定向成“向下”。

我们先把 \(t\) 推进队列里，并把它标记为“向下”（向队列中加入 \((t,\downarrow)\)）。

从队列里取出一个点 \(t\)，然后不断向上爬祖先，把 \(t\) 到某个祖先都标记成相应的方向，直到碰到一个标记过的祖先边结束。

假设我们当前定向了 \((x,y)\) 这条边。这时碰到一条返祖边 \((x,u)\) 且 \(u\) 在 \(y\) 的子树中（重要细节：不要考虑 \(u\) 不在 \(y\) 子树中的返祖边）。此时需要给这条返祖边 \((x,u)\) 定向成 \((x,y)\) 相同的方向，然后将 \(u\) 向上的一段树边路径定向成 \((x,y)\) 相反的方向。

把 \(u\) 和这个对应方向推进队列里（比如下图就是加入 \((u,\uparrow)\)），不断 bfs 即可。

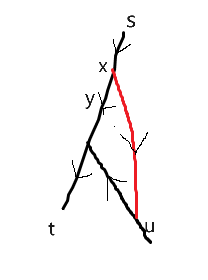
我们发现这个过程相当于加入了一个“耳”。

具体实现的话，假设返祖边 \((x,u)\) 对应路径 \(x\to y\to \dots \to u\)，将这条返祖边加入 \(y\) 的列表。定向树边 \((x,y)\) 时遍历一下 \(y\) 的列表即可。

https://codeforces.com/contest/730/submission/257809370

Ear Decomposition

假设我们当前有一个点 \(s\)，想要找出图的一个耳分解，使得：初始点集是 \(\{s\}\)，每次加入一个耳（开头和结尾都要在点集中）。

以 \(s\) 为根求 dfs 树，随便找一条 \(s\) 开始的非树边，设为 \((s,t)\)。

然后使用方法 2 求 \(s\to t\) 的双极定向。从 \(s\to t\to s\) 的路径即为一个 \(s\to s\) 的环，也就是第一个耳。在方法 2 的过程中，我们每次都会加入一个“耳”，所以自然求出了耳分解。

暂且不知道方法 1（剥叶子）能不能做。 我觉得求出双极定向后，随便从 \(s\to t\) 的点开始 dfs 一下就可以。