THUPC 2023 G&I 不是题解
开坑?
G
题意可以省去 1 操作,因为使用 2 操作替代(可以放在另一堆然后执行 2)
首先这个要求构造就很有迷惑性,尝试找性质却发现做不出来。
考虑全局的问题,枚举最后一对被消除的是什么牌。
然后发现了一个子问题:假设这一对牌在 \(x,y\) 位置,那操作完 \([1,x-1]\) 后剩余没匹配的牌需要堆在同一堆里;操作 \([x+1,y-1]\) 后没匹配的牌需要都堆在另一堆里。
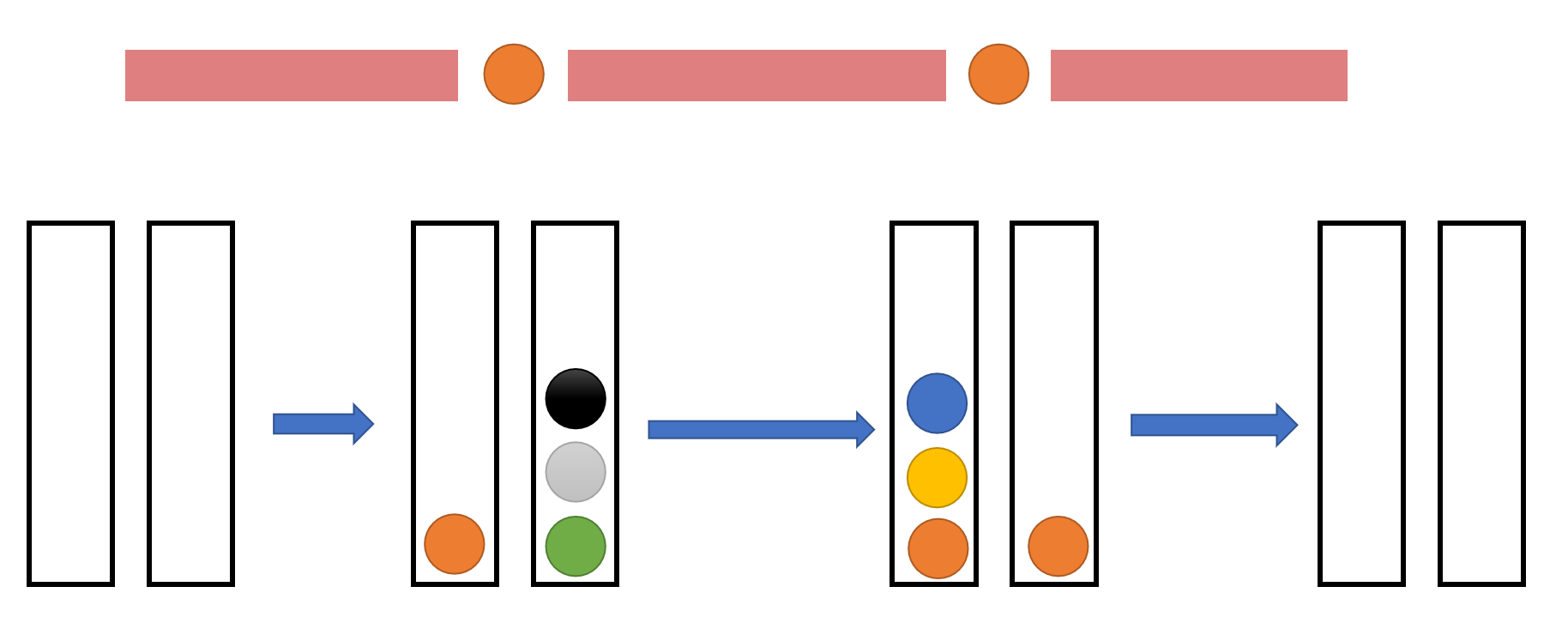
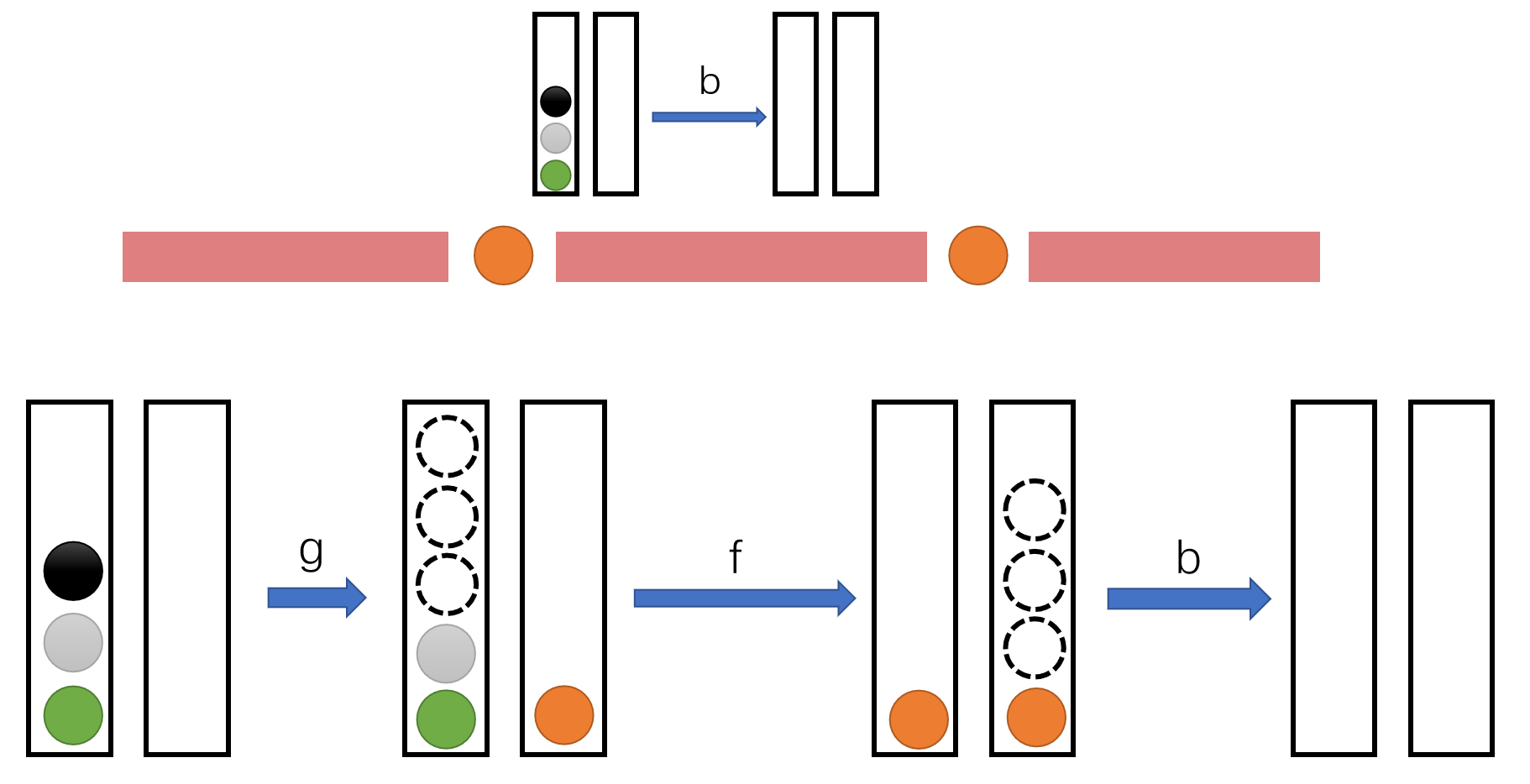
设 \(f(l,r)\) 表示:一开始,所有一个在 \([1,l-1]\) 中,一个在 \([l,r]\) 中的牌都在同一堆,进行 \([l,r]\) 的操作后,能否使这些牌清空,并且从 \([l,r]\) 中开始出现并未被消掉的牌都在另一堆。(注意到这里初始状态不需要管 一个在 \([1,l-1]\) 中,一个在 \([r+1,n]\) 中的牌 的位置,转移的时候要把这些牌当作不存在)
设 \(g(l,r)\) 表示的 初始状态和 \(f(l,r)\) 的相同,但是最后从 \([l,r]\) 中开始出现并未被消掉的牌都在同一堆。
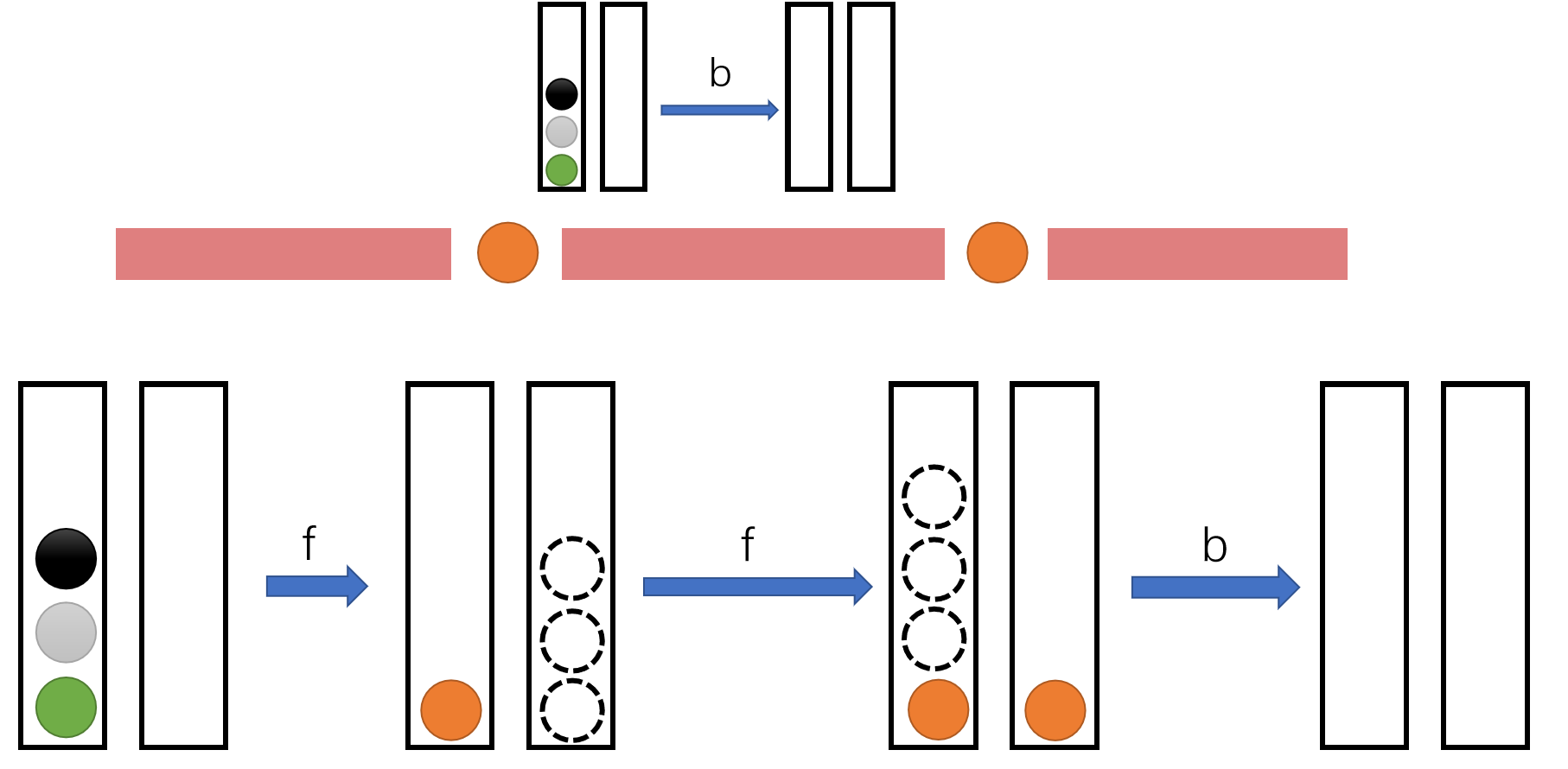
设 \(both(l,r)\) 表示 初始状态和 \(f(l,r)\) 的相同,但是操作 \([l,r]\) 消完后没有剩余的牌。
一个区间要么有 \(f/g\) 两种状态,要么有 \(both\) 一种状态。
细节好难描述,先传个官方题解的图((
\(f\):
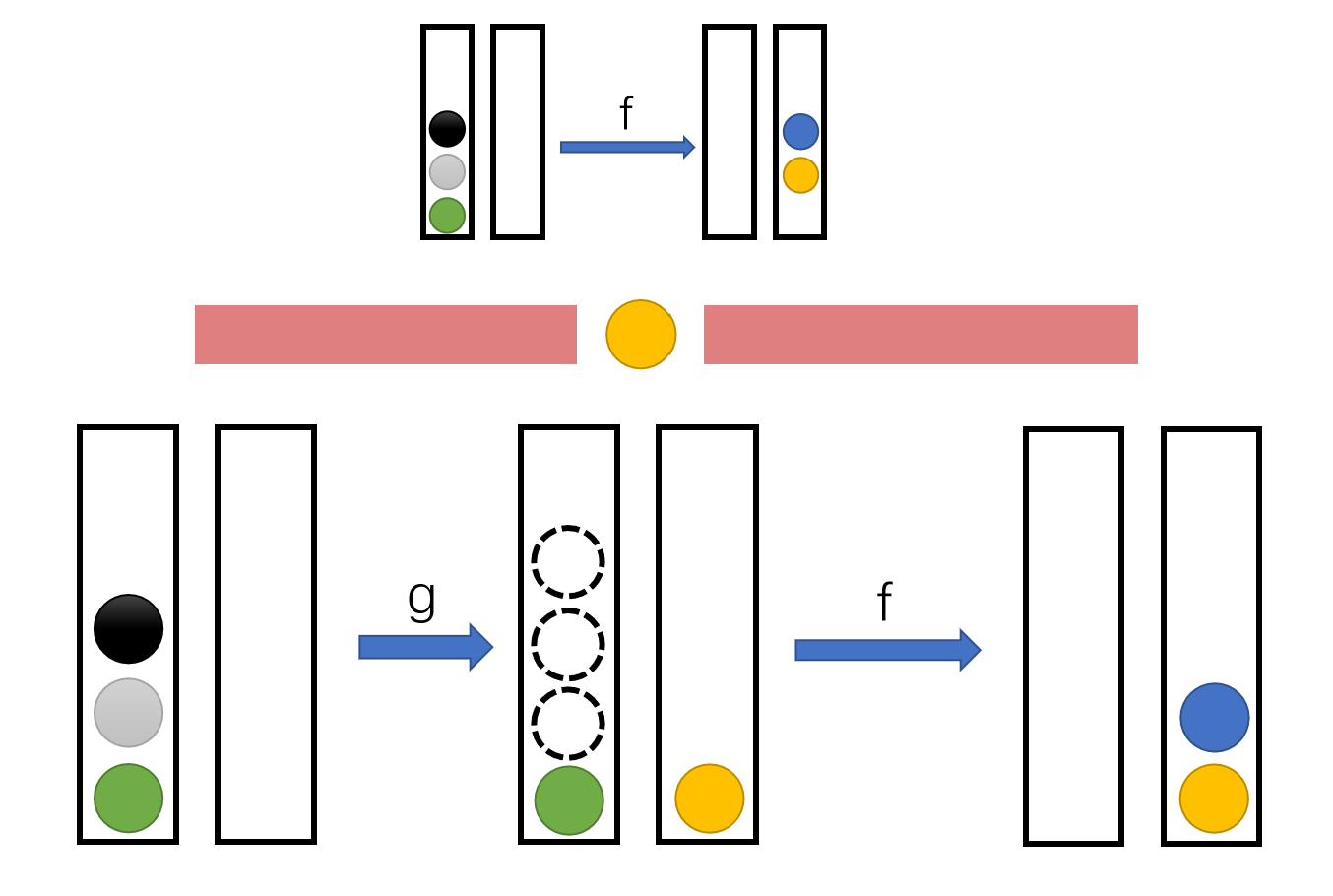
\(g\):
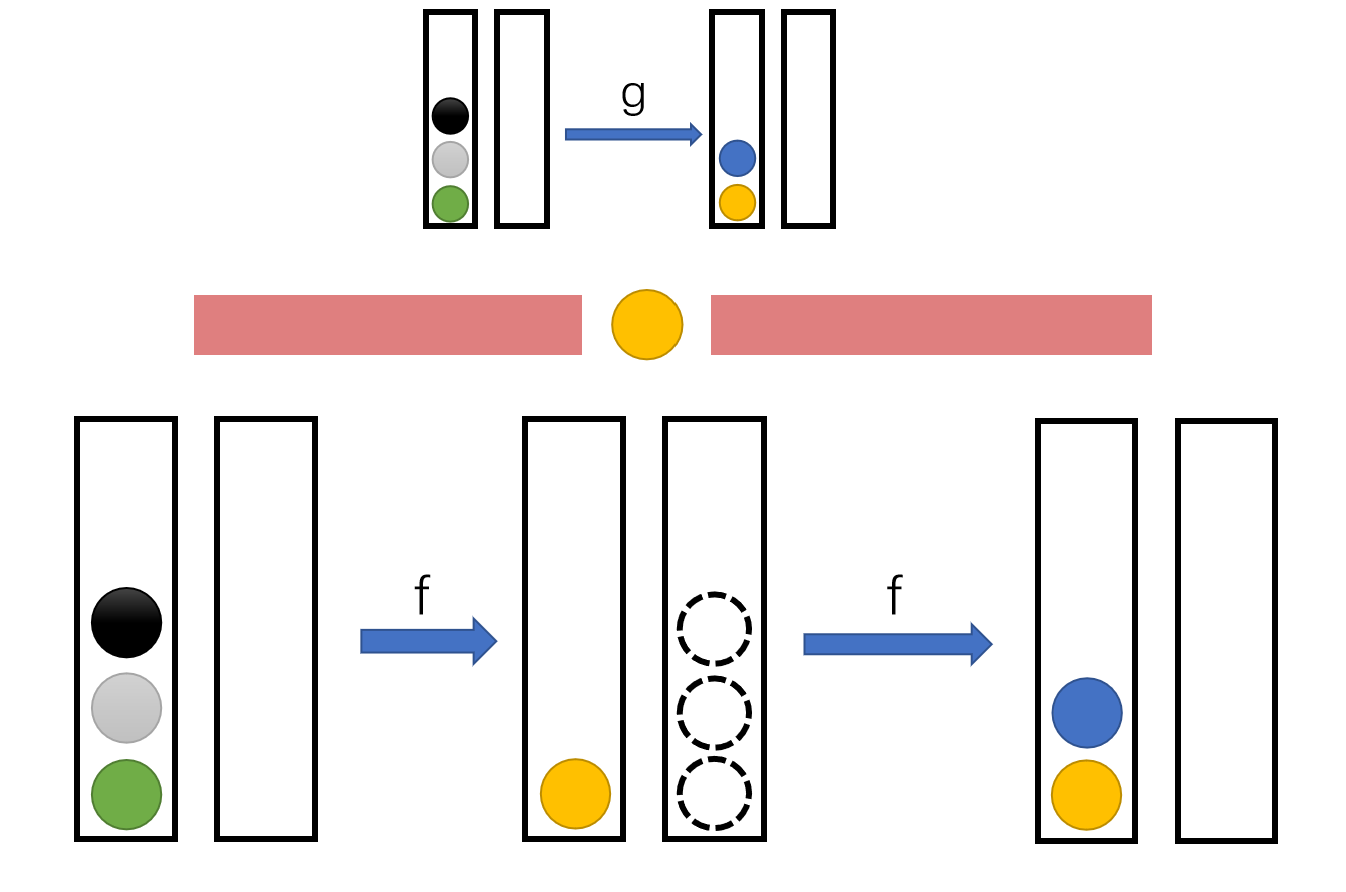
\(both\):
第一种:考虑当前在栈底的牌。
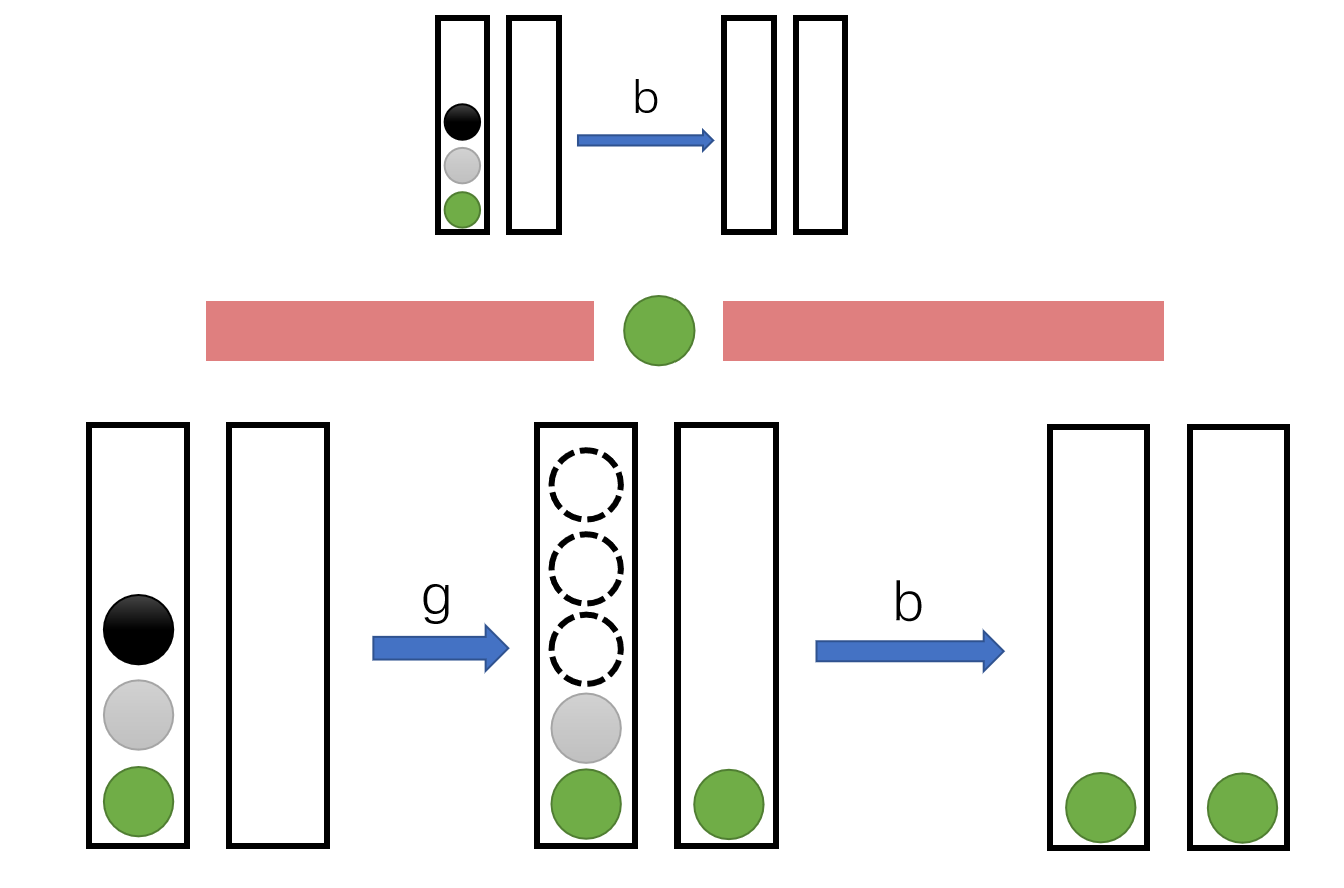
第二种 & 第三种:考虑枚举最后被消除的是哪种牌。
I
大概出题人是对着 idea 出的题,所以正着想很难。
类似强连通分量耳分解的思想。我们每次钦定从编号最小、并且没定出边的点开始(有白点则为最小的白点,否则为最小的黑点,这里钦定了标号所以不用乘系数),一路确定出边,并最终到达一个定过出边的点(新加了一条链)或形成新的连通块(新加了一个 \(ρ\) 型,一条杆一个环)。
设 \(f_{i,j}\) 表示已经扩展了若干轮,用了 \(i\) 个白点和 \(j\) 个黑点。
类似 dp 分步转移的思想,每次从当前状态新加一个点作为转移,或者结束这一轮加点(转移到 \(f\))。
设 \(g_{i,j,0/1,0/1}\) 表示正在加一条链,记录钦定链末尾的颜色以及当前点的颜色。
设 \(h_{i,j,0/1}\) 表示正在加一个 \(ρ\) 型的杆,记录当前点颜色。
设 \(l_{i,j,0/1,0/1,0/1,0/1}\) 表示正在加一个 \(ρ\) 型的环,记录环末尾的颜色,当前点颜色,环上的白点个数奇偶性,环上的黑点个数奇偶性。
然后讨论一下转移就好了。
djq 有容斥做法,zky 有生成函数的 \(n^2\log^2 P\) 做法,但是我太菜了不会

