被迫营业
鸽巢原理
利用鸽巢原理做构造:CF618F AGC025D ...
二项式定理
一些二项式的常用式子
二项式定理: \((x+y)^k=\sum\limits_{i=0}^k\dbinom{k}{i}x^iy^{k-i}\)
加法递推: \(\dbinom{n}{m}=\dbinom{n-1}{m}+\dbinom{n-1}{m-1}\)
*行求和法: $\sum\limits_{i=0}^n\dbinom{r+i}{i}=\dbinom{r+n+1}{n} $
上指标求和(也能做二维的) : \(\sum\limits_{i=0}^n\dbinom{i}{m}=\dbinom{n+1}{m+1}\)
\(\dbinom{n+m}{k}=\sum\limits_{i=0}^k\dbinom{n}{i}\dbinom{m}{k-i}\)
容斥原理
处理 \(\gcd = x\) 的式子,可以算出 \(\gcd\) 为 \(x\) 的倍数的贡献,再减去 \(\gcd =2x,3x\dots\) 的贡献。例子:CF839D 。
处理 \(\gcd = 1\) 可以莫比乌斯反演掉。例子:CF439E 。
出现 “ 恰好为 x ”的条件可以容斥,同时也是二项式反演的本质。
CF451E : 存在 \(n\) 种元素,求每种元素有 \(f_i\)
个的可重集取出 \(m\) 个元素的方案数。
解法:首先不管 \(f_i\) 的限制,可以隔板法插 \(n-1\) 块板得到答案 \(\binom{n+m-1}{n-1}\) 。考虑减掉 \(1\) 号超过的,减掉 \(2\) 号超过的... 再加上 \(1,2\) 号超过的,加上 \(1,3\) 超过的... 对每种超过的情况容斥求出答案。
卡特兰数
通项公式: \(\dfrac{\binom{2n}n}{n+1}\)
递推: \(c_n = \sum_{i = 1}^{n}c_{i - 1}\cdot c_{n - i}\) ( \(n\) 个节点的二叉树数量,[AHOI2012]树屋阶梯)
实际意义:
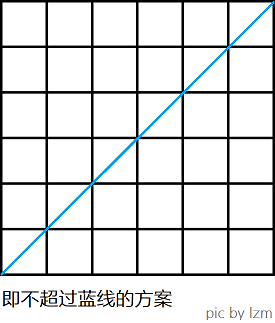
从 \((0,0)\) 到 \((n,n)\) ,每步只能向右或向上走一单位长度,不能越过第一象限角*分线的方案。
远离角*分线看做 +1 ,靠*角*分线看做 -1 ,那就是摆放 \(n\) 个 +1 , \(n\) 个 -1 ,前缀和都要 \(\ge 0\) 的方案数。(这就相当于出栈序列与括号序列)
【NOI2018】冒泡排序
打表观察,发现 \(n\) 长度的符合方案数为 \(Catalan(n)\) 。
并且有一个结论:排列符合的条件为 没有长度 \(\ge 3\) 的下降子序列。
如果前 \(i\) 个 \(\max = j\) ,第 \(i+1\) 位只能填 \(>\max\) 或小于 \(\max\) 且最小的数。
由于字典序的限制,考虑 dp 计算,并且 dp 状态要尽量便于关于字典序的统计
设 \(f(i,j)\) 为填了 \(i\) 个数,前 \(i\) 个的 \(\max = j\) ,此时填 \(i+1\sim n\) 的方案数。(为什么想到这样设?因为要让前面的符合字典序,统计后面的方案数)
对于 \(i<j\)
(填一个最小的、一个更大的)
且对于 \(i=j\) :下面没有更小的,只能填一个更大的
对于 \(i>j\) :\(f(i,j)=0\)
整合一下:
观察这个 dp 会发现 \(f(i,j)\) 的实际意义:
在网格图上 \((i,j)\to (n,n)\) ,每一轮只能向上走若干步或 0 步,然后恰好向右走一步,要求一直在第一象限角*分线上方。
如果没有字典序限制,就是从 \((0,0)\) 到 \((n,n)\) ,就是 Catalan 数。
现在要求 \(f(i,j)\) 就是 \((i,j)\to (n,n)\) 不碰到 \(y=x-1\) 的方案数,设 \((x,y)\) 为 \((i,j)\) 关于 \(y=x-1\) 的对称点,相当于 \((i,j)\to (n,n)\) 随便走的方案 减去 \((x,y)\to (n,n)\) 随便走的方案。
求出 \(f(i,j)\) 后 answer 容易计算,枚举前 \(i\) 个字典序与排列 \(p\) 相同,得出后面的方案数。
高斯消元
可以用于求解方程组,适用于有环的 DP 转移。
当矩阵中元素不为 0 的较少时,可以进行更快的高斯消元。例如: CF24D
线性代数-矩阵
三角矩阵:①上三角矩阵 它的主对角线以下(不包括主对角线)的元素均为常数 0 。②下三角矩阵 它的主对角线上方均为常数 0 。
对称矩阵:以主对角线为对称轴,各元素对应相等的矩阵。
矩阵转置:把所有矩阵中元素的横纵坐标交换,得到的矩阵,记为 \(A^T\) 。
行列式:
其中 \(P\) 为一个排列, \(\pi(P)\) 为排列逆序对数。
性质:
- \(\det(A)=\det(A^T)\)
- 交换 \(A\) 中的两行,得到 \(B\) 有 \(\det(B)=-\det(A)\)。
- 行列式中某一行的元素都 \(\times k\) ,行列式的值变为原来的 \(k\) 倍。
- 若矩阵中有两行相等,则 \(\det = 0\) ; 行列式中两行对应成比例,则 \(\det =0\) 。
- 行列式某一行乘以一个数然后加到另一行上, 行列式的值不变。
根据第五和第二条性质,可以用高斯消元讲矩阵变为对角线矩阵,对角线矩阵的行列式为对角线乘积。
线性基
对于一组向量 \(X_i\) ,\(X=\sum a_i X_i\) 得到的集合为这组向量张成的线性包。
如果存在不全为 0 的 \(a_i\) 使得 \(\sum a_i X_i = 0\) 那么就称 \(X_i\) 线性相关。
如果 \(X\) 线性相关,那么至少有一个 \(X_i\) 是其他向量的线性组合。
如果 \(V\) 是一个非零的线性包,而 \(X_i\) 线性无关且 \(X\) 张成的线性包为 \(V\) ,那么说 \(X\) 是 \(V\) 的一个基。
那么 \(V\) 中的任何元素都可以被表示为 \(\sum X_i a_i\) 。
异或线性基:对于整数的每一位看做一个维度,在集合 \(A\) 中,选出若干个数 \(X_i\) ,使得任取 \(X_i\) 异或不为 0 ,且任取 \(X_i\) 异或可以表示 \(A\) 中任何元素异或的结果,则 \(X\) 为 \(X\) 的异或线性基。
性质:(设异或线性基大小为 \(cnt\) ,集合 \(A\) 大小为 \(n\))
将集合 \(A\) 任取元素异或出的 \(2^{n}\) 个数排在一起,则有 \(2^{cnt}\) 个不同的数,且出现次数均为 \(2^{n-cnt}\) 。
线性基的插入:一位位考虑,能插入则插入,否则异或上当前有的数。
int a[32];
inline bool ins(int x){
Rep(i,31,0)
if(x>>i&1){
if(a[i])x^=a[i];
else return a[i]=x,1;
}
return 0;
}
线性基求能异或出的最大值、最小值:从高到低贪心。
inline int getmax(int x=0){
Rep(i,31,0)x=max(x,x^a[i]);
return x;
}
【清华集训2014】玛里苟斯 :线性基 + 分类讨论。
【集训队互测2015】最大异或和 :带删除线性基(保留所有的 0 环)。
图上线性基:找出图上所有的环,将 xor 插入线性基。

