基础算法——前缀和、差分 学习笔记

前缀和及差分

前缀和

一维前缀和

定义

一维前缀和，就是数组前若干项的和。

我们对于前缀和数组的定义非常广泛，

例如定义 \(S(x)\) 表示数组 \(A(x)\) 的前缀和，

定义 \(A(l,r)\) 表示 \(A(l)+A(l+1)+\dots+A(r)\)，

• \(S(x)=A(0,x)\)；

• \(S(x)=A(1,x)\)；

• \(S(x)=A(1,x-1)\)；

• \(S(x)=A(0,x-1)\)。

都是可以的，只不过我们一般用前两个。

实现

我们可以枚举每一个元素，用，

\[S(x)=\sum_{i=1}^xA(i) \]

表示前缀和，那么有递推式，

\[S(x)=S(x-1)+A(x),S(0)=0 \]

这是显然的。

C++ 语言中自带的前缀和函数为 std::partial_sum，

• 形如：partial_sum(begin, end, dist)，
• 表示 [begin, end) 的前缀和放在 dist 开始的位置，
• 返回终止迭代器。

---

• 实现 1

  最经典的方法，

  for (int i = 1; i <= n; ++i)
      S[i] = S[i - 1] + A[i];
  

  这种方法会保留原数组的内容。

• 实现 2

  我们在原数组直接进行操作，

  for (int i = 1; i <= n; ++i)
      A[i] += A[i - 1];
  

  这种方法不会保留原数组的内容，但是省空间。

• 实现 3

  冷知识，

  for (int i = 1; i < n; ++i)
      A[i + 1] += A[i];
  

  的速度要比前一个略快，因为编译器对前一个的优化是不到位的。

  这个问题在 GCC 12 修复，NOI-Linux 中的 GCC 9 是未修复的版本^[1]。

• 实现 4

  使用 STL 函数，

  partial_sum(A + 1, A + n + 1, A + 1);
  

  进行原地的前缀和。

应用

我们可以利用一维前缀和，进行不带修的 \(\mathcal O(1)\) 区间求和。

具体的，

\[S(l,r)=S(r)-S(l-1) \]

这是显然的。

另外，修改复杂度为 \(\mathcal O(n)\)，一般不会使用。

如果要修改，一般会配合概率相关，

如果进行 \(m\) 次操作，每次操作修改的概率是 \(1/n\)，

那么就可以进行 \(\mathcal O(n)\) 的修改，因为这样均摊的复杂度依旧是 \(\mathcal O(m)\) 的。

二维前缀和

定义

我们直接取比较常见的定义，

\[S(x,y)=\sum_{i\le x}\sum_{j\le y}A(i,j) \]

几何意义就是，将二维平面划分为网格，建立平面直角坐标系。

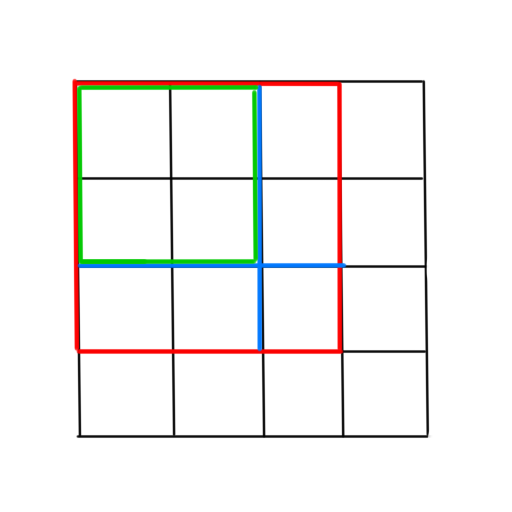
那么，其前缀和平面的每一个点表示的就是，

从原点（此处是 \((1,1)\)）到这个点的矩形的权值和。

实现

那么可以容斥解决，

\[S(x,y)=A(x,y)+S(x-1,y)+S(x,y-1)-S(x-1,y-1) \]

这么做是最直观的。

应用

不带修子区间求和问题，具体的，

\[S(a,b,c,d)=S(c,d)-S(c,b-1)-S(a-1,d)+S(a-1,b-1) \]

同样修改复杂度是 \(\mathcal O(n^2)\) 的重构。

高维前缀和

定义

代数表示为，

\[S(x_1,x_2\dots,x_k)=\sum_{i_1\le x_2}\sum_{i_2\le x_2}\dots\sum_{i_k\le x_k}A(i_1,i_2,\dots,i_k) \]

一般只有三维前缀和是具有直观的几何意义的，但是我们也不去讨论。

实现

假设我们要求边长为 \(n\) 的 \(k\) 维超正方体的前缀和，

那么，如果继续使用容斥原理，复杂度将是 \(\mathcal O(n^k2^k)\) 的，也就是说项数为 \(2^k\) 的。

这显然是难以接受的（在 \(3\) 维中就有 \(8\) 项，这是很恐怖的）。

但是，我们有一个类似 DP 的求解高维前缀和的方法，我们下面仅以 \(3\) 维为例。

我们先枚举每一个维度，然后对这个维度下进行前缀和，那么复杂度就是 \(\mathcal O(n^kk)\) 的。

尽管这个复杂度依然很大，但是一般来说我们很少讨论 \(4\) 维以上的前缀和，因此还是凑合的。

板子题：AtCoder - abc366_d - Cuboid Sum Query。

// 读入
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
    for (int k = 1; k <= n; ++k)
	cin >> s[i][j][k];
// 将第一维前缀和
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
    for (int k = 1; k <= n; ++k)
	s[i][j][k] += s[i - 1][j][k];
// 将第二维前缀和
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
    for (int k = 1; k <= n; ++k)
	s[i][j][k] += s[i][j - 1][k];
// 将第三维前缀和
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
    for (int k = 1; k <= n; ++k)
	s[i][j][k] += s[i][j][k - 1];

应用

高维子超立方体求和，我们发现式子会很复杂，

于是我们依然类似 DP 的，将每一个维度拆分考虑。

依旧以上一题的三维为例，我们使用 C++ 的函数重载特性，

int query(int x, int y, int z) {
    return s[x][y][z];
}

// 拆分第三维
int query(int x, int y, int lz, int rz) {
    return query(x, y, rz) - query(x, y, lz - 1);
}

// 拆分第二维
int query(int x, int ly, int ry, int lz, int rz) {
    return query(x, ry, lz, rz) - query(x, ly - 1, lz, rz);
}

// 拆分第一维
int query(int lx, int rx, int ly, int ry, int lz, int rz) {
    return query(rx, ly, ry, lz, rz) - query(lx - 1, ly, ry, lz, rz);
}

这就比较好理解了。

差分

一维差分

定义

我们定义 \(D\) 为 \(A\) 的差分，即，

\[D(x)=A(x)-A(x-1) \]

对于一个长度为 \(n\) 的序列 \(A[1,n]\)，有，

\[D(x)=\begin{cases} A(x)-A(x-1)&x\in[2,n]\\ A(x)&x=1 \end{cases} \]

性质：

• 数组 \(A\) 的前缀和 \(S\) 的差分是 \(A\)；

• 数组 \(A\) 的差分 \(D\) 的前缀和是 \(A\)。

即，差分与前缀和互为逆运算。

• 构造性的理解：

  我们构造差分数组的过程，也可以构造性的来看：

  我们知道数组 \(A\)，求一个数组 \(D\) 使得 \(D\) 的前缀和是 \(A\)。

  考虑 \(A(x)\) 的所有贡献，发现我们进行前缀和的时候就会对它及其后面所有数造成贡献。

  因此，我们对于 \(A(x)\)，进行操作，

  \[\begin{aligned} D(x)&\gets D(x)+A(x)\\ D(x+1)&\gets D(x+1)-A(x) \end{aligned} \]

  那么进行前缀和的时候就会消去多余的贡献了。

  然后再反过来考虑每一个 \(D(x)\) 受到了什么贡献，容易发现就是，

  \[D(x)=A(x)-A(x-1) \]

  这就是一种构造性的理解。

C++ 中也有差分的函数 std::adjacent_difference，

• 形如：adjacent_difference(begin, end, dist)，
• 表示 [begin, end) 对相邻两项的差值，
• 放在 dist + 1 开始的位置，返回终止迭代器。

应用

类似上文构造性的方法，我们可以利用差分数组，进行 \(\mathcal O(1)\) 的区间加，\(\mathcal O(n)\) 的单点查询：

• 对 \([l,r]\) 加上 \(x\)：令 \(D(l)\gets D(l)+x,D(r+1)\gets D(r+1)-x\)；

• 查询：对数组跑一遍前缀和，发现多余的贡献都被消除了，那么就可以直接访问。

二维差分

定义

我们可以直接定义 \(D\) 为 \(A\) 的二维差分，当且仅当 \(D\) 的二维前缀和为 \(A\)。

考虑构造，我们发现只需要令，

\[\begin{aligned} D(x,y)&\gets D(x,y)+A(x,y)\\ D(x+1,y)&\gets D(x+1,y)-A(x,y)\\ D(x,y+1)&\gets D(x,y+1)-A(x,y)\\ D(x+1,y+1)&\gets D(x+1,y+1)+A(x,y) \end{aligned} \]

这样子就是正确的。

应用

类似一维，可以进行 \(\mathcal O(1)\) 的子矩阵加，\(\mathcal O(n^2)\) 的单点查询。

具体略。

树上问题

一般讨论点权和边权。

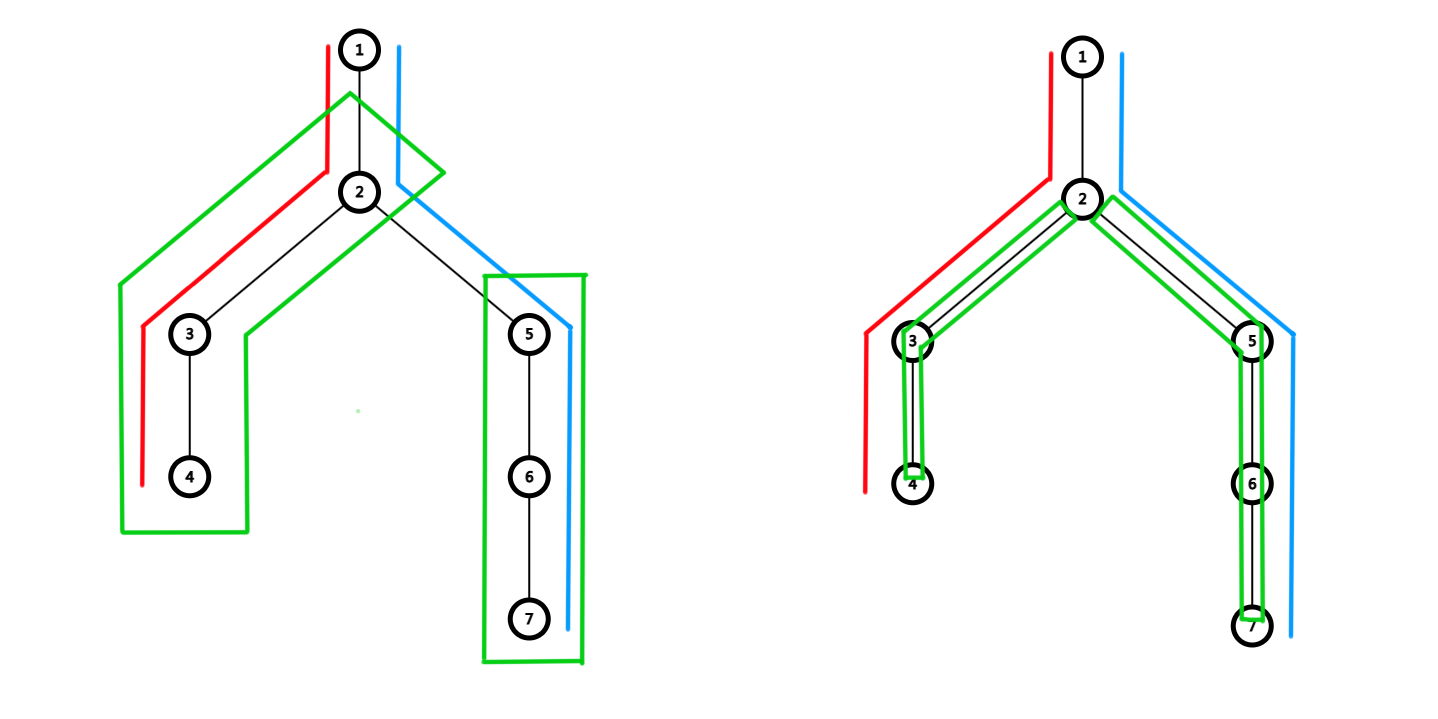
对于边权通常比较难处理，会下方到点权，下文所说边权均为下放到点权后的。

树上前缀和

设 \(S(u)\) 表示从根到节点 \(u\) 经过的所有权值和。

设 \(S(x,y)\) 表示 \(x\to y\) 路径上的权值和，

• 若是点权，\(S(x,y)=S(x)+S(y)-S(\mathrm{LCA})-S(\mathrm{fa_{LCA}})\)；

• 若是边权，\(S(x,y)=S(x)+S(y)-2S(\mathrm{LCA})\)。

树上差分

树上差分可以用于在树上快速修改然后统一查询。

一般我们会对一条链进行操作，假设我们对 \(x\to y\) 路径上的权值进行修改，

• 若是点权，我们对 \(x,y\) 加 \(1\) 倍，对 \(\mathrm{LCA}\) 减 \(1\) 倍，对 \(\mathrm{fa_{LCA}}\) 减 \(1\) 倍即可。

• 若是边权，我们对 \(x,y\) 加 \(1\) 倍，对 \(\mathrm{LCA}\) 减 \(2\) 倍即可。

其他前缀

前缀积

我们设，

\[P(x)=\prod_{i=1}^xA(i) \]

前缀积一般是满足可差分性的，但是取模后就不一定了。

例如，在某一处的前缀积关于模数不存在乘法逆元的情况。

我们只讨论满足可差分性的，那么有，

\[P(l,r)=\frac{P(r)}{P(l-1)} \]

特殊的，我们定义 \(P(0)=1\)。

可以用于求一段区间的乘积，但是不常用，因为乘大了自然需要取模。

前缀最大最小值

以最大值为例。

我们设，

\[M(x)=\max_{i=1}^xA(i) \]

这显然不满足可差分性，因此不能求区间的结果。

但是依然应用很广泛。

前缀异或和

我们设，

\[R(x)=\bigoplus_{i=1}^xA(i) \]

其中 \(\oplus\) 运算符表示按位异或 \(\operatorname{xor}\) 运算。

注意到这是满足可差分性的，因为 \(x\operatorname{xor}x=0\)，因此，

\[R(l,r)=R(r)\bigoplus R(l-1) \]

这个也存在应用。

还有一些好玩的详见异或哈希算法。

---

1. 参考 2024 国家集训队论文 宋佳兴《论现代硬件上的常数优化》。 ↩︎