数据结构——数列分块学习笔记

下面部分代码使用，

using ll = long long;
#define int ll

基础思想

问题引入

问题：实现

区间加；
区间求和。

基本结构

引用经典东西，

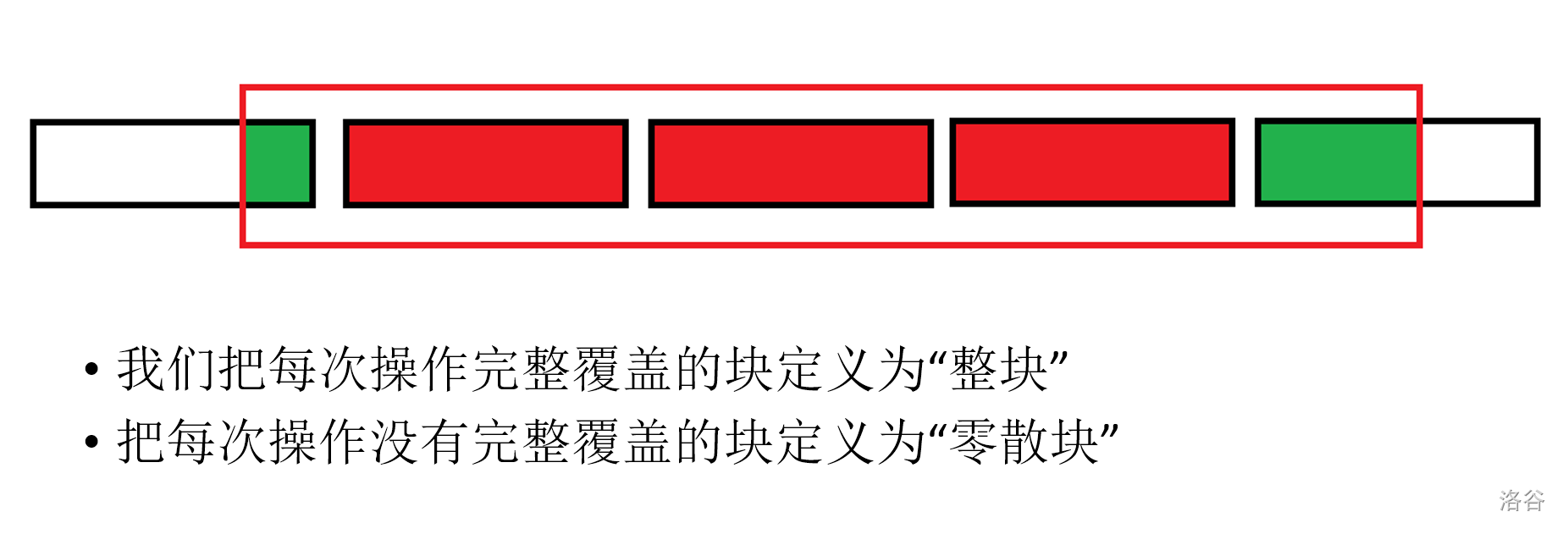
我们考虑构造一个结构，形如，

那么，结论是，

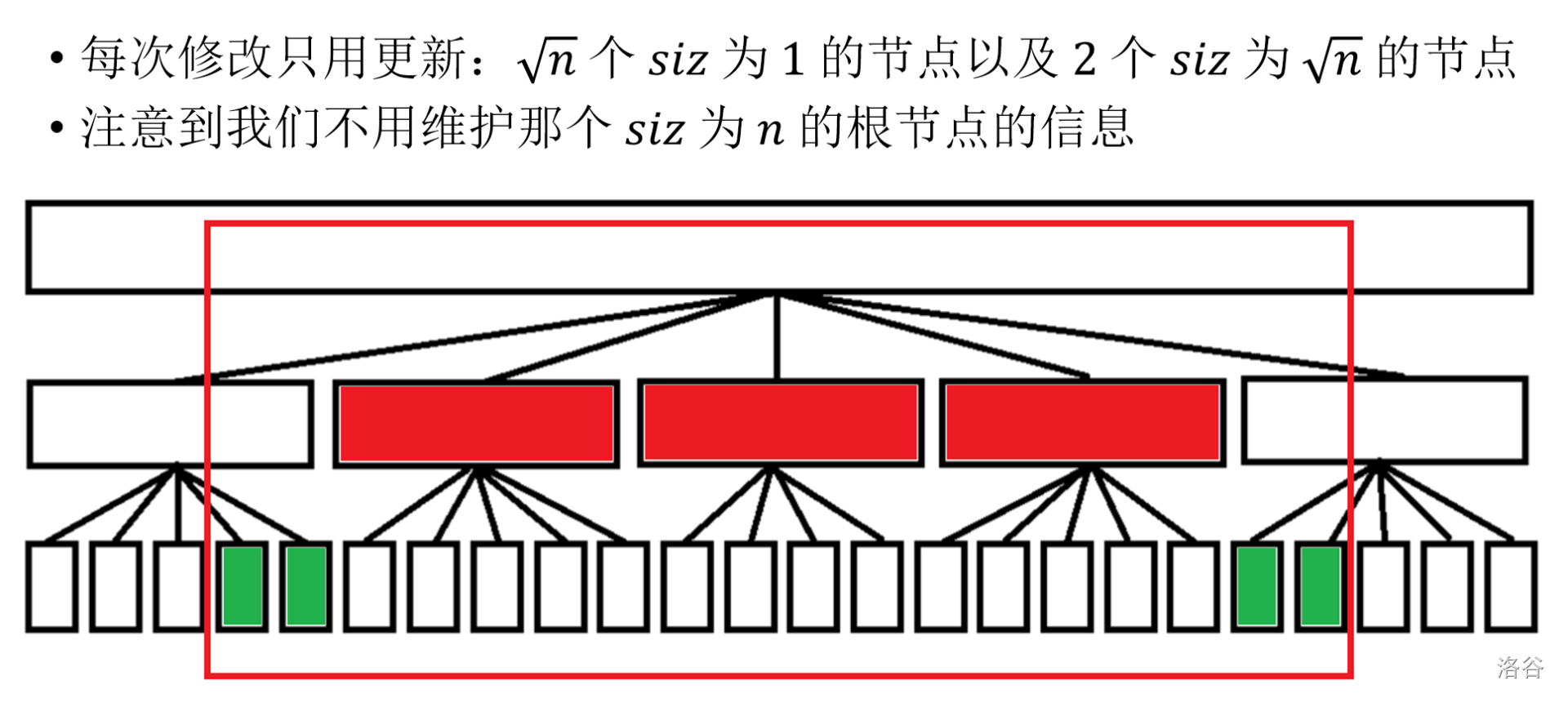
复杂度证明

为什么块长一般是 \(\sqrt n\) 呢？

我们假设构造的块长是 \(B\)，那么总块数为，

\[{n\over B} \]

我们每一次修改查询，复杂度，

在一块内，暴力枚举，\(\mathcal O(B)\)；
不在一块内，枚举整块、零散块，\(\mathcal O(n/B+B)\)。

根据均值不等式，

\[{n\over B}+B\ge2\sqrt n \]

取等当且仅当 \(b=\sqrt n\)。

分块的应用

如果在分治结构上很难快速合并某些信息，我们就可以利用分块来做。

简化实现

上面的问题，区间加，区间求和。

预处理

int n, siz, cnt;
int a[N], tag[N];
int belong[N], L[N], R[N];

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
		belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
		L[i] = (i - 1) * siz + 1,
		R[i] = L[i] + siz - 1;
	R[cnt] = n;
}

n 表示原数组（a）长度；
siz 表示块长；
cnt 表示总块数；
belong[i] 表示原数组第 \(i\) 个被分到了第几块；
tag[i] 表示第 \(i\) 块上面的附加值；
L[i],R[i] 分别表示第 \(i\) 块的左、右端点。

特判在同一块内的情况，处理左右零散块和各个整块。

1 区间加、单点查询

不维护整块信息（单点查询）：

constexpr int N = 5e4 + 10;

int n, siz, cnt;
int belong[N], L[N], R[N];
int a[N], tag[N];

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
		belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
		L[i] = (i - 1) * siz + 1,
		R[i] = L[i] + siz - 1;
	R[cnt] = n;
}

void add(int l, int r, int c) {
	int p = belong[l], q = belong[r];
	if (p == q) {
		for (int i = l; i <= r; ++i) a[i] += c;
		return;
	}
	for (int i = l; i <= R[p]; ++i) a[i] += c;
	for (int i = p + 1; i <= q - 1; ++i) tag[i] += c;
	for (int i = L[q]; i <= r; ++i) a[i] += c;
}

signed main() {
	cin >> n; build();
	for (int i = 1; i <= n; ++i) cin >> a[i];
	for (int i = 1; i <= n; ++i) {
		int op, l, r, c;
		cin >> op >> l >> r >> c;
		if (op == 0) add(l, r, c);
		else cout << a[r] + tag[belong[r]] << endl;
	}
	return 0;
}

4 区间加、区间查询

constexpr int N = 5e4 + 10;

int n, siz, cnt;
int belong[N], L[N], R[N];
ll a[N], sum[N], tag[N];

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
		belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
		L[i] = (i - 1) * siz + 1,
		R[i] = L[i] + siz - 1;
	R[cnt] = n;
}

void add(int l, int r, int c) {
	int p = belong[l], q = belong[r];
	if (p == q) {
		for (int i = l; i <= r; ++i)
			a[i] += c, sum[p] += c;
		return;
	}
	for (int i = l; i <= R[p]; ++i)
		a[i] += c, sum[p] += c;
	for (int i = p + 1; i <= q - 1; ++i)
		sum[i] += c * (R[i] - L[i] + 1), tag[i] += c;
	for (int i = L[q]; i <= r; ++i)
		a[i] += c, sum[q] += c;
}

ll query(int l, int r, int m) {
	int p = belong[l], q = belong[r];
	ll res = 0;
	if (p == q) {
		for (int i = l; i <= r; ++i)
			res = (res + a[i] + tag[p]) % m;
		return res;
	}
	for (int i = l; i <= R[p]; ++i)
		res = (res + a[i] + tag[p]) % m;
	for (int i = p + 1; i <= q - 1; ++i)
		res = (res + sum[i]) % m;
	for (int i = L[q]; i <= r; ++i)
		res = (res + a[i] + tag[q]) % m;
	return res;
}

signed main() {
	cin >> n; build();
	for (int i = 1; i <= n; ++i)
		cin >> a[i], sum[belong[i]] += a[i];
	for (int i = 1; i <= n; ++i) {
		int op, l, r, c;
		cin >> op >> l >> r >> c;
		if (op == 0) add(l, r, c);
		else cout << query(l, r, c + 1) << endl;
	}
	return 0;
}

特判在同一块内的情况，处理左右零散块和各个整块。

6 单点插入、单点查询

使用 STL rope。

#include <bits/stdc++.h>
#include <ext/rope>

using namespace std;
using namespace __gnu_cxx;

int n;

rope<int> a;

signed main() {
	cin >> n; a.push_back(0);
	for (int i = 1, x; i <= n; ++i)
		cin >> x, a.push_back(x);
	for (int i = 1; i <= n; ++i) {
		int op, l, r, c;
		cin >> op >> l >> r >> c;
		if (op == 0) a.insert(l, r);
		else cout << a[r] << endl;
	}
	return 0;
}

第零部分：

构造函数	解释
`rope<T>`	构造一个类型为 `T` 的数组
`crope`	等同于 `rope<char>`
`rope<T>(siz)`	构造一个长度为 `siz` 的数组
`rope<T>(siz, val)`	构造一个长度为 `siz` 的初始值均为 `val` 的数组

第一部分：

操作	解释
`a[p]` 或 `a.at(p)`	返回 `p` 处的元素（只读）
`a.size()`	返回大小
`a.empty()`	返回是否为空
`a.clear()`	清空（删除所有元素）
`a.begin()` / `a.end()`	迭代器
`a.rbegin()` / `a.rend()`	反向迭代器
`a.front()` / `a.back()`	返回首位元素
`a.c_str()`	返回 c 风格数组（只读）

第二部分：

操作	解释
`a.push_back(x)`	在末尾添加 `x` 元素
`a.pop_back()`	在某位删除
`a.push_front(x)`	在开头添加 `x` 元素
`a.pop_front()`	在开头删除

第三部分：

操作	解释
`a.insert(p, x)`	在下标 `p` 前插入 `x` 元素
`a.insert(p, c, x)`	在下标 `p` 前插入 `c` 个 `x` 元素
`a.erase(p)`	从下标 `p` 开始删除 \(1\) 个元素
`a.erase(p, c)`	从下标 `p` 开始删除 `c` 个元素
`a.replace(p, x)`	把下标 `p` 处的元素替换为 `x` 元素
`a.substr(p, x)`	从下标 `p` 开始截取 `x` 个返回

数列分块入门九题

2 区间加，区间排名

区间加；
区间查小于某个数的数量。

constexpr int N = 5e4 + 10;

int n, siz, cnt;
int belong[N], L[N], R[N];
int a[N], tag[N];
int sorted[N], is[N];

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
		belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
		L[i] = (i - 1) * siz + 1, R[i] = L[i] + siz - 1;
	R[cnt] = n;
}

void add(int l, int r, int c) {
	int p = belong[l], q = belong[r];
	if (p == q) {
		for (int i = l; i <= r; ++i) a[i] += c;
		return void(is[p] = 0);
	}
	for (int i = l; i <= R[p]; ++i)
		a[i] += c;
	is[p] = 0;
	for (int i = p + 1; i <= q - 1; ++i)
		tag[i] += c;
	for (int i = L[q]; i <= r; ++i)
		a[i] += c;
	is[q] = 0;
}

int query(int l, int r, ll c) {
	int p = belong[l], q = belong[r];
	int res = 0;
	if (p == q) {
		for (int i = l; i <= r; ++i)
			res += (a[i] + tag[p]) < c;
		return res;
	}
	for (int i = l; i <= R[p]; ++i)
		res += (a[i] + tag[p]) < c;
	for (int i = p + 1; i <= q - 1; ++i) {
		if (!is[i])
			copy_n(a + L[i], siz, sorted + L[i]),
			sort(sorted + L[i], sorted + R[i] + 1), is[i] = 1;
		res += lower_bound(sorted + L[i], sorted + R[i] + 1, c - tag[i]) - (sorted + L[i]);
	}
	for (int i = L[q]; i <= r; ++i)
		res += (a[i] + tag[q]) < c;
	return res;
}

signed main() {
	cin >> n; build();
	for (int i = 1; i <= n; ++i)
		cin >> a[i], sorted[i] = a[i];
	for (int i = 1; i <= cnt; ++i)
		sort(sorted + L[i], sorted + R[i] + 1), is[i] = 1;
	for (int i = 1; i <= n; ++i) {
		int op, l, r, c;
		cin >> op >> l >> r >> c;
		if (op == 0) add(l, r, c);
		else cout << query(l, r, 1ll * c * c) << endl;
	}
	return 0;
}

a 表示原数组；
tag 表示区间加标记；
sorted 表示分块后块内排序的结果；
is 表示一个块是否排序完。

3 区间加，区间前驱

和上一题类似，

int query(int l, int r, int c) {
	int p = belong[l], q = belong[r];
	int res = INT_MIN, flag = 0;
	if (p == q) {
		for (int i = l; i <= r; ++i)
			if (a[i] + tag[p] < c)
				flag = 1, res = max(res, a[i] + tag[p]);
		return flag ? res : -1;
	}
	for (int i = l; i <= R[p]; ++i)
		if (a[i] + tag[p] < c)
			flag = 1, res = max(res, a[i] + tag[p]);
	for (int i = p + 1; i <= q - 1; ++i) {
		if (!is[i])
			copy_n(a + L[i], siz, sorted + L[i]),
			sort(sorted + L[i], sorted + R[i] + 1), is[i] = 1;
		auto it = lower_bound(sorted + L[i], sorted + R[i] + 1, c - tag[i]) - 1;
		if (*it + tag[i] < c)
			flag = 1, res = max(res, *it + tag[i]);
	}
	for (int i = L[q]; i <= r; ++i)
		if (a[i] + tag[q] < c)
			flag = 1, res = max(res, a[i] + tag[q]);
	return flag ? res : -1;
}

signed main() {
	cin >> n; build();
	for (int i = 1; i <= n; ++i)
		cin >> a[i], sorted[i] = a[i];
	for (int i = 1; i <= cnt; ++i)
		sort(sorted + L[i], sorted + R[i] + 1), is[i] = 1;
	for (int i = 1; i <= n; ++i) {
		int op, l, r, c;
		cin >> op >> l >> r >> c;
		if (op == 0) add(l, r, c);
		else cout << query(l, r, c) << endl;
	}
	return 0;
}

5 区间开方，区间查询

注意到，开方一定次数以后，所有的数都会在 \(0,1\) 不变。

即 \(f(x)=\sqrt x\) 在正数的不动点为 \(0,1\)，因此，

维护 tag 表示一个段是否已经变为了 \(0,1\)；
如果一个段已经变成了 \(0,1\) 那么就不需要再开方了。

洛谷上的题是：P4145 上帝造题的七分钟 2 / 花神游历各国。

constexpr int N = 5e4 + 10;

int n, siz, cnt;
int belong[N], L[N], R[N];
int a[N], sum[N], tag[N];
// tag: is 0 or 1

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
		belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
		L[i] = (i - 1) * siz + 1, R[i] = L[i] + siz - 1;
	R[cnt] = n;
}

void m_sqrt(int l, int r) {
	int p = belong[l], q = belong[r];
	if (p == q) {
		if (tag[p]) return;
		for (int i = l; i <= r; ++i) {
			sum[p] -= a[i];
			a[i] = sqrt(a[i]);
			sum[p] += a[i];
		}
		return;
	}
	if (!tag[p])
		for (int i = l; i <= R[p]; ++i) {
			sum[p] -= a[i];
			a[i] = sqrt(a[i]);
			sum[p] += a[i];
		}
	for (int i = p + 1; i <= q - 1; ++i) {
		if (tag[i]) continue;
		int fl = true; sum[i] = 0;
		for (int j = L[i]; j <= R[i]; ++j) {
			a[j] = sqrt(a[j]), sum[i] += a[j];
			if (a[j] > 1) fl = false;
		}
		tag[i] = fl;
	}
	if (!tag[q])
		for (int i = L[q]; i <= r; ++i) {
			sum[q] -= a[i];
			a[i] = sqrt(a[i]);
			sum[q] += a[i];
		}
}

int query(int l, int r) {
	int p = belong[l], q = belong[r];
	int res = 0;
	if (p == q) {
		for (int i = l; i <= r; ++i) res += a[i];
		return res;
	}
	for (int i = l; i <= R[p]; ++i) res += a[i];
	for (int i = p + 1; i <= q - 1; ++i) res += sum[i];
	for (int i = L[q]; i <= r; ++i) res += a[i];
	return res;
}

signed main() {
	cin >> n; build();
	for (int i = 1; i <= n; ++i)
		cin >> a[i], sum[belong[i]] += a[i];
	for (int i = 1; i <= n; ++i) {
		int op, l, r, c;
		cin >> op >> l >> r >> c;
		if (op == 0) m_sqrt(l, r);
		else cout << query(l, r) << endl;
	}
	return 0;
}

7 区间加乘，单点查询

类似线段树 2 的 tag 处理即可。

constexpr int N = 1e5 + 10;

constexpr int MOD = 10007;

int n, siz, cnt;
int belong[N], L[N], R[N];
int a[N], tagadd[N], tagmul[N];

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
		belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
		L[i] = (i - 1) * siz + 1, R[i] = L[i] + siz - 1,
		tagadd[i] = 0, tagmul[i] = 1;
	R[cnt] = n; 
}

void rebuild(int x) {
	for (int i = L[x]; i <= R[x]; ++i)
		a[i] = (a[i] * tagmul[x] % MOD + tagadd[x]) % MOD;
	tagadd[x] = 0, tagmul[x] = 1;
}

void modify(int l, int r, int mul, int add) {
	int p = belong[l], q = belong[r];
	if (p == q) {
		rebuild(p);
		for (int i = l; i <= r; ++i)
			a[i] = (a[i] * mul % MOD + add) % MOD;
		return;
	}
	rebuild(p);
	for (int i = l; i <= R[p]; ++i)
		a[i] = (a[i] * mul % MOD + add) % MOD;
	for (int i = p + 1; i <= q - 1; ++i) {
		tagmul[i] = tagmul[i] * mul % MOD;
		tagadd[i] = (tagadd[i] * mul % MOD + add) % MOD;
	}
	rebuild(q);
	for (int i = L[q]; i <= r; ++i)
		a[i] = (a[i] * mul % MOD + add) % MOD;
}

int query(int x) {
	return (a[x] * tagmul[belong[x]] % MOD + tagadd[belong[x]]) % MOD;
}

signed main() {
	cin >> n; build();
	copy_n(istream_iterator<int>(cin), n, a + 1);
	for (int i = 1; i <= n; ++i) {
		int op, l, r, c;
		cin >> op >> l >> r >> c;
		if (op == 0) modify(l, r, 1, c);
		if (op == 1) modify(l, r, c, 0);
		if (op == 2) cout << query(r) << endl;
	}
	return 0;
}

8 区间计数，区间覆盖

哈哈哈，珂朵莉，启动！

namespace odt {
	struct emm {
		int l, r;
		mutable int v;
		emm(int l): l(l) {}
		emm(int l, int r, int v): l(l), r(r), v(v) {}
		int len() const { return r - l + 1; }
		friend bool operator <(const emm &a, const emm &b) { return a.l < b.l; }
	};
	
	set<emm> cute;
	
	auto split(int x) {
		auto it = --cute.upper_bound(emm(x));
		if (it->l == x) return it;
		auto t = *it; cute.erase(it);
		cute.emplace(emm(t.l, x - 1, t.v));
		return cute.emplace(emm(x, t.r, t.v)).first;
	}
	
	auto get(int l, int r) {
		auto itr = split(r + 1), itl = split(l);
		return make_pair(itl, itr);
	}
	
	int assign(int l, int r, int v) {
		auto it = get(l, r);
		auto itl = it.first, itr = it.second;
		int res = 0;
		for (; itl != itr; ++itl)
			if (itl->v == v) res += itl->len();
		cute.erase(it.first, itr);
		cute.emplace(l, r, v);
		return res;
	}
}

signed main() {
	int n; cin >> n;
	for (int i = 1, x; i <= n; ++i)
		cin >> x, odt::cute.emplace(i, i, x);
	for (int k = 1; k <= n; ++k) {
		int l, r, c;
		cin >> l >> r >> c;
		cout << odt::assign(l, r, c) << endl;
	}
	return 0;
}

9 区间最小众数

P4168 [Violet] 蒲公英

记集合 \(S\) 的众数为 \(\text{mode}(S)\)，

根据一些性质，

\[\text{mode}(a\cup b)\in\text{mode}(a)\cup b \]

证明：若 \(t\) 既不是 \(\text{mode}(a)\) 也不属于 \(b\)，那么 \(t\) 的出现次数一定小于 \(\text{mode}(a)\)。

先离散化，块长为 \(\sqrt n\) 分块，

设 \(\text{between}(i,j)\) 表示第 \([i,j]\) 块的最小众数。
设 \(\text{prefix}(i,x)\) 表示前 \(i\) 块，数字 \(j\) 的出现次数。

那么，区间 \([l,r]\) 最小众数一定是整块的最小众数，或者散块的。

直接处理即可。

如何预处理 \(\text{prefix}\)？普及组重造。
如何预处理 \(\text{between}\)？再根据性质，加入 \(j\) 集合即可。

时间复杂度：\(\mathcal O(q\sqrt n)\)。

注意一定要加入所有的数字以后再统计；
注意算散块的时候要加上整块的次数。

constexpr int N = 1e5 + 10;
constexpr int SN = 400;

int n, a[N], siz, cnt;
int belong[N], L[N], R[N];
int between[SN][SN], prefix[SN][N];

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
        belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
        L[i] = (i - 1) * siz + 1, R[i] = L[i] + siz - 1;
	R[cnt] = n;
	for (int i = 1; i <= cnt; ++i) {
		copy_n(prefix[i - 1], n, prefix[i]);
		for (int j = L[i]; j <= R[i]; ++j) ++prefix[i][a[j]];
	}
	for (int i = 1; i <= cnt; ++i)
		for (int j = i; j <= cnt; ++j) {
			int r = between[i][j - 1];
			for (int k = L[j]; k <= R[j]; ++k) {
				int c = a[k];
                int ori = prefix[j][r] - prefix[i - 1][r];
                int now = prefix[j][c] - prefix[i - 1][c];
				if (now > ori || (now == ori && c < r)) r = c;
			}
			between[i][j] = r;
		}
}

array<int, N> bucket;

int query(int l, int r) {
    fill_n(bucket.begin(), n, 0);
	int p = belong[l], q = belong[r];
	int id = 0;
	if (q - p == 1) {
		for (int i = l; i <= r; ++i) ++bucket[a[i]];
		for (int i = l; i <= r; ++i) {
			int c = a[i];
            int ori = bucket[id];
            int now = bucket[c];
            if (now > ori || (now == ori && c < id)) id = c;
        }
		return id;
	}
	id = between[p + 1][q - 1];
	for (int i = l; i <= R[p]; ++i) ++bucket[a[i]];
	for (int i = L[q]; i <= r; ++i) ++bucket[a[i]];
    for (int i = l; i <= R[p]; ++i) {
        int c = a[i];
        int ori = bucket[id] + prefix[q - 1][id] - prefix[p][id];
        int now = bucket[c] + prefix[q - 1][c] - prefix[p][c];
        if (now > ori || (now == ori && c < id)) id = c;
    }
	for (int i = q[L]; i <= r; ++i) {
        int c = a[i];
        int ori = bucket[id] + prefix[q - 1][id] - prefix[p][id];
        int now = bucket[c] + prefix[q - 1][c] - prefix[p][c];
        if (now > ori || (now == ori && c < id)) id = c;
    }
	return id;
}

signed main() {
	cin >> n; vector<int> s(n);
	for (int i = 1; i <= n; ++i) cin >> a[i], s[i - 1] = a[i];
	sort(s.begin(), s.end()), s.erase(unique(s.begin(), s.end()), s.end());
	for (int i = 1; i <= n; ++i) a[i] = lower_bound(s.begin(), s.end(), a[i]) - s.begin();
	build();
	for (int i = 1; i <= n; ++i) {
		int l, r; cin >> l >> r;
		cout << s[query(l, r)] << endl;
	}
	return 0;
}

其他例题

【P3870】01 反转，区间求和

tag 表示一块是否反转；
sum 表示区间和，不考虑是否反转。

constexpr int N = 1e5 + 10;

int n, m, siz, cnt;
int belong[N], L[N], R[N];
int a[N], sum[N], tag[N];

void build() {
	siz = sqrt(n), cnt = (n - 1) / siz + 1;
	for (int i = 1; i <= n; ++i)
		belong[i] = (i - 1) / siz + 1;
	for (int i = 1; i <= cnt; ++i)
		L[i] = (i - 1) * siz + 1, R[i] = L[i] + siz - 1;
	R[cnt] = n;
}

void change(int l, int r) {
	int p = belong[l], q = belong[r];
	if (p == q) {
		for (int i = l; i <= r; ++i) {
			if (a[i] == 0) a[i] = 1, ++sum[p];
			else a[i] = 0, --sum[p];
		}
		return;
	}
	for (int i = l; i <= R[p]; ++i) {
		if (a[i] == 0) a[i] = 1, ++sum[p];
		else a[i] = 0, --sum[p];
	}
	for (int i = p + 1; i <= q - 1; ++i)
		tag[i] ^= 1; 
	for (int i = L[q]; i <= r; ++i) {
		if (a[i] == 0) a[i] = 1, ++sum[q];
		else a[i] = 0, --sum[q];
	}
}

int query(int l, int r) {
	int p = belong[l], q = belong[r];
	int res = 0;
	if (p == q) {
		for (int i = l; i <= r; ++i)
			res += a[i] ^ tag[p];
		return res;
	}
	for (int i = l; i <= R[p]; ++i)
		res += a[i] ^ tag[p];
	for (int i = p + 1; i <= q - 1; ++i) {
		if (!tag[i]) res += sum[i];
		else res += siz - sum[i];
	}
	for (int i = L[q]; i <= r; ++i)
		res += a[i] ^ tag[q];
	return res;
}

signed main() {
	cin >> n >> m;
	build();
	while (m--) {
		int op, l, r;
		cin >> op >> l >> r;
		if (op == 0) change(l, r);
		else cout << query(l, r) << endl;
	}
	return 0;
}

Reference

[1] https://blog.csdn.net/ZhuRanCheng/article/details/128854390
[2] https://yuhi.xyz/post/分块学习笔记/
[3] https://www.jianshu.com/p/2aba8f326052
[4] https://www.cnblogs.com/xyzqwq/p/fenkuai.html
[5] https://oi-wiki.org/ds/decompose/

posted @ 2024-08-04 16:52 RainPPR 阅读(10) 评论(0) 编辑收藏举报

刷新页面返回顶部

RainPPR（ツ）

逄沛然

数据结构——数列分块学习笔记

数据结构——数列分块学习笔记

基础思想

问题引入

基本结构

复杂度证明

分块的应用

简化实现

预处理

1 区间加、单点查询

4 区间加、区间查询

6 单点插入、单点查询

数列分块入门九题

2 区间加，区间排名

3 区间加，区间前驱

5 区间开方，区间查询

7 区间加乘，单点查询

8 区间计数，区间覆盖

9 区间最小众数

其他例题

【P3870】01 反转，区间求和

Reference

公告

RainPPR（ツ）

逄沛然

数据结构——数列分块 学习笔记

数据结构——数列分块 学习笔记

基础思想

问题引入

基本结构

复杂度证明

分块的应用

简化实现

预处理

1 区间加、单点查询

4 区间加、区间查询

6 单点插入、单点查询

数列分块入门九题

2 区间加，区间排名

3 区间加，区间前驱

5 区间开方，区间查询

7 区间加乘，单点查询

8 区间计数，区间覆盖

9 区间最小众数

其他例题

【P3870】01 反转，区间求和

Reference

公告

数据结构——数列分块学习笔记

数据结构——数列分块学习笔记