基础算法——表达式求值 学习笔记

基础算法——表达式求值 学习笔记

优先级和结合性

优先级：

• 优先级高的优先计算，优先级低的不优先计算，括号优先级最高；

• 本文只考虑【乘方，乘除，加减】三级二元运算，这三级优先级递减。

结合性：

• 左结合性：例如 \(a+b+c:=(a+b)+c\).

• 右结合性：例如 \(\mathrm{a^\wedge b^\wedge c}:=a^{\left(b^c\right)}\neq \left(a^b\right)^c\).

注意乘方是最常见的右结合性的运算符，处理这个运算特判即可。

基本表达式类型

• 前缀表达式（波兰表达式）：简记为，数字在前，符号在后。

• 后缀表达式（逆波兰表达式）：简记为，数字在后，符号在前。

• 中缀表达式：人类的表达式，符号在数字中间。

下文将直接通过表达式树讲解。

表达式树

我们对于一个表达式 \(S\)，

• 在这个表达式中，最后运算的符号作为根，

• 运算符两边的各自为一棵子树，表达式树的子树也是一棵表达式树。

形如，

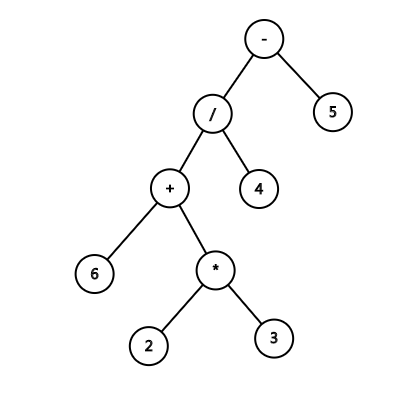
我们可以观察到一些性质，

• 非叶子节点一定是符号，叶子节点一定是数字；

• 每次合并两个数字，替换其父亲，最终根处就是表达式的值。

我们有（前中后指的是父亲的位置），

• 表达式树的前序遍历（父亲，左儿子，右儿子），就是前缀表达式。

• 表达式树的中序遍历（左儿子，父亲，右儿子），就是中缀表达式。

• 表达式树的后序遍历（左儿子，右儿子，父亲），就是后缀表达式。

• 同时，因为只有叶子节点是数值，因此前中后缀表达式不会改变数字的相对位置。

我们现在假设我们已经有表达式树了，考虑计算，

\[\begin{array}{ll} 1 & \text{calc}({root}) \\ 2 & \qquad \textbf{if } root \text{ is a leaf node} \\ 3 & \qquad \qquad \textbf{return } \text{the value of } root \\ 4 & \qquad \operatorname{op} \gets \text{the operator of } root \\ 5 & \qquad lval \gets \text{calc}(\text{the left son of } root) \\ 6 & \qquad rval \gets \text{calc}(\text{the right son of } root) \\ 7 & \qquad \textbf{return } lval \operatorname{op} rval \end{array} \]

但是我们通常得到的是一个中缀表达式，

如果按照表达式树的标准形式直接暴力运算，

\[\begin{array}{ll} 1 & \text{calc}({str}) \\ 2 & \qquad \textbf{if } str \text{ contains only one number} \\ 3 & \qquad \qquad \textbf{return } \operatorname{stod}(str) \\ 4 & \qquad op \gets \text{the last operator evaluated} \\ 5 & \qquad pos \gets \text{the position of operator } op \\ 5 & \qquad lval \gets \text{calc}(str[\dots,pos-1]) \\ 6 & \qquad rval \gets \text{calc}(str[pos+1,\dots]) \\ 7 & \qquad \textbf{return } lval \operatorname{op} rval \end{array} \]

我们一般需要 \(\mathcal O(n)\) 的找到最后运算的运算符的，

因此，这样暴力做，时间复杂度是可以被卡到 \(\mathcal O(n^2)\) 的。

例如：\(1+1+1+1+1+1+1+1+1+1+1\)。

我们先不考虑优化，先来几个简单的。

后缀表达式直接求值

例如，表达式，

\[\texttt{1 2 + 8 2 - 7 4 - / *} \]

我们记一个栈，数字栈 \(S\)，

• 从前往后考虑每一个字符，

• 如果是数字：直接加入数字栈 \(S\)。

• 如果是符号：取出栈顶两元素，进行运算后压入栈。

注意符号的操作顺序，

• 根据表达式树，我们的运算 \(a\otimes b\) 的 \(a\) 是先入栈、后出栈的，

• 因此顺序是先弹出的做 \(b\)，后弹出的做 \(a\)。

• 一般 \(+,\times\) 没有顺序要求，但是 \(-,\div\) 是有的。

代码（P1449 后缀表达式）：

inline int awa(int a, int b, char c) {
    if (c == '+') return a + b;
    if (c == '-') return a - b;
    if (c == '*') return a * b;
    if (c == '/') return a / b;
    __builtin_unreachable();
}

signed main() {
    stack<int> stk;
    char str[60] = {0};
    while (1) {
        int status = scanf("%[1234567890].", str);
        if (status == 0) {
            char c = getchar();
            if (c == '@') break;
            int a = stk.top(); stk.pop();
            int b = stk.top(); stk.pop();
            stk.push(awa(b, a, c));
        }
        else stk.push(stod(str));
    }
    cout << stk.top() << endl;
    return 0;
}

前缀表达式直接求值

和后缀表达式类似，

• 从后往前考虑每一个字符，

• 如果是数字：直接加入数字栈 \(S\)。

• 如果是符号：取出栈顶两元素，进行运算后压入栈。

注意符号的操作顺序，

• 根据表达式树，我们的运算 \(a\otimes b\) 的 \(a\) 是后入栈、先出栈的，

• 因此顺序是先弹出的做 \(a\)，后弹出的做 \(b\)。

• 一般 \(+,\times\) 没有顺序要求，但是 \(-,\div\) 是有的。

中缀表达式的后缀求值

我们不考虑仔细的证明，考虑观察结论，

• 对于 1 * 2 + 3 后缀表达式为 1 2 * 3 +；

• 对于 1 + 2 * 3 后缀表达式为 1 2 3 * +。

考虑从左到右遍历原表达式，

• 在第一个例子中，+ 使得 * 运算弹出；

• 在第二个例子中，* 并没有使 + 弹出。

我们大胆猜测结论，

• 加入一个运算符时，

• 其前面比他优先级高的运算符弹出，并同步计算；

• 将这个运算符压入栈。

于是，我们要维护一个优先级非严格单调递增的操作符序列。

每次加入时，按照上面的操作弹栈，使得序列依旧有序，那么这就是个单调栈。

注意到乘方的右结合性，同时优先级最高，

我们只需要特判，没有任何运算符（括号除外）可以弹出乘方即可。

代码（AcWing 3302 表达式求值）：

int pri[256];

stack<int> num;

stack<char> op;

void init() {
    pri['+'] = pri['-'] = 1;
    pri['*'] = pri['/'] = 2;
    pri['^'] = 3;
}

int powi(int a, int b) {
    int r = 1;
    for (; b; b >>= 1) {
        if (b & 1) r = r * a;
        a = a * a;
    }
    return r;
}

inline int awa(int a, int b, char c) {
    if (c == '+') return a + b;
    if (c == '-') return a - b;
    if (c == '*') return a * b;
    if (c == '/') return a / b;
    if (c == '^') return powi(a, b);
    __builtin_unreachable();
}

void eval() {
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    char c = op.top(); op.pop();
    num.push(awa(a, b, c));
}

int calc(string str) {
    int n = str.size();
    for (int i = 0; i < n; ++i) {
        if (isdigit(str[i])) {
            int r = 0, j = i;
            while (j < n && isdigit(str[j])) {
                r = r * 10 + str[j] - '0';
                ++j;
            }
            i = j - 1, num.push(r);
        }
        else if (str[i] == '(') op.push('(');
        else if (str[i] == ')') {
            while (op.top() != '(') eval();
            op.pop();
        }
        else if (str[i] == '^') op.push('^');
        else {
            while (!op.empty() && pri[op.top()] >= pri[str[i]])
                eval();
            op.push(str[i]);
        }
    }
    while (!op.empty()) eval();
    return num.top();
}

中缀表达式转后缀表达式

首先我们注意到上面的代码本质就是后缀表达式的形式。

我们把前面 eval 函数魔改一下就可以了（改成加入到后缀表达式中）。

另外前面的结论，后缀表达式数字顺序不变，我们在弹出的时候加入符号即可。

代码：

int pri[256];

struct node {
    int type;
    union {
        int num;
        char op;
    } val;
    node() = default;
    node(int num): type(0) { val.num = num; }
    node(char op): type(1) { val.op = op; }
    friend ostream& operator <<(ostream &out, const node a) {
        if (a.type) out << a.val.op;
        else out << a.val.num;
        return out;
    }
};

stack<char> op;

vector<node> res;

void init() {
    pri['+'] = pri['-'] = 1;
    pri['*'] = pri['/'] = 2;
    pri['^'] = 3;
}

void eval() {
    res.emplace_back((char)op.top());
    op.pop();
}

void calc(string str) {
    int n = str.size();
    for (int i = 0; i < n; ++i) {
        if (isdigit(str[i])) {
            int r = 0, j = i;
            while (j < n && isdigit(str[j])) {
                r = r * 10 + str[j] - '0';
                ++j;
            }
            i = j - 1, res.emplace_back(r);
        }
        else if (str[i] == '(') op.emplace('(');
        else if (str[i] == ')') {
            while (op.top() != '(') eval();
            op.pop();
        }
        else if (str[i] == '^') op.emplace('^');
        else {
            while (!op.empty() && pri[op.top()] >= pri[str[i]])
                eval();
            op.emplace(str[i]);
        }
    }
    while (!op.empty()) eval();
}

附：我在 P1175 表达式的转换 的抽象输出代码。

int pre[10100], del[10100];

void print() {
    for (int i = 0; i < (int)res.size(); ++i) {
        if (del[i]) continue;
        cout << res[i] << " ";
    }
    cout << endl;
}

void welcome() {
    for (int i = 0; i < (int)res.size(); ++i) {
        pre[i + 1] = i;
        if (!res[i].type) continue;
        print();
        res[pre[pre[i]]].val.num = awa(
            res[pre[pre[i]]].val.num,
            res[pre[i]].val.num,
            res[i].val.op
        );
        del[pre[i]] = del[i] = 1;
        pre[i + 1] = pre[pre[i]];
    }
    print();
}

前缀表达式与运算函数

首先还是前面的结论：前缀表达式不改变数字相对顺序。

我们可以发现一个有意思的结论，表达式转为前缀后，例如，

\[\begin{aligned} &(6+2\times3)\div4-5\\ \to\;&\texttt{- / + 6 * 2 3 4 5}\\ \to\;&\texttt{-(/(+(6, *(2, 3)), 4), 5)}\\ \to\;&\texttt{minus(divide(plus(6, multiply(2, 3)), 4), 5)} \end{aligned} \]

我们就可以将一个只由函数和数字组合的表达式，

• 通过拆括号和去逗号的方式转为前缀表达式，

• 在循环运算的时候甚至可以直接跳过这些省略的字符。

因此，我们就找到了一种全新的表达式计算方法，

• 递归处理前缀表达式，是数字的时候直接跳过。

全文完。

---

参考 @tiger2005 的，

• 浅谈表达式的求值（Vol.1 后缀表达式）

• 浅谈表达式的求值（Vol.2 进阶）