电学——基尔霍夫电路定律 学习笔记

电学——基尔霍夫电路定律 学习笔记

基尔霍夫电路定律（基尔霍夫定律）涉及了电荷的守恒及电势的保守性，指的是两条电路学定律：

基尔霍夫电流定律（基尔霍夫第一定律，KCL）、基尔霍夫电压定律（基尔霍夫第二定律，KVL）。

基本概念

1. 支路：

   • 每个元件就是一条支路。
   • 串联的元件我们视它为一条支路。
   • 在一条支路中电流处处相等。

2. 节点：

   • 支路与支路的连接点。
   • 两条以上的支路的连接点。

3. 回路：

   • 闭合的支路。
   • 闭合节点的集合。

适用范围

基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上，在稳恒电流条件下严格成立。

当基尔霍夫第一、第二方程组联合使用时，可正确迅速地计算出电路中各支路的电流值。

对于含有电感器的电路，必需将基尔霍夫电压定律加以修正。

由于含时电流的作用，电路的每一个电感器都会产生对应的电动势 \(E_k\)。

必需将这电动势纳入基尔霍夫电压定律，才能求得正确答案。

基尔霍夫电流定律（基尔霍夫第一定律，KCL）

定义：所有进入某节点的电流的总和等于所有离开这节点的电流的总和。

或者：设电流流入为正，流出为负，则所有涉及某节点的电流的代数和等于零。

基尔霍夫电流定律是节点分析的基础定律。

对于方程表达：\(\sum i_k=0\)；其中，\(i_k\) 是与这节点相连接的第 \(k\) 个支路的电流。

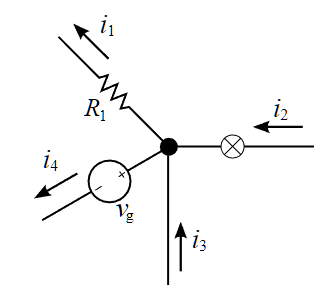
如图，有 \(i_2+i_3=i_1+i_4\)，或者可以写成 \(i_2+i_3-i_1-i_4=0\) 的形式。

基尔霍夫电压定律（基尔霍夫第二定律，KVL）

定义：沿着闭合回路所有器件两端的电势差（电压）的代数和等于零。

或者：沿着闭合回路的所有电动势的代数和等于所有电压降的代数和。

基尔霍夫电压定律是网目分析的基础定律。

对于方程表示：\(\sum v_k=0\)；其中，\(v_k\) 是器件两端的电压。

基尔霍夫电压定律不仅应用于闭合回路，也可以把它推广应用于回路的部分电路。

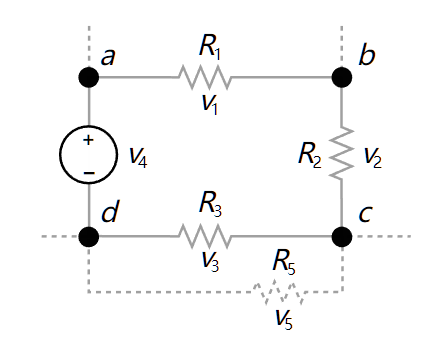
如图，有 \(v_1+v_2+v_3=v_4\)，或者可以写成 \(v_1+v_2+v_3-v_4=0\) 的形式。

例题

第一题

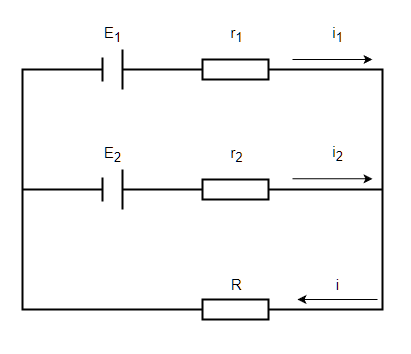
可以列出三个式子：

\[\left\{\begin{array}{c} E_1&=&i_1r_1+iR\\ E_2&=&i_2r_2+iR\\ i&=&i_1+i_2 \end{array}\right. \]

已知 \(E_1,E_2,r_1,r_2,R\)，可以求出 \(i_1,i_2,i\)。

第二题

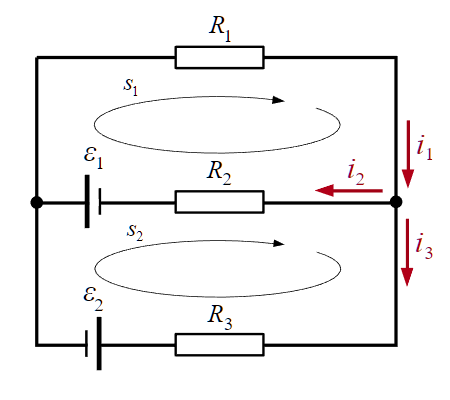
根据基尔霍夫第一定律：

\[i_1=i_2+i_3 \]

将基尔霍夫第二定律应用于回路 \(s_1\)：

\[\mathcal{E}_1=R_1i_1+R_2i_2 \]

将基尔霍夫第二定律应用于回路 \(s_2\)：

\[\mathcal{E}_1+\mathcal{E}_2+R_3i_3=R_2i_2 \]

已知：\(R_1=100\Omega\)，\(R_2=200\Omega\)，\(R_3=300\Omega\)，\(\mathcal{E}_1=3V\)，\(\mathcal{E}_2=4V\)。

解得：

\[\left\{\begin{array}{c} i_1&=&1/1100&A\\ i_2&=&4/275&A\\ i_3&=&-3/220&A \end{array}\right. \]

注意到电流 \(i_3\) 带了负号，这意味着我们 \(i_3\) 的假定方向不正确。

这也意味着基尔霍夫电路定律解题不完全需要电流方向已知。