[点分治] 点分治入门
练习题:
欢迎来到我的博客https://www.cnblogs.com/Railgun000
各位同学们大家好,
今天我们来研究一下点分治.
那么什么是点分治?
顾名思义就是基于结点来分治,
是树分治的一种,
能够处理大规模的树上路径信息问题.
点分治比较模板化,通常分为4大部分
1.求树的重心函数 getroot()
2.计算所有结点到根节点的距离函数 caldis()
3.计算合法路径函数 sovle()
4.点分治函数 dfz()
下面通过一道例题来感受一下
链接:https://www.luogu.com.cn/problem/P3806
给定一颗n个结点的无根树,
有m次询问,
每次询问树上距离为k的点对是否存在.
第一行两个数 n,m。
接下来 n-1 条边 a,b,c 描述 a 到 b 有一条长度为 c 的路径。
接下来 m 行每行询问一个 K。
对于每个 K 每行输出一个答案,
存在输出 AYE,
否则输出 NAY。
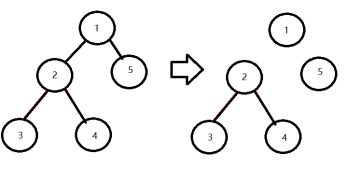
我们知道有根树是要有根的,
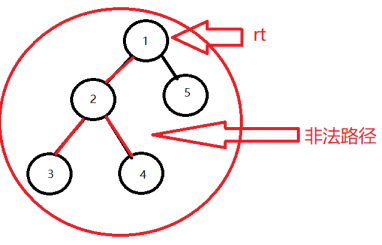
所以我们先随便找一个点作为根rt.
那么接下来的问题就是这颗树上有没有距离为k的点对.
那么接下来看看会出现什么样的点对.
对于当前根rt,
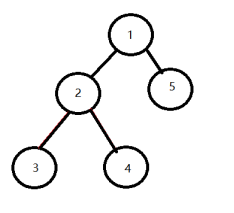
所有位于其子树中的路径可分为2种,
一种是路径经过rt,
一种是路径不经过rt如图所示,
红色的就是路径.
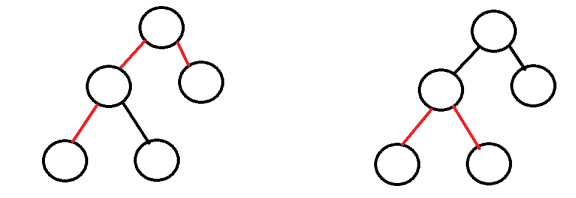
对于经过rt的路径又可分为两种,
左图为以rt为端点的路径
右图为不以rt为端点的路径
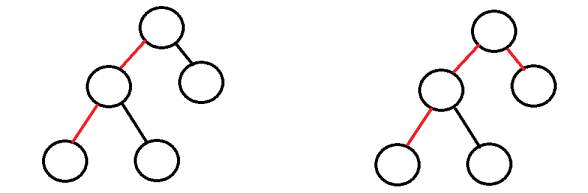
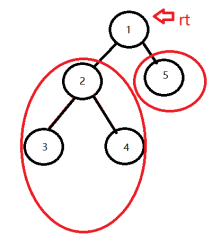
对于两端都不是根rt的情况,
可由以rt为端点的路径合成
如下图所示.
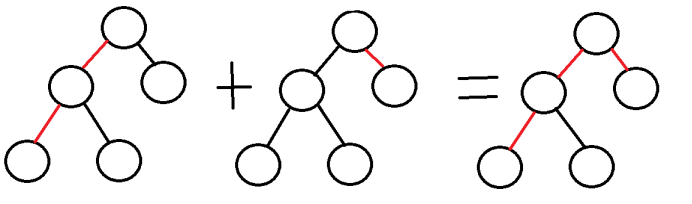
由此我们发现,以rt为端点的路径是最基本的一种情况,
我们设dis[u]表示点u到rt的距离,
因为不以rt为端点的路径,
可以由以rt为端点的路径合成,
即u到v的距离为dis[u]+dis[v],
而若路径不经过rt,
则它必定会经过当前树T中的某个点x,
那么可将这个点x作为根结点形成一颗子树,
转化为路径经过根节点的情况,
并重新计算dis数组来求解.
到这里,我们想给这两种路径起一个名字,
为了方便表示与理解,
对于以rt为端点的路径,称之为"基本路径"
(为什么给它起这个名字?
因为这种路径对于这个问题来说是最基本的情况).
对于不以rt为端点的路径,称之为"组合路径"
(为什么给它起这个名字?
因为这种路径是有两条在不同子树中的基本路径组成的,
注意这个组合路径的概念,我接下来会有解释)
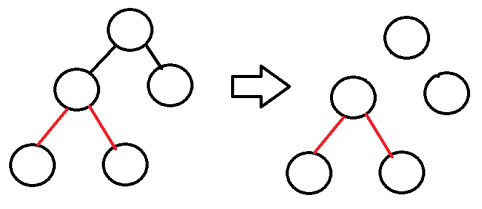
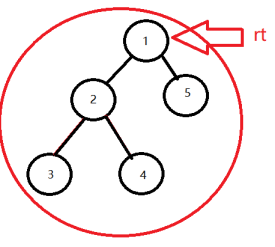
这里要注意一个问题,
如果一个路径是组合路径,
那么组成这条路径的两个基本路径
必在以rt孩子结点ch组成的不同子树中.
也就是说,不是任一两个基本路径都能组合成组合路径
为什么呢?
可以用反证法证明,
如果在同以子树中选择两个不同的基本路径,
那么这两条基本路径必定会有共同的rt与ch的边,
那么这两个基本路径组成的就不是一条简单路径(就是没有重复边的路径),
而这种情况是不能存在的.
如图所示.

所以在同一子树中
我们检查基本路径是否合法,
在不同子树中,
我们只能将不同子树间的基本路径两两组合成为组合路径来检查路径是否合法.
那么这个dis数组该如何计算?
我们知道dis[u]代表u到rt的距离,
同时我们还已知两个相邻点的边权.
所以如果这个结点u是rt的孩子,
那么dis[u]==边权.
如果要求u的孩子v到rt的距离dis[v]呢?
那么就是dis[v]=dis[u]+u到v的边权,
这是一个自顶向下的过程,
如此递推下去,
就可以计算出dis数组,
为了方便处理,
我们可以把每次算出的dis记录下来
既然要递归,
那我们就写个函数,
这就是点分治中的计算所有结点到根节点的距离函数,
当然这个只是基本部分,我们后续还要对这部分进行修改.
caldis函数
1 int dis[amn],di[amn],tp; 2 void caldis(int u,int fa){ 3 if(dis[u]>(int)1e7)return; 4 di[++tp]=dis[u]; 5 for(int i=head[u];i;i=eg[i].nxt){ 6 int v=eg[i].v,w=eg[i].w; 7 if(vis[v]||v==fa)continue; 8 dis[v]=dis[u]+w; 9 caldis(v,u); 10 } 11 }
现在我们知道了路径的几种组成,
知道了dis数组该怎么算,
接着就要来解决这颗树中是否存在距离为k的点对.
首先要将rt打上访问标记,不再访问rt结点
对于经过根rt的路径,我们可以枚举其子结点ch为根的ch子树(ch结点及其后裔结点)
计算ch子树中所有结点到rt的距离dis,
每次处理完dis数组后,
都看看现在和曾经处理出的dis中有没有距离为k的点对,
或者是有没有现在处理出的某个dis与之前处理出的某个dis之和距离为k. 如果有就将答案记录下来.
这里的dis与之前处理过的dis组合就是之前说的在不同子树中的基本路径才可以两两组合来检查路径是否合法,
可以说曾经处理过的基本路径必定与当前的基本路径在以rt的孩子ch结点形成的不同的子树中.
有了一个大概的思路后就是怎么实现的问题了.
现在我们面临的问题是如何知道
现在和曾经算出来的dis及其组合
是否存在恰好等于k的点对.
首先我们看看如何知道dis数组中是否存在距离为k的路径?
很简单,每次算完dis后看他是否为k就好了.
那么如何查询有没有现在处理出的某个dis与之前处理出的某个dis之和距离为k?
注意到dis[u]+dis[v]==k,
如果我们现在已知k和dis[v],
那么dis[v]就可以通过k-dis[u]求解出来.
注意到若k==dis[u],则k-dis[u]==0,
同时我们观察到题目上k的数据范围最大到1e7,
如果开全局数组是存的下的.
这里有个非常重要的点是注意不要数组越界,
因为有可能算出来的dis是大于1e7的,
但你又只开了1e7大小的数组,这样你就会RE.
所以之前caldis函数中才会限定dis不能超过1e7
如果超过了函数就返回
所以我们用数组来标记曾经处理过的距离,
我把这个数组命名为jg,
这个数组的下标就表示距离,类似桶排序的表示方法
如果k-dis[u]存在,则说明以前处理过一个dis[v],
而且这个结点v是与结点u在不同子树中的,并且dis[u]+dis[v]==k
注意这里要将询问离线,
集中处理m次询问,
调用1次点分治,
如果调用m次点分治是会超时的.
Jg数组是判断以前有没有处理过一个距离能与当前这个距离组合等于k,
所以我们是先判断路径,再把当前算出的距离到jg数组里标记.
把当前这个根节点rt处理完后还要清空jg数组,
在清空jg数组时不要直接用memset,
否则你有可能会TLE
,应该用个队列或栈之类的把使用过的距离存起来,
用过数组的哪个位置就清空那个位置.
sovle函数
1 bool jg[(int)1e7+5]; 2 int ans[amn]; 3 queue<int> bk; 4 void sovle(int u){ 5 jg[0]=1; 6 bk.push(0); 7 for(int i=head[u];i;i=eg[i].nxt){ 8 int v=eg[i].v,w=eg[i].w; 9 if(vis[v])continue; 10 tp=0; 11 dis[v]=w; 12 caldis(v,u); 13 for(int j=1;j<=tp;j++){ 14 for(int k=1;k<=m;k++){ 15 if(K[k]>=di[j])ans[k]+=jg[K[k]-di[j]]; 16 } 17 } 18 for(int j=1;j<=tp;j++){ 19 jg[di[j]]=1; 20 bk.push(di[j]); 21 } 22 } 23 while(bk.size()){ 24 jg[bk.front()]=0; 25 bk.pop(); 26 } 27 }
下面是一个点分治的计算路径的过程,
首先要将rt打上访问标记,不再访问rt结点
然后caldis算出所有基本路径
接着是算组合路径
同时处理这些路径
然后再递归其他结点作为新的根
直到没有结点可以递归为止
|
Root |
基本路径 |
组合路径 |
|
1 |
(1,2) |
(2,5) |
|
|
(1,3) |
(3,5) |
|
|
(1,4) |
(4,5) |
|
|
(1,5) |
|
|
|
|
|
|
2 |
(2,3) |
(3,4) |
|
|
(2,4) |
|
|
|
|
|
|
5 |
无 |
无 |
|
|
|
|
|
3 |
无 |
无 |
|
|
|
|
|
4 |
无 |
无 |
在上表中,
可以看出暴力算出所有路径的方法是O(n*n),
只算基本路径并组合基本路径的方法
可以将求路径这部分的复杂度降到O(n)
我们已经知道了如何计算路径距离,
如何判断合法路径,那么这就足够了吗?
假设输入的数据是一条链,
而我们一开始是随机找的根结点,
那么最坏情况下选了这条链的端点的话这颗树的深度就为n,
需要递归处理n层,
所以我们的根不能随便选.
为了让处理的子树深度尽可能小,
所以我们每次点分治前选择树的重心作为根节点.
这样数的深度是logn的,
递归处理也就只需要logn层.
那么怎么如何找到重心呢?
我们先来看看重心的定义:
树的重心就是最大子树结点数最小的点.
所以我们要统计子树结点数,
接着要统计出一个结点的最大子树结点数
(这里的最大子树结点数
不仅包括当前根向下的子树,
还包括向上的子树,
上面子树的求法
就是总点数减去向下子树的点数),
然后要维护一个最大子树结点数最小的点.
这些信息可以在dfs回溯时记录.
类似求树的直径,
求两次dfs,先找一个点dfs得到一个根,再用这个根dfs找出树的重心.
求重心函数
1 int siz[amn],maxt[amn],vis[amn],rt; 2 void calsiz(int u,int fa,int sum){ 3 siz[u]=1; 4 maxt[u]=0; 5 for(int i=head[u];i;i=eg[i].nxt){ 6 int v=eg[i].v; 7 if(vis[v]||v==fa)continue; 8 calsiz(v,u,sum); 9 siz[u]+=siz[v]; 10 maxt[u]=max(maxt[u],siz[v]); 11 } 12 maxt[u]=max(maxt[u],sum-siz[u]); 13 if(maxt[u]<maxt[rt])rt=u; 14 } 15 void getroot(int u,int fa,int sum){ 16 rt=0; 17 maxt[rt]=inf; 18 calsiz(u,fa,sum); 19 20 }
这里还需要注意一个问题,
在点分治中,
每处理完一个结点后
就要删去这个结点以防止重复计算,
那么总结点数sum是会改变的,
每次重新选择根结点后要更新sum
那么这个sum是多少呢?
就是siz[u],
即上次找重心时这个点u的子树大小.
为什么呢?
因为你这次处理完后rt结点删掉了,
那么点u和rt的路径就断掉了,
以u为根节点的子树就成为了一个连通块,
那么这个连通块的大小就是以u为根节点的子树的大小siz[u].
点分治函数
1 void dfz(int u){ 2 vis[u]=1; 3 sovle(u); 4 for(int i=head[u];i;i=eg[i].nxt){ 5 int v=eg[i].v; 6 if(vis[v])continue; 7 getroot(v,u,siz[v]); 8 dfz(rt); 9 } 10 }
接下来我们来看下代码
链式前向星

1 int head[amn],etot; 2 struct edge{ 3 int nxt,v; 4 edge(){} 5 edge(int nxt,int v):nxt(nxt),v(v){} 6 }eg[amn]; 7 void init(){ 8 etot=0; 9 memset(head,0,sizeof head); 10 } 11 void add(int u,int v){ 12 eg[++etot]=edge(head[u],v); 13 head[u]=etot; 14 }
如果是多组输入,链式前向星要初始化etot和head数组
完整代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int amn=1e5+5,inf=1e9; 4 int n,m,K[amn]; 5 6 int head[amn],etot; 7 struct edge{ 8 int nxt,v,w; 9 }eg[amn]; 10 void add(int u,int v,int w){ 11 eg[++etot]={head[u],v,w}; 12 head[u]=etot; 13 } 14 15 int siz[amn],maxt[amn],vis[amn],rt; 16 void calsiz(int u,int fa,int sum){ 17 siz[u]=1; 18 maxt[u]=0; 19 for(int i=head[u];i;i=eg[i].nxt){ 20 int v=eg[i].v; 21 if(vis[v]||v==fa)continue; 22 calsiz(v,u,sum); 23 siz[u]+=siz[v]; 24 maxt[u]=max(maxt[u],siz[v]); 25 } 26 maxt[u]=max(maxt[u],sum-siz[u]); 27 if(maxt[u]<maxt[rt])rt=u; 28 } 29 void getroot(int u,int fa,int sum){ 30 rt=0; 31 maxt[rt]=inf; 32 calsiz(u,fa,sum); 33 calsiz(rt,-1,sum); 34 } 35 36 int dis[amn],di[amn],tp; 37 void caldis(int u,int fa){ 38 if(dis[u]>(int)1e7)return; 39 di[++tp]=dis[u]; 40 for(int i=head[u];i;i=eg[i].nxt){ 41 int v=eg[i].v,w=eg[i].w; 42 if(vis[v]||v==fa)continue; 43 dis[v]=dis[u]+w; 44 caldis(v,u); 45 } 46 } 47 48 bool jg[(int)1e7+5]; 49 int ans[amn]; 50 queue<int> bk; 51 void sovle(int u){ 52 jg[0]=1; 53 bk.push(0); 54 for(int i=head[u];i;i=eg[i].nxt){ 55 int v=eg[i].v,w=eg[i].w; 56 if(vis[v])continue; 57 tp=0; 58 dis[v]=w; 59 caldis(v,u); 60 for(int j=1;j<=tp;j++){ 61 for(int k=1;k<=m;k++){ 62 if(K[k]>=di[j])ans[k]+=jg[K[k]-di[j]]; 63 } 64 } 65 for(int j=1;j<=tp;j++){ 66 jg[di[j]]=1; 67 bk.push(di[j]); 68 } 69 } 70 while(bk.size()){ 71 jg[bk.front()]=0; 72 bk.pop(); 73 } 74 } 75 void dfz(int u){ 76 vis[u]=1; 77 sovle(u); 78 for(int i=head[u];i;i=eg[i].nxt){ 79 int v=eg[i].v; 80 if(vis[v])continue; 81 getroot(v,u,siz[v]); 82 dfz(rt); 83 } 84 } 85 int main(){ 86 int a,b,c; 87 scanf("%d%d",&n,&m); 88 for(int i=1;i<=n-1;i++){ 89 scanf("%d%d%d",&a,&b,&c); 90 add(a,b,c); 91 add(b,a,c); 92 } 93 for(int i=1;i<=m;i++){ 94 scanf("%d",&K[i]); 95 } 96 getroot(1,-1,n); 97 dfz(rt); 98 for(int i=1;i<=m;i++){ 99 if(ans[i])printf("AYE\n"); 100 else printf("NAY\n"); 101 } 102 } 103 /** 104 8 1 105 1 2 1 106 2 3 1 107 2 4 1 108 1 5 9 109 5 6 9 110 1 7 9 111 1 8 9 112 4 113 */
接下来我们再来看一道题
链接:https://www.luogu.com.cn/problem/P4178
给你一棵TREE,以及这棵树上边的距离.问有多少对点它们两者间的距离小于等于K
输入一个N(n<=40000) 接下来n-1行边描述管道,按照题目中写的输入 接下来是k
输出占一行,内容为有多少对点之间的距离小于等于k
k≤2e4,wi≤1e3
这道题和刚才那道题的区别主要在于
从判断是否存在距离为k的路径
转化为距离小于等于k的路径数量有多少.
我们就顺着题意思考,
判断一条基本路径的长度是否小于等于k很容易,
那么如何知道
当前这条基本路径与不同子树的基本路径组合小于等于k的有多少个?
这里有2种方案
方案1:树状数组
设当前基本路径为dis[u],
曾经处理过的基本路径为dis[v],
合法的组合路径为dis[u]+dis[v]<=k.
那么我们当前已经处理出了dis[u],且题目给出了k,
所以当前的问题就是存在多少合法的dis[v](1<=dis[v]<=k-dis[u]).
每处理一个距离,就询问小于等于某个值的距离的数量,
当前子树的路径处理完后更新数组中距离的数量
我们可以用树状数组实现,
代码量小很好写,
只是这里写树状数组时要注意一下单点修改时要设上限,
不然就会一直修改停不下来,
这个地方比较容易在手速快时被忽略.
树状数组
1 const int bitsiz=2e5+5; 2 int bit[bitsiz]; 3 int lowbit(int x){return x&-x;} 4 void add_bit(int x,int k){ 5 while(x<=bitsiz){ 6 bit[x]+=k; 7 x+=lowbit(x); 8 } 9 } 10 int getsum(int x){ 11 int ans=0; 12 while(x){ 13 ans+=bit[x]; 14 x-=lowbit(x); 15 } 16 return ans; 17 }
这道题可以直接拿刚才的代码来修改,
在caldis函数时如果dis[u]>k就返回.
dfz函数的jg数组改为树状数组,
处理di数组那部分改为如果di[j]==k时ans++,
并且ans再加上曾经处理过的距离小于等于k-di[j]的路径的个数
(这里用树状数组实现),
di数组处理完后,
将di数组的所有元素在树状数组中的di[j]位置加1,
并同时放进bk数组中等待清除.
在处理bk队列时
改为在将bk队首元素在树状数组中的bk队首元素位置减1,
接着再改下main函数和一些参数,基本上就可以AC了.
接下来我们来看下代码
sovle代码
1 int ans; 2 queue<int> bk; 3 void sovle(int u){ 4 for(int i=head[u];i;i=eg[i].nxt){ 5 int v=eg[i].v,w=eg[i].w; 6 if(vis[v])continue; 7 dis[v]=w; 8 tp=0; 9 caldis(v,u); 10 for(int j=1;j<=tp;j++){ 11 ans+=(di[j]<=k?1:0); 12 if(k>di[j])ans+=getsum(k-di[j]); 13 } 14 for(int j=1;j<=tp;j++){ 15 add_bit(di[j],1); 16 bk.push(di[j]); 17 } 18 } 19 while(bk.size()){ 20 add_bit(bk.front(),-1); 21 bk.pop(); 22 } 23 }
完整代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int amn=1e5+5,inf=1e9,top=2e4+5; 5 6 int n,a,b,c,k; 7 8 int head[amn],egnum; 9 struct edge{ 10 int nxt,v,w; 11 edge(){} 12 edge(int nxt,int v,int w):nxt(nxt),v(v),w(w){} 13 }eg[amn]; 14 void add(int u,int v,int w){ 15 eg[++egnum]=edge(head[u],v,w); 16 head[u]=egnum; 17 } 18 19 int siz[amn],maxt[amn],rt,vis[amn]; 20 void calsiz(int u,int fa,int sum){ 21 siz[u]=1; 22 maxt[u]=0; 23 for(int i=head[u];i;i=eg[i].nxt){ 24 int v=eg[i].v; 25 if(vis[v]||v==fa)continue; 26 calsiz(v,u,sum); 27 siz[u]+=siz[v]; 28 maxt[u]=max(maxt[u],siz[v]); 29 } 30 maxt[u]=max(maxt[u],sum-siz[u]); 31 if(maxt[u]<maxt[rt])rt=u; 32 } 33 void getroot(int u,int fa,int sum){ 34 rt=0; 35 maxt[rt]=inf; 36 calsiz(u,fa,sum); 37 calsiz(rt,-1,sum); 38 } 39 40 int dis[amn],di[amn],tp; 41 void caldis(int u,int fa){ 42 if(dis[u]>k)return ; 43 di[++tp]=dis[u]; 44 for(int i=head[u];i;i=eg[i].nxt){ 45 int v=eg[i].v,w=eg[i].w; 46 if(vis[v]||v==fa)continue; 47 dis[v]=dis[u]+w; 48 caldis(v,u); 49 } 50 } 51 52 const int bitsiz=2e5+5; 53 int bit[bitsiz]; 54 int lowbit(int x){return x&-x;} 55 void add_bit(int x,int k){ 56 while(x<=bitsiz){ 57 bit[x]+=k; 58 x+=lowbit(x); 59 } 60 } 61 int getsum(int x){ 62 int ans=0; 63 while(x){ 64 ans+=bit[x]; 65 x-=lowbit(x); 66 } 67 return ans; 68 } 69 70 int ans; 71 queue<int> bk; 72 void sovle(int u){ 73 for(int i=head[u];i;i=eg[i].nxt){ 74 int v=eg[i].v,w=eg[i].w; 75 if(vis[v])continue; 76 dis[v]=w; 77 tp=0; 78 caldis(v,u); 79 for(int j=1;j<=tp;j++){ 80 ans+=(di[j]<=k?1:0); 81 if(k>di[j])ans+=getsum(k-di[j]); 82 } 83 for(int j=1;j<=tp;j++){ 84 add_bit(di[j],1); 85 bk.push(di[j]); 86 } 87 } 88 while(bk.size()){ 89 add_bit(bk.front(),-1); 90 bk.pop(); 91 } 92 } 93 void dfz(int u){ 94 vis[u]=1; 95 sovle(u); 96 for(int i=head[u];i;i=eg[i].nxt){ 97 int v=eg[i].v; 98 if(vis[v])continue; 99 getroot(v,u,siz[v]); 100 dfz(rt); 101 } 102 } 103 104 int main(){ 105 scanf("%d",&n); 106 for(int i=1;i<n;i++){ 107 scanf("%d%d%d",&a,&b,&c); 108 add(a,b,c); 109 add(b,a,c); 110 } 111 scanf("%d",&k); 112 ans=0; 113 getroot(1,-1,n); 114 dfz(rt); 115 printf("%d\n",ans); 116 }
方案2:双指针
之前我们是每次计算rt的基本路径
然后再将不同子树的基本路径组合为组合路径
现在我们直接算出在以rt为根的树中所有结点(包括rt结点)
到rt的距离记录在数组di中,计算di[x]+di[y]<=k的个数.
设di现在的大小为tp,x=1,y=tp.
因为我们算了rt到rt的距离为0,所以现在di[x]=0,di[x]+di[y]=di[y].
在x==1的情况下,
如果di[x]+di[y]>k且x<y则y--,当x<y且di[x]+di[y]<=k时,
则说明有y-x个基本路径符合条件,ans+=y-x,接着x++.
此时若x<y,则说明di[x]!=0,开始计算组合路径了.
若di[x]+di[y]>k且x<y则y--,
若x<y且di[x]+di[y]<=k时,则,ans+=y-x,接着x++.
直到x==y结束循环.
注意,为了避免重复计算,
我们需要先对di数组进行排序后
再进行这个运算.

sovle函数
1 int sovle(int u,int fa,int w){ 2 dis[u]=w; 3 tp=0;///记得要初始化栈!!! 4 caldis(u,fa); 5 sort(di+1,di+1+tp); 6 int l=1,r=tp,ans=0; 7 while(l<r){ 8 if(di[l]+di[r]<=k){ 9 ans+=r-l; 10 l++; 11 } 12 else r--; 13 } 14 return ans; 15 }
这样会算出在同一子树中的路径符合di[x]+di[y]<=k的情况,
这种情况的非法的,
所以我们需要在答案中减掉这些路径.
我们要在答案中减掉
加上了rt到ch的那条边的边权的情况下,
符合di[x]+di[y]<=k的路径数量.
接下来我们来看下代码
点分治函数
1 int ans; 2 void dfz(int u){ 3 vis[u]=1; 4 ans+=sovle(u,-1,0); 5 for(int i=head[u];i;i=eg[i].nxt){ 6 int v=eg[i].v,w=eg[i].w; 7 if(vis[v])continue; 8 ans-=sovle(v,u,w); 9 getroot(v,u,siz[v]); 10 dfz(rt); 11 } 12 }
完整代码

1 #include<stdio.h> 2 #include<iostream> 3 #include<queue> 4 #include<string.h> 5 #include<algorithm> 6 using namespace std; 7 typedef long long ll; 8 const int amn=2e5+5,inf=2e9,top=2e4+5; 9 10 int n,a,b,c,k; 11 12 int head[amn],egnum; 13 struct edge{ 14 int nxt,v,w; 15 edge(){} 16 edge(int nxt,int v,int w):nxt(nxt),v(v),w(w){} 17 }eg[amn]; 18 void add(int u,int v,int w){ 19 eg[++egnum]=edge(head[u],v,w); 20 head[u]=egnum; 21 } 22 23 int siz[amn],maxt[amn],rt,vis[amn]; 24 void calsiz(int u,int fa,int sum){ 25 siz[u]=1; 26 maxt[u]=0; 27 for(int i=head[u];i;i=eg[i].nxt){ 28 int v=eg[i].v; 29 if(vis[v]||v==fa)continue; 30 calsiz(v,u,sum); 31 siz[u]+=siz[v]; 32 maxt[u]=max(maxt[u],siz[v]); 33 } 34 maxt[u]=max(maxt[u],sum-siz[u]); 35 if(maxt[u]<maxt[rt])rt=u; 36 } 37 void getroot(int u,int fa,int sum){ 38 rt=0; 39 maxt[rt]=inf; 40 calsiz(u,fa,sum); 41 calsiz(rt,-1,sum); 42 } 43 44 int dis[amn],di[amn],tp; 45 void caldis(int u,int fa){ 46 if(dis[u]>k)return ; ///防溢出 47 di[++tp]=dis[u]; 48 for(int i=head[u];i;i=eg[i].nxt){ 49 int v=eg[i].v,w=eg[i].w; 50 if(vis[v]||v==fa)continue; 51 dis[v]=dis[u]+w; 52 caldis(v,u); 53 } 54 } 55 56 int sovle(int u,int fa,int w){ 57 dis[u]=w; 58 tp=0;///记得要初始化栈!!! 59 caldis(u,fa); 60 sort(di+1,di+1+tp); 61 int l=1,r=tp,ans=0; 62 while(l<r){ 63 if(di[l]+di[r]<=k){ 64 ans+=r-l; 65 l++; 66 } 67 else r--; 68 } 69 return ans; 70 } 71 72 int ans; 73 void dfz(int u){ 74 vis[u]=1; 75 ans+=sovle(u,-1,0); 76 for(int i=head[u];i;i=eg[i].nxt){ 77 int v=eg[i].v,w=eg[i].w; 78 if(vis[v])continue; 79 ans-=sovle(v,u,w); 80 getroot(v,u,siz[v]); 81 dfz(rt); 82 } 83 } 84 int main(){ 85 scanf("%d",&n); 86 for(int i=1;i<n;i++){ 87 scanf("%d%d%d",&a,&b,&c); 88 add(a,b,c); 89 add(b,a,c); 90 } 91 scanf("%d",&k); 92 ans=0; 93 getroot(1,-1,n); 94 dfz(rt); 95 printf("%d\n",ans); 96 }
感谢观看,由于水平所限,本文如有错误,请务必指出,谢谢各位巨佬!






