[尊老爱幼] Queen

You are given a rooted tree with vertices numerated from 1 to n

. A tree is a connected graph without cycles. A rooted tree has a special vertex named root.

Ancestors of the vertex i

are all vertices on the path from the root to the vertex i, except the vertex i itself. The parent of the vertex i is the nearest to the vertex i ancestor of i. Each vertex is a child of its parent. In the given tree the parent of the vertex i is the vertex pi. For the root, the value pi is −1

.

An example of a tree with n=8

, the root is vertex 5. The parent of the vertex 2 is vertex 3, the parent of the vertex 1 is vertex 5. The ancestors of the vertex 6 are vertices 4 and 5, the ancestors of the vertex 7 are vertices 8, 3 and 5

You noticed that some vertices do not respect others. In particular, if ci=1

, then the vertex i does not respect any of its ancestors, and if ci=0

, it respects all of them.

You decided to delete vertices from the tree one by one. On each step you select such a non-root vertex that it does not respect its parent and none of its children respects it. If there are several such vertices, you select the one with the smallest number. When you delete this vertex v

, all children of v become connected with the parent of v

.

An example of deletion of the vertex 7
.

Once there are no vertices matching the criteria for deletion, you stop the process. Print the order in which you will delete the vertices. Note that this order is unique.

Input

The first line contains a single integer n

(1≤n≤105

) — the number of vertices in the tree.

The next n

lines describe the tree: the i-th line contains two integers pi and ci (1≤pi≤n, 0≤ci≤1), where pi is the parent of the vertex i, and ci=0, if the vertex i respects its parents, and ci=1, if the vertex i does not respect any of its parents. The root of the tree has −1 instead of the parent index, also, ci=0 for the root. It is guaranteed that the values pi define a rooted tree with n

vertices.

Output

In case there is at least one vertex to delete, print the only line containing the indices of the vertices you will delete in the order you delete them. Otherwise print a single integer −1

.

Examples
Input
5
3 1
1 1
-1 0
2 1
3 0
Output
1 2 4
Input
5
-1 0
1 1
1 1
2 0
3 0
Output
-1
Input
8
2 1
-1 0
1 0
1 1
1 1
4 0
5 1
7 0
Output
5
Note

The deletion process in the first example is as follows (see the picture below, the vertices with ci=1

are in yellow):

  • first you will delete the vertex 1
, because it does not respect ancestors and all its children (the vertex 2) do not respect it, and 1
  • is the smallest index among such vertices;
  • the vertex 2
will be connected with the vertex 3
  • after deletion;
  • then you will delete the vertex 2
, because it does not respect ancestors and all its children (the only vertex 4
  • ) do not respect it;
  • the vertex 4
will be connected with the vertex 3
  • ;
  • then you will delete the vertex 4
  • , because it does not respect ancestors and all its children (there are none) do not respect it (vacuous truth);
  • you will just delete the vertex 4
  • ;
  • there are no more vertices to delete.

In the second example you don't need to delete any vertex:

  • vertices 2
and 3
  • have children that respect them;
  • vertices 4
and 5
  • respect ancestors.

In the third example the tree will change this way: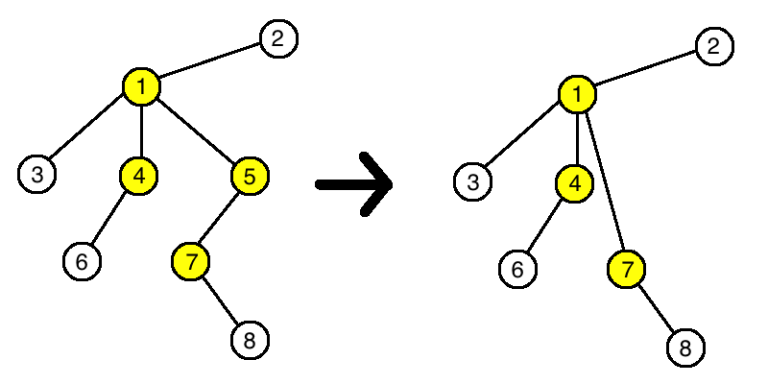

 

题意:输入一个n，接下来n行,每行2个数pi表示第i个结点的父结点,ci为1表示这个结点不尊重他的祖先,为0表示它尊重祖先
对于一个非根结点,如果它不尊重祖先且其孩子不尊重它,则它被删掉且它的孩子连到它的父结点上,输出被删去的结点编号
思路:一开始想如果一个结点被删除就等价于它被它的孩子结点代替,所以如果删除一个结点后就打上删除标记,访问一个被删去的结点时就去访问它的儿子碰到儿子时被删除的结点就递归地访问直到没有一个结点是要被删除的
这样dfs模拟,但这样在test10超时了.其实如果一个结点不尊重祖先,但它的孩子尊重它,则他是不能删的,所以对于一个不尊重祖先但被孩子尊重的结点从它的父结点开始连续的不尊重祖先的结点都是需要删掉的,
所以我们先把不尊重祖先的结点标记,再标记出不尊重祖先但被孩子尊重的结点,最后输出不尊重祖先且不被孩子尊重的结点
注意这里是先标记了不尊重祖先的结点,才看那些是不尊重祖先但被孩子尊重的结点,如果在标记不尊重祖先的结点的同时看那些结点被孩子标记,可能会出现现在这个结点的孩子没被标记为不尊重祖先的结点,但后面的输入是被标记了,这样就错误的把当前这个结点标记为不尊重祖先但被孩子尊重的结点

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<iostream>
 4 #include<queue>
 5 using namespace std;
 6 typedef long long ll;
 7 const int amn=1e5+5;
 8 int n,ans[amn],p[amn],c[amn],root;
 9 int main(){
10     int need[amn];
11     memset(need,0,sizeof need);
12     scanf("%d",&n);
13     for(int i=1;i<=n;i++){
14         scanf("%d%d",&p[i],&c[i]);
15         if(p[i]==-1)root=i;
16         if(c[i])need[i]=1;
17     }
18     for(int i=1;i<=n;i++){
19         if(!c[i])need[p[i]]=0;
20     }
21     int tp=0;
22     for(int i=1;i<=n;i++){
23         if(!need[i]||i==root)continue;
24         if(c[i]&&need[i])
25             ans[++tp]=i;
26     }
27     if(tp){
28         for(int i=1;i<=tp;i++)printf("%d%c",ans[i],i<tp?' ':'\n');
29     }
30     else printf("-1\n");
31 }
32 /**
33 题意:输入一个n，接下来n行,每行2个数pi表示第i个结点的父结点,ci为1表示这个结点不尊重他的祖先,为0表示它尊重祖先
34 对于一个非根结点,如果它不尊重祖先且其孩子不尊重它,则它被删掉且它的孩子连到它的父结点上,输出被删去的结点编号
35 思路:一开始想如果一个结点被删除就等价于它被它的孩子结点代替,所以如果删除一个结点后就打上删除标记,访问一个被删去的结点时就去访问它的儿子碰到儿子时被删除的结点就递归地访问直到没有一个结点是要被删除的
36 这样dfs模拟,但这样在test10超时了.其实如果一个结点不尊重祖先,但它的孩子尊重它,则他是不能删的,所以对于一个不尊重祖先但被孩子尊重的结点从它的父结点开始连续的不尊重祖先的结点都是需要删掉的,
37 所以我们先把不尊重祖先的结点标记,再标记出不尊重祖先但被孩子尊重的结点,最后输出不尊重祖先且不被孩子尊重的结点
38 注意这里是先标记了不尊重祖先的结点,才看那些是不尊重祖先但被孩子尊重的结点,如果在标记不尊重祖先的结点的同时看那些结点被孩子标记,可能会出现现在这个结点的孩子没被标记为不尊重祖先的结点,但后面的输入是被标记了,这样就错误的把当前这个结点标记为不尊重祖先但被孩子尊重的结点
39 **/

 

 

posted @ 2019-11-09 20:00  Railgun000  阅读(164)  评论(0)  编辑  收藏  举报