01 绪论 | 常微分方程

1. 微分方程的定义

1. 微分方程：联系自变量，未知函数以及 未知函数的导数的关系式称为 微分方程
   1. 常微分方程：在一个微分方程中，自变量只有一个
   2. 偏微分方程：在一个微分方程中，自变量有两个或以上
2. 阶数：微分方程中出现的未知函数的 最高阶导数或微分的阶数 称为微分方程的 阶数
3. $n$阶微分方程的一般形式：$F(x,y,\frac{dy}{dx},\cdots ,\frac{d^{n}y}{d{x}^n})=0$，其中$y$是未知函数，$x$是自变量
   1. 线性微分方程：如果上述方程的左端为$y,\frac{dy}{dx},\cdots ,\frac{d^{n}y}{d{x}^n}$的 一次有理式，则称为 线性微分方程
   2. 非线性微分方程：不是线性微分方程的微分方程

2. 微分方程的解和通解

1. 微分方程的解：如果函数$y=\phi (x),x\in I$，满足条件：
   1. $y=\phi (x)$在$I$上有直到$n$阶的连续导数
   2. 对$\mathrm{\forall }x\in I$有：$F(x,\phi (x),\cdots ,{\phi }^n(x))\equiv 0$
      则称$y=\phi (x)$为方程$F(x,y,\frac{dy}{dx},\cdots ,\frac{d^{n}y}{d{x}^n})=0$在$I$上的一个解
2. 显式解：$y=\phi (x)$
3. 隐式解：如果关系式$\mathrm{\Phi }(x,y)=0$所确定的隐函数$y=\phi (x),x\in I$为方程$F(x,y,\frac{dy}{dx},\cdots ,\frac{d^{n}y}{d{x}^n})=0$的解，则称$\mathrm{\Phi }(x,y)=0$是方程的一个 隐式解
4. 通解：如果微分方程的解中含有任意常数，且所含的 相互独立 的任意常数的个数与微分方程的阶数 相同，则称这样的解为该方程的 通解
   1. $n$阶微分方程的通解的一般形式为$y=\phi (x,c_1,\cdots ,c_n)$，其中$c_1,\cdots ,c_n$为相互独立的任意常数
   2. 相互独立：存在$(x,c_1,\cdots ,c_n)$的某一个邻域，使得行列式
      $$\frac{\partial (\phi ,\cdots ,{\phi }^{(n-1)})}{\partial (c_1,\cdots ,c_n)}=\left|\begin{array}{cccc}\frac{\partial \phi }{\partial c_1}& \frac{\partial \phi }{\partial c_2}& \cdots & \frac{\partial \phi }{\partial c_n}\\ \frac{\partial {\phi }^{\prime }}{\partial c_1}& \frac{\partial {\phi }^{\prime }}{\partial c_2}& \cdots & \frac{\partial {\phi }^{\prime }}{\partial c_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial {\phi }^{(n-1)}}{\partial c_1}& \frac{\partial {\phi }^{(n-1)}}{\partial c_2}& \cdots & \frac{\partial {\phi }^{(n-1)}}{\partial c_n}\end{array}\right|\ne 0$$

   3. 独立常数个数与方程阶数 相同
   4. 不是所有微分方程都有通解
   5. 微分方程的通解不包含方程的所有解
   6. 微分方程在不同区域内的通解形式可能不同

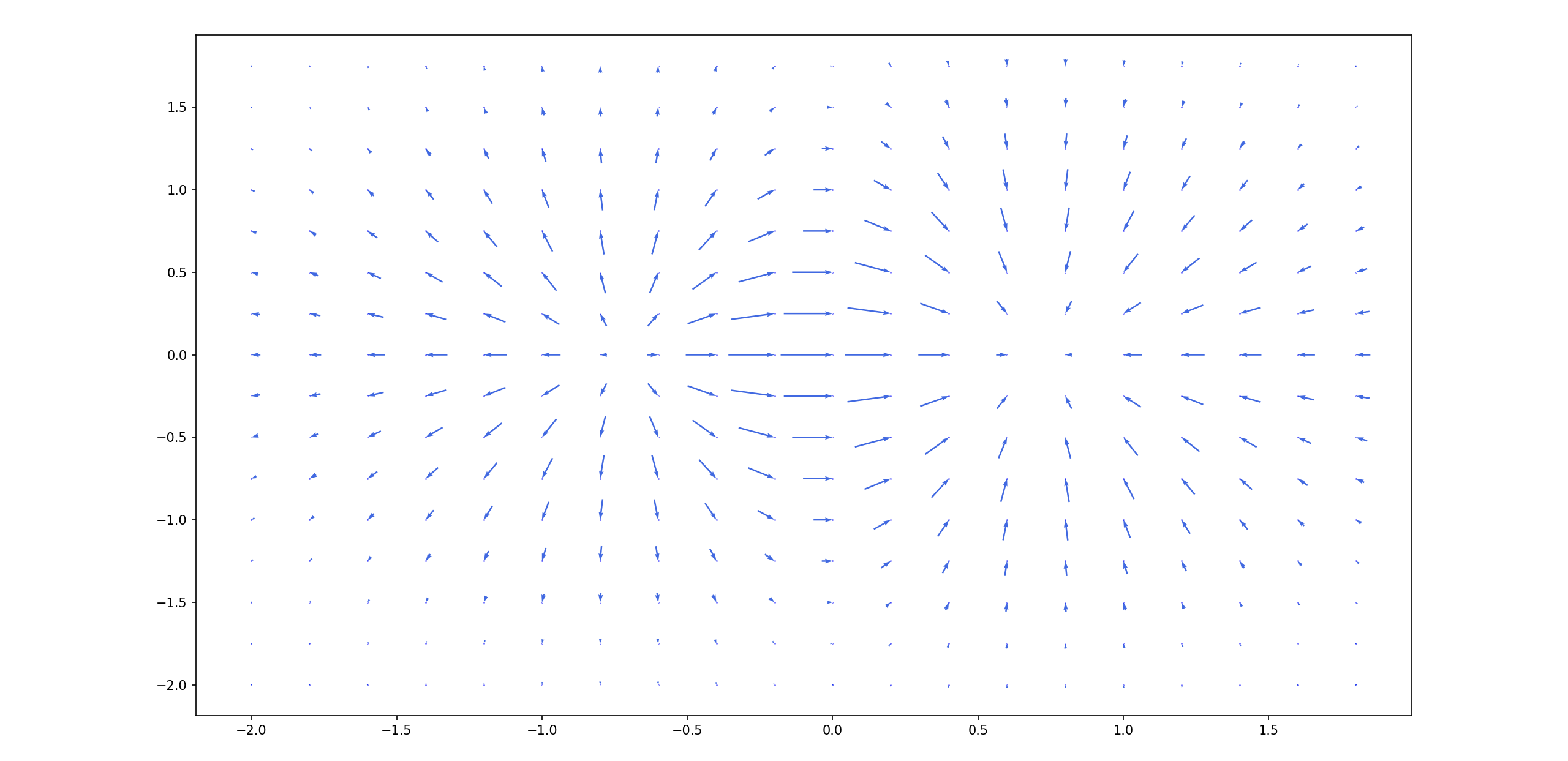
3. 微分方程的积分曲线和向量场

1. 积分曲线：一阶微分方程$\frac{dy}{dx}=f(x,y)$的一个解$y=\phi (x)$所表示$xy$平面上的一条曲线称为微分方程的 积分曲线

2. 积分曲线族：其通解$y=\phi (x,c)$对应$xy$平面上的一族曲线（每一个$c$都对应一条曲线），称为这族曲线为微分方程的 积分曲线族

3. 方向场：设函数$f(x,y)$的定义域为$D$，在$D$内每一点$(x,y)$处都画一个以$f(x,y)$的值为斜率，中心在$(x,y)$点的线段，称带有这种线段（该线段称为线素）的区域$D$ 为微分方程 $\frac{dy}{dx}$所确定的 方向场

4. 等倾斜线：在方向场中，方向相同的点的几何轨迹称为 等倾斜线

5. 方程组积分曲线：设方程组$\frac{dY}{dt}=F(t,Y),Y=(y_1,\dots ,y_n{)}^T$，其解为

   $$\{\begin{array}{c}{y}_1={\phi }_1(t)\\ ⋮\\ y_n={\phi }_n(t)\end{array}$$

   是一参数方程，积分曲线是点$(t,{\phi }_1(t),\dots ,{\phi }_n(t))$的轨迹，注意这里的$t$是坐标分量

4. 驻定与非驻定

1. 驻定（自治）：如果方程组右端不含自变量 $t$：$\frac{dY}{dt}=F(Y),Y\in D\subseteq R^n$
2. 非驻定（非自治）：如果方程组右端含自变量 $t$
3. 非驻定可化为驻定方程组：令$t=\tau$，转为
   $$\{\begin{array}{c}\frac{dY}{d\tau }=F(t,Y),Y\in D\subseteq R^n\\ \frac{dt}{d\tau }=1\end{array}$$

5. 微分方程所定义的动力系统

1. 动力系统：对$n$维空间某区域$D\subseteq R^n$ ，$D$到$D$的含参数$t$的同胚映射(变换)${\mathrm{\Phi }}_t(Y)$，如满足恒同性${\mathrm{\Phi }}_0(Y)=Y$和可加性${\mathrm{\Phi }}_{t_1+t_2}(Y)={\mathrm{\Phi }}_{t_1}({\mathrm{\Phi }}_{t_2}(Y))={\mathrm{\Phi }}_{t_2}({\mathrm{\Phi }}_{t_1}(Y))$ ，称映射${\mathrm{\Phi }}_t(Y)$为$D$ 上的 动力系统
2. 由驻定微分方程组过$Y\in D\subseteq R^n$的解$\phi (t,Y)=0$可定义动力系统${\mathrm{\Phi }}_t(Y)=\phi (𝑡,𝑌)$，称为微分方程所定义的动力系统

__EOF__

本文作者：RadiumGalaxy
本文链接：https://www.cnblogs.com/RadiumGalaxy/p/17235199.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！