10 排序 | 数据结构与算法
1. 排序概述
1. 排序的概念
- 排序:将一组杂乱无章的数据排列成一个按关键字有序的序列
- 数据表:待排序数据对象的有限集合
- 关键字:通常数据对象有多个属性域,即多个数据成员组成,其中有一个属性域可用来区分对象,作为排序依据。该域即为 关键字 。每个数据表用哪个属性域作为关键字,要视具体的应用需要而定。即使是同一个表,在解决不同问题的场合也可能取不同的域做关键字
2. 排序算法的稳定性
- 如果在对象序列中有两个对象
r[i]和r[j],它们的关键字k[i] == k[j],且在排序之前,对象r[i]排在r[j]前面。如果在排序之后,对象r[i]仍在对象r[j]的前面,则称这个排序方法是 稳定的,否则称这个排序方法是不稳定的
3. 内排序和外排序
- 内排序:在排序期间数据对象全部存放在内存的排序
- 外排序:在排序期间全部对象个数太多,不能同时存放在内存,必须根据排序过程的要求,不断在内、外存之间移动的排序
4. 排序的时间开销
- 排序的时间开销是衡量算法好坏的最重要的标志。排序的时间开销可用算法执行中的数据比较次数与数据移动次数来衡量
- 各节给出算法运行时间代价的大略估算一般都按平均情况进行估算
- 对于那些受对象关键字序列初始排列及对象个数影响较大的,需要按最好情况和最坏情况进行估算
5. 衡量排序方法的标准
- 排序时所需要的平均比较次数
- 排序时所需要的平均移动次数
- 排序时所需要的平均辅助存储空间
- 排序的稳定性
2. 排序的分类
1. 插入排序
-
原理:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
-
算法分析
- 时间复杂度
- 关键字比较次数和对象移动次数与对象关键字的初始排列有关
- 最好情况下:排序前对象已经按关键字大小从小到大有序,每趟只需与前面的有序对象序列的最后一个对象的关键字比较
- 时间复杂度
-
算法
2. 希尔排序
-
原理: 先将整个待排对象序列按照一定间隔分割成为若干子序列,分别进行直接插入排序,然后缩小间隔,对整个对象序列重复以上的划分子序列和分别排序工作,直到最后间隔为1,此时整个对象序列已 “基本有序”,进行最后一次直接插入排序
-
算法分析
- 希尔排序是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法
- 希尔排序是基于插入排序的以下两点性质而提出改进方法的
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
gap的取法:最初
-
算法
-
冒泡排序
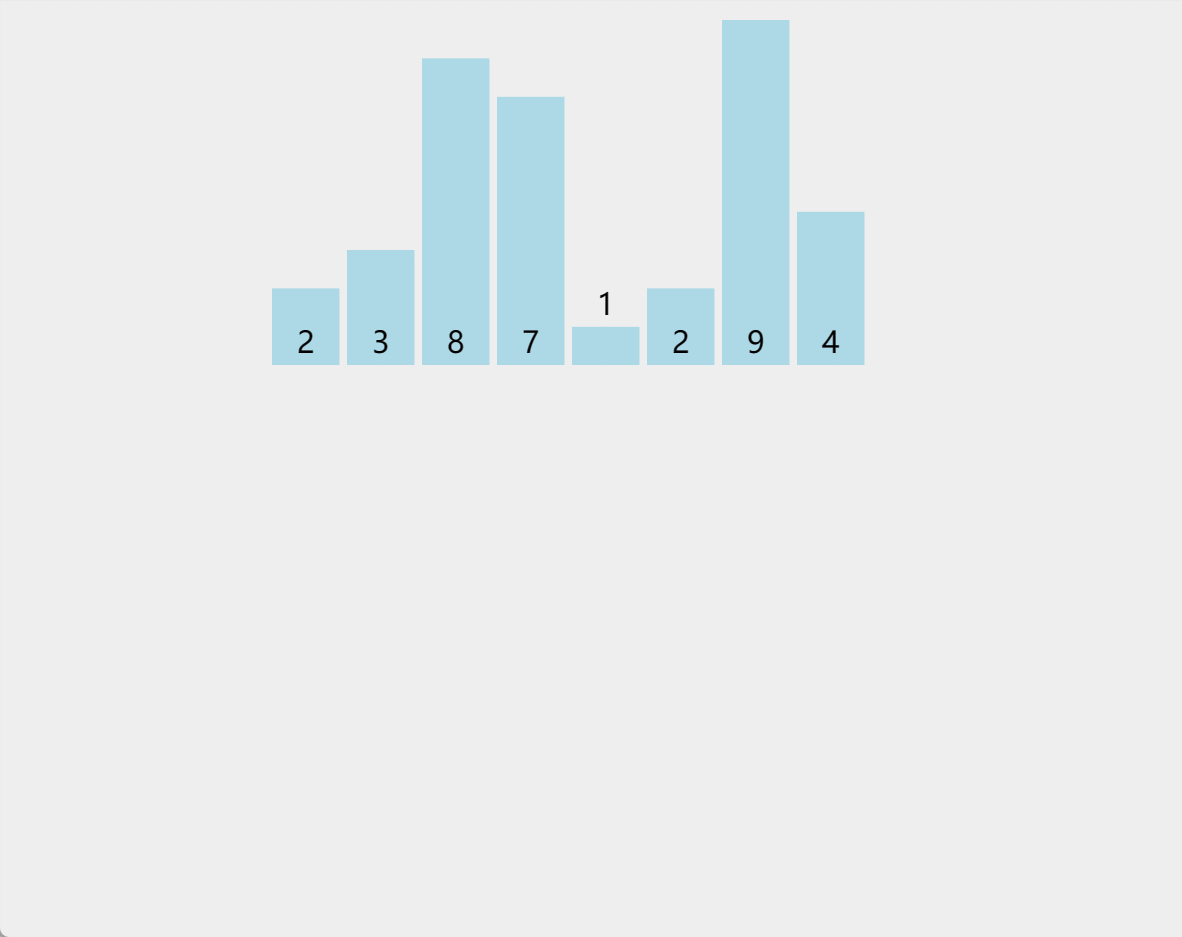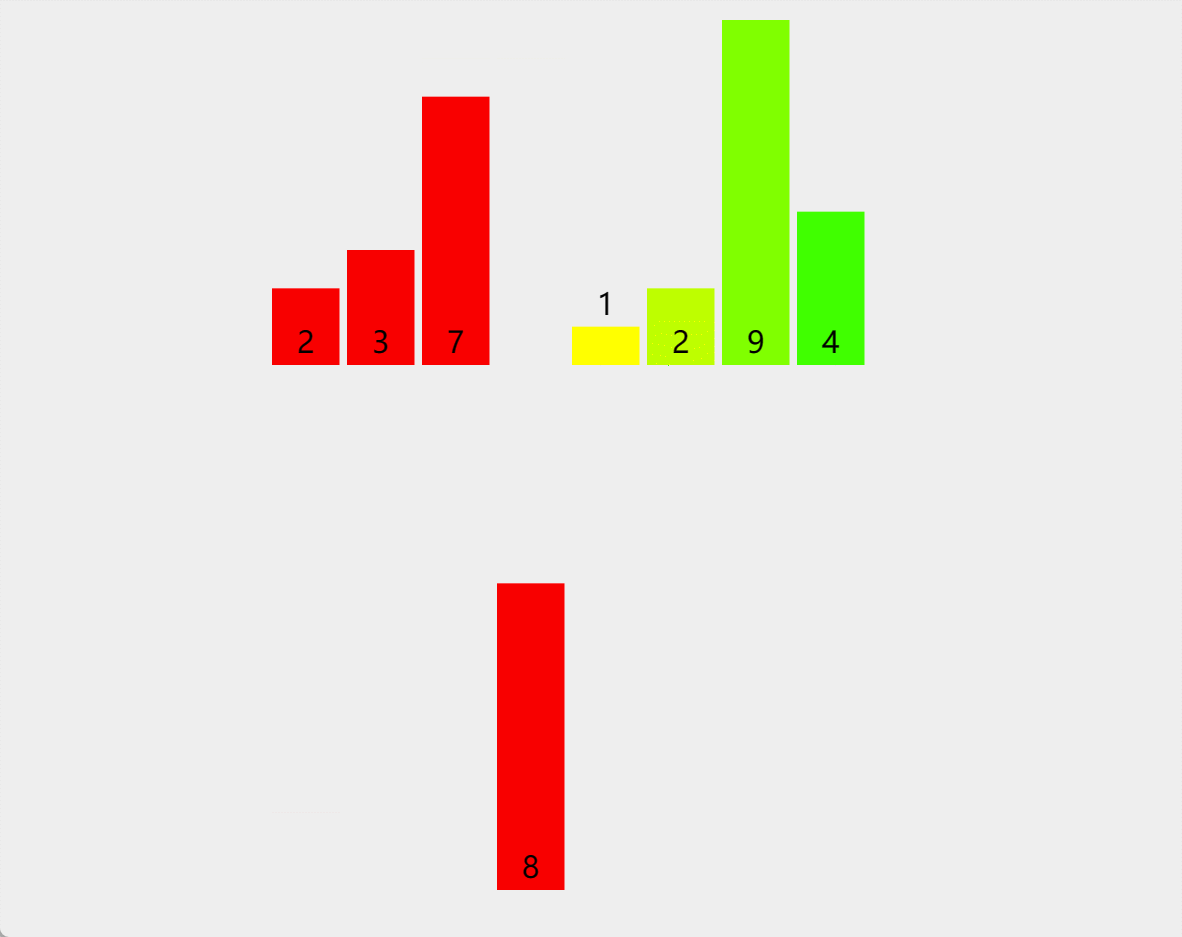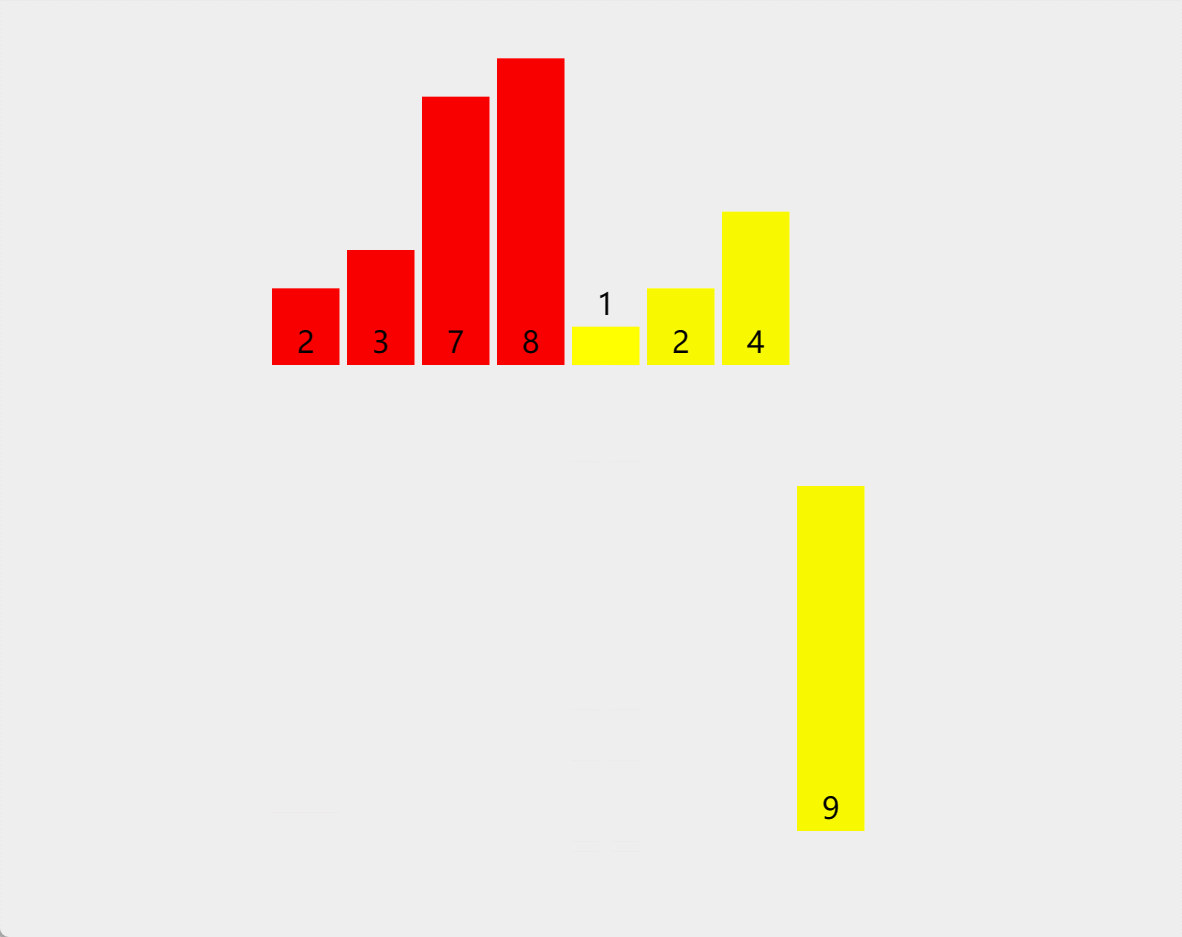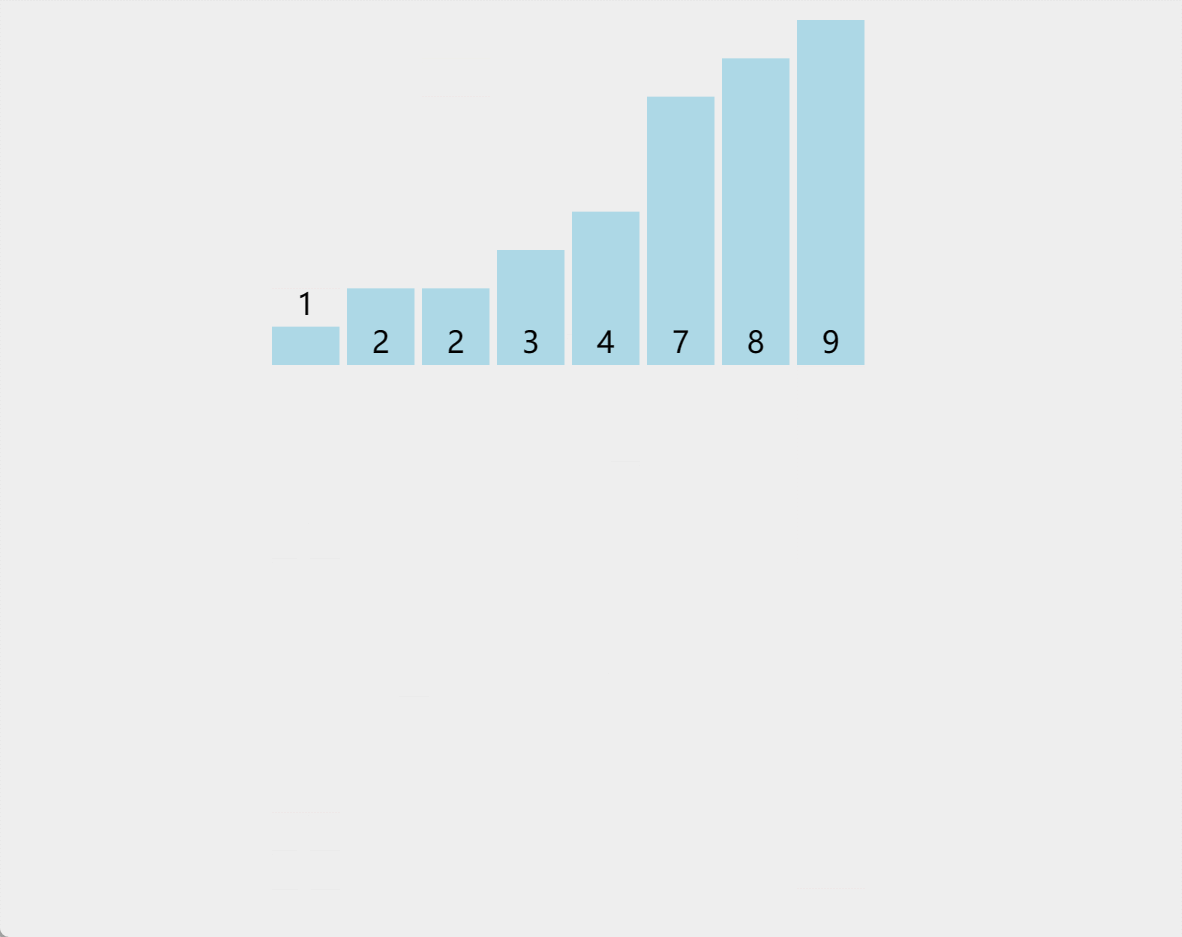
4. 快速排序
-
原理:任取待排序对象序列中的某个对象 (例如取第一个对象) 作为枢轴(
pivot),按照该对象的关键字大小,将整个对象序列划分为左右两个子序列; 左侧子序列中所有对象的关键字都小于或等于枢轴对象的关键字;右侧子序列中所有对象的关键字都大于枢轴对象的关键字,对左右两个序列重复以上过程 -
算法分析
- 平均时间复杂度
- 快速排序是一个 不稳定 的排序算法
- 从快速排序算法的递归树可知,快速排序的趟数取决于递归树的深度;如果每次划分对一个对象定位后,该对象的左侧子序列与右侧子序列的长度相同,则下一步将是对两个长度减半的子序列进行排序,这是最理想的情况
- 最坏情况会退化到
- 空间复杂度:递归栈的深度,最好
- 平均时间复杂度
-
算法
5. 选择排序
-
原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置;再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾;重复以上步骤,直到所有元素均排序完毕
-
算法分析
- 总的比较次数:
- 对象的移动次数与对象序列的初始排列有关。当这组对象的初始状态是按其关键字从小到大有序的时候,对象的移动次数为 0,达到最少
- 直接选择排序是一种不稳定的排序方法
- 时间复杂度
- 总的比较次数:
-
算法
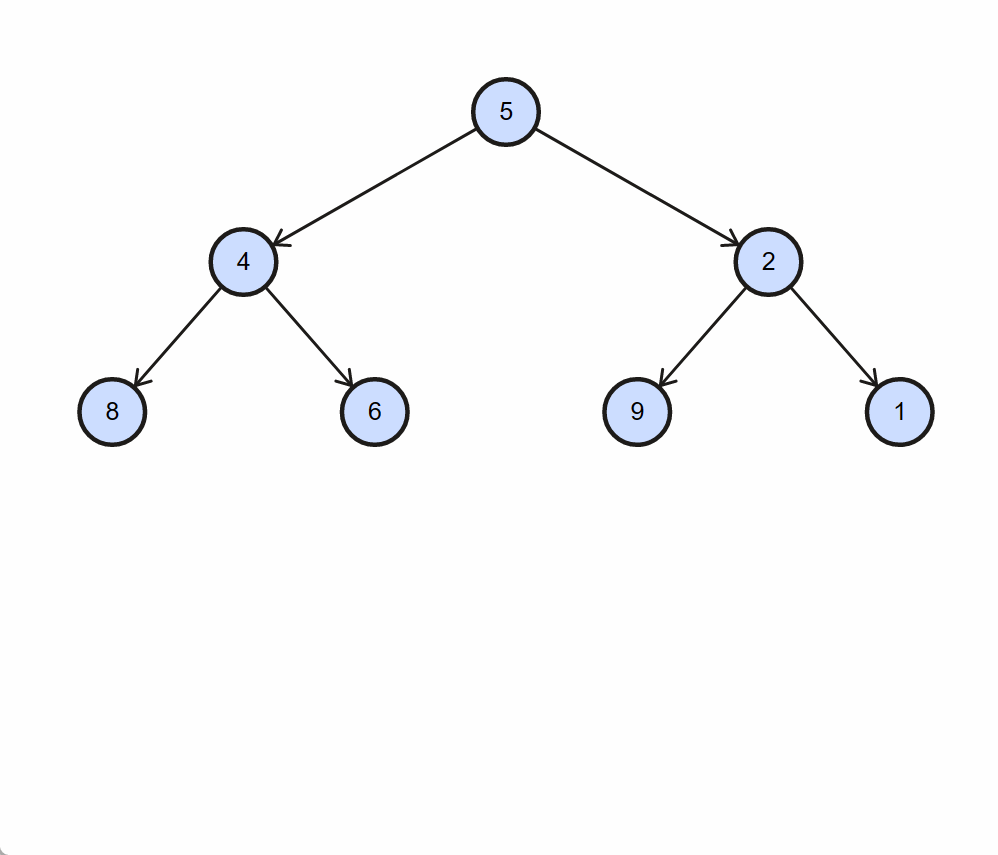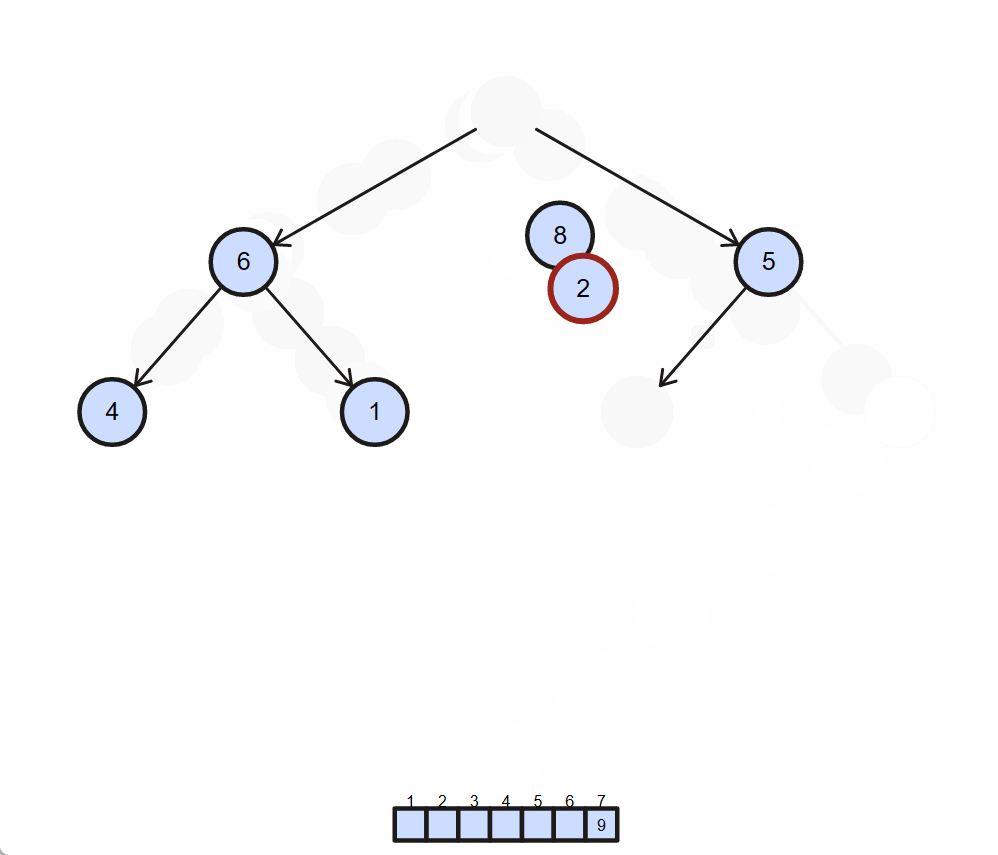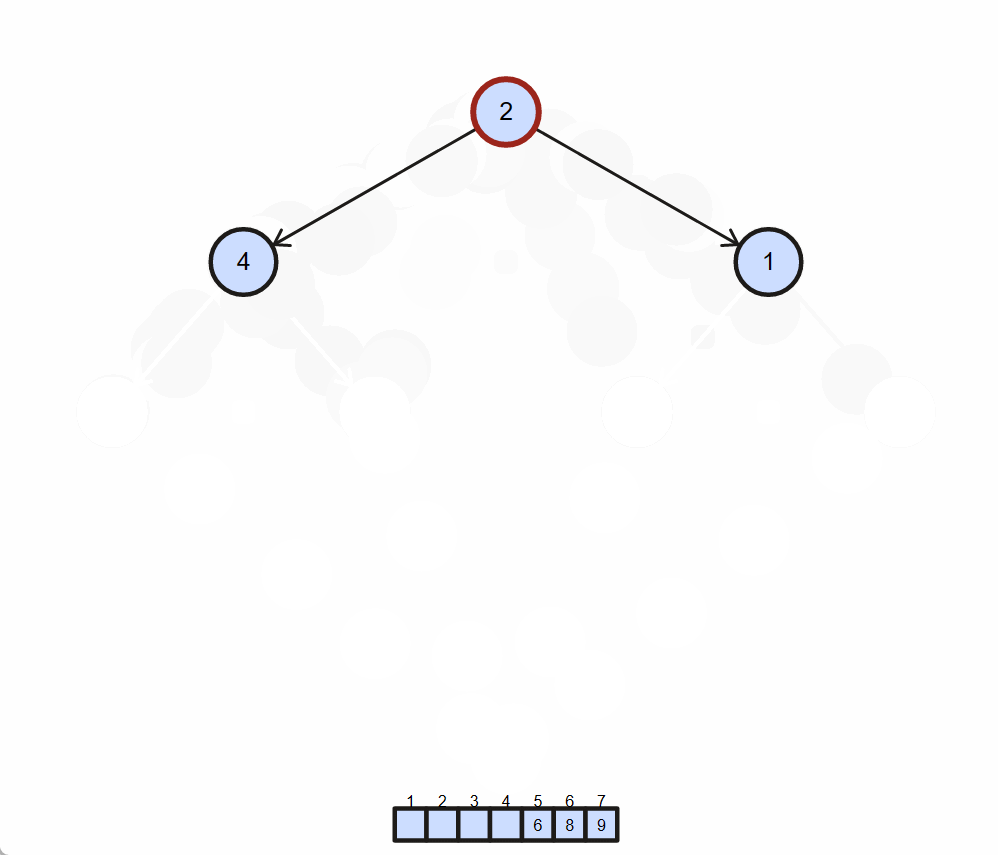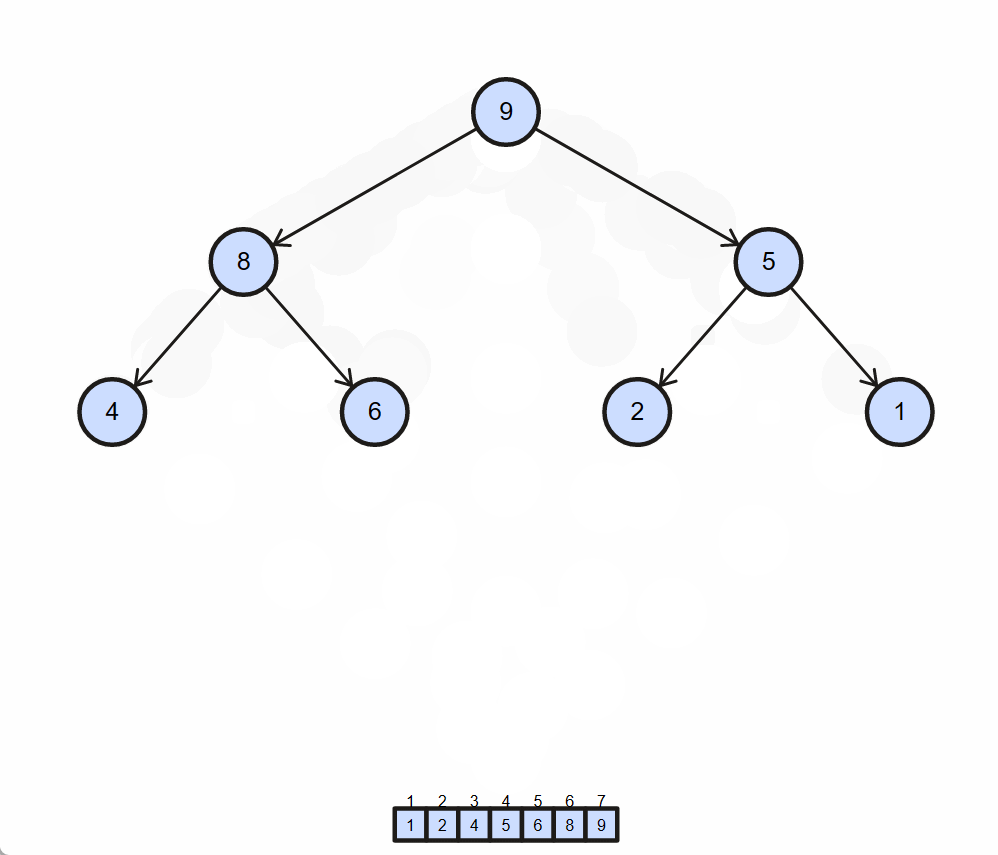
6. 堆排序
-
原理:利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法
- 大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列
- 小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列
-
算法步骤(以小顶堆为例)
- 创建一个堆
H[0:n-1]:对于index = m / 2到index = 0的元素进行筛选- 如果
- 如果
- 如果
- 如果
- 如果
- 把堆首(最大值)和堆尾互换
- 把堆的尺寸缩小 1,把新的数组顶端数据调整到相应位置
- 重复步骤2,直到堆的尺寸为 1
- 创建一个堆
-
算法分析
- 时间复杂度
- 堆排序是 不稳定 的排序算法
- 时间复杂度
-
算法
7. 归并排序
-
原理:归并,是将两个或两个以上的有序表合并成一个新的有序表的过程。归并排序的主要操作是归并,其主要思想是:将若干有序序列逐步归并,最终得到一个有序序列
-
算法步骤(二路归并)
- 初始时,将每个记录看成一个单独的有序序列,则
- 对所有有序子序列进行两两归并,得到长度为
- 重复步骤2,直到得到长度为
- 初始时,将每个记录看成一个单独的有序序列,则
-
算法分析
- 时间复杂度
- 空间复杂度
- 归并排序是一个稳定的排序方法
- 时间复杂度
-
算法
8. 基数排序
-
原理:基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数
-
算法分析
- 若每个关键字有
- 基数排序是稳定的排序方法
- 基数排序的适用范围:要求关键字分量的取值范围必须是有限的
- 若每个关键字有
-
算法
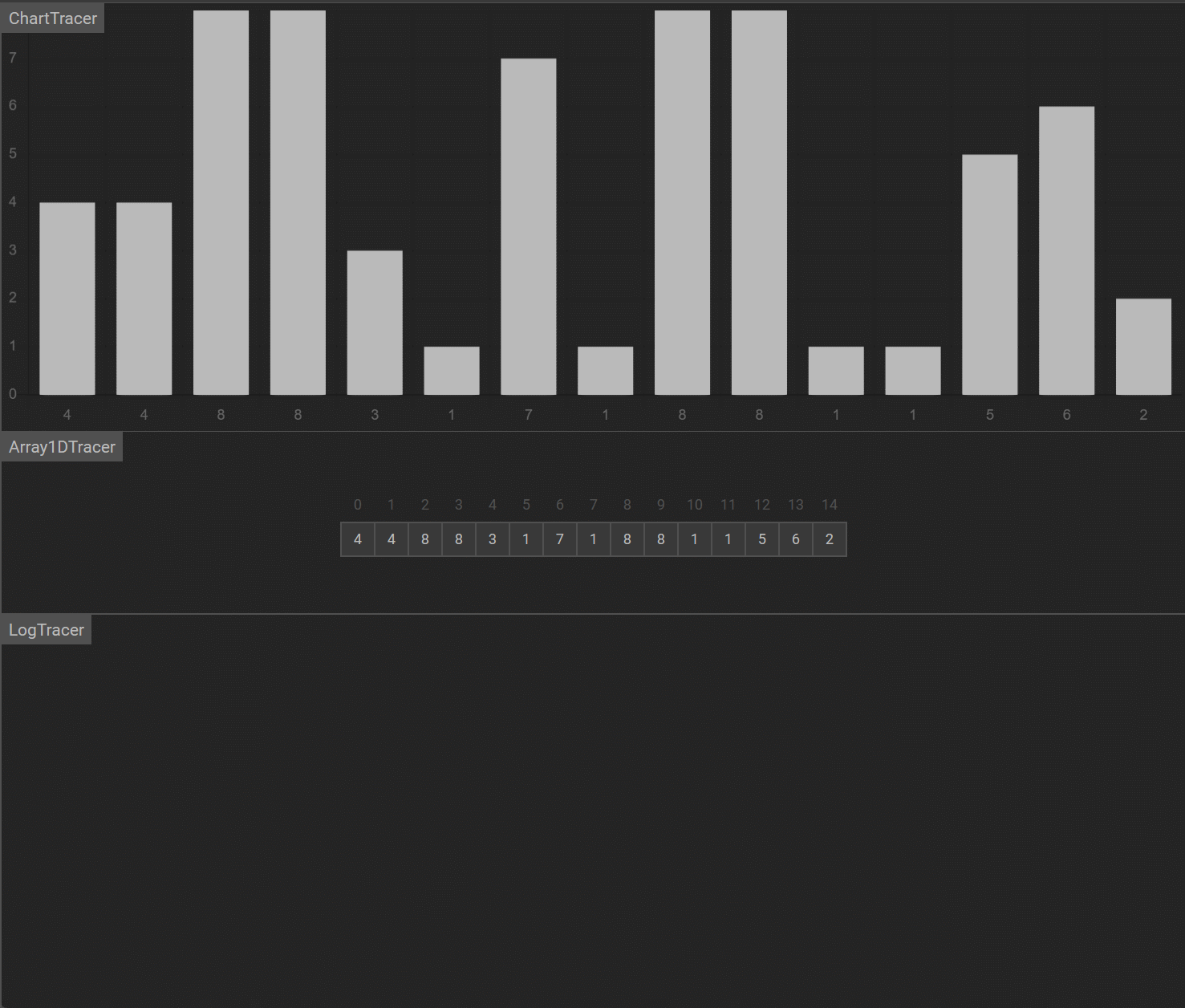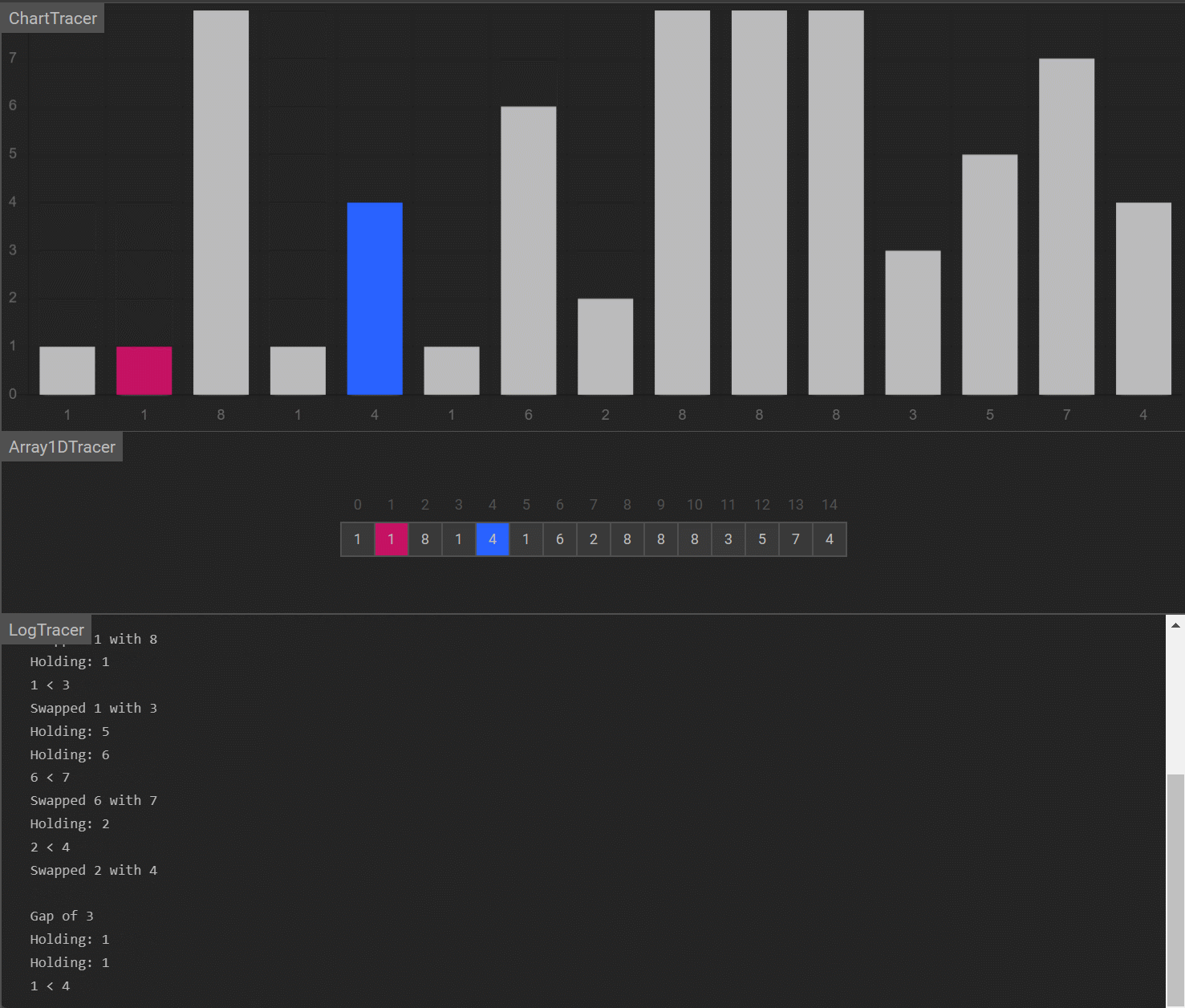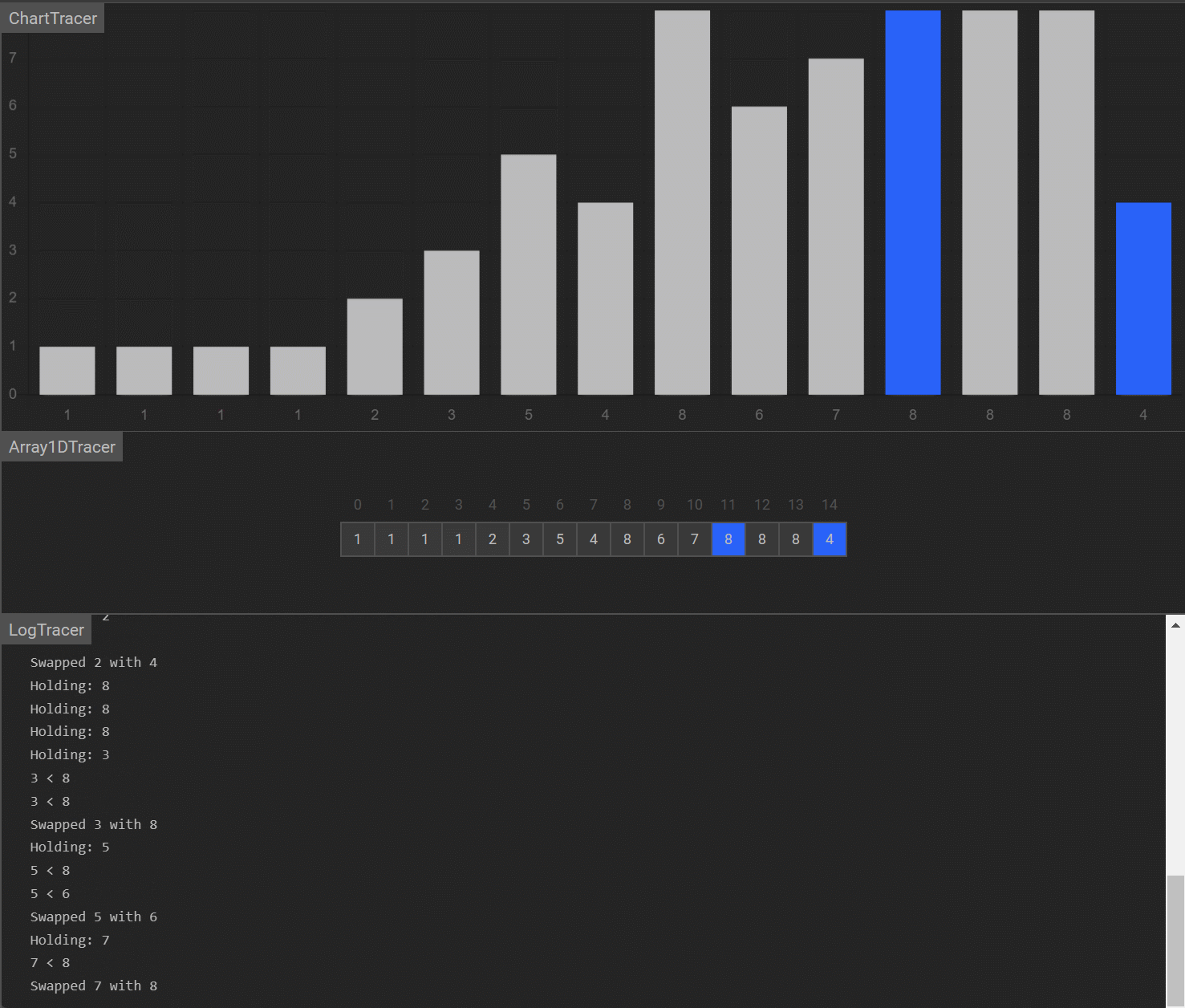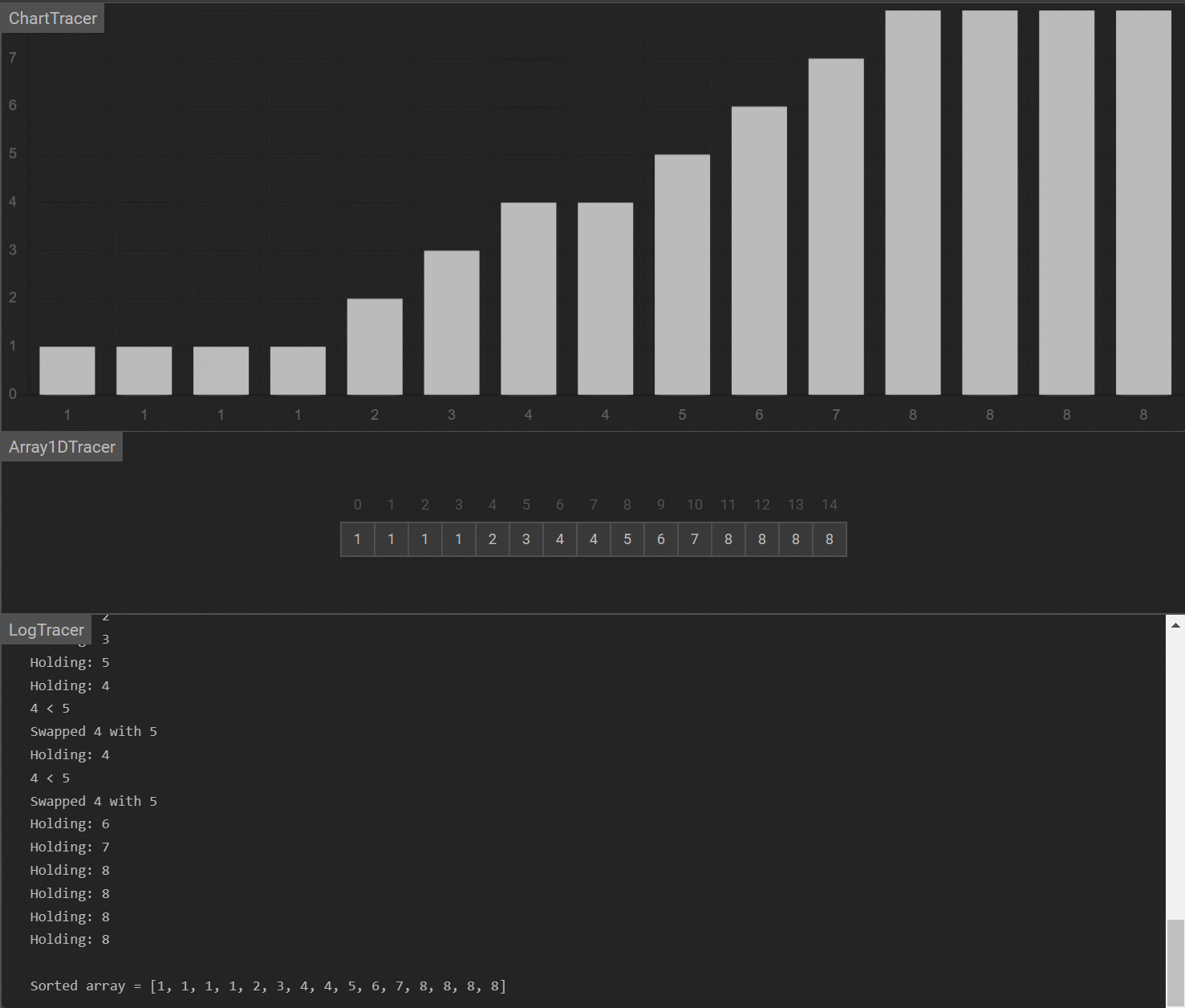
9. 排序比较
sort |
比较次数 | 移动次数 | 稳定性 | 附加存储 |
|---|---|---|---|---|
| 插入排序 | 最好: |
最好: |
✔️ | |
| 冒泡排序 | 最好: |
最好: |
✔️ | |
| 快速排序 | 最好: |
最好: |
❌ | 最好: |
| 选择排序 | 最好: |
❌ | ||
| 堆排序 | ❌ | |||
| 归并排序 | ✔️ |
__EOF__
本文链接:https://www.cnblogs.com/RadiumGalaxy/p/17069489.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!

 排序算法
排序算法
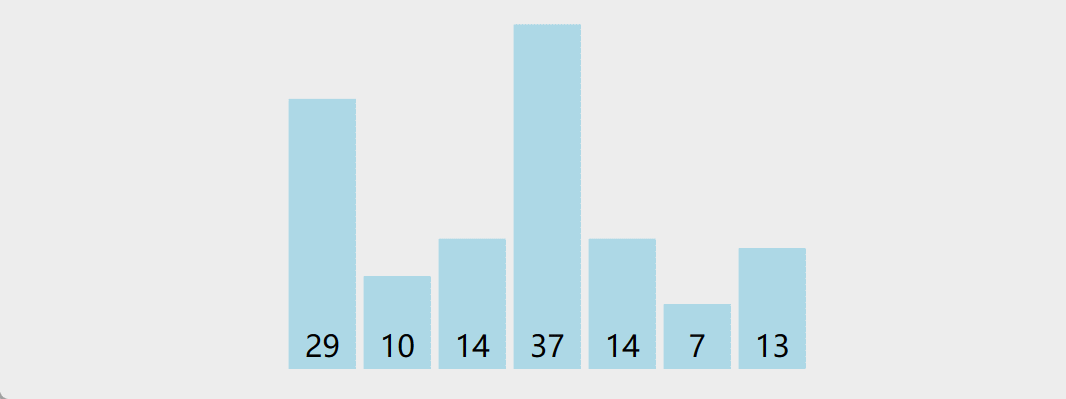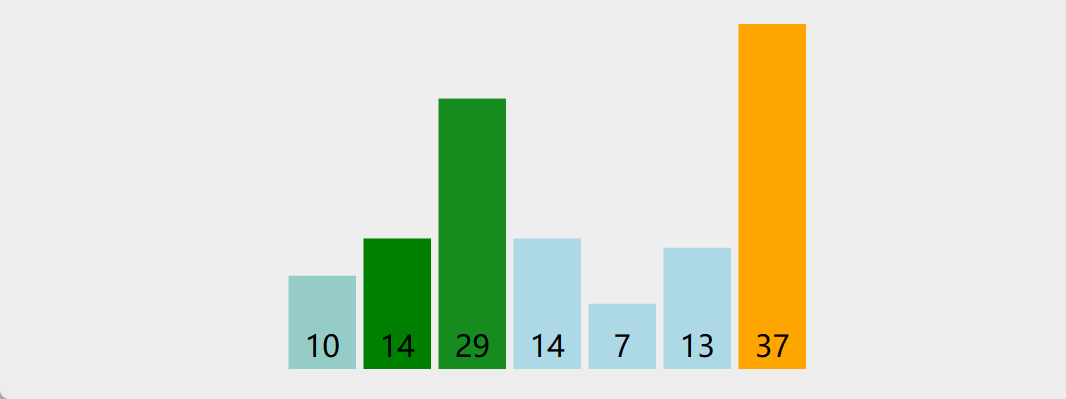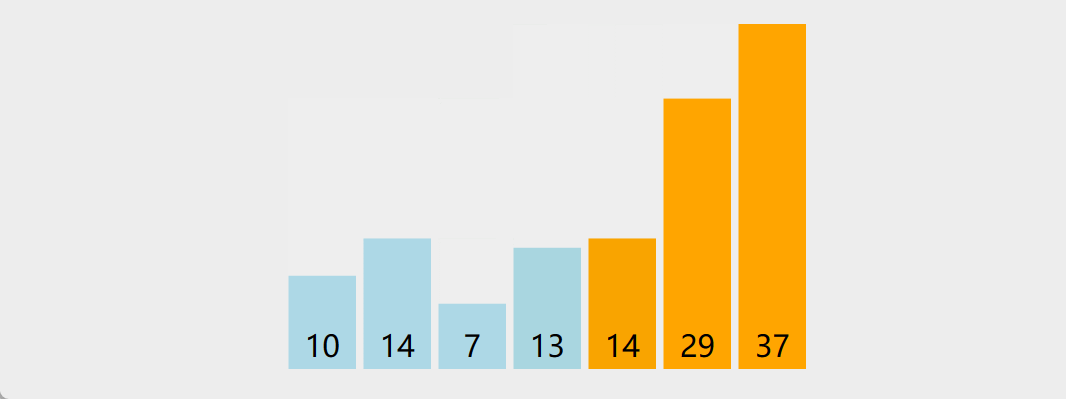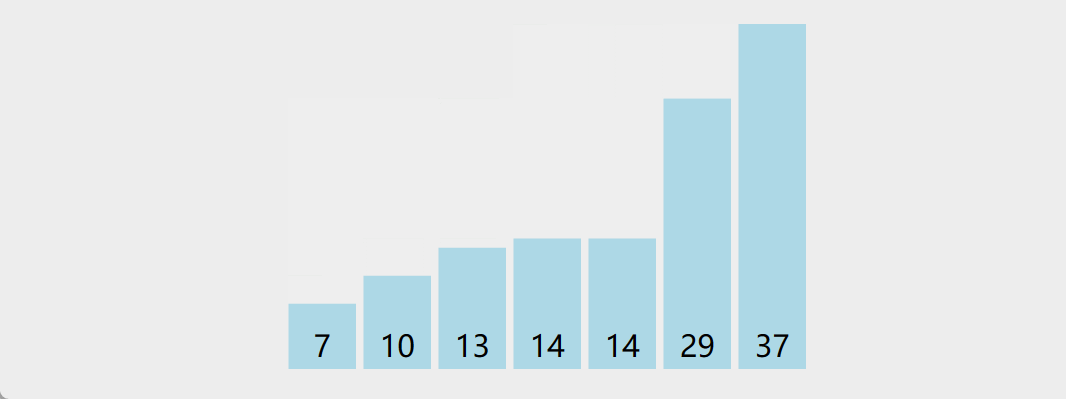
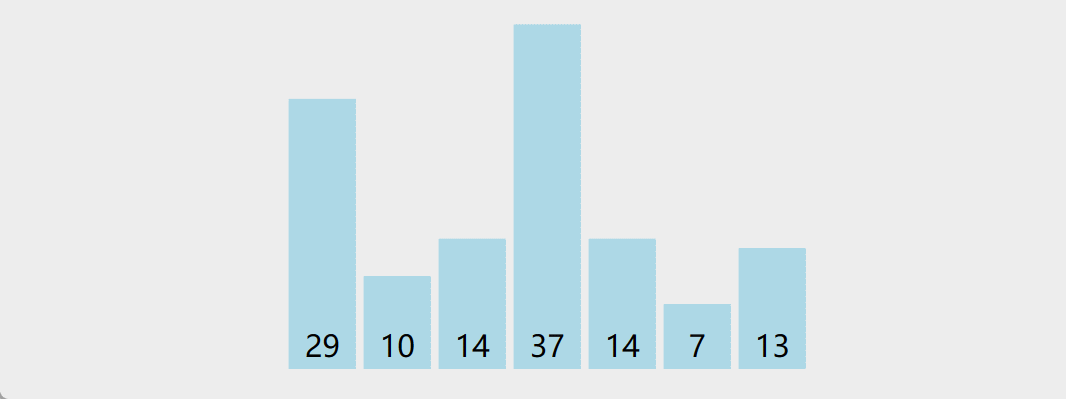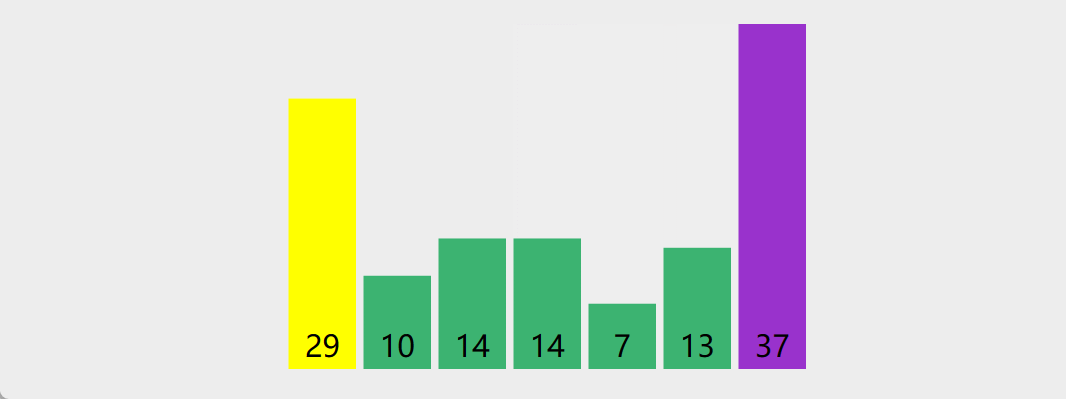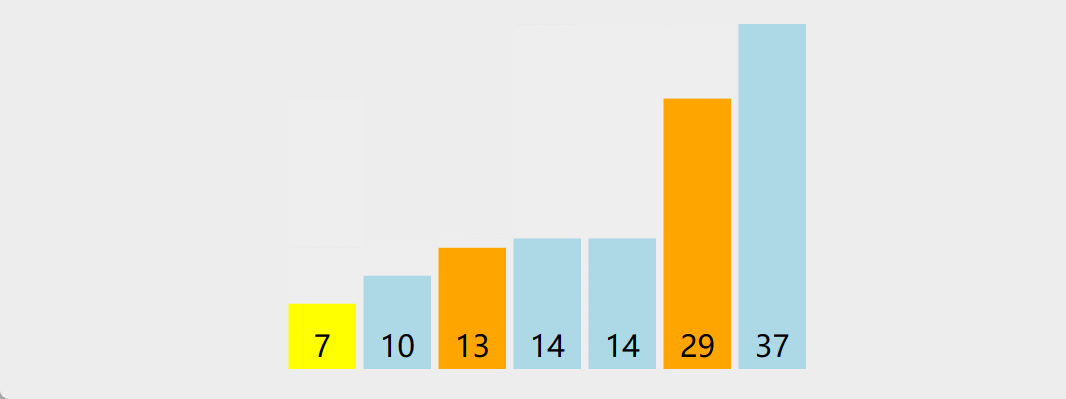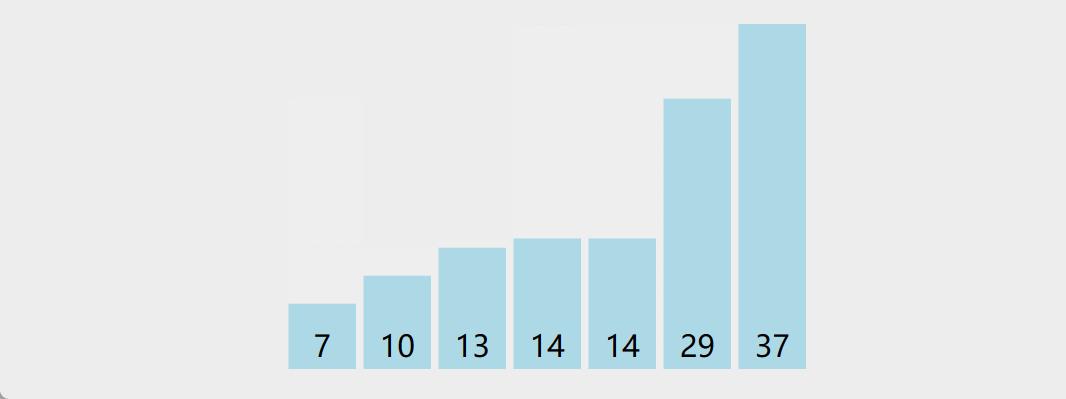
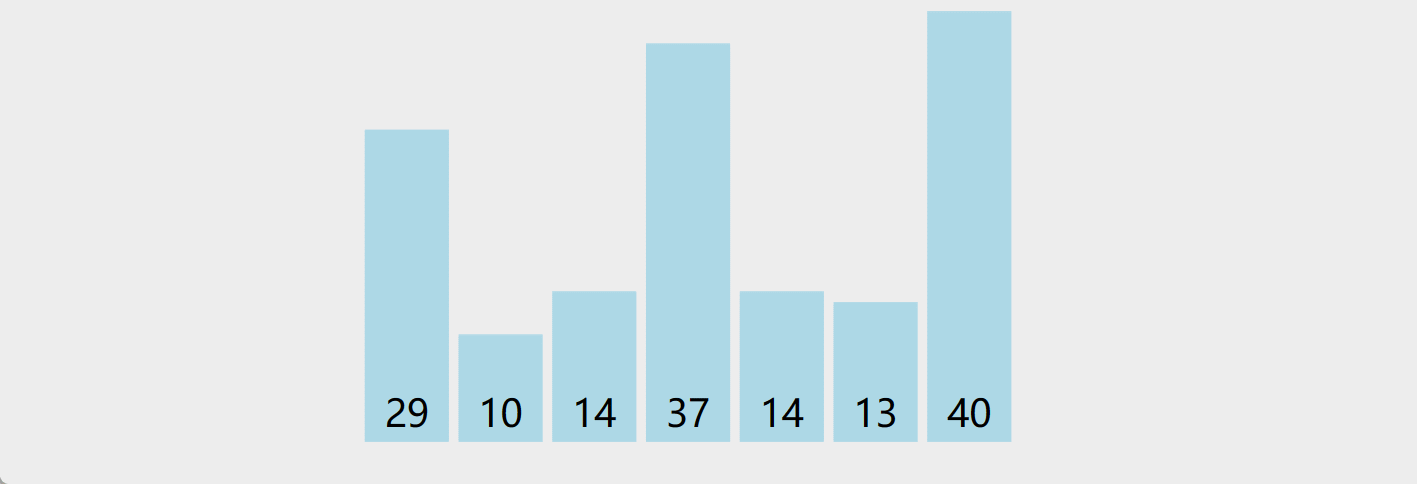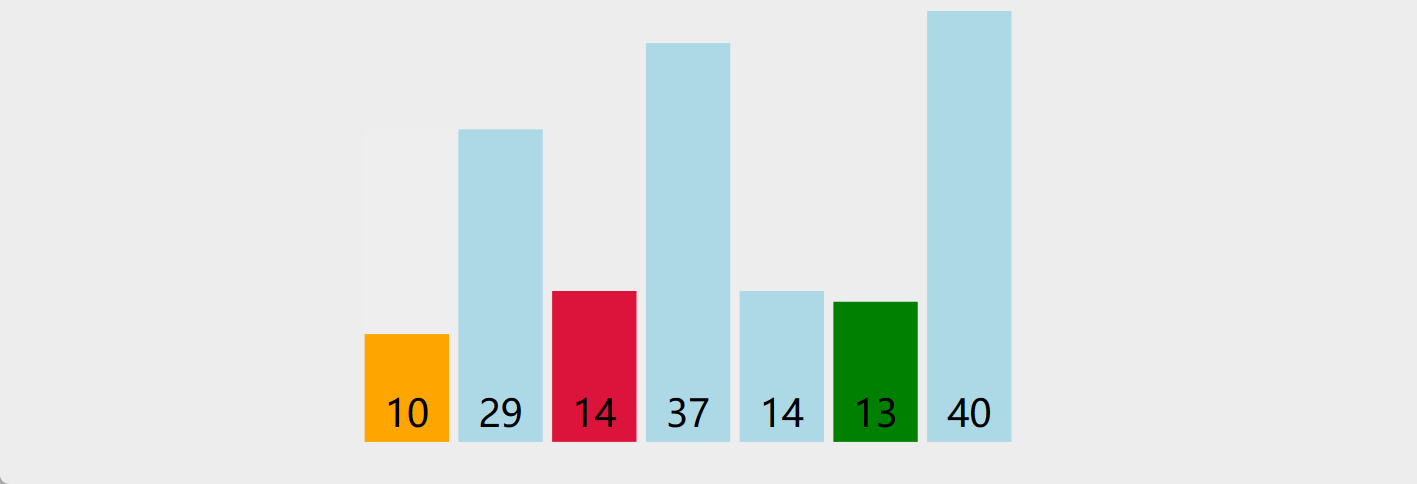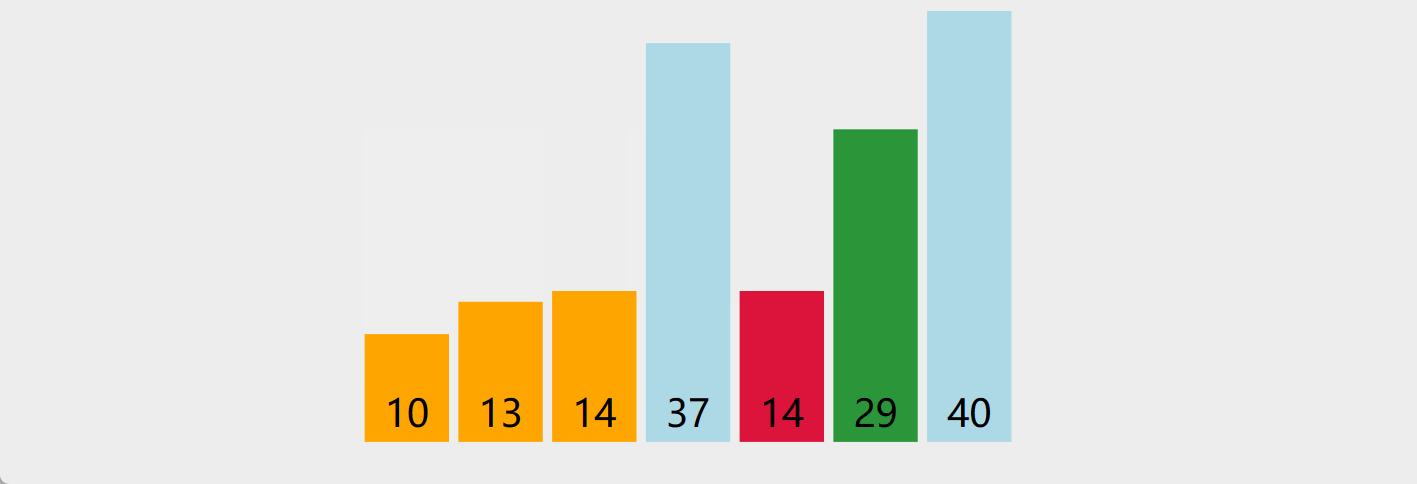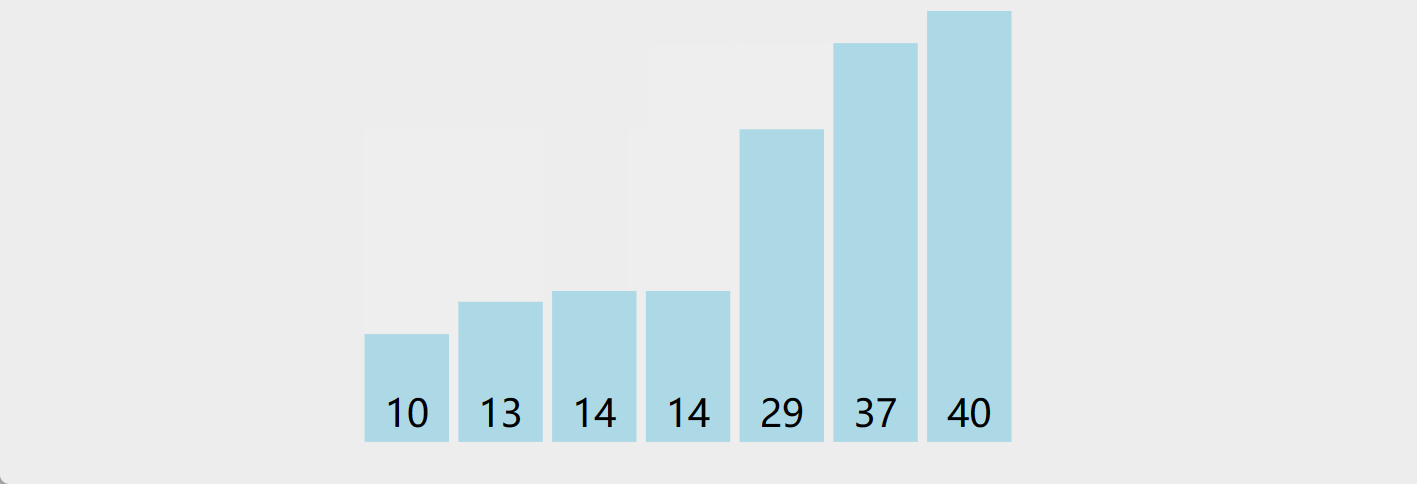
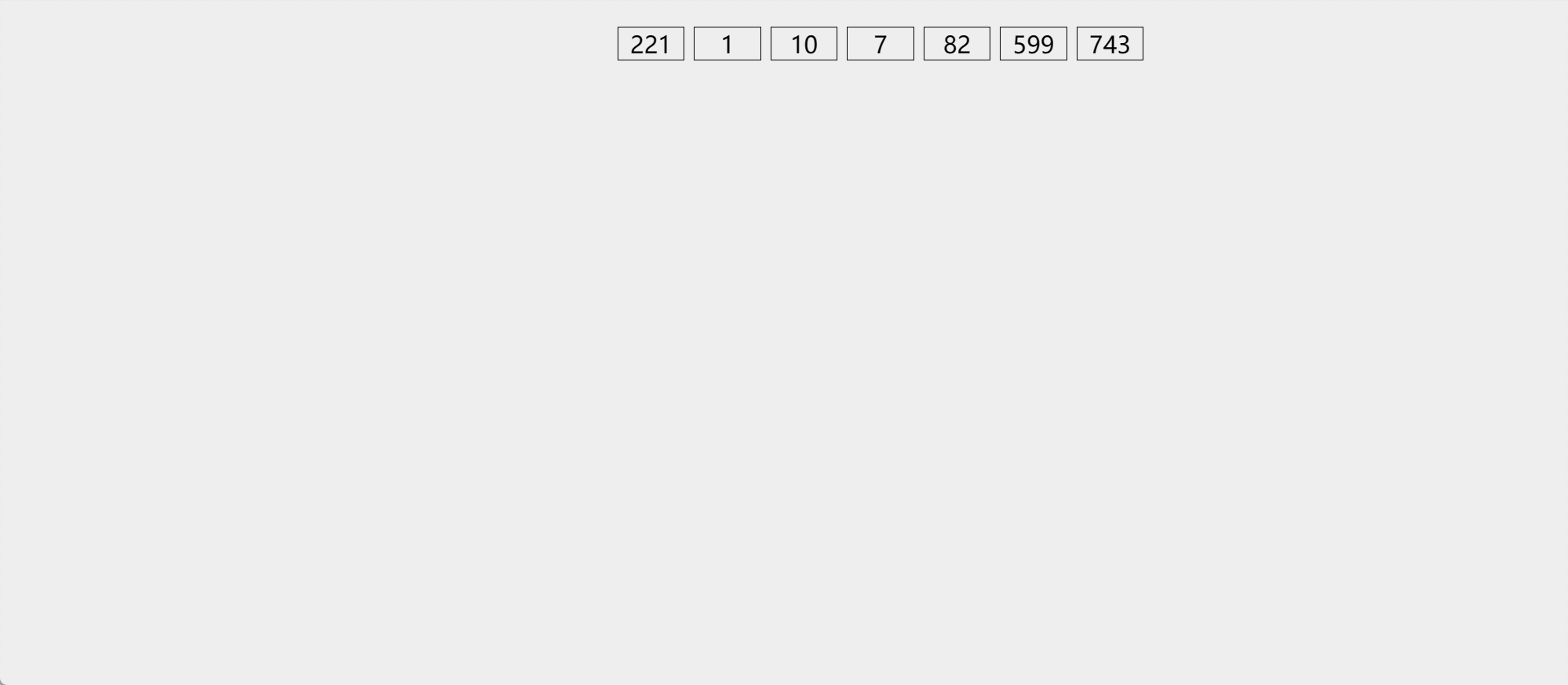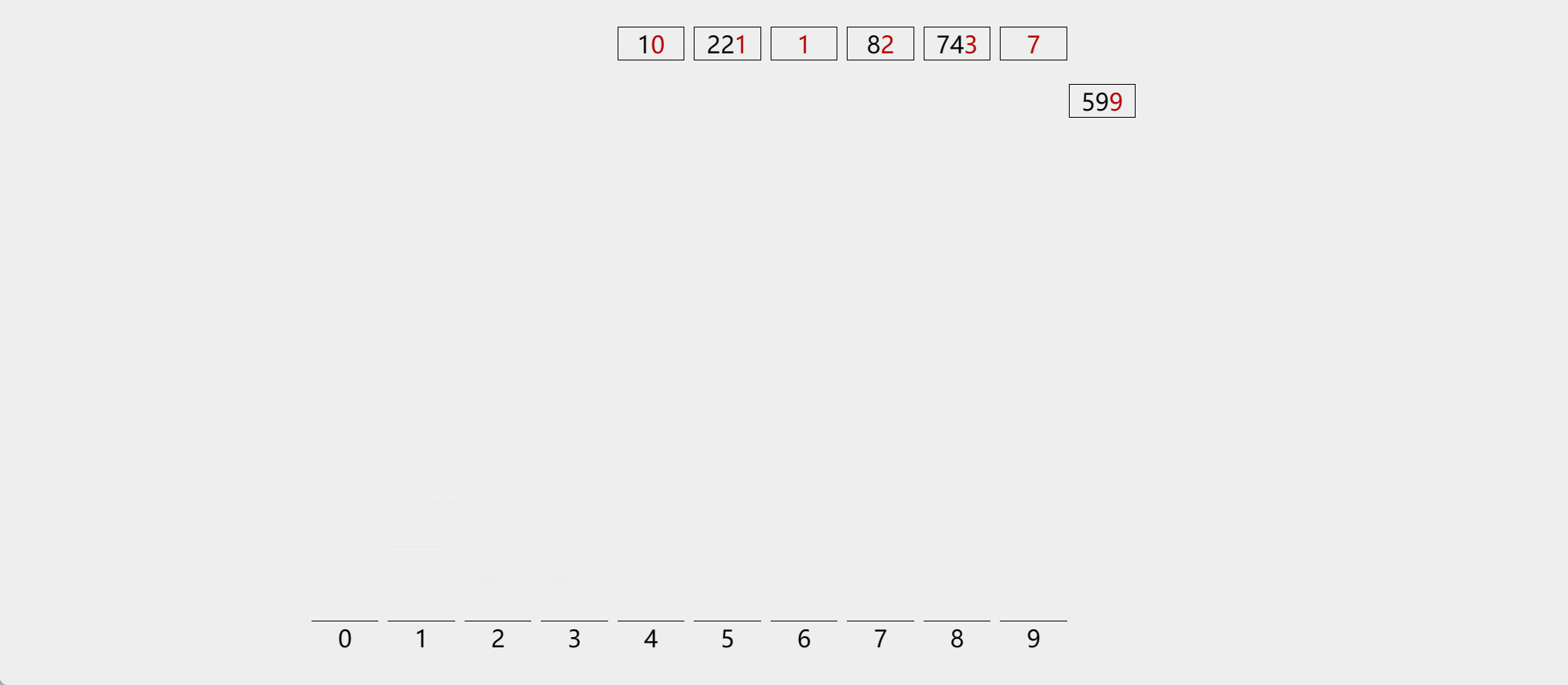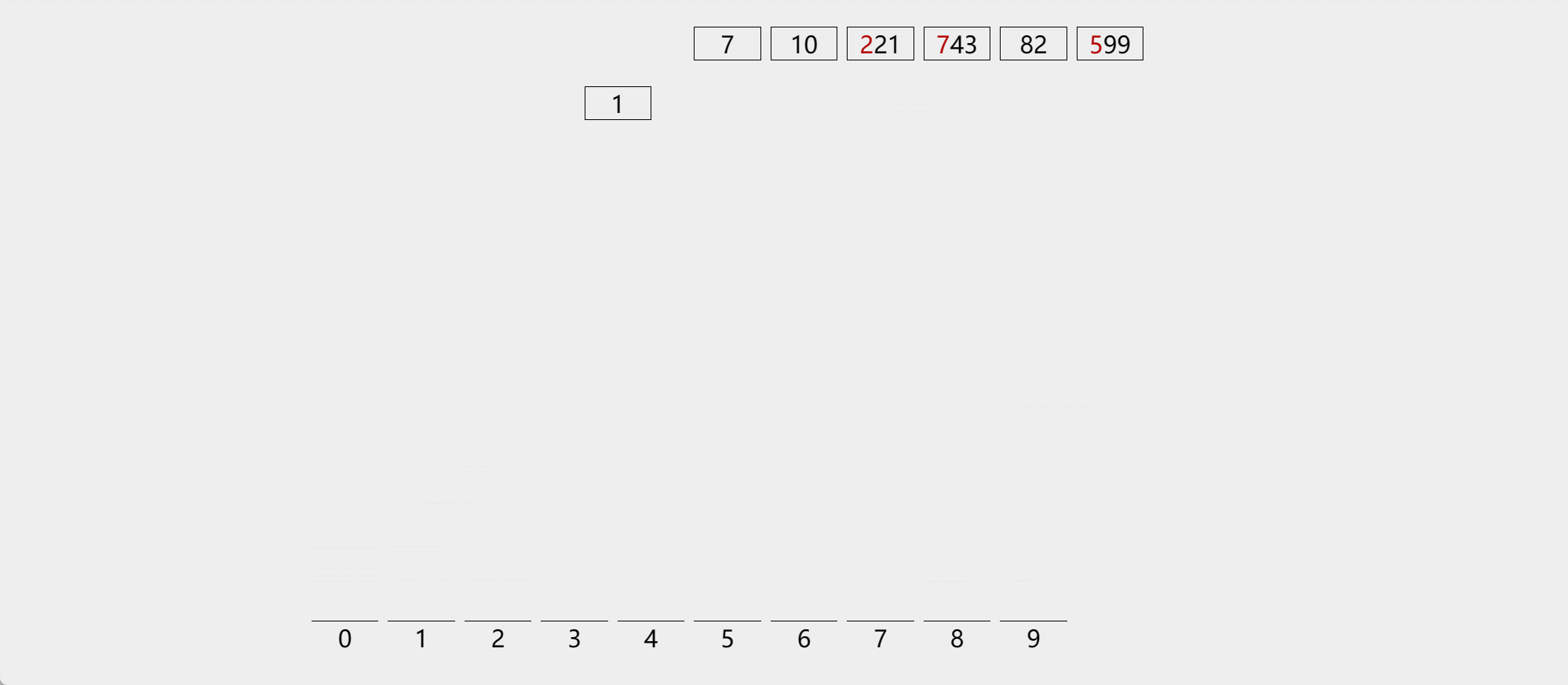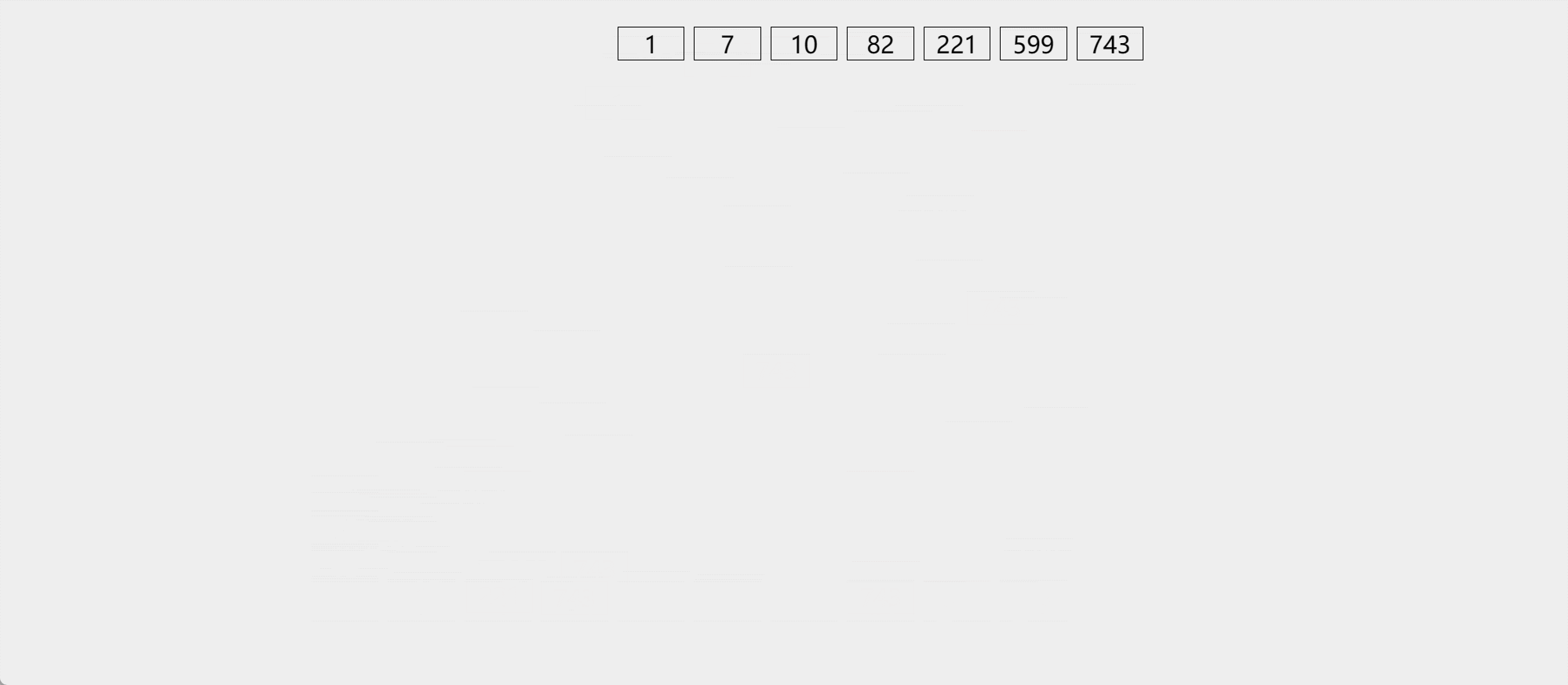


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通