09 查找 | 数据结构与算法

1. 查找

1. 查找的概念

查找：就是在数据集合中寻找满足某种条件的数据对象
查找表：是由同一类型的数据元素组成的数据集合
关键字：数据元素中某个数据项的值，用来标识一个数据元素
主关键字：可以唯一标识一个数据元素的关键字
次关键字：用以识别若干记录的关键字

2. 查找的基本形式

静态查找：在查找时只对数据元素进行查询或检索，查找表称为 静态查找表
动态查找：在实施查找的同时，插入查找表中不存在的记录，或从查找表中删除已存在的某个记录，查找表称为 动态查找表

3. 查找方法

顺序表和链表的查找：将给定的K值与查找表中记录的关键字逐个进行比较，找到要查找的记录
散列表的查找：根据给定的K值直接访问查找表，从而找到要查找的记录
索引查找表的查找：首先根据索引确定待查找记录所在的块，然后再从块中找到要查找的记录

4. 查找算法分析

在查找过程中关键字的平均比较次数或平均读写磁盘次数，这个标准也称为 平均查找长度 \(ASL(Average Search Length)\)，通常它是查找结构中对象总数n或文件结构中物理块总数 n 的函数
平均查找长度：设查找第 \(i\) 个元素的概率为 \(p_i\)，查找到第 \(i\) 个元素所需比较次数为 \(c_i\)
\[ASL_{success} = \sum_{i=1}^np_i\cdot c_i\space(\sum_{i=1}^np_i = 1) \]

2. 查找方法

1. 顺序查找

原理：数据以线性表的形式组织进行表示（称为查找表），其存储结构可以是连续设计方式或链接设计方式；从表中最后一个元素开始，顺序用各元素的关键字与给定值x进行比较，若找到与其值相等的元素，则查找成功，给出该元素在表中的位置；否则，若直到第一个记录仍未找到关键字与x相等的对象，则查找失败
\(ASL_{succ} = \sum_{i=1}^n\frac{1}{n}(n-i+1) = \frac{n+1}{2}\)
\(ASL_{fail} = n + 1\)
时间复杂度\(O(n)\)

算法

/*return the index of searching value, if fail return -1;*/
int seq_search(int arr[], int val, int len) {
    int ptr = len - 1;
    while (ptr >= 0 && arr[ptr] != val) --ptr;
    return ptr;
}

2. 二分查找

原理：前提条件是查找表中的所有记录是按关键字有序(升序或降序) 组成的线性表；查找过程中，先确定待查找记录在表中的范围，然后逐步缩小范围(每次将待查记录所在区间缩小一半)，直到找到或找不到记录为止
\(ASL = \sum_{i=1}^np_i\cdot c_i = \frac{1}{n}\sum_{j=1}^hj\cdot 2^{j-1}=\frac{n+1}{n}\log(n+1)-1\)，当\(n\)很大的时候，\(ASL\approx\log(n+1)-1\)（\(h\)为查找二叉树的最大高度）
时间复杂度\(O(\log n)\)

算法

/*return the index of searching value, if fail return -1;*/
int binary_search(int arr[], int val, int len) {
    int left = 0, right = len - 1;
    while(left <= right) {
        int mid = (left + right) / 2;
        if(arr[mid] == val) return mid;
        else if(arr[mid] > val) right = mid - 1;
        else left = mid + 1;
    }
    return -1;
}

3. 分块查找

原理：又叫索引顺序查找，将查找表分成几块。块间有序，即第i+1块的所有记录关键字均大于(或小于)第i块记录关键字；块内无序；在查找表的基础上附加一个索引表，索引表是按关键字有序的
\(ASL = L_b + L_w=\frac{b+1}{2}+\frac{s+1}{2}\)，其中表长为\(n\)，每块记录数为\(s\)，均分为\(b=\lceil n/s\rceil\)

4. \(Fibonacci\)查找

\(Fibonacci\)数列定义：F[0] = 0, F[1] = 1, F[i] = F[i - 1] + F[i - 2]
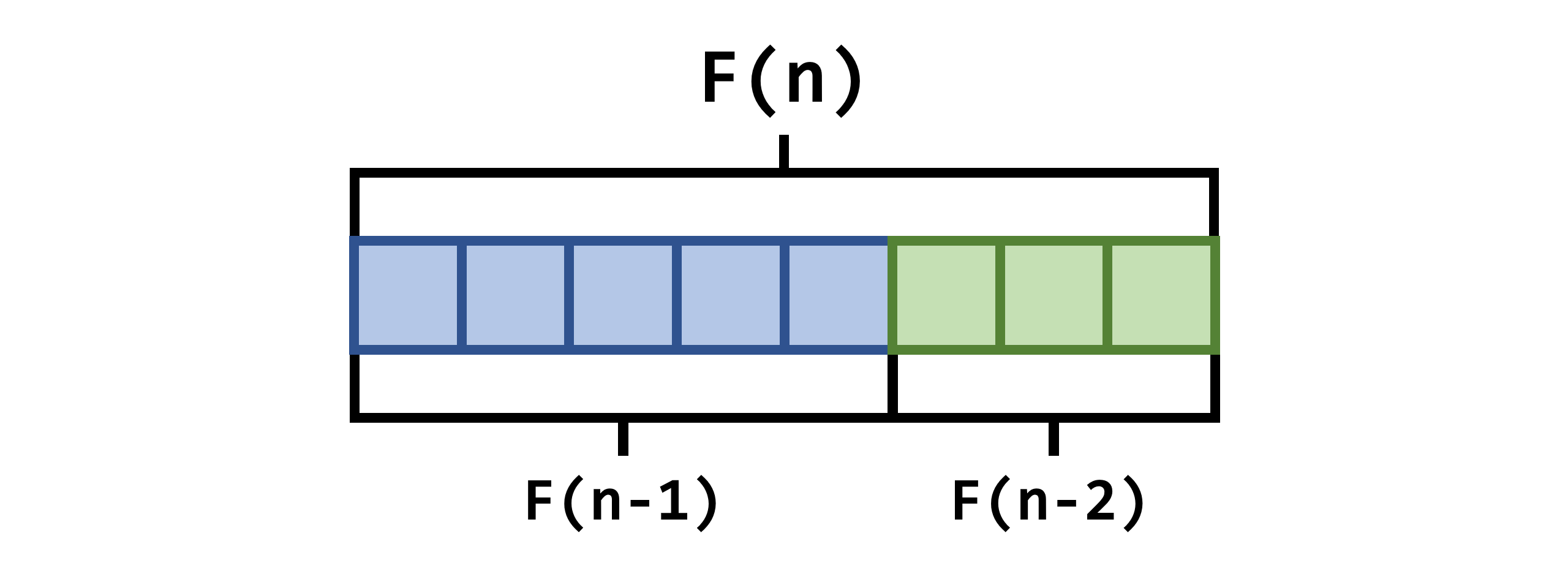
原理：设查找表中的记录数比某个\(Fibonacci\)数小1，即设n = F(j) - 1，用low, high, mid表示待查找区间的下界、上界和分割位置，初始值low = 1, high = n
1. 取分割位置mid = F(j - 1)
2. 比较给定的key与分割位置记录的关键字
  1. 相等：查找成功
  2. 小于：待查记录在区间的前半段(区间长度为F(j - 1) - 1)，修改下界high = mid - 1
  3. 大于：待查记录在区间的后半段(区间长度为F(j - 2) - 1)，修改下界low = mid + 1
算法分析：\(Fibonacci\)查找在最坏情况下性能比折半查找差，但是\(Fibonacci\)查找的优点是分割时只需进行加、减运算

算法

int Fibonacci(int num) {
   if (num <= 1) return num;
   else {
      int f0 = 0, f1 = 1, temp;
      for (int i = 2; i <= n; ++i) {
         temp = f0 + f1;
         f0 = f1;
         f1 = temp;
      }
      return temp;
   }
}
/*return the index of searching value, if fail return -1;*/
int Fibonacci_search(int arr[], int n, int key) { // arr [1~n]
   int low = 1, high = n, mid, k = 0;
   while (n > Fibonacci(k) - 1) ++k;
   for (int i = n; i < Fibonacci(k) - 1; ++i) {
      a[i] = a[n];   // fill elements at the end 
   }
   while (low <= high) {
      mid = low + Fibonacci(k - 1) - 1;
      if (key < a[mid]) {
         high = mid - 1;
         --k;
      }
      else if (key > a[mid]) {
         low = mid + 1;
         k -= 2;
      }
      else {
         if (mid <= n) return mid;
         else return n;
      }
   }
   return -1;
}

3. 散列（哈希表）

1. 散列

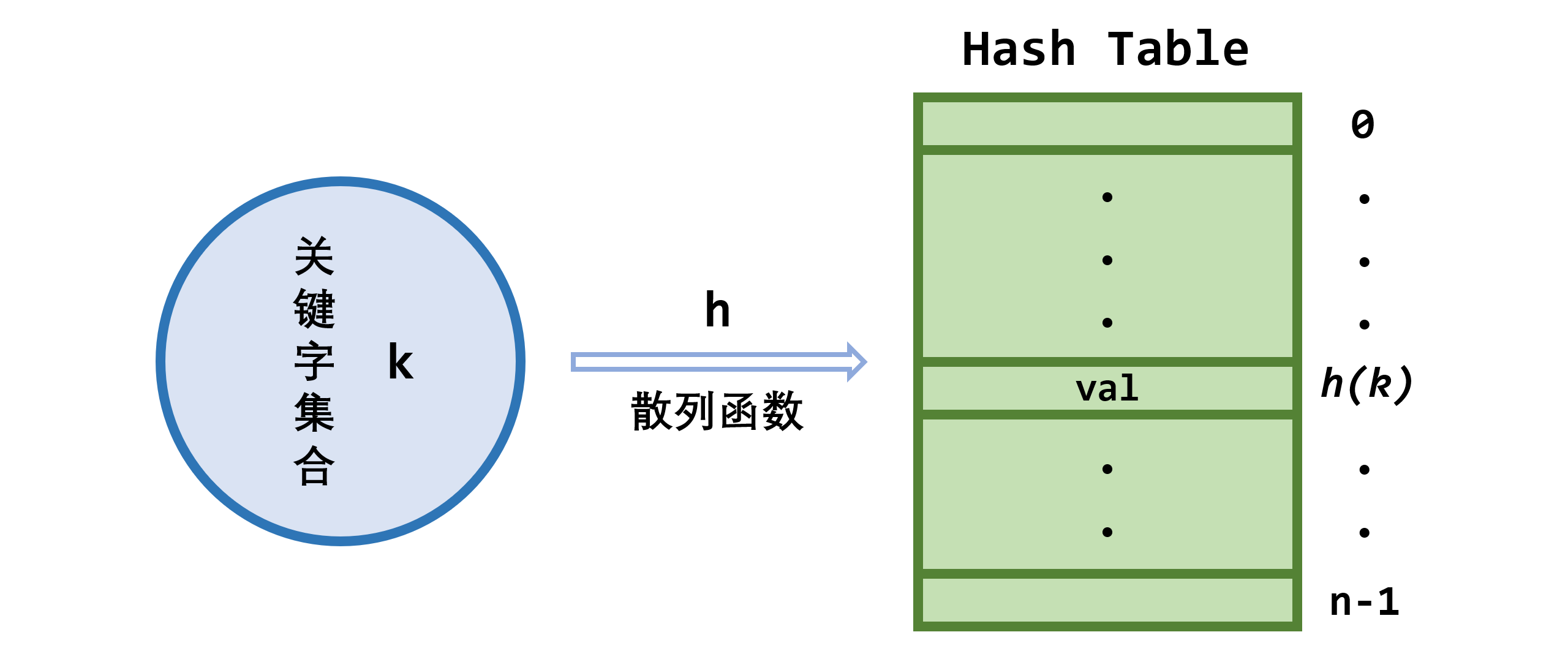
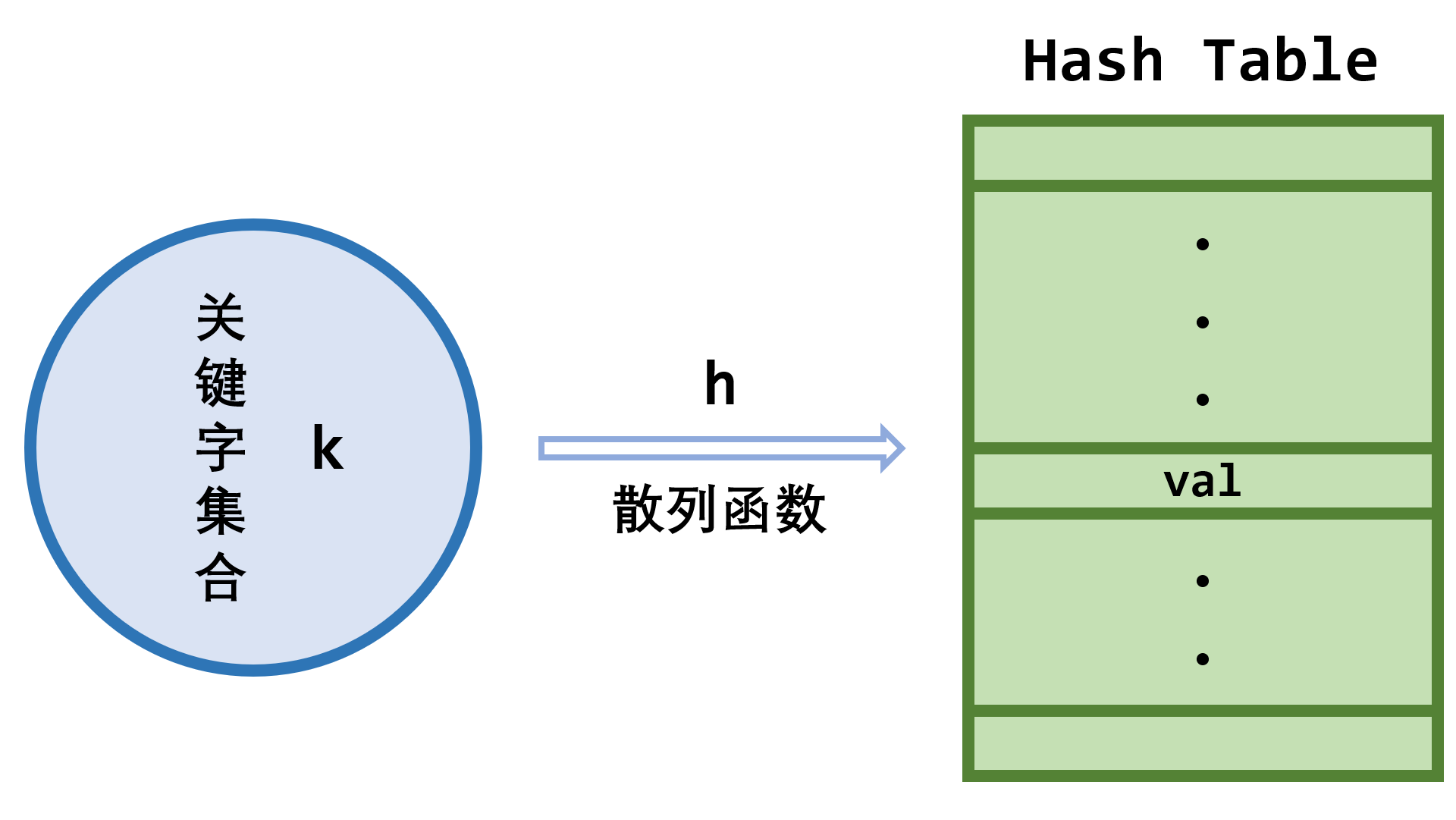
散列技术的基本思想：把记录元素的存储位置和该记录的关键字的值之间建立一种 映射关系，即散列函数，关键字的值在这种关系下的像，就是相应记录在表中的存储位置
期望时间复杂度\(O(1)\)
散列表（哈希（\(Hash\)）表）：存放记录的数组，数组的每个单元被称为桶(\(bucket\))
散列地址：对于任意关键字\(k\)，函数值\(h(k)\)称为\(k\)的 散列地址
冲突：不同的关键字具有相同的散列地址的现象叫做 散列冲突

2. 哈希函数的构造方法

哈希函数的构造原则
1. 计算简单：哈希函数不应该有很大的计算量，否则会降低查找效率
2. 分布均匀：尽量均匀分布在地址空间，保证存储空间的有效利用并减少冲突
哈希函数的构造方法分类
1. 直接定址法：此类函数直接取关键字或关键字的某个线性函数值作为散列地址，这类散列函数是一对一的映射，一般不会产生冲突
  1. 哈希函数：\(Hash(key) = a*key+b\)
  2. 要求：散列地址空间的大小与关键字集合的大小相同
  3. 适用情况：事先知道关键字的值，关键字取值集合不是很大且连续性较好
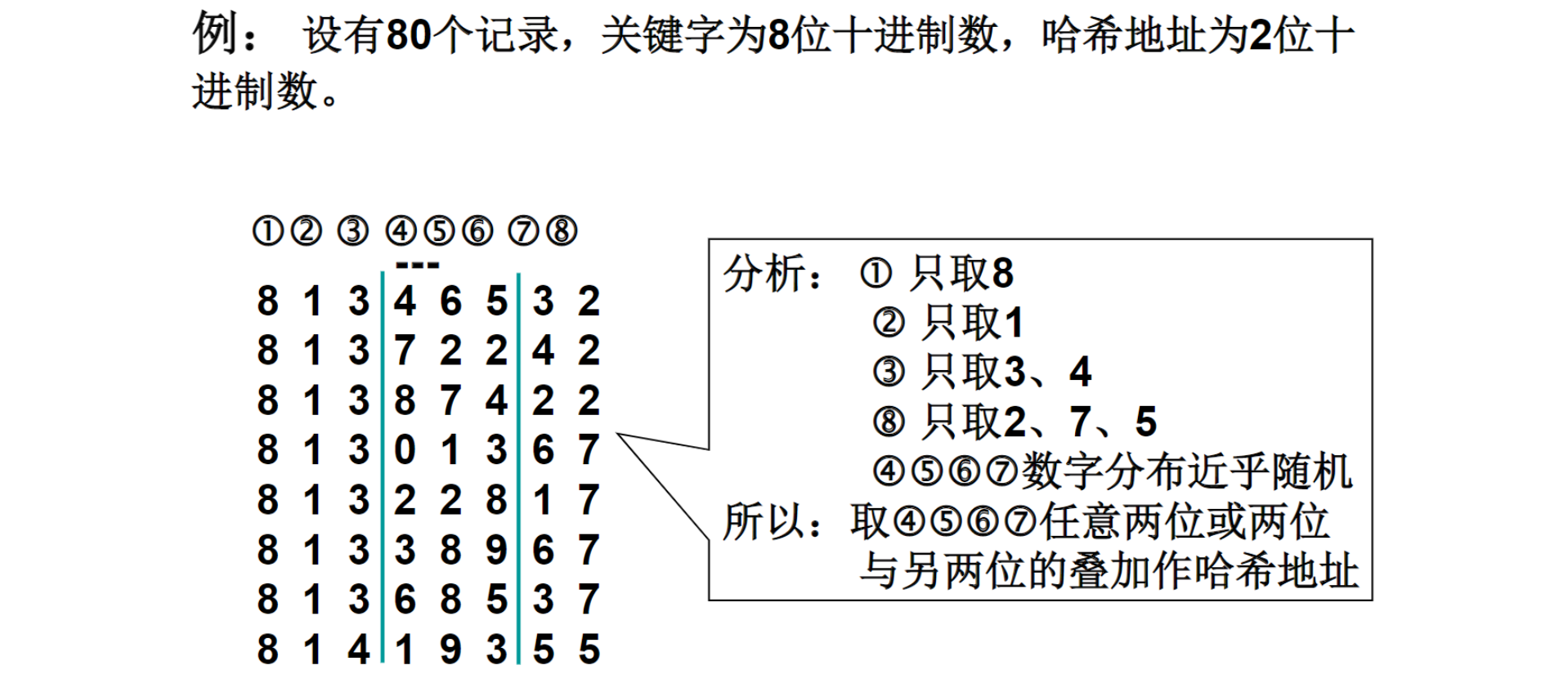
2. 数字分析法：设有\(n\)个\(d\)位数每一位可能有\(r\)种不同的符号。这 \(r\) 种不同的符号在各位上出现的频率不一定相同，可能在某些位上分布均匀些；在某些位上分布不均匀，只有某几种符号经常出现；可根据散列表的大小，选取其中各种符号分布均匀的若干位作为散列地址
  1. 哈希函数：对关键字进行分析，取关键字的若干位或组合作为哈希地址
  2. 适用情况：适用于关键字位数比哈希地址位数大，且可能出现的关键字事先知道的情况
3. 平方取中法：将关键字平方后取中间几位作为哈希地址
  - 适用情况：这种方法适于事先不知道关键字的分布情况且关键字的位数不是很大
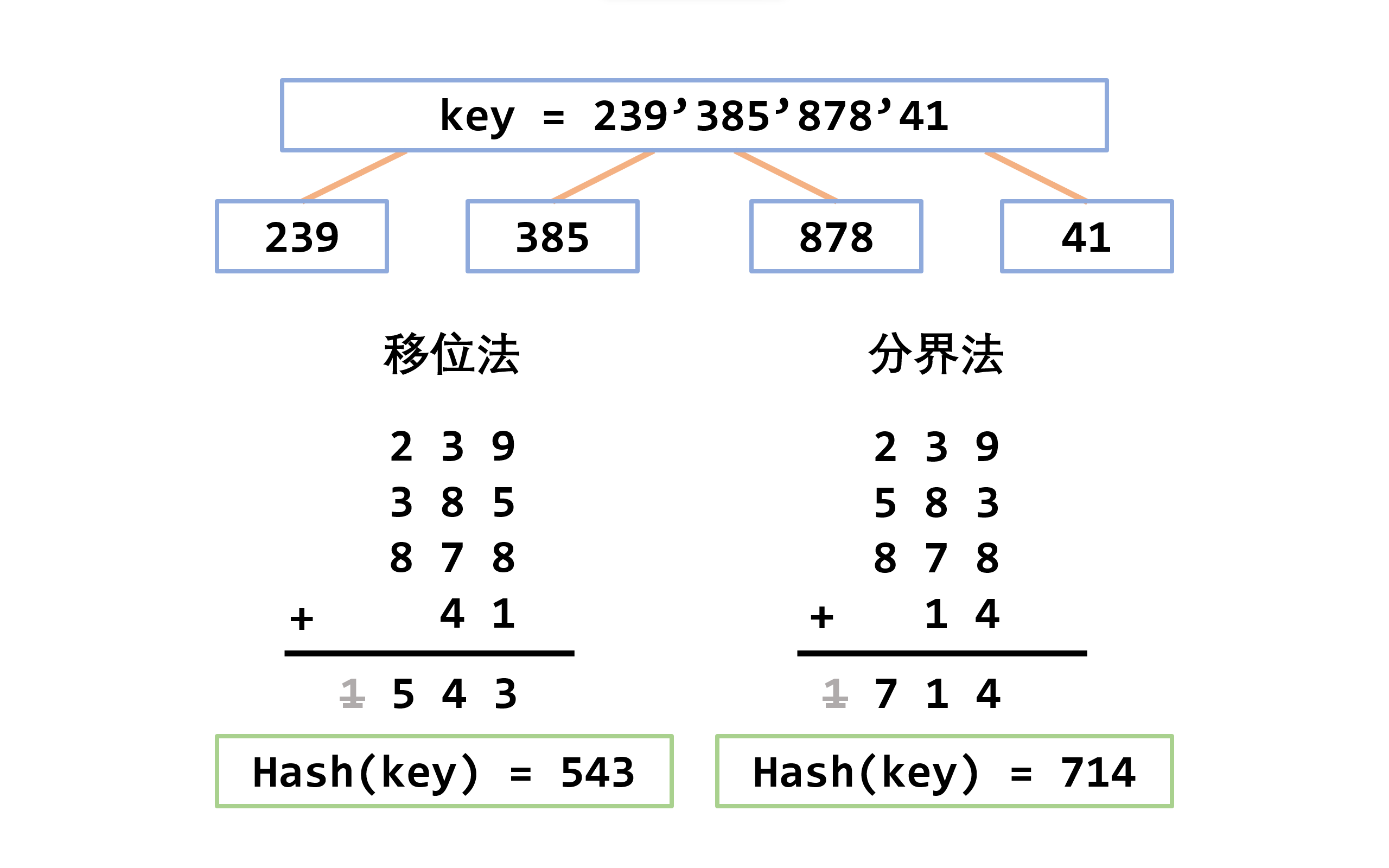
4. 折叠法：此方法把关键字自左到右分成位数相等的几部分，每一部分的位数应与散列表地址位数相同，只有最后一部分的位数可以短一些；把这些部分的数据叠加起来，就可以得到具有该关键字的记录的散列地址。有两种叠加方法：
  1. 移位法：把各部分的最后一位对齐相加
  2. 分界法：各部分不折断，沿各部分的分界来回折叠，然后对齐相加，将相加的结果当做散列地址
  - 适用情况：关键码位数很多，事先不知道关键码的分布
5. 除留余数法：设散列表中允许的地址数为\(m\),取一个不大于\(m\)，但最接近于或等于\(m\)的质数\(p\)，或选取一个不小于\(20\)的质因数的合数作为除数，利用哈希函数把关键字转换成散列地址
  1. 哈希函数：\(Hash(key) = key \% p\)
6. 随机数法：取关键字的随机函数值作哈希地址，即hash(key) = random(key)
  - 适用情况：当散列表中关键字长度不等时，该方法比较合适

3. 解决散列冲突的方法

开放定址法
1. 基本方法：当冲突发生时，形成某个探测序列；按此序列逐个探测散列表中的其他地址，直到找到给定的关键字或一个空地址(开放的地址)为止，将发生冲突的记录放到该地址中。散列地址的计算公式是 \(H_i(key) = (H(key) + d_i) \% m\)，其中\(m\)是散列表长度，\(d_i\)是第\(i\)次探测时的增量序列，\(H_i(key)\)是经第\(i\)次探测后得到的散列地址
2. 分类
  1. 线性探测法：将哈希表\(T[0:m]\)看作循环向量，当发生冲突时，从初次发生冲突的位置依次向后探测其他的地址
    1. 增量序列为：\(d_i=1, 2, 3, \cdots, m-1\)
    2. 探测方法：设初次发生冲突的地址是h，则依次探测T[h + 1], T[h+2]...，直到T[m - 1]时又循环到表头，再次探测T[0], T[1]...，直到T[h - 1]；探测过程终止的情况是
      1. 探测到的地址为空：表中没有记录。若是查找则失败；若是插入则将记录写入到该地址
      2. 探测到的地址有给定的关键字：若是查找则成功；若是插入则失败
      3. 直到T[h]：仍未探测到空地址或给定的关键字，散列表满
    3. 优点：只要散列表未满，总能找到一个不冲突的散列地址
    4. 缺点：每个产生冲突的记录被散列到离冲突最近的空地址上，从而又增加了更多的冲突机会(这种现象称为冲突的聚集)
  2. 二次探测法
    1. 增量序列为：\(d_i=1^2, -1^2, 2^2, -2^2\cdots, \pm k^2(k \le\lfloor\sqrt{m}\rfloor)\)
    2. 优点：探测序列跳跃式地散列到整个表中，不易产生冲突的聚集现象
    3. 缺点：不能保证探测到散列表的所有地址
  3. 伪随机探测法
    1. 增量序列为：伪随机函数来产生一个落在闭区间[1, m-1]的随机序列
再哈希法
1. 基本方法：构造若干个哈希函数，当发生冲突时，利用不同的哈希函数再计算下一个新哈希地址，直到不发生冲突为止
2. 优点：不易产生冲突的聚集现象
3. 缺点：计算时间增加
链地址法
1. 基本方法：将所有关键字散列地址相同的记录存储在一个单链表中，并用一维数组存放链表的头指针
2. 优点：不易产生冲突的聚集；删除记录也很简单
3. 例：已知一组关键字(19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10) ，哈希函数为：H(key) = key % 13，用链地址法处理冲突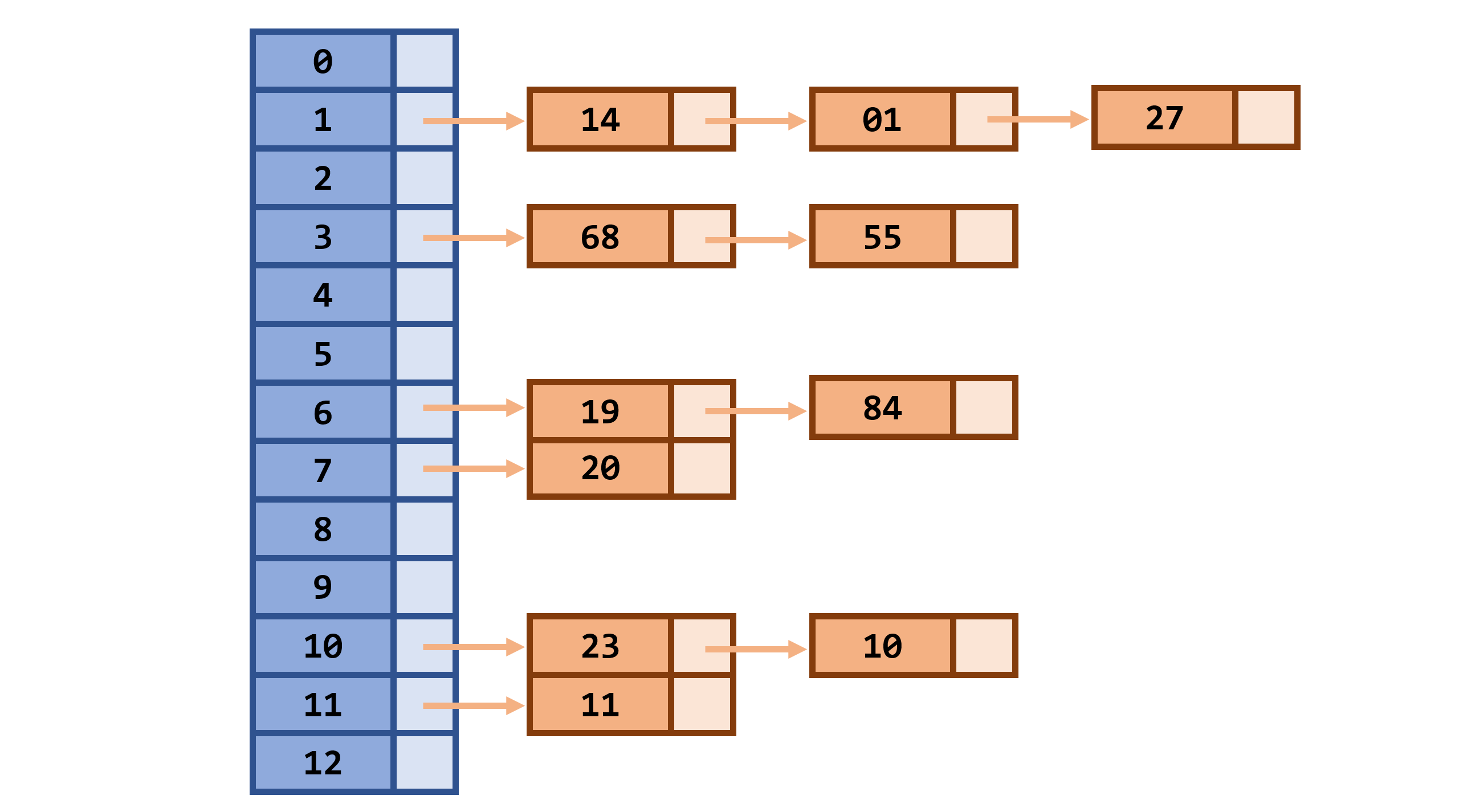
建立公共溢出区
1. 基本方法：在基本散列表之外，另外设立一个溢出表保存与基本表中记录冲突的所有记录。设散列表长为m，设立基本散列表hashtable[m]，每个分量保存一个记录；溢出表overtable[m]，一旦某个记录的散列地址发生冲突，都填入溢出表中
2. 例子：已知一组关键字(15, 4, 18, 7, 37, 47) ，散列表长度为7 ，哈希函数为：H(key) = key % 7，用建立公共溢出区法处理冲突
  
  HashTable 0 1 2 3 4 5 6
  
  关键字 7 15 37 \(\space\) 4 47 \(\space\)
  
  OverTable 0 1 2 3 4 5 6
  
  关键字 18 \(\space\)

HashTable	0	1	2	3	4	5	6
关键字	7	15	37	\(\space\)	4	47	\(\space\)

4. 哈希查找过程及分析

查找算法

开放定址法（线性探测）解决冲突

#define nullkey -1   // set -1 as nullkey

typedef struct {
   int key;
   int other_information;
} RecType;

int hash_search(RecType HashTable[], int key, int m) {
   int address, cnt = 0;
   address = hash(key);    // hash: hash function
   while (cnt < m && HashTable[address].key != nullkey) {
      if (HashTable[address].key == key) return address;
      else {
         address = (address + 1) % m;
         ++cnt;
      }
   }
   return -1;
}

链地址法解决冲突

typedef struct node {
   int key;
   node* link;
} HNode;

HNode* hash_search(HNode *HashTable[], int key) {
   int address = hash(key);   // hash: hash function
   if (HashTable[address] == nullptr) return nullptr;
   else {
      HNode *ptr = HashTable[address];
      while (ptr != nullptr) {
         if (ptr->key == key) return ptr;
         else ptr = ptr -> link;
      }
   }
   return nullptr;
}

哈希查找分析
1. 从哈希查找过程可见：尽管散列表在关键字与记录的存储地址之间建立了直接映象，但由于冲突，查找过程仍是一个给定值与关键字进行比较的过程，评价哈希查找效率仍要用\(ASL\)
2. 哈希查找时关键字与给定值比较的次数取决于
  1. 哈希函数
  2. 处理冲突的方法
  3. 填满因子 \(\alpha = \frac{表中填入的记录数}{哈希表长度}\)
3. 各种散列函数所构造的散列表的\(ASL\)（注意失败的长度计算取决于所给关键字可能的哈希地址取值范围而不是哈希表本身长度）
  1. 线性探测法
    1. \(ASL_{succ} \approx \frac{1}{2}(1+\frac{1}{1-\alpha})\)
    2. \(ASL_{fail} \approx \frac{1}{2}(1+\frac{1}{(1-\alpha)^2})\)
  2. 二次探测、伪随机探测、再哈希法
    1. \(ASL_{succ} \approx -\frac{1}{\alpha}\ln(1 - \alpha)\)
    2. \(ASL_{fail} \approx \frac{1}{1 - \alpha}\)
  3. 链地址法
    1. \(ASL_{succ} \approx 1 + \frac{\alpha}{2}\)
    2. \(ASL_{fail} \approx \alpha + e^{-\alpha}\)

posted @ 2023-01-27 22:39 RadiumStar 阅读(40) 评论(0) 编辑收藏举报

刷新页面返回顶部

GALAXY OF RADIUM

09 查找 | 数据结构与算法

1. 查找

1. 查找的概念

2. 查找的基本形式

3. 查找方法

4. 查找算法分析

2. 查找方法

1. 顺序查找

2. 二分查找

3. 分块查找

4. \(Fibonacci\)查找

3. 散列（哈希表）

1. 散列

2. 哈希函数的构造方法

3. 解决散列冲突的方法

4. 哈希查找过程及分析

公告