08 图 | 数据结构与算法
1. 图的基本概念
1. 图的定义
-
图:图 是由顶点的有穷非空集合和顶点之间边的集合组成的一种数据结构,通常表示为:
-
图的分类
- 无向图
- 无向边:如果顶点
- 无向图:如果图的任意两个顶点之间的边都是无向边,那么该图被称为 无向图
- 无向边:如果顶点
- 有向图
- 有向边:如果顶点
- 有向图:如果图的任意两个顶点之间的边都是有向边,那么该图被称为 有向图
- 有向边:如果顶点
- 无向图
-
完全图
- 无向图:在具有
- 有向图:在具有
- 无向图:在具有
-
顶点的度
- 无向图的度:一个顶点
- 有向图的度
- 出度:以顶点
- 入度:以顶点
- 出度:以顶点
- 无向图的度:一个顶点
-
路径
- 无向图的路径:在无向图
- 有向图的路径:在有向图
- 路径的 长度:路径上边的数量
- 带权图的路径长度:路径上各边的权值之和
- 简单路径:如果路径上的各顶点
- 无向图的路径:在无向图
-
子图:如果图
-
连通图和连通分量(无向图)
- 连通性:顶点的连通性:在无向图中,若从顶点
- 连通图:如果一个无向图中任意一对顶点都是连通的, 则称此图是 连通图
- 连通分量:非连通图的极大连通子图叫做 连通分量
- 连通性:顶点的连通性:在无向图中,若从顶点
-
强连通图与强连通分量
- 顶点的强连通性:在有向图中, 若对于每一对顶点
- 强连通图:如果一个有向图中任意一对顶点都是强连通的, 则称此有向图是 强连通图
- 强连通分量:非强连通图的极大强连通子图叫做 强连通分量
- 顶点的强连通性:在有向图中, 若对于每一对顶点
-
生成树:假设一个连通图有
2. 图与其他数据结构的比较
- 比较一
1. 在线性结构中,数据元素之间仅具有线性关系(1:1)
2. 在树结构中,结点之间具有层次关系(1:n)
3. 在图结构中,任意两个点之间都可能有关系(m:n) - 比较二
1. 在线性结构中,数据元素之间的关系为 前驱和 后继
2. 在树结构中,结点之间的关系为 双亲和孩子
3. 在图结构中,顶点之间的关系为 邻接
3. 图的存储
-
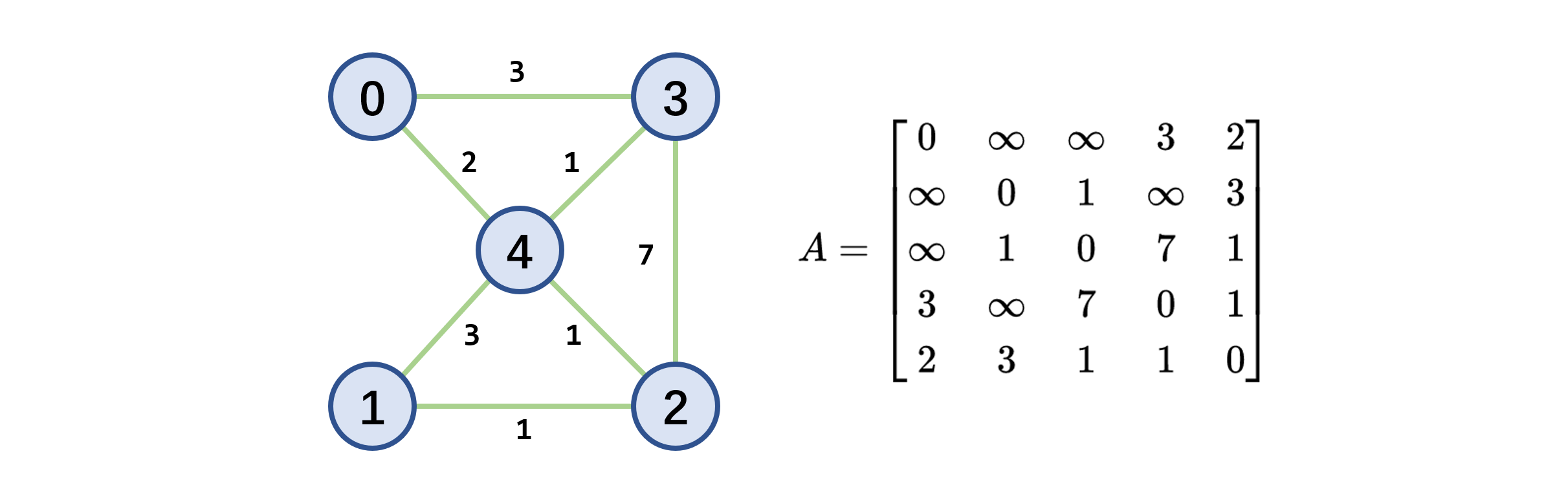
邻接矩阵表示法
-
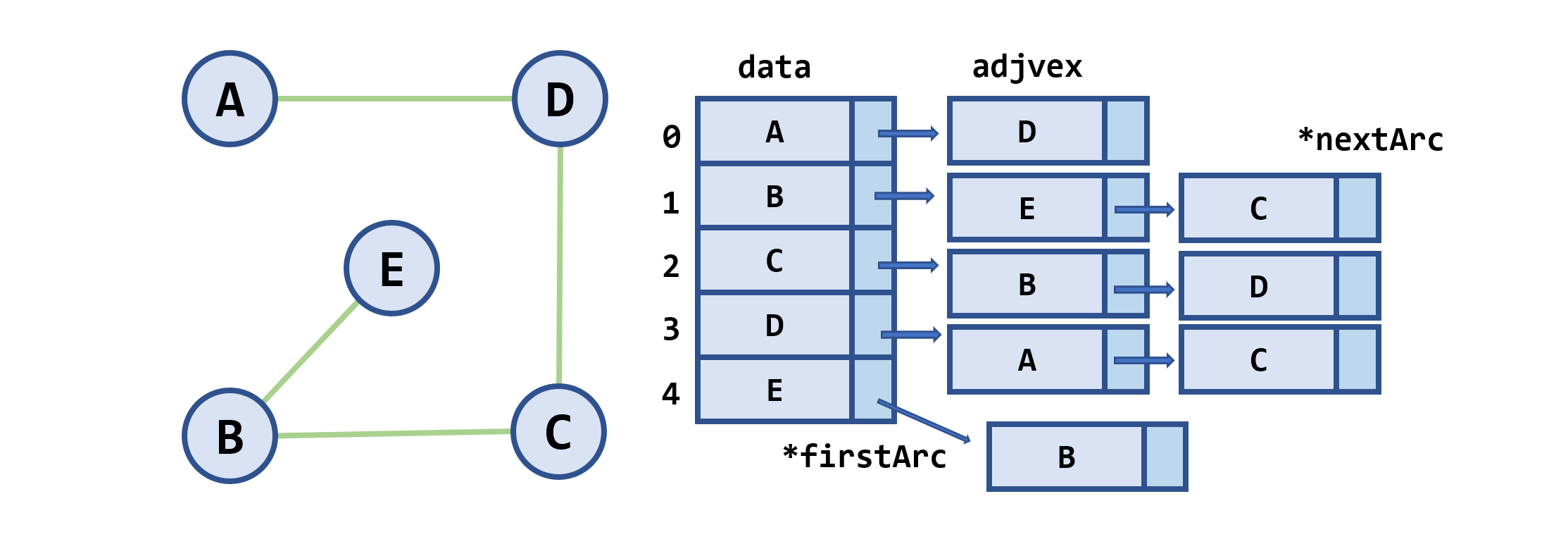
邻接表
-
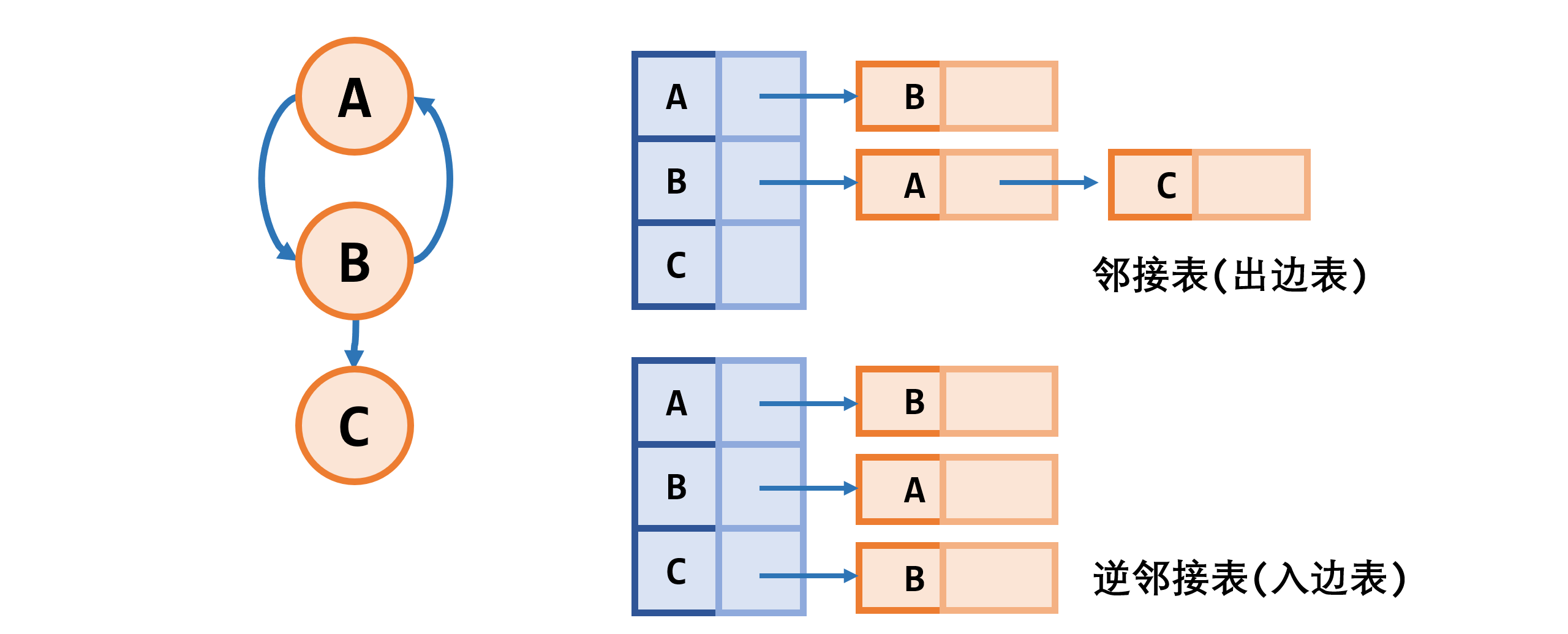
有向图的十字链表
-
无向图的邻接多重表
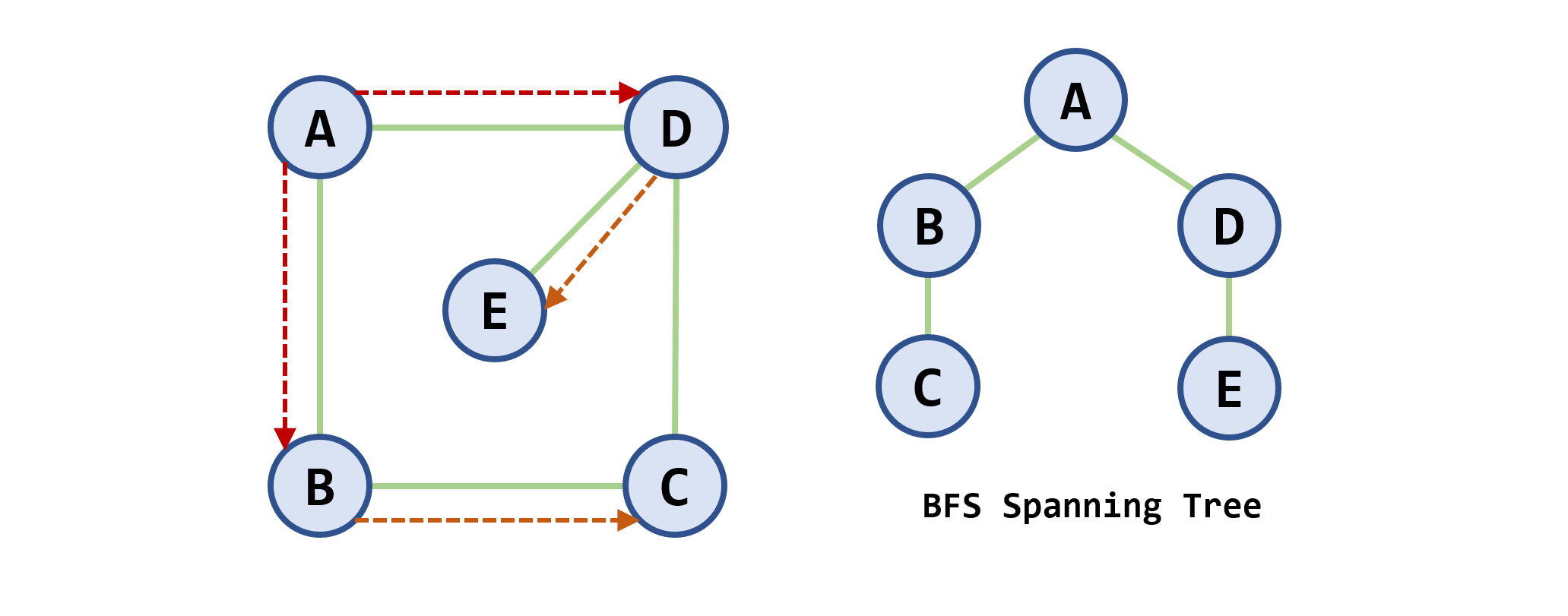
2. 图的遍历
1. 图的遍历
- 定义:从图中某一顶点出发访遍图中其余顶点,且使每个顶点仅被访问一次,就叫做图的遍历
- 分类:深度优先搜索
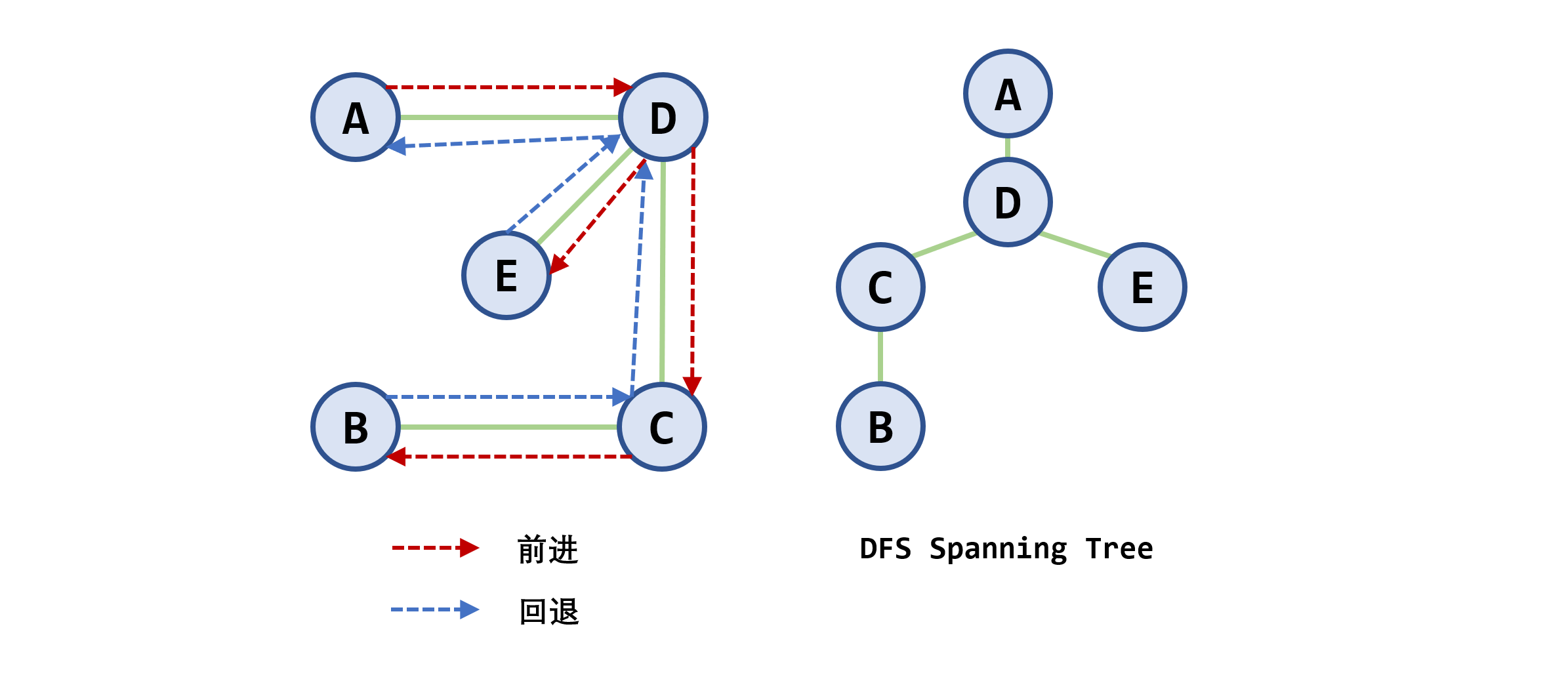
2. 深度优先搜索
-
定义:在访问图中某一起始顶点
-
算法:运用栈(递归)结构存储待
-
时间复杂度
- 邻接表:扫描边的时间为
- 邻接矩阵:查找每一个顶点的所有的边,所需时间为
- 邻接表:扫描边的时间为
3. 广度优先搜索
-
定义:在访问了起始顶点
-
算法:运用队列结构存储待
-
时间复杂度
- 邻接表:遍历图的时间复杂性为
- 邻接矩阵:遍历图中所有的顶点所需的时间为
- 邻接表:遍历图的时间复杂性为
3. 并查集
1. 并查集的定义
- 并查集:对于一个集合
- 并查集的基本结构:用树表示集合,不同的树是不同的集合,并查集中包含了多棵树,表示并查集中不同的子集,树的集合是森林,所以并查集属于森林
2. 并查集的基本操作
- 初始化
find:返回node所属集合树的根节点join:合并两个点所属的集合
3. 并查集的优化
- 优化原因:上面的实现,每一次
find时间复杂度为 - 优化方法
- 方法一:按秩合并:记录这棵树的高度(记为
- 方法二:路径压缩:查询时我们需沿着元素所在的树从下往上查询,最终找到这棵树的根,表明这个元素与其根对应元素属于同一组。因为在此查询过程中我们会经过许多节点,而如果我们能将这个元素直接指向根节点,那么就能节省许多查询的时间。同时,在查询过程中,每次经过的节点,我们都可以同时将他们一起直接指向根节点。这样做的话,我们再查询这些节点时,就能很快找到根
- 方法一:按秩合并:记录这棵树的高度(记为
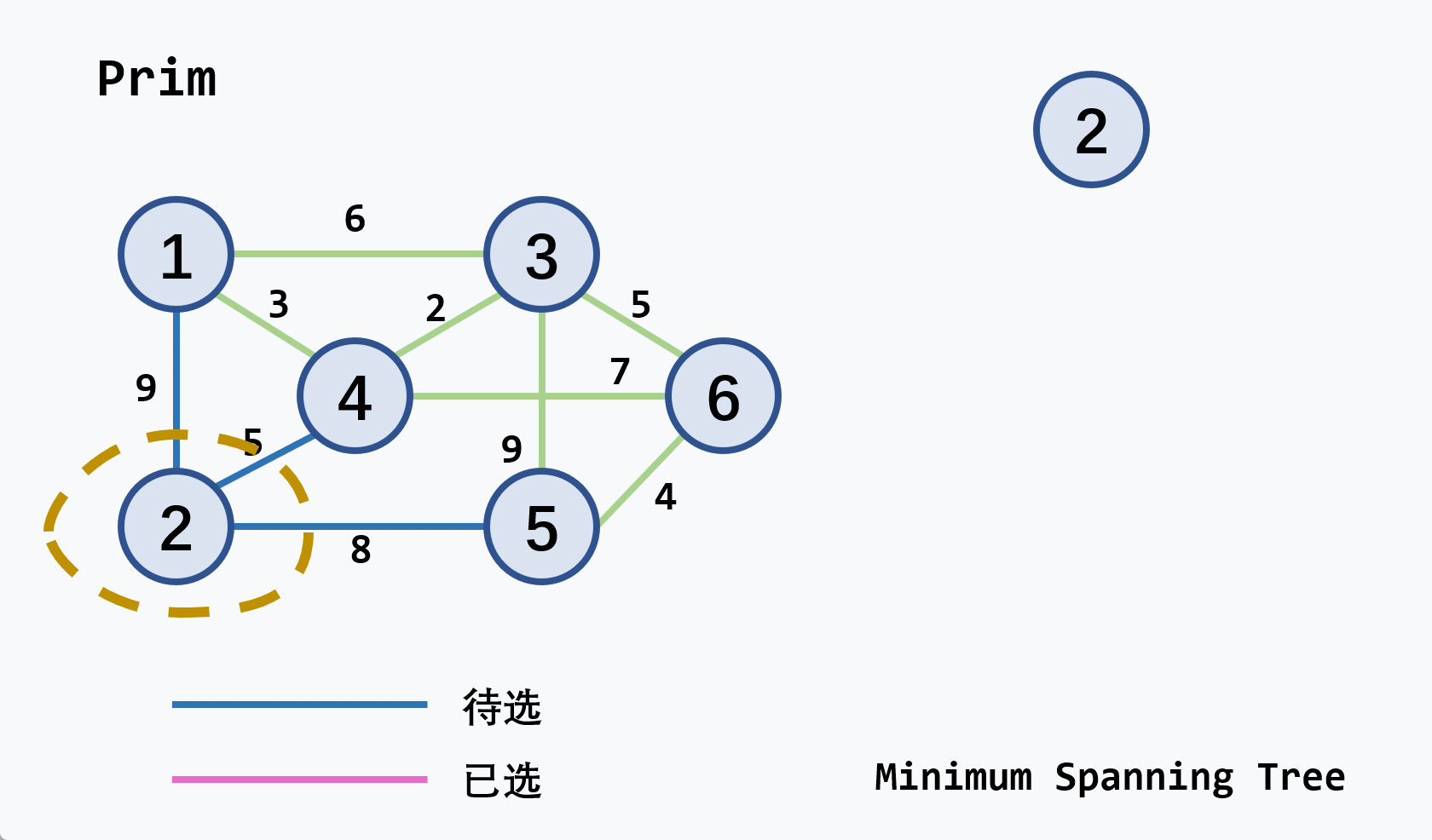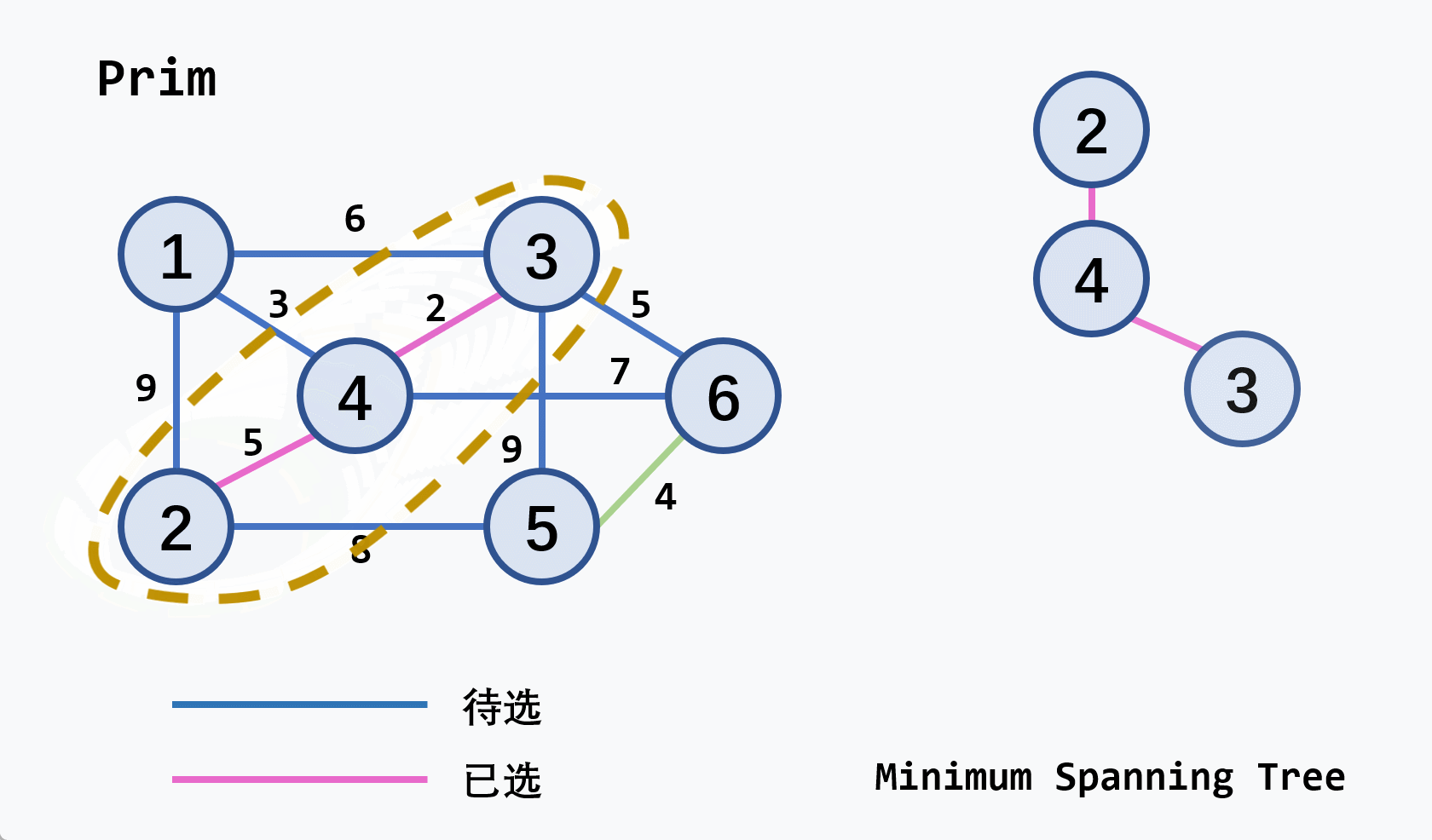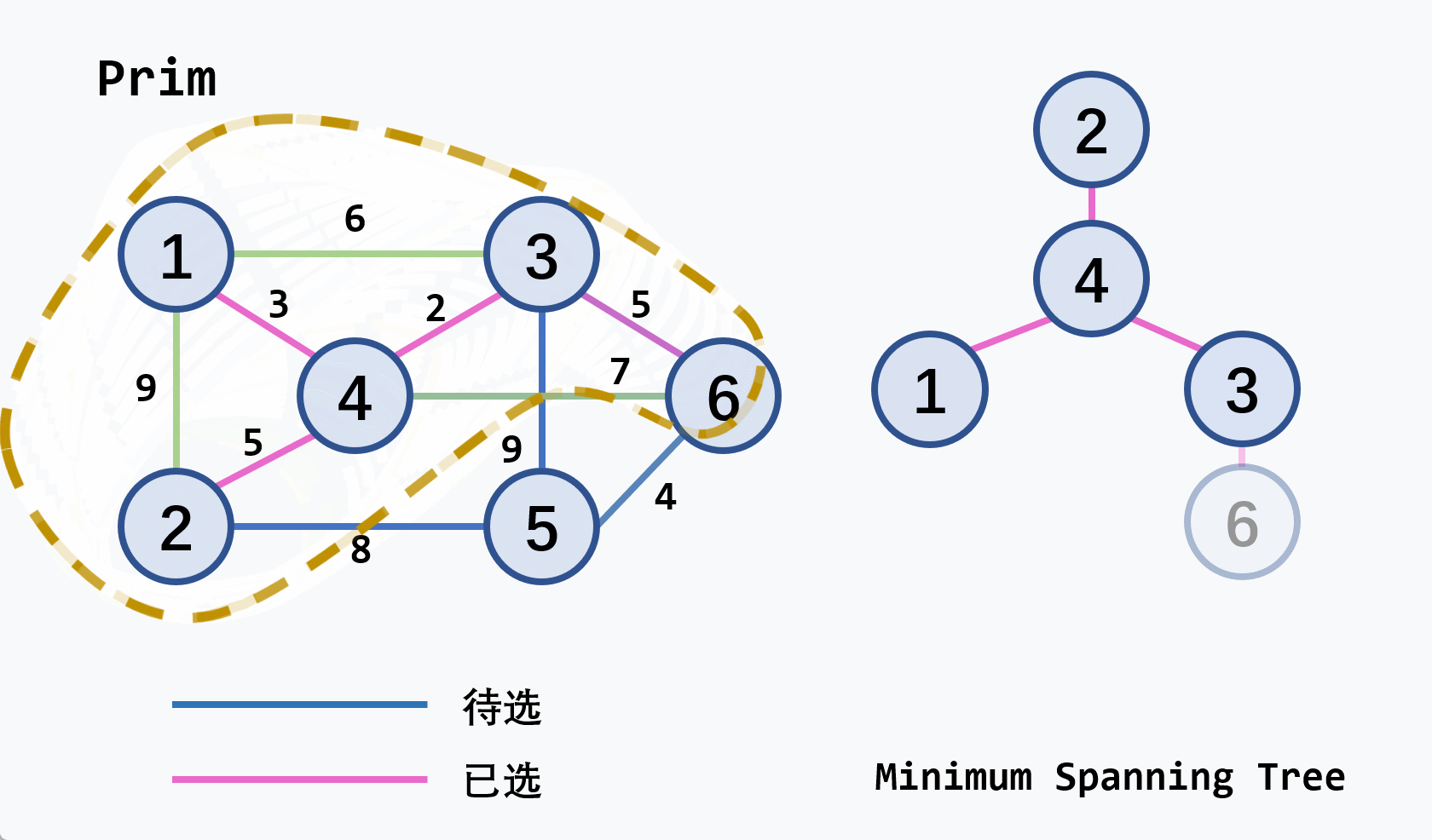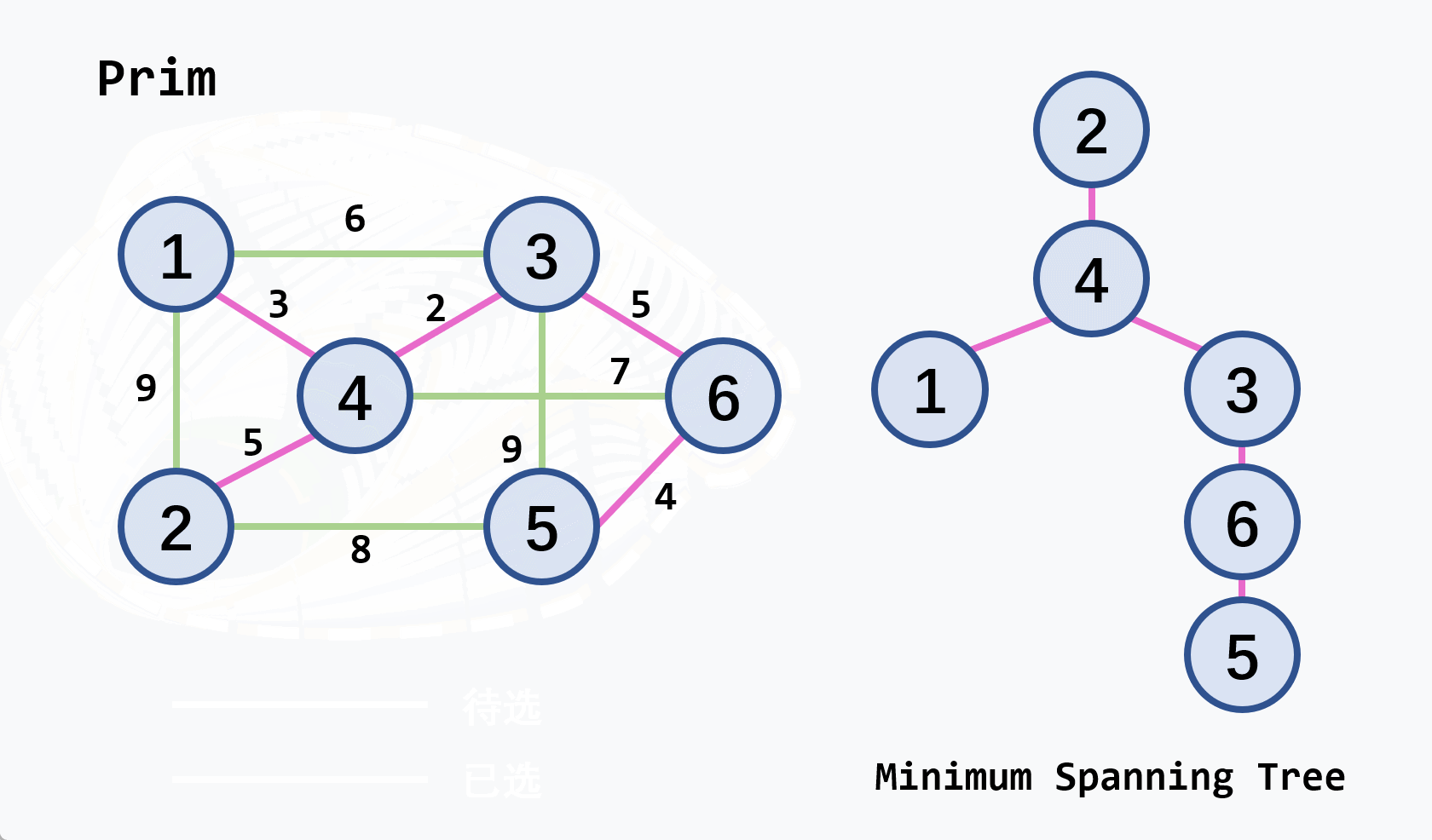
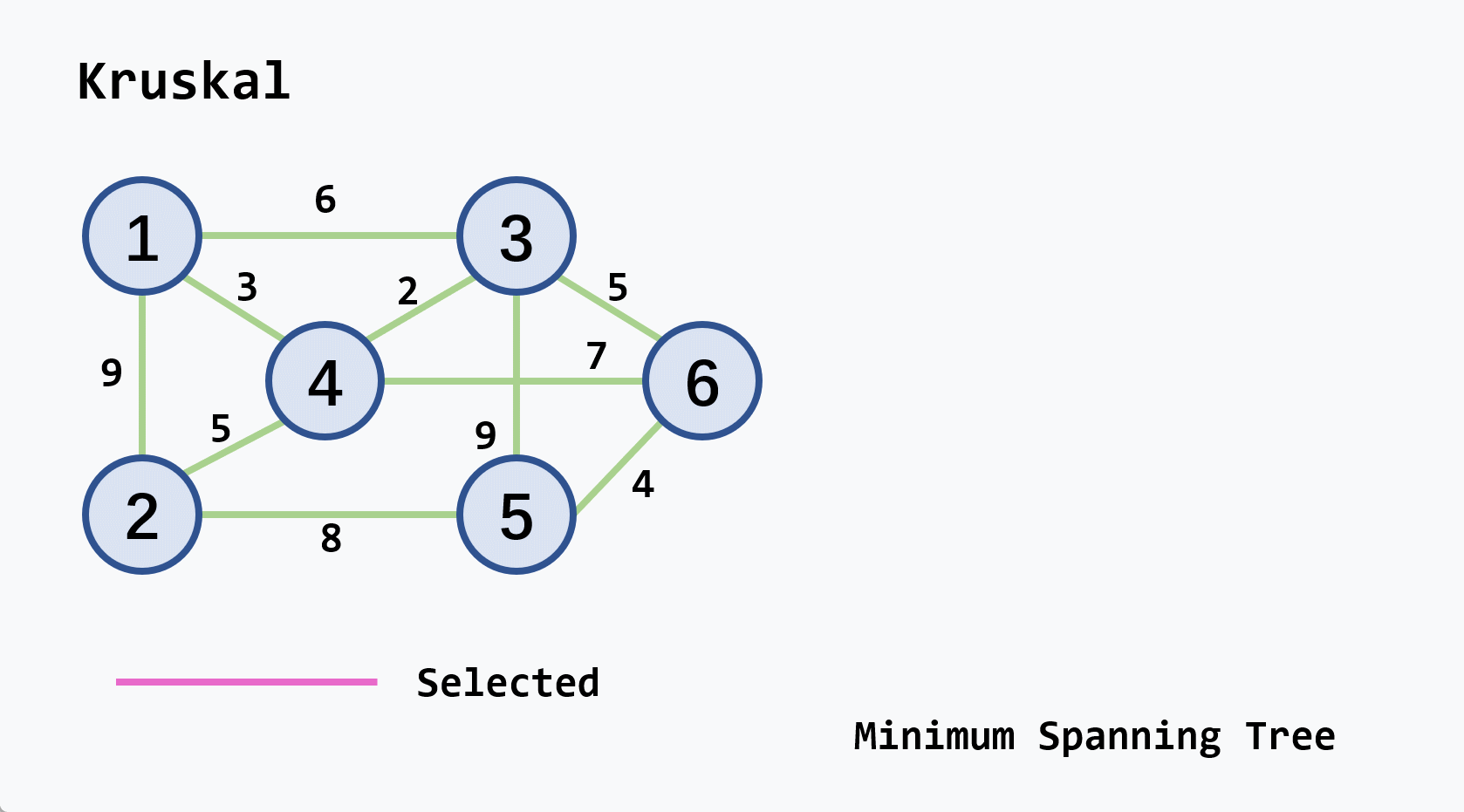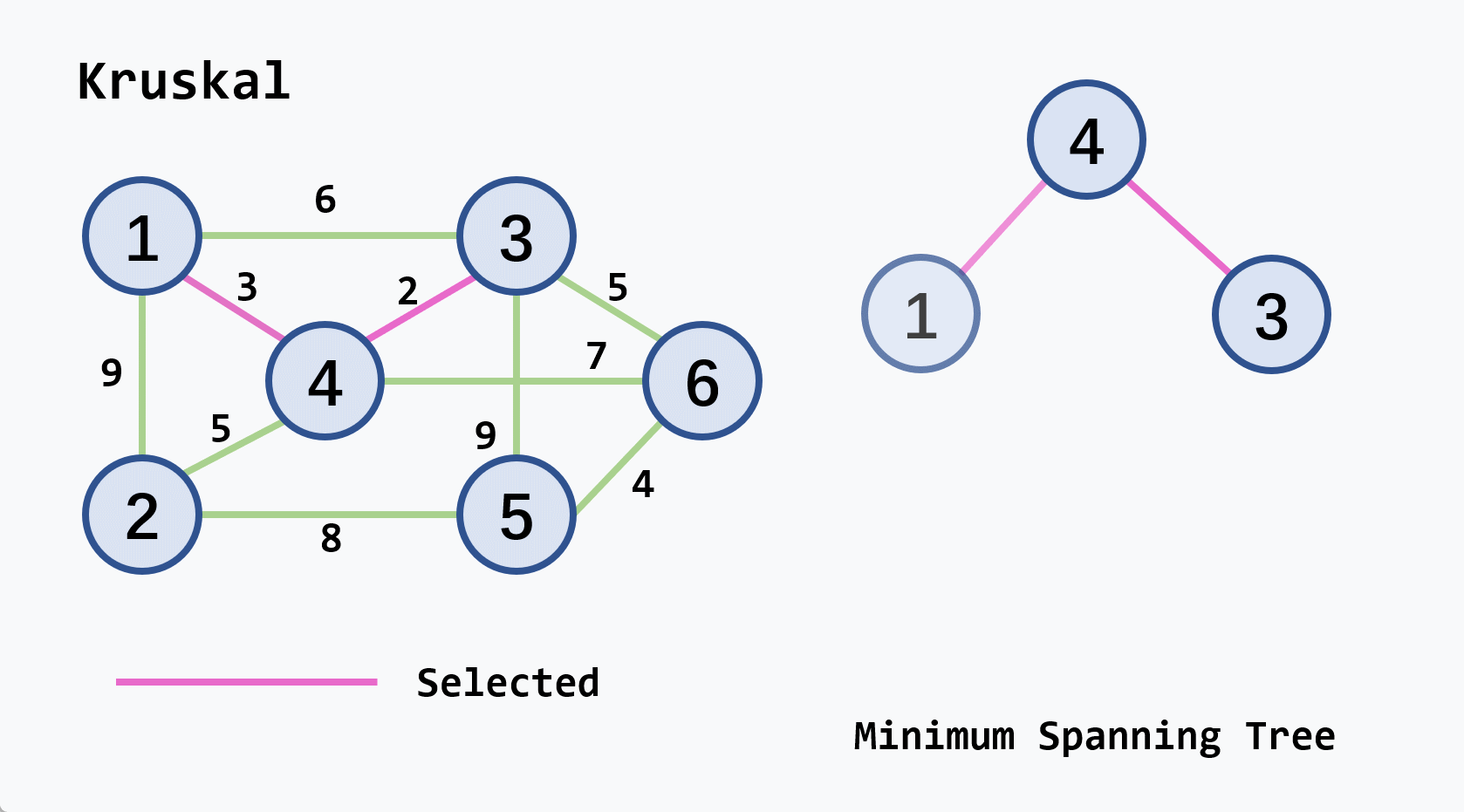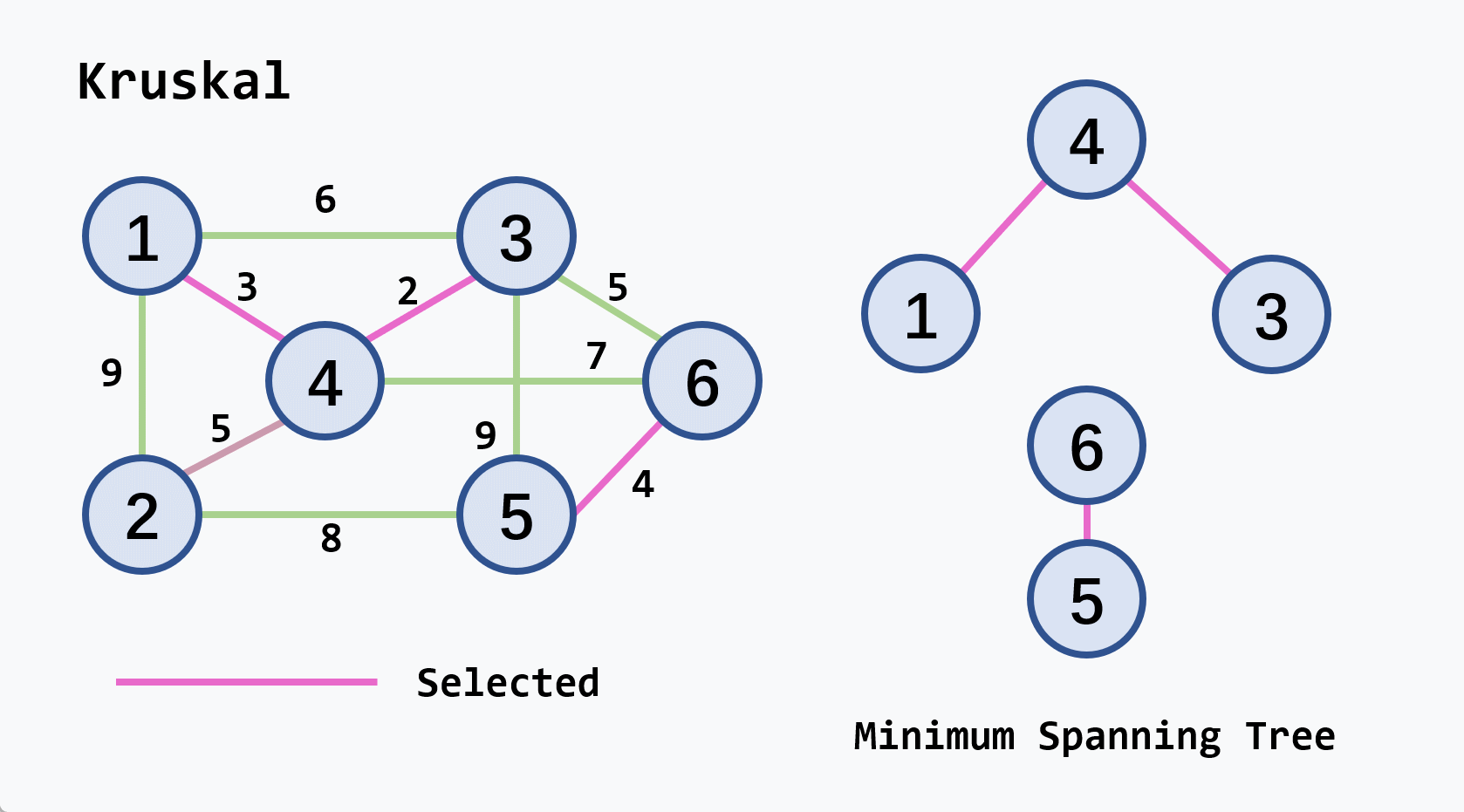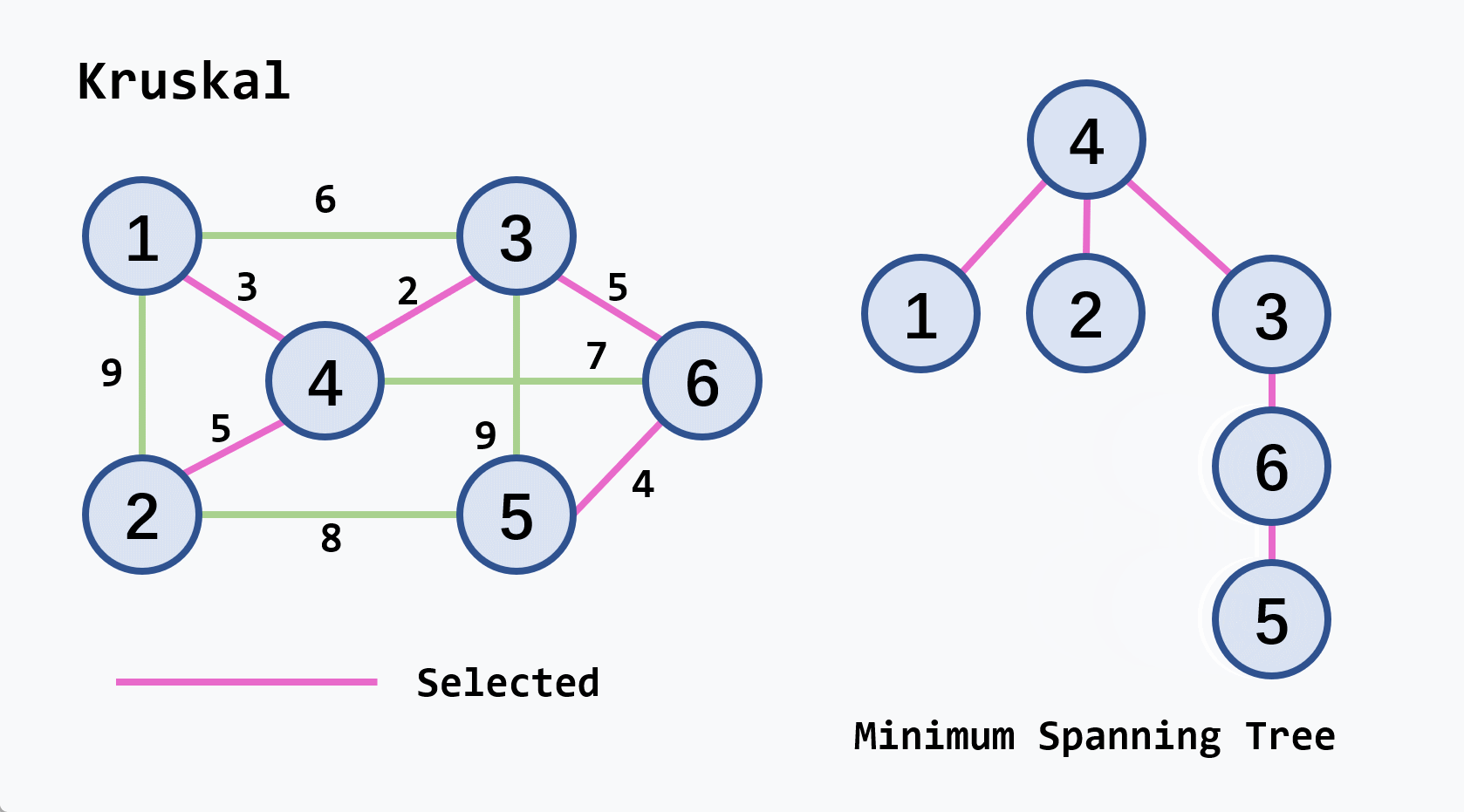
4. 最小生成树
1. 最小生成树
- 生成树的代价:设
- 最小生成树
- 最小生成树构造准则
- 尽可能用网络中权值最小的边
- 必须使用且仅使用
- 不能使用产生回路的边
2.
-
基本思想:从连通网络
-
注意
- 若候选轻权边集中的轻权边不止一条,可任选其中的一条扩充到生成树中
- 连通图的最小生成树不一定是唯一的,但它们的权相等
- 设连通网络有
-
算法
3.
-
基本思想:设有一个有
-
算法
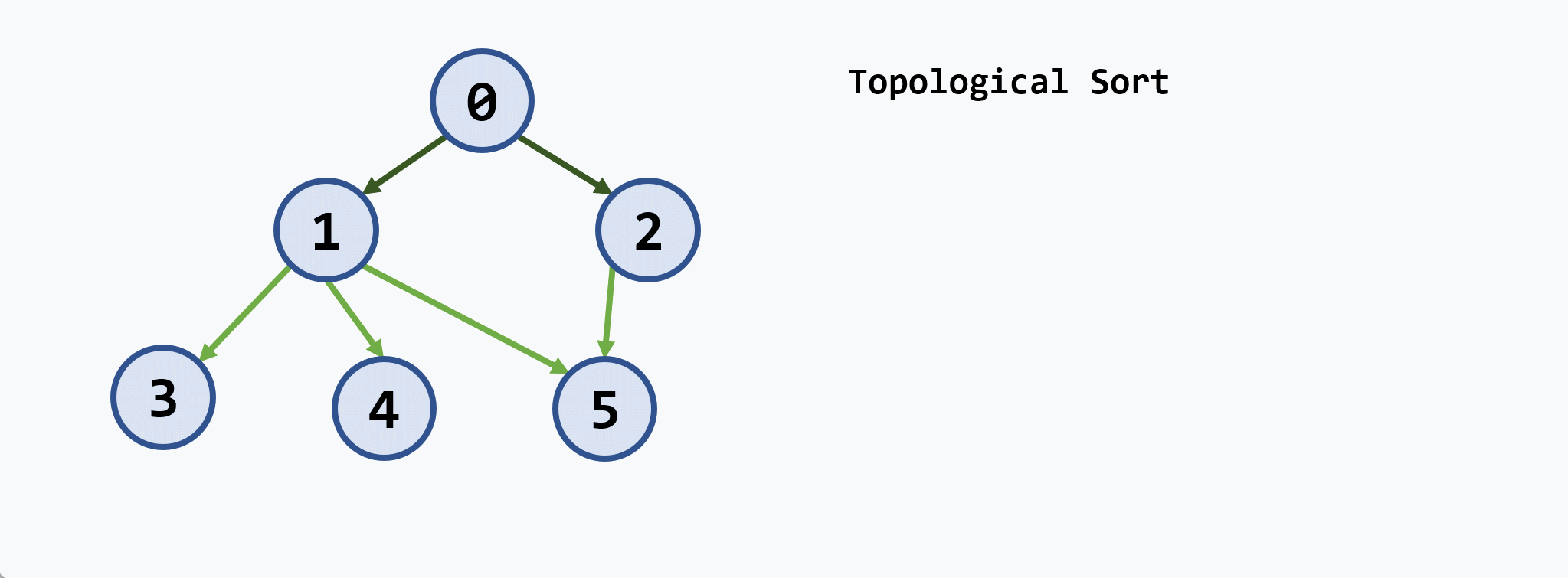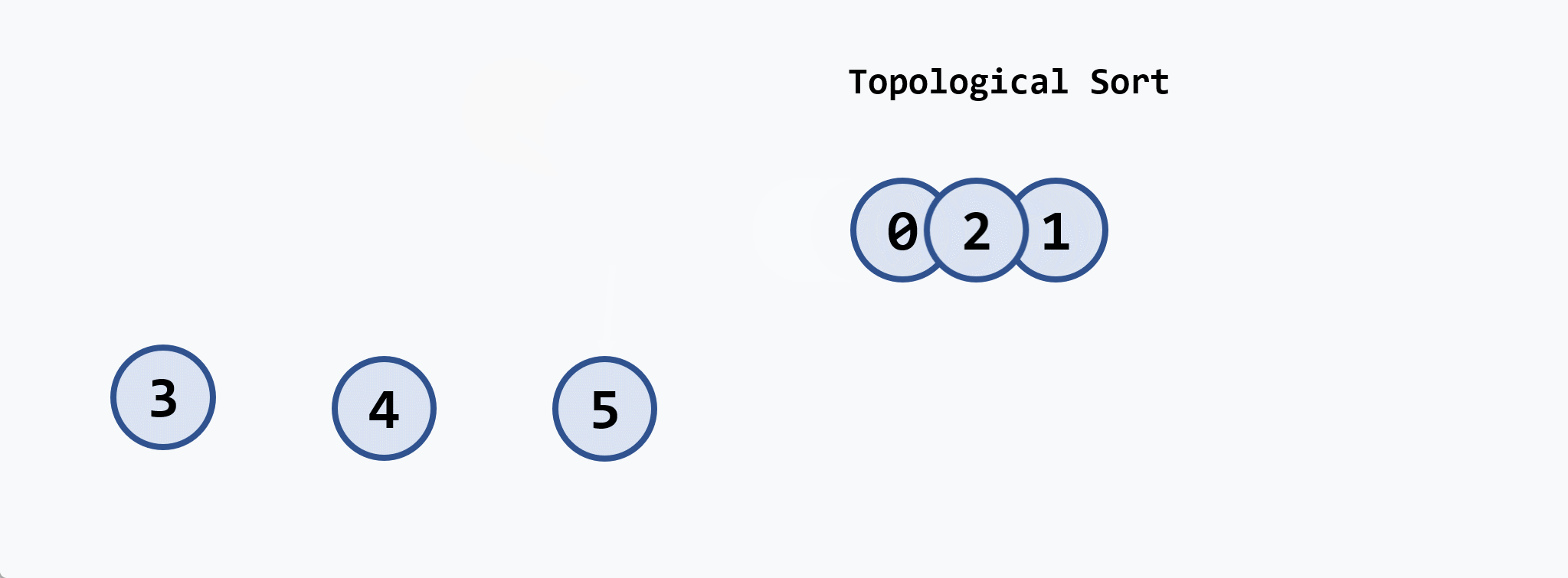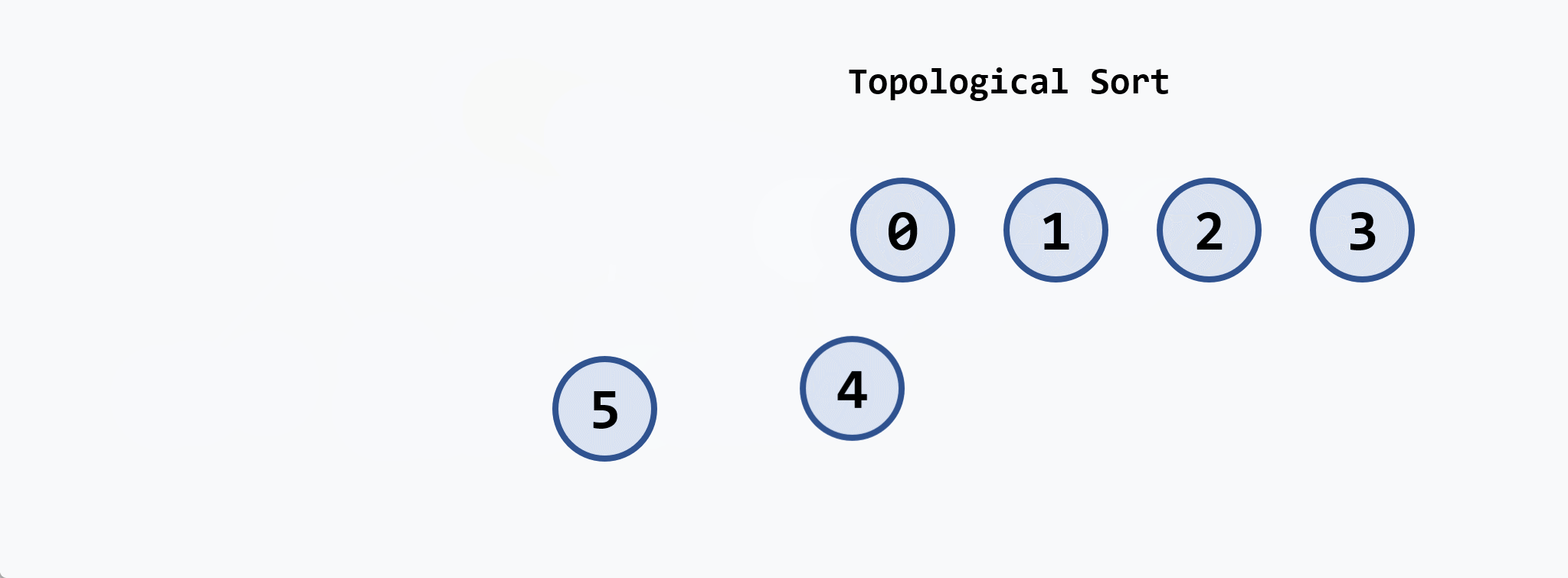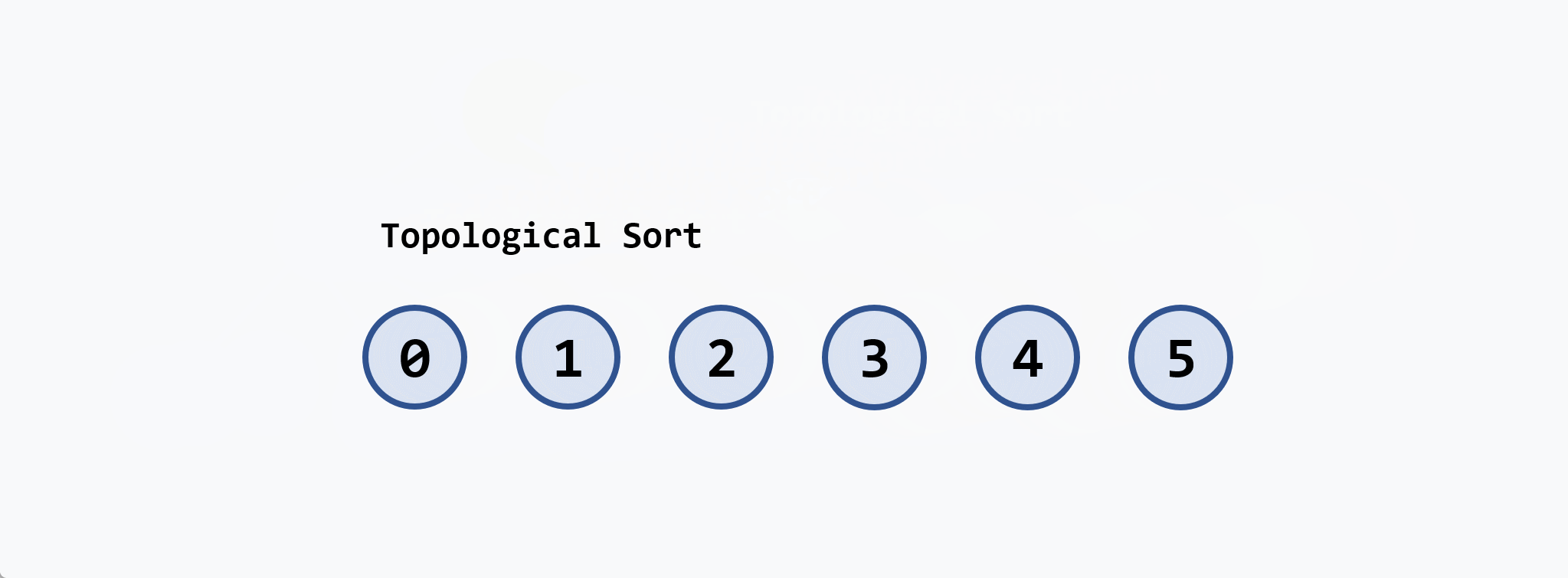
5. 拓扑排序
1.
- 如果AOV网络中存在有向环,此
- 拓扑序列: 即将各个顶点 (代表各个活动)排列成一个线性有序的序列,使得所有弧尾结点都排在弧头结点的前面
- 拓扑排序:构造
2. 拓扑排序
-
基本思想:在
-
算法
6.
1.
- 意义
- 完成整个工程至少需要多少时间(假设网络中没有环)
- 为缩短完成工程所需的时间, 应当加快哪些活动
- 源点与汇点:在
- 关键路径:完成整个工程所需的时间取决于从源点到汇点的最长路径长度,即在这条路径上所有活动的持续时间之和,这条路径长度最长的路径就叫做关键路径
- 关键活动:关键路径上的活动为 关键活动
2. 关键路径求解算法
-
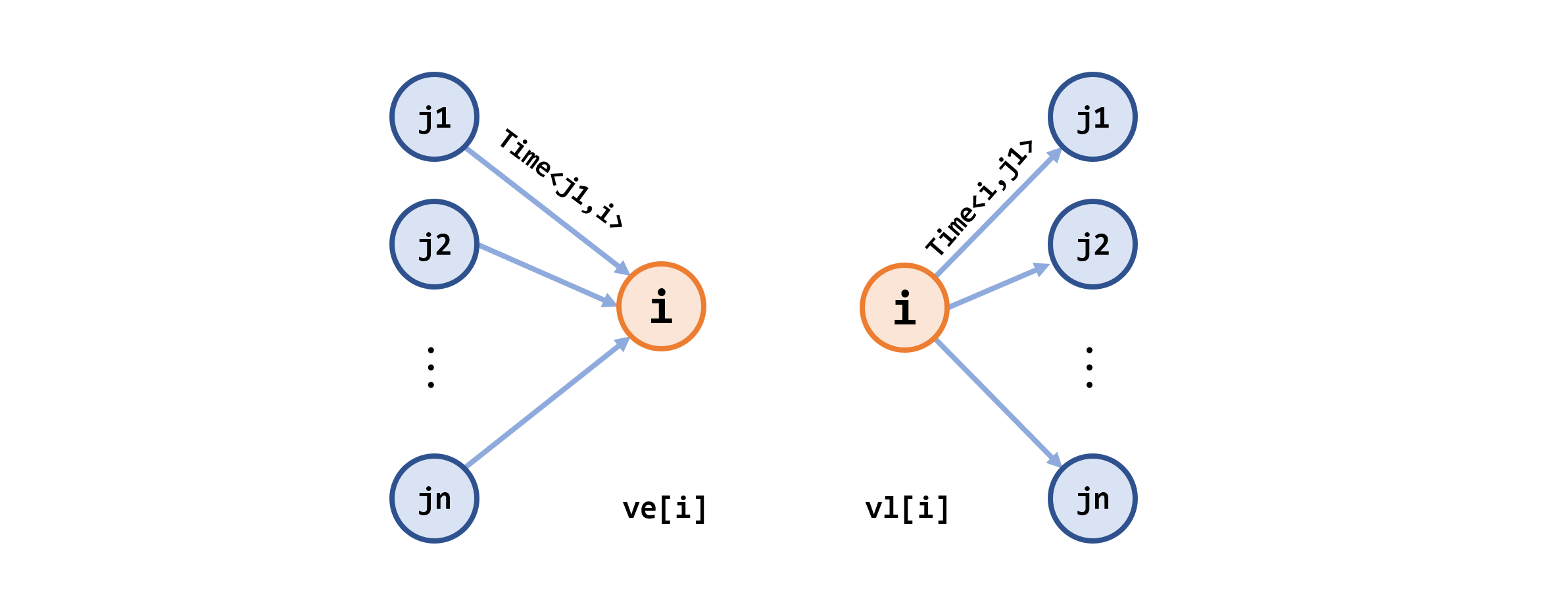
事件最早可能开始的时间
ve[i] -
事件最迟允许发生的时间
vl[i]- 概念:在保证汇点
ve[n-1]时刻完成的前提下,事件 - 算法:从
vl[n-1]=ve[n-1]开始开始反推,vl[i] = min{vl[j] - time<vi, vj>}
- 概念:在保证汇点
-
活动开始的最早时间
e[k]- 概念:设活动
ak在带权有向边<vi, vj>上,其持续时间为time<vi, vj>,其最早发生时间e[k]=ve[i]
- 概念:设活动
-
活动最迟允许开始时间
l[k]- 概念:
l[k]是在不会引起时间延误的前提下, 该活动允许的最迟开始时间,l[k] = vl[j] - time<i, j>
- 概念:
-
时间余量
l[k]-e[k]:表示活动ak的最早可能开始时间和最迟允许开始时间的时间余量。l[k] == e[k]表示活动ak是没有时间余量的关键活动 -
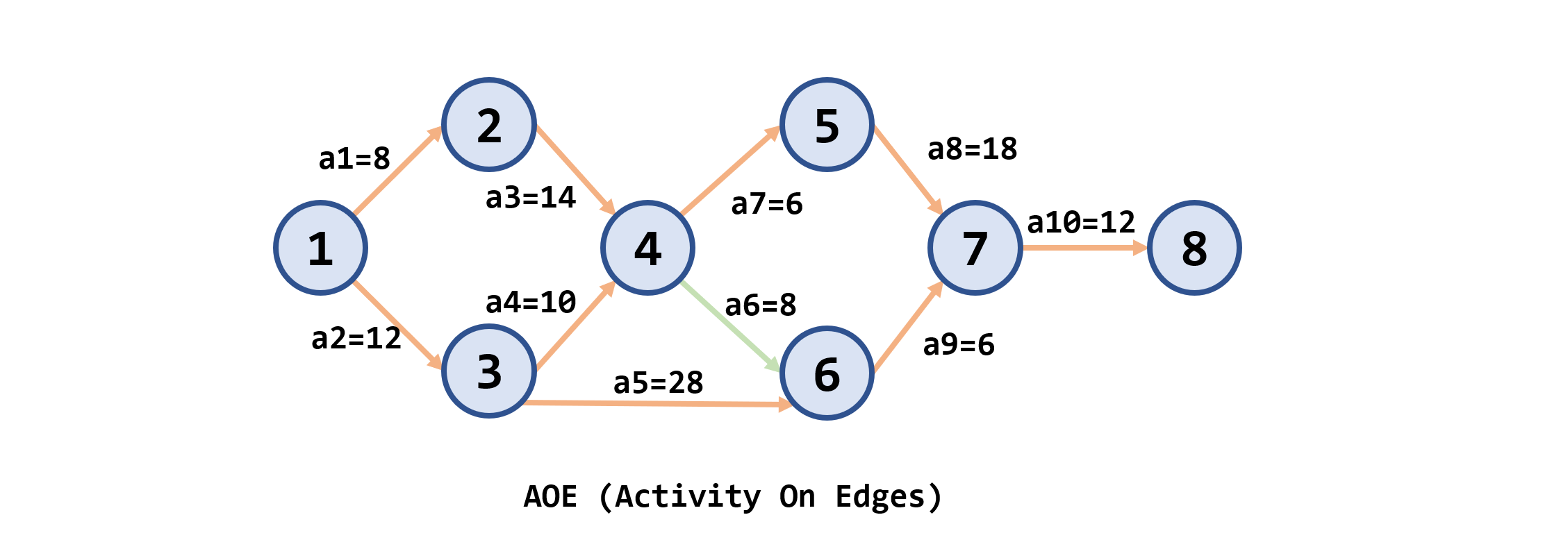
vertex1 2 3 4 5 6 7 8 ve0 8 12 22 28 40 46 58 vl0 8 12 22 28 40 46 58 由公式计算出:
edge(activity)1 2 3 4 5 6 7 8 9 e0 8 12 12 22 22 28 40 46 l0 8 12 12 22 32 28 40 46 因此除了
a6不是关键活动,其他都是,因此得出关键路径 -
算法
7. 最短路径
1. 最短路径问题
- 最短路径:如果图是一个带权图,则路径长度为路径上各边的权值之和,两个顶点之间的路径长度最短的路径为两个点之间的最短路径,其长度是 最短路径长度
- 算法
2.
-
基本思想:按路径长度的递增次序, 逐步产生最短路径的算法。首先求出长度最短的一条最短路径,再参照它求出长度次短的一条最短路径,依次类推,直到从顶点v到其它各顶点的最短路径全部求出为止
-
示例:计算从
v4顶点到各顶点的最短路径(pre表示连接的前驱点,dist表示当前的最短路径长度)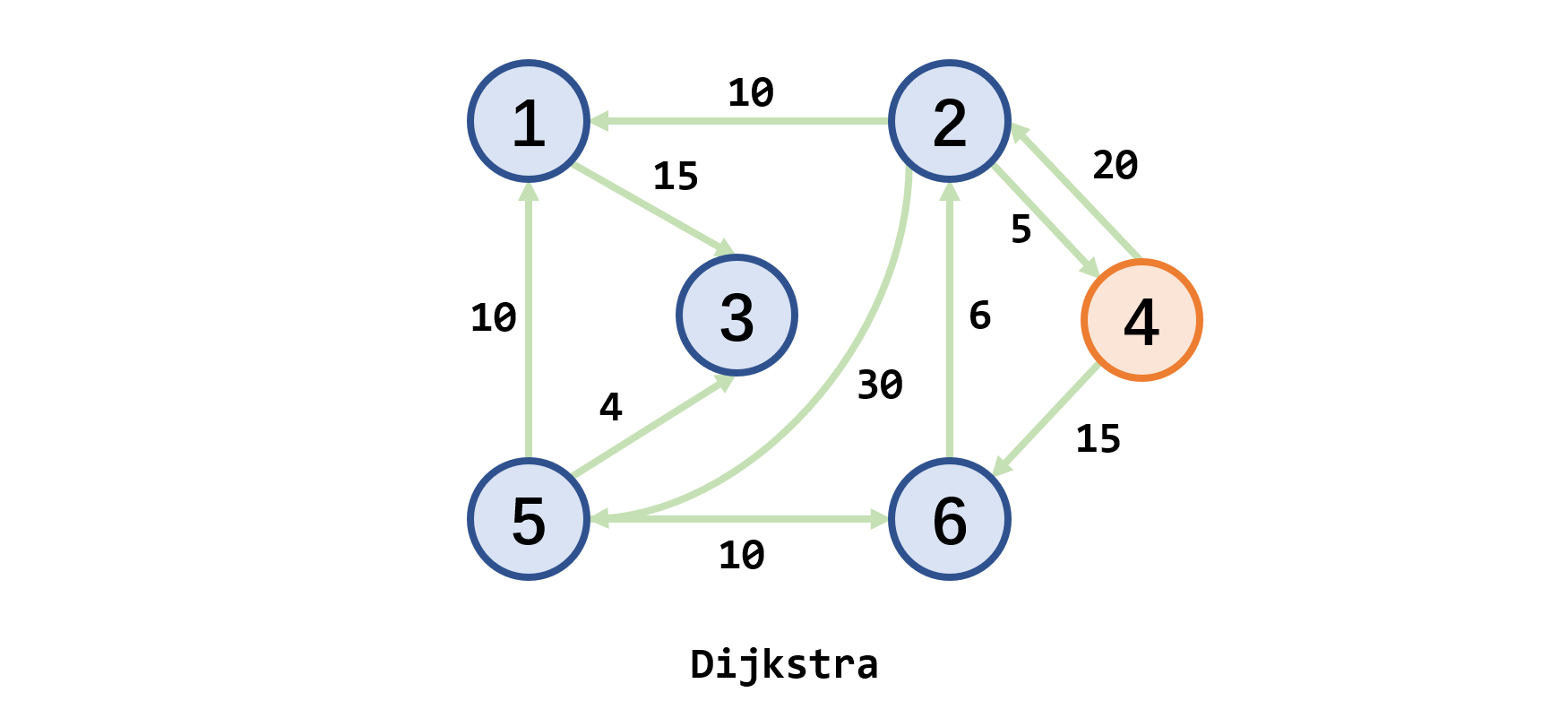
v1v2v3v4v5v6dist20 0 15 prev4v4v4v4v4v4dist30 20 ✔️ 15 prev2v4v4✔️ v4v4dist30 20 45 ✔️ 50 ✔️ prev2v4v1✔️ v2✔️ dist30 ✔️ 45 ✔️ 50 ✔️ prev2✔️ v1✔️ v2✔️ dist✔️ ✔️ 45 ✔️ 50 ✔️ pre✔️ ✔️ v1✔️ v2✔️ dist✔️ ✔️ ✔️ ✔️ 50 ✔️ pre✔️ ✔️ ✔️ ✔️ v2✔️ dist✔️ ✔️ ✔️ ✔️ ✔️ ✔️ pre✔️ ✔️ ✔️ ✔️ ✔️ ✔️ 因此从顶点
v4出发到其余顶点的最短路径及长度vertexlengthpathv130 v4->v2->v1v220 v4->v2v345 v4->v2->v1->v3v40 v4v550 v4->v2->v5v615 v4->v6 -
算法
- 基于
dist[]数组的 - 使用一个小根堆来寻找未确定节点中与起点距离最近的点的
- 基于
3.
- 基本思想:从初始的邻接矩阵
- 递推公式:
- 路径记录:显然,
path[i][j],是从i到j的中间点序号不大于path[i][j]的值就可以得到从i到j的最短路径上的各个顶点 - 算法
__EOF__
本文链接:https://www.cnblogs.com/RadiumGalaxy/p/17069446.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!

 图、搜索、并查集等
图、搜索、并查集等


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话