07 树 | 数据结构与算法
1. 树
1. 树的定义
-
树 (
- 有且只有一个特殊的称为树的 根(
- 若
- 有且只有一个特殊的称为树的 根(
-
树的具体概念
- 结点的度:结点的子树个数
- 树的度:树中结点的度的 最大值
- 叶结点:度为零的结点
- 双亲结点:某个结点的子树的双亲
- 兄弟结点:具有同一双亲结点的所有结点
- 路径和路径长度:如果树的结点序列
- 祖先和子孙:在树中,如果有一条路径从
x到y,那么x就是y的祖先,y是x的子孙 - 结点的层数:根节点的层数为1,对于任意结点,若结点在第k层,则它的孩子结点在k+1层
- 树的深度:树中所有结点的最大层数
-
树的分类
- 有序树:子树的次序不能交换
- 无序树:子树的次序可以交换
- 森林:互不相交的树的集合
2. 树的基本操作
- 求根节点
- 求指定节点的双亲结点
- 求指定节点的某一个孩子节点
- 插入子树或者结点
- 删除子树或者结点
- 树的遍历:根据某种规则,按照一定的顺序访问树中的每一个结点,使得每个结点被访问且仅被访问一次
- 前序遍历:访问根结点,再依次前序遍历树的各子树
- 后序遍历:依次后序遍历树的各子树,再访问根结点
- 前序遍历一棵树等价于前序遍历该树对应的二叉树,后序遍历一棵树等价于中序遍历该树对应的二叉树
- 前序遍历:访问根结点,再依次前序遍历树的各子树
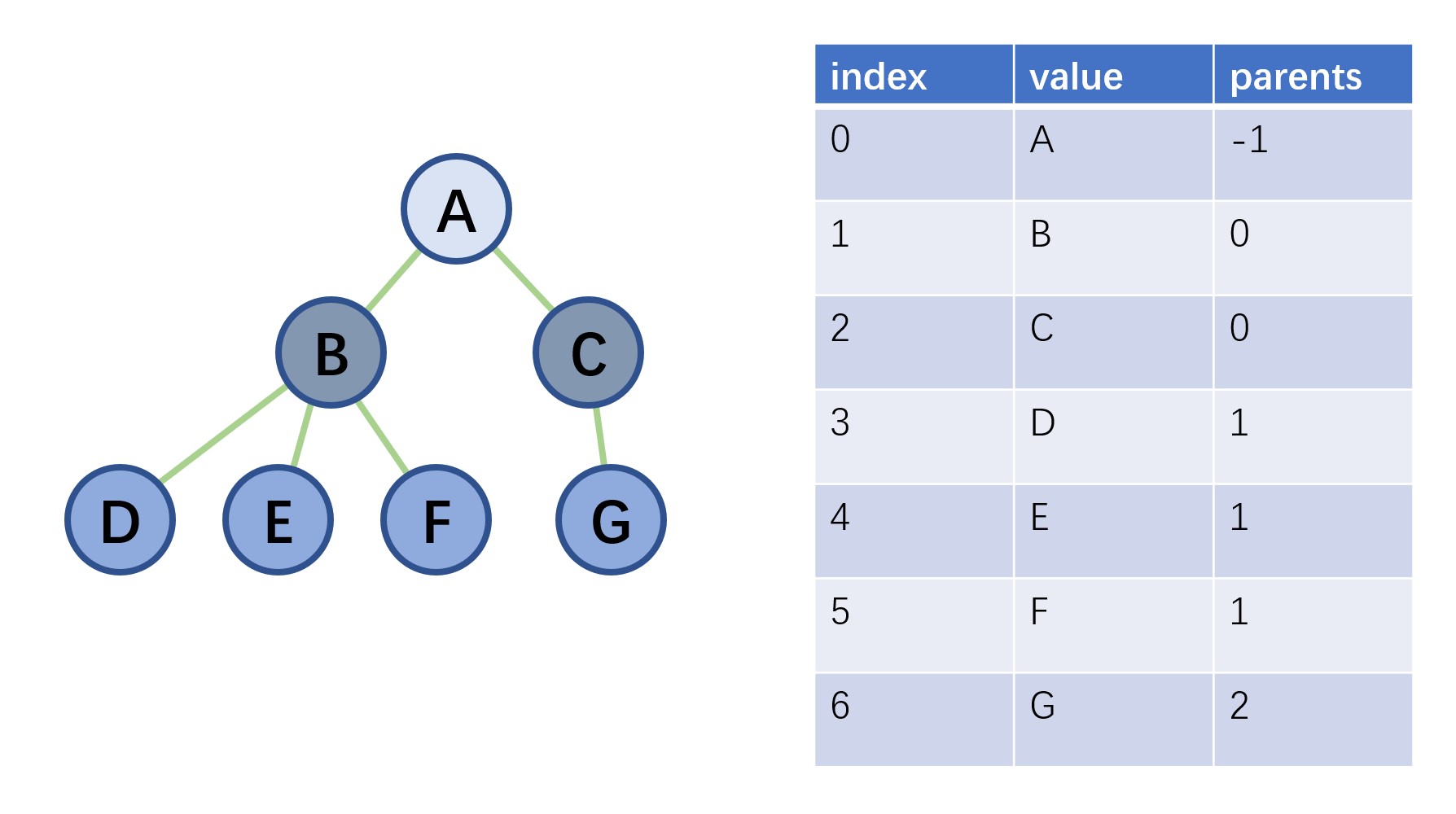
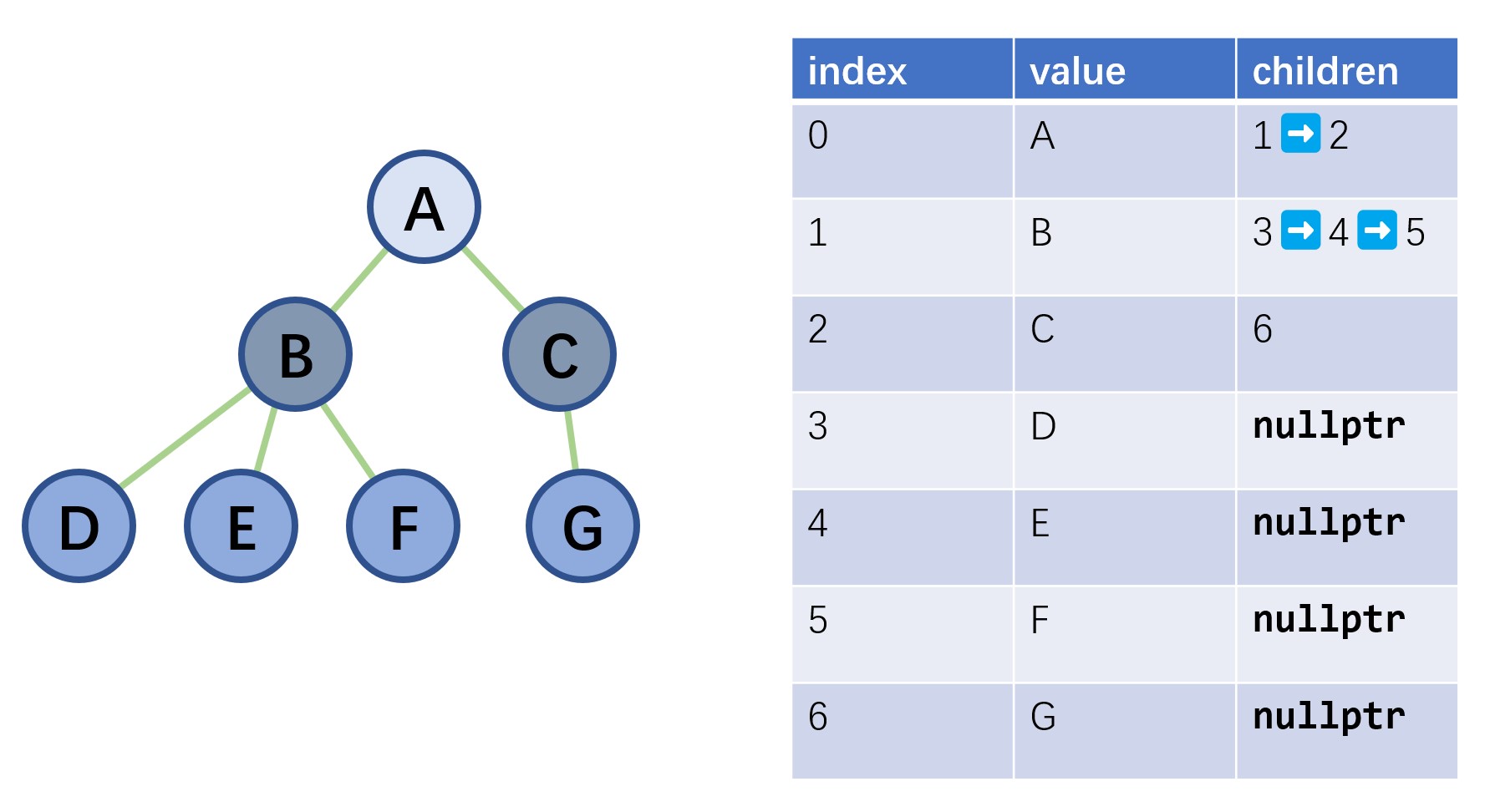
3. 存储设计
2. 二叉树
1. 二叉树的定义
- 二叉树:二叉树是一个是
- 结构特点
- 每个节点最多只有两颗子树,即结点的都不超过2
- 子树有左右之分,顺序不能颠倒
- 即使只有一棵子树,也有 左右之分
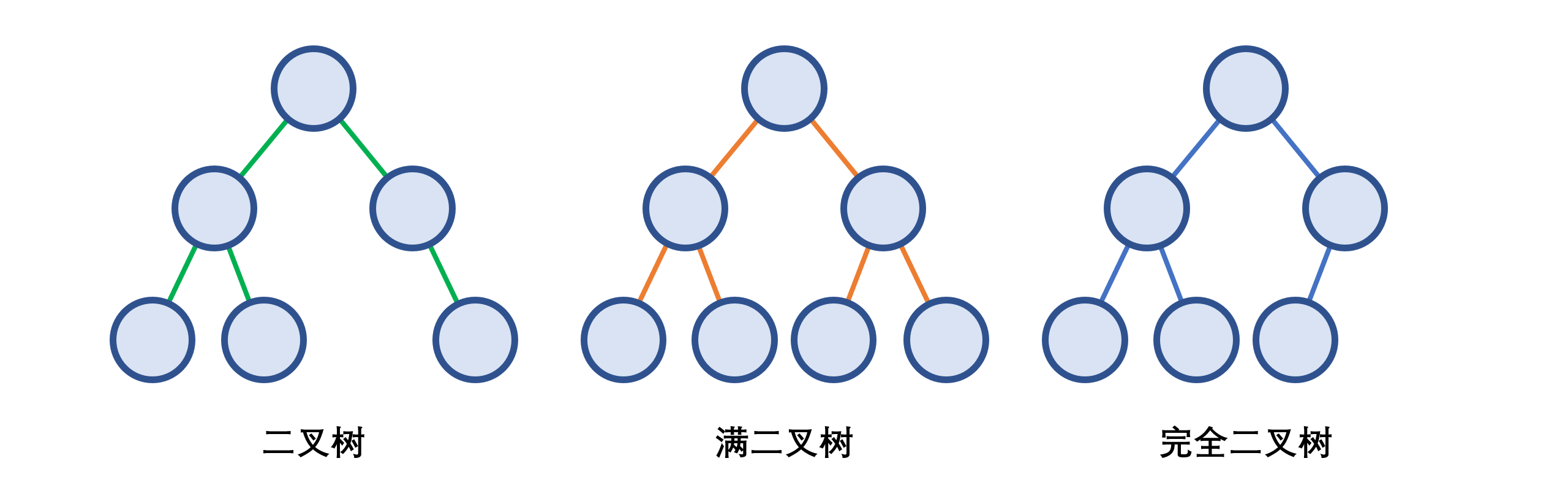
- 满二叉树
- 定义:高度为
- 结构特点
- 分支节点都有两棵二叉树
- 叶子节点都在最后一层
- 在所有二叉树中,满二叉树的结点数量,分支节点数量和叶子节点数量是 最多的
- 定义:高度为
- 完全二叉树
2. 二叉树的性质
- 若二叉树的层次从1开始,那么在二叉树的第
- 高度为
- 对任何一棵二叉树, 如果其叶结点个数为
- 具有
- 完全二叉树的连续存储设计的下标特点:如果将一棵有
- 若
- 若
- 若
- 若
- 若
- 若
- 若
- 二叉树的存储设计
4. 二叉树的遍历
- 前序遍历
- 递归
- 迭代
- 递归
- 中序遍历
- 递归
- 迭代
- 递归
- 后序遍历
- 递归
- 迭代
- 递归
- 层序遍历
5. 二叉树的操作
- 统计叶子节点数:任意遍历的时候将访问改为计数器加一即可
- 求二叉树的高度
- 由先序遍历和中序遍历可 唯一 确定一棵二叉树
3. 线索树
1. 线索树
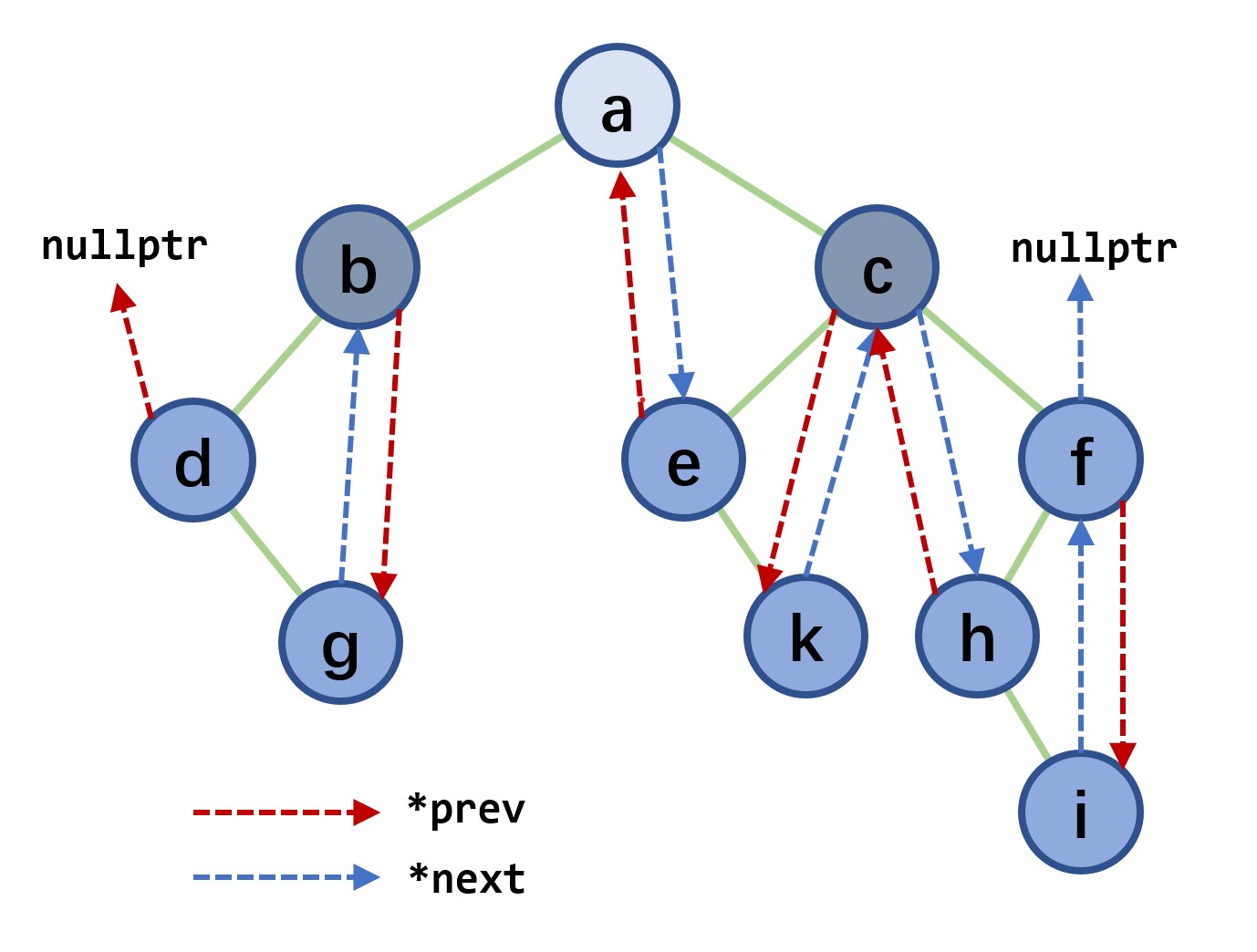
- 目的:遍历二叉树是按一定的规则将树中的结点排列成一个线性序列,即是对非线性结构的线性化操作。线索树可以存储遍历过程中动态得到的每个结点的直接前驱和直接后继
- 原理:空闲指针的利用:设一棵二叉树有
n个结点,则有n-1条边(指针连线) ,而n个结点共有2n个指针域(*left和*right) ,显然有n+1个空闲指针域未用。则可以利用这些空闲的指针域来存放结点的直接前驱和直接后继信息 - 线索树定义
- 如果结点有左孩子,那么
*left指向左孩子,否则指向直接前驱 - 如果结点有右孩子,那么
*right指向右孩子,否则指向直接后继 - 为了避免混淆,增加2个标志域
leftTag,rightTag,等于0的时候和指示孩子,等于1的时候指示前驱后继
- 如果结点有左孩子,那么
- 线索化二叉树
-
线索树:遍历二叉树是按一定的规则将树中的结点排列成一个 线性序列,即是对非线性结构的线性化操作。在树中直接存储遍历过程中动态得到的每个结点的直接前驱和直接后继(第一个和最后一个除外)的信息就是线索化二叉树;设一棵二叉树有
-
线索树的指针域:
- 如果节点有左孩子,则
left指向左孩子,否则指向其直接前驱 - 如果节点有右孩子,则
right指向右孩子,否则指向其直接后继 - 加以改进:在指针域之中添加两个标志域
leftTag和rightTagleftTag == 1: *leftChild; leftTag == 0: *prevrightTag == 1: *rightChild; rightTag == 0: *next
- 如果节点有左孩子,则
-
- 寻找前驱:在当前结点的左子树的根的最右侧节点
- 寻找后继:在当前结点的右子树的根的最左侧节点
- 寻找前驱:在当前结点的左子树的根的最右侧节点
-
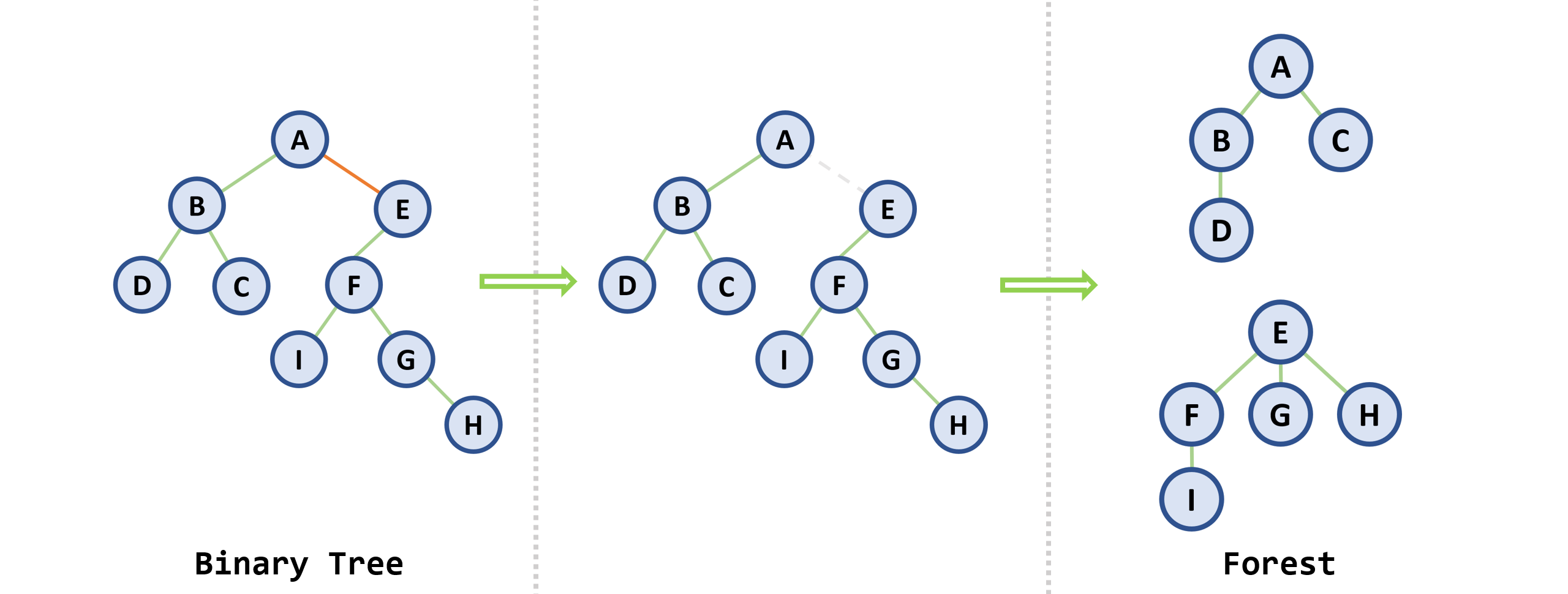
4. 森林与二叉树的转换
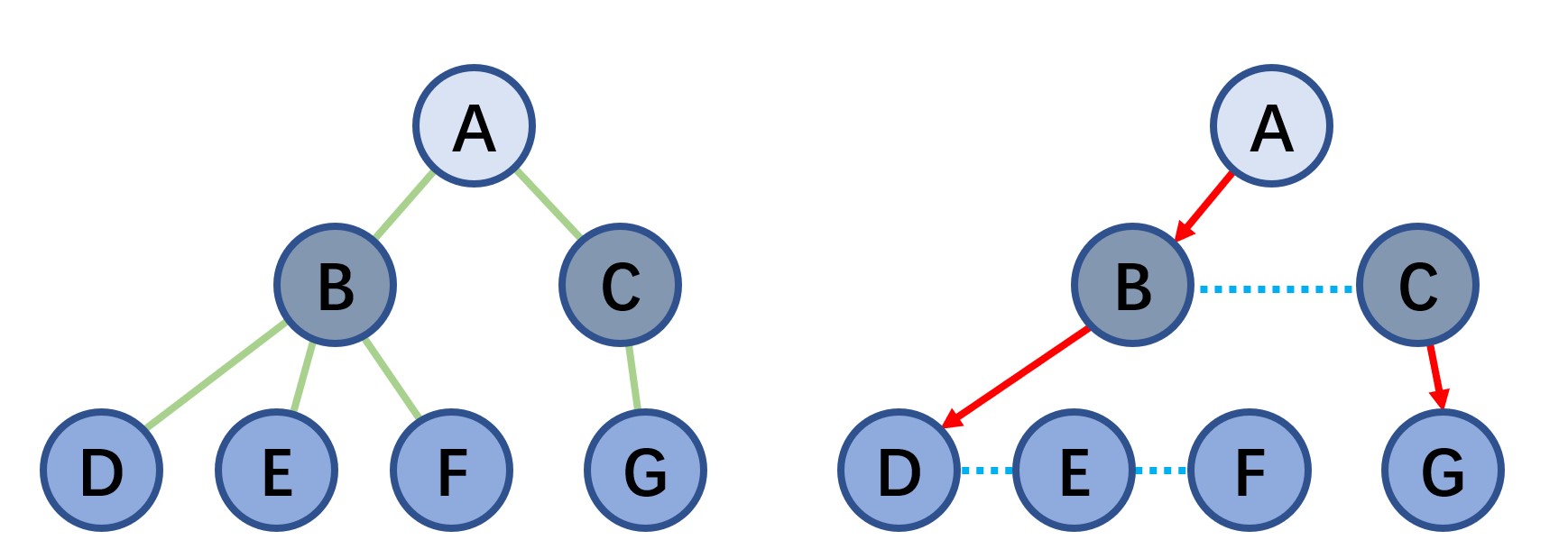
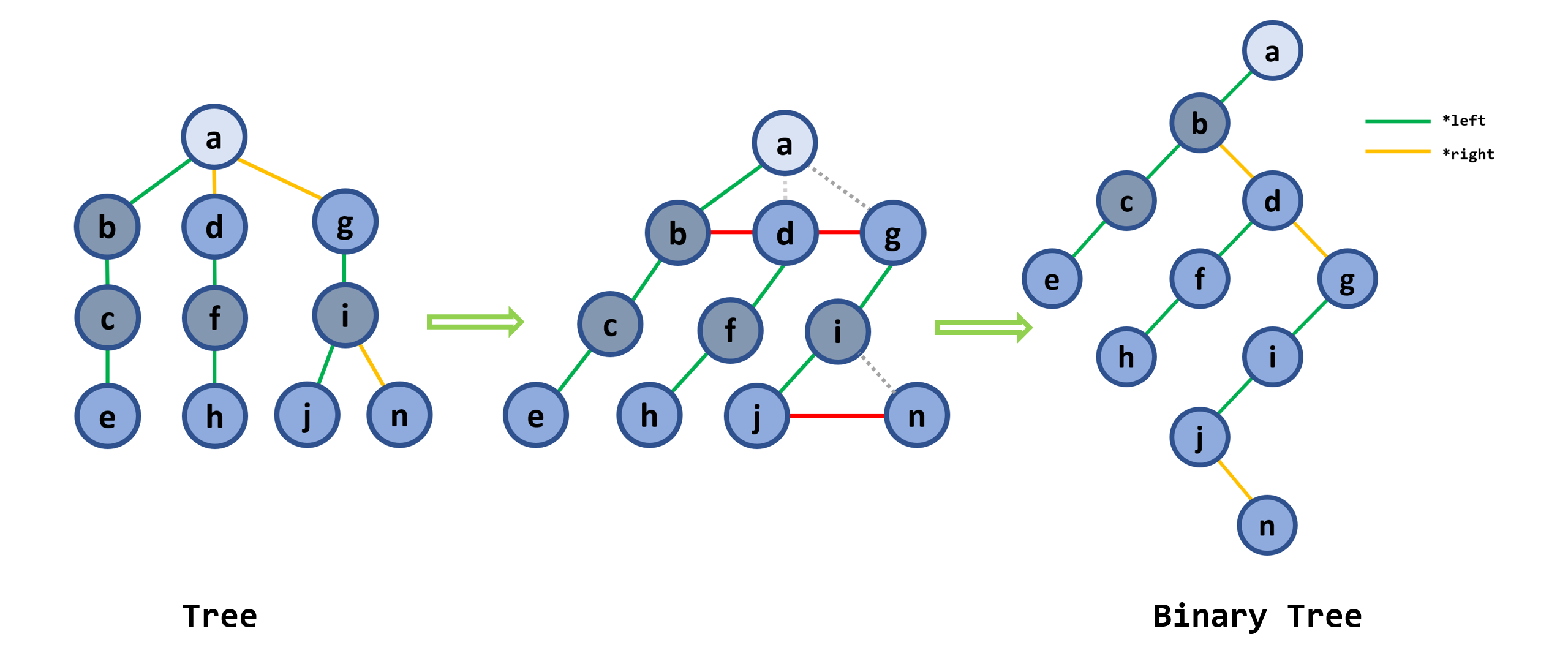
1. 树转换为二叉树
-
连线:在树的每层按从“左至右”的顺序在兄弟结点之间加虚线相连
-
删线:除最左的第一个子结点外,父结点与所有其它子结点的连线都去掉
-
性质
- 二叉树的根结点没有右子树,只有左子树
- 左子结点仍然是原来树中相应结点的左子结点,而所有沿右链往下的右子结点均是原来树中该结点的兄弟结点
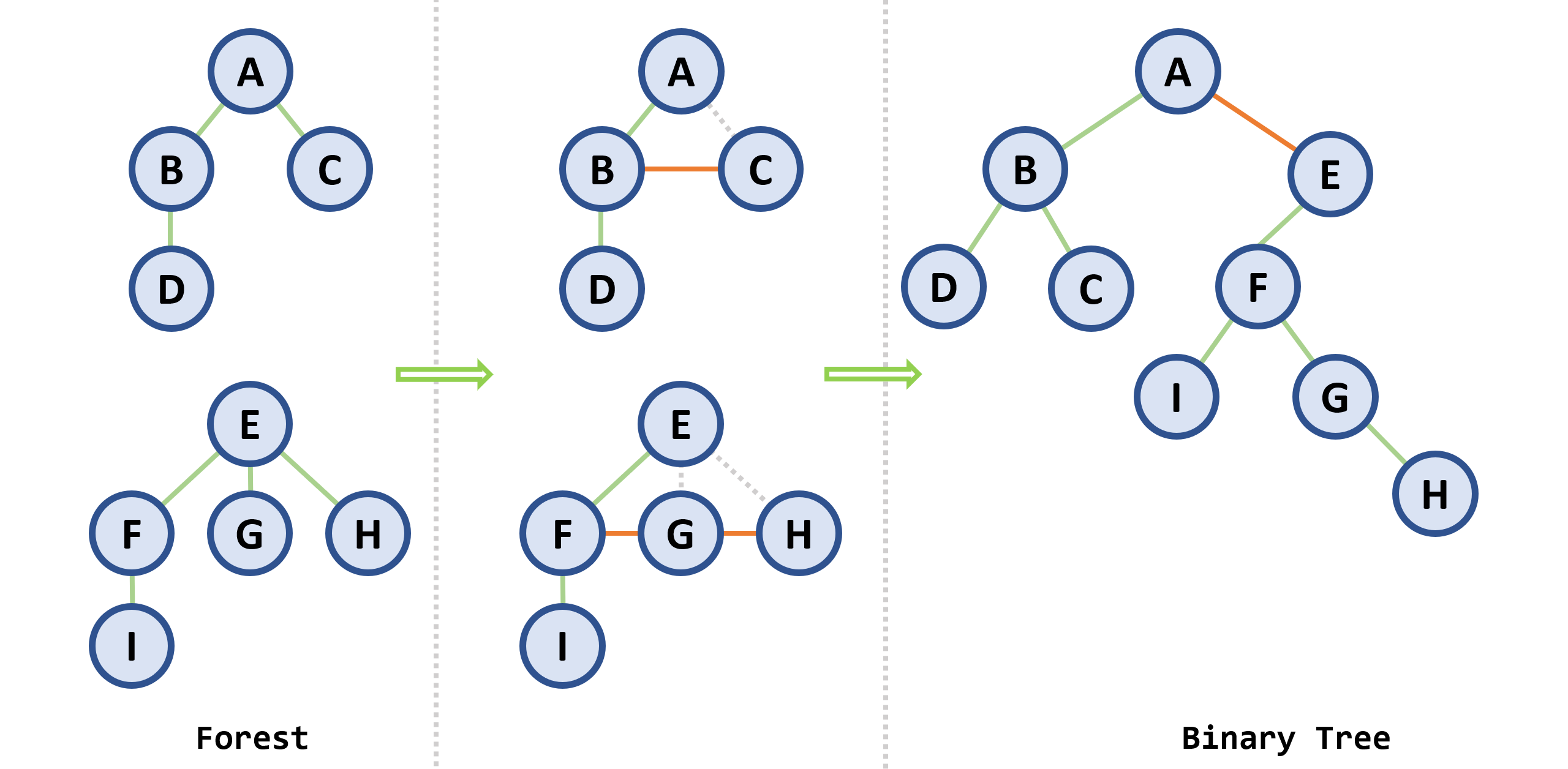
2. 森林转换为二叉树
- 若森林不空,则对应二叉树的根
root是Forest中第一棵树T1的根root(T1);其左子树为T1的子树;其右子树为T2,T3, ...,Tn,其中,T2,T3, ...,Tn是除T1外其它树构成的森林 - 转换步骤
3. 二叉树还原为森林
- 若二叉树不空,则
Forest中第一棵树T1的根为root;T1的根的子树森林{T11, T12, ..., T1m}是由root的左子树转换而来,Forest中除了T1之外其余的树组成的森林{ T2, T3, ..., Tn}是由root的右子树转换而成的森林 - 转换步骤
5. 哈夫曼树
1. 哈夫曼树
- 叶子节点的权值:对叶子节点赋予一个有意义的数值
- 二叉树的带权路径长度:设二叉树具有
- 哈夫曼树:带权路径长度 最短 的二叉树
- 哈夫曼树的特点
- 树中没有分支为一的节点
- 哈夫曼树的形态 不唯一
- 权值较大的节点离根较近,权值较小的结点离根较远
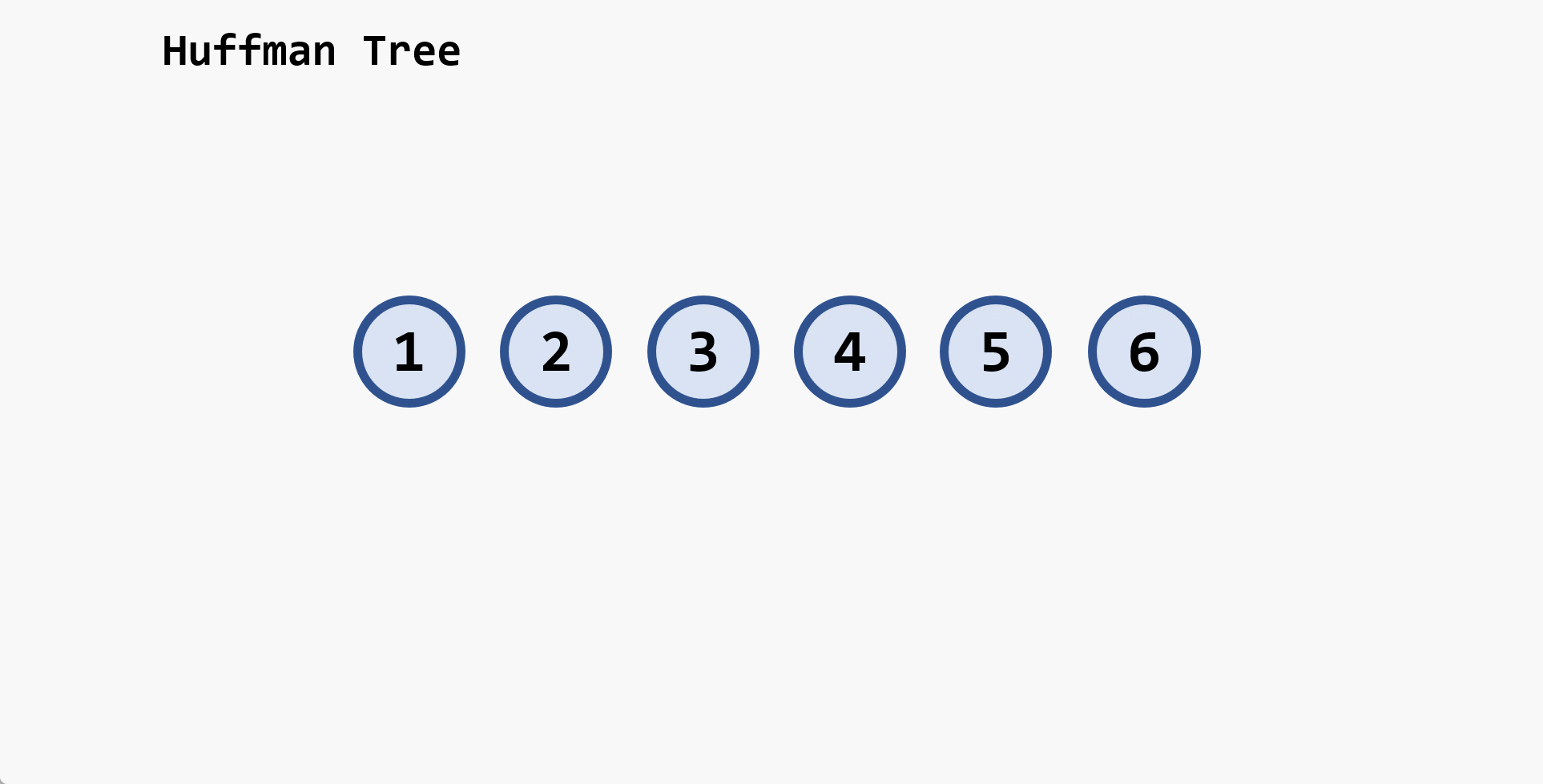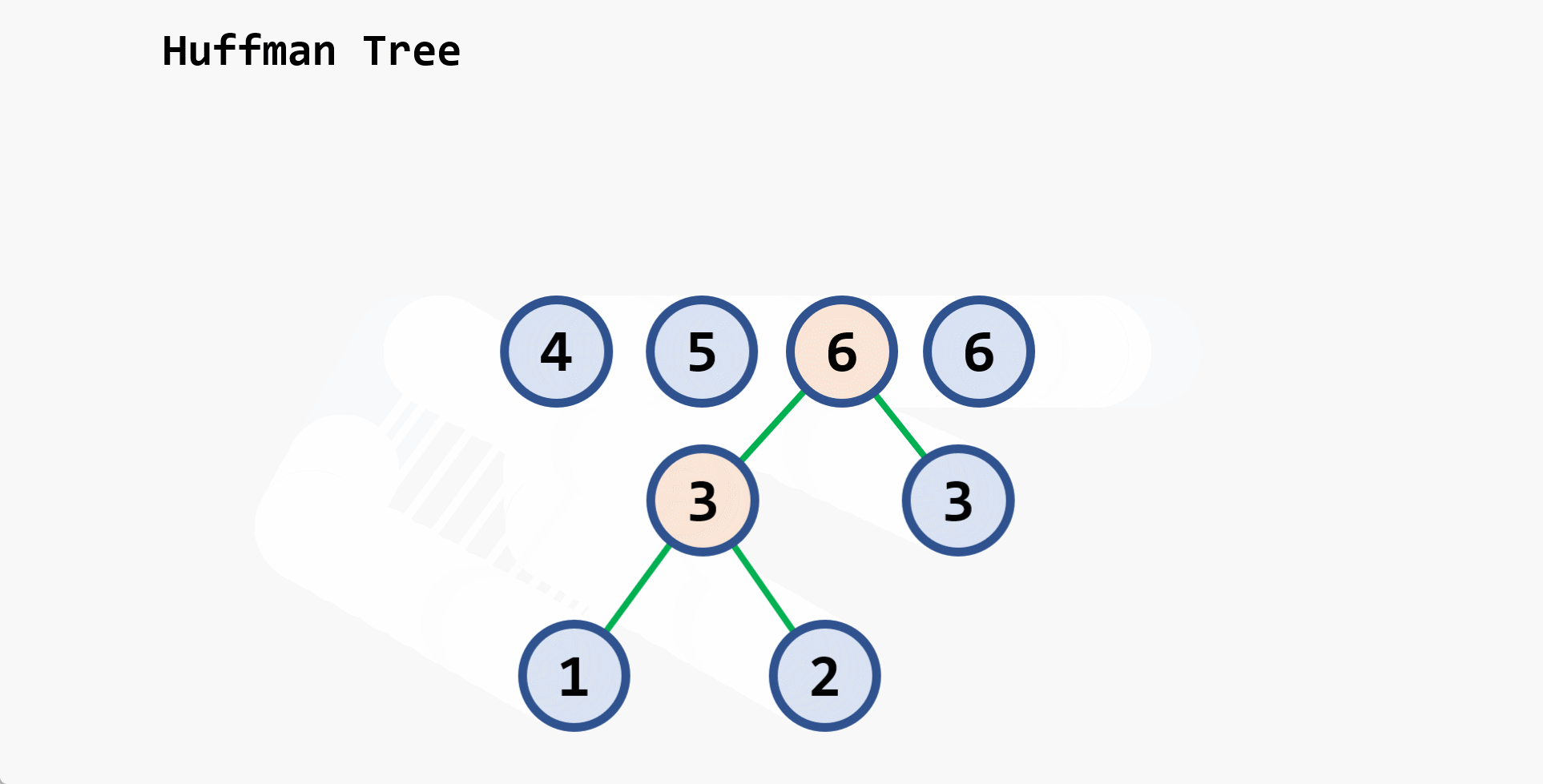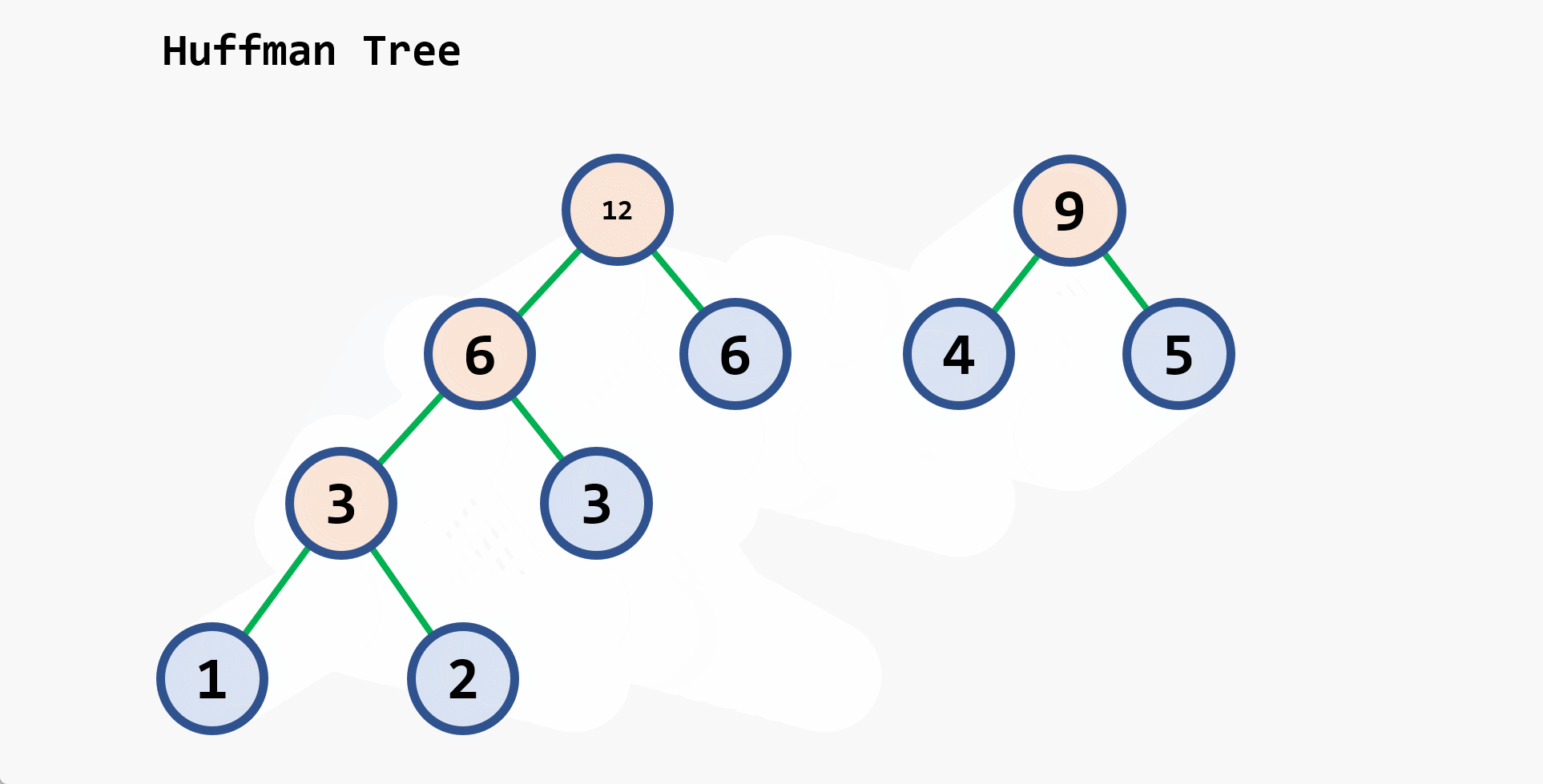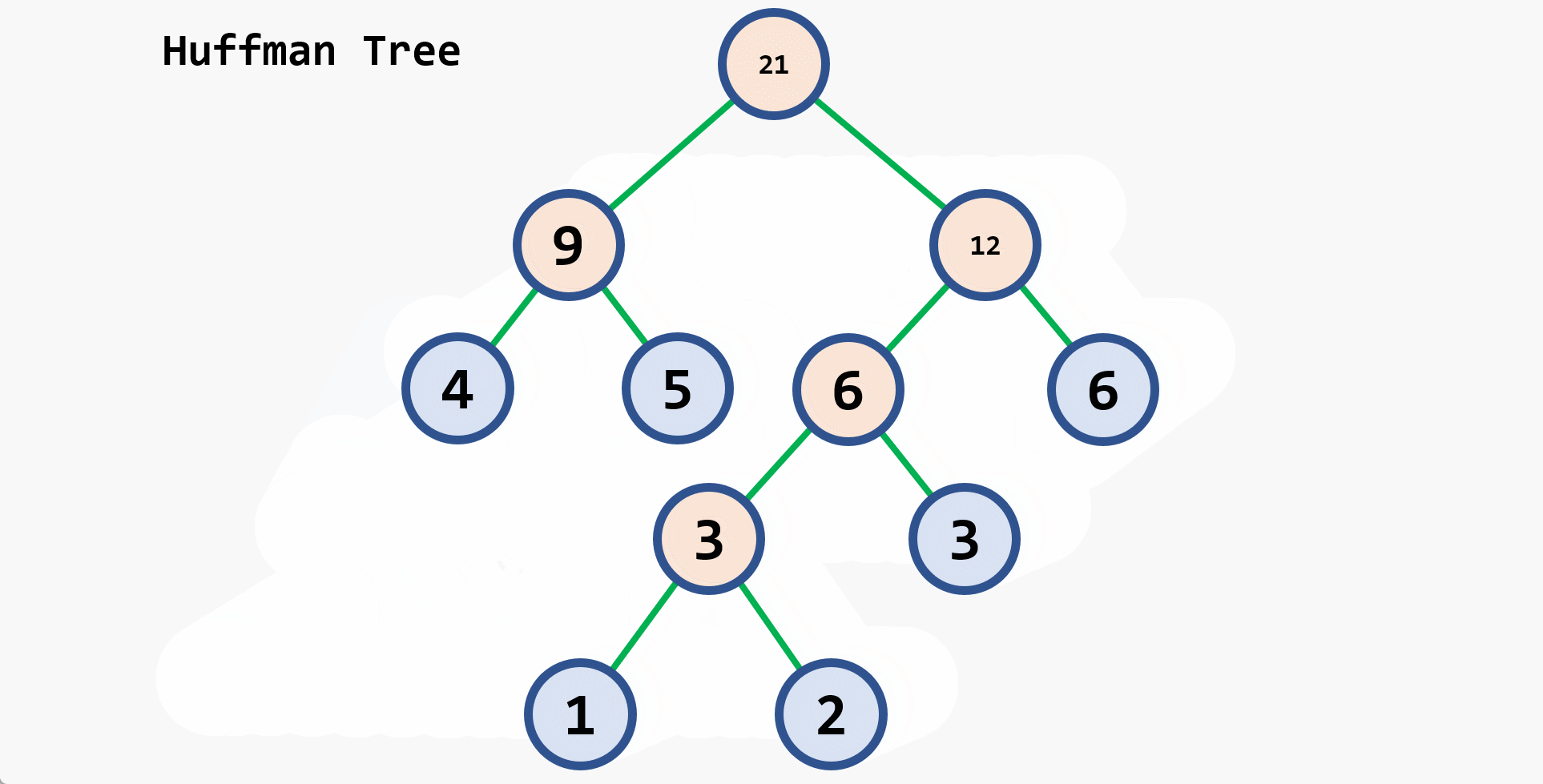
2. 构造哈夫曼树
-
步骤
- 将给定的
{w1, w2, ..., wn}作为{T1, T2, ..., Tn},其中每棵二叉树只有一个根结点 - 在森林中选取两棵根结点权值 最小 的二叉树作为左右子树构造一棵新二叉树,新二叉树的根结点权值为这两棵树根的 权值之和
- 在森林中,将上面选择的这两棵根权值最小的二叉树从森林中删除,并将刚刚新构造的二叉树加入到森林中
- 重复上面(2)和(3),直到森林中只有一棵二叉树为止。这棵二叉树就是哈夫曼树
- 将给定的
-
算法
- 构建哈夫曼树
- 计算
3. 哈夫曼编码
-
背景:在电报收发等数据通讯中,常需要将传送的文字转换成由二进制字符0、1组成的字符串来传输。为了使收发的速度提高,就要求电文编码要尽可能地短
-
前缀码:如果一组编码中任意一个编码 都不是 其他任何一个编码的前缀,则称这种编码具有前缀性,简称 前缀码
- 等长编码是前缀码
- 变长编码为了使得译码不具有二义性,需要具备前缀性
-
平均编码长度:设每个对象
-
最优前缀码:使得平均编码长度 最短 的前缀编码为最优前缀码
-
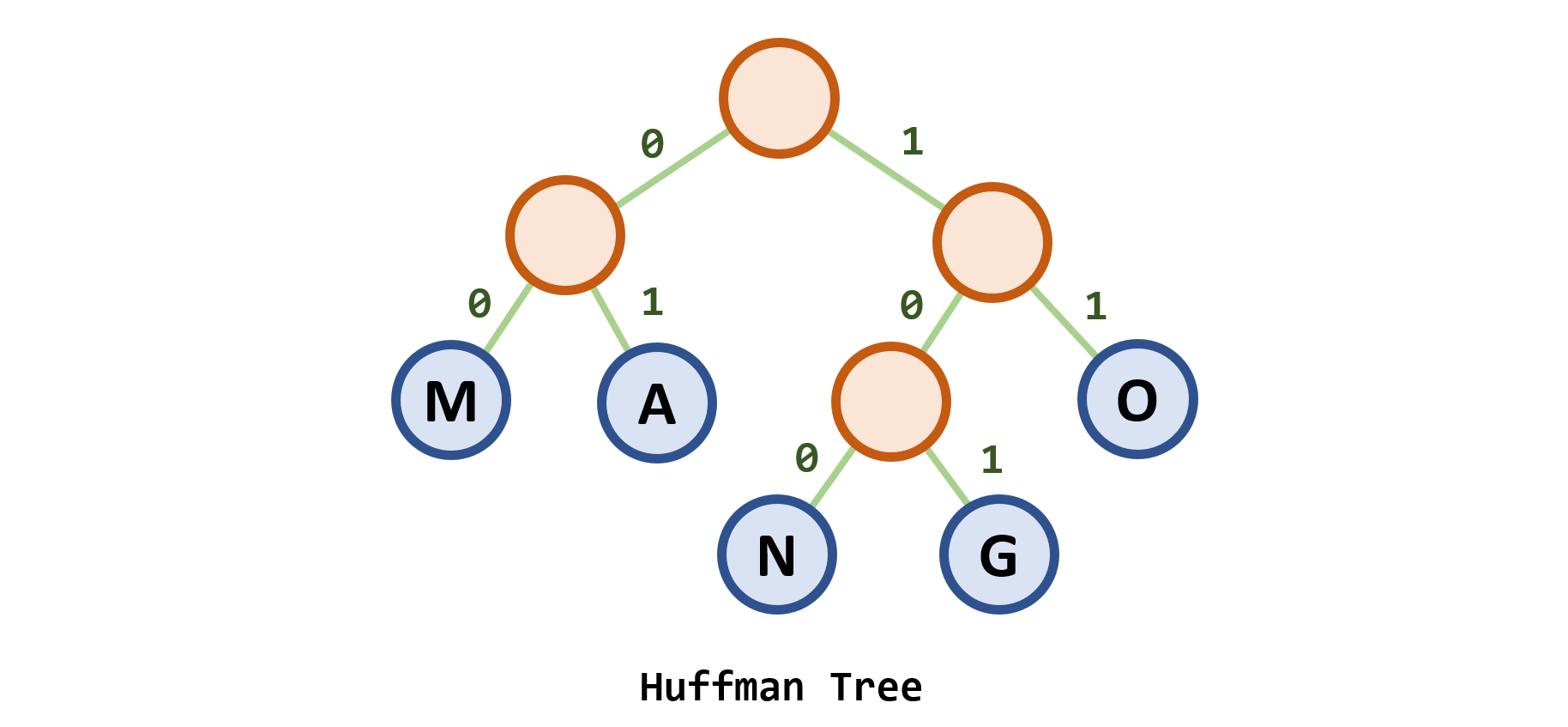
哈夫曼编码:利用哈夫曼树,左支为0,右支为1,从 根到叶子的01序列就是 哈夫曼编码
- 一定具有 前缀性
- 最小冗余码
- 出现概率大的对象对于码长 短
- 编码不唯一
-
charM A N G O code00 01 100 101 11 -
哈夫曼译码算法
6. 二叉查找树
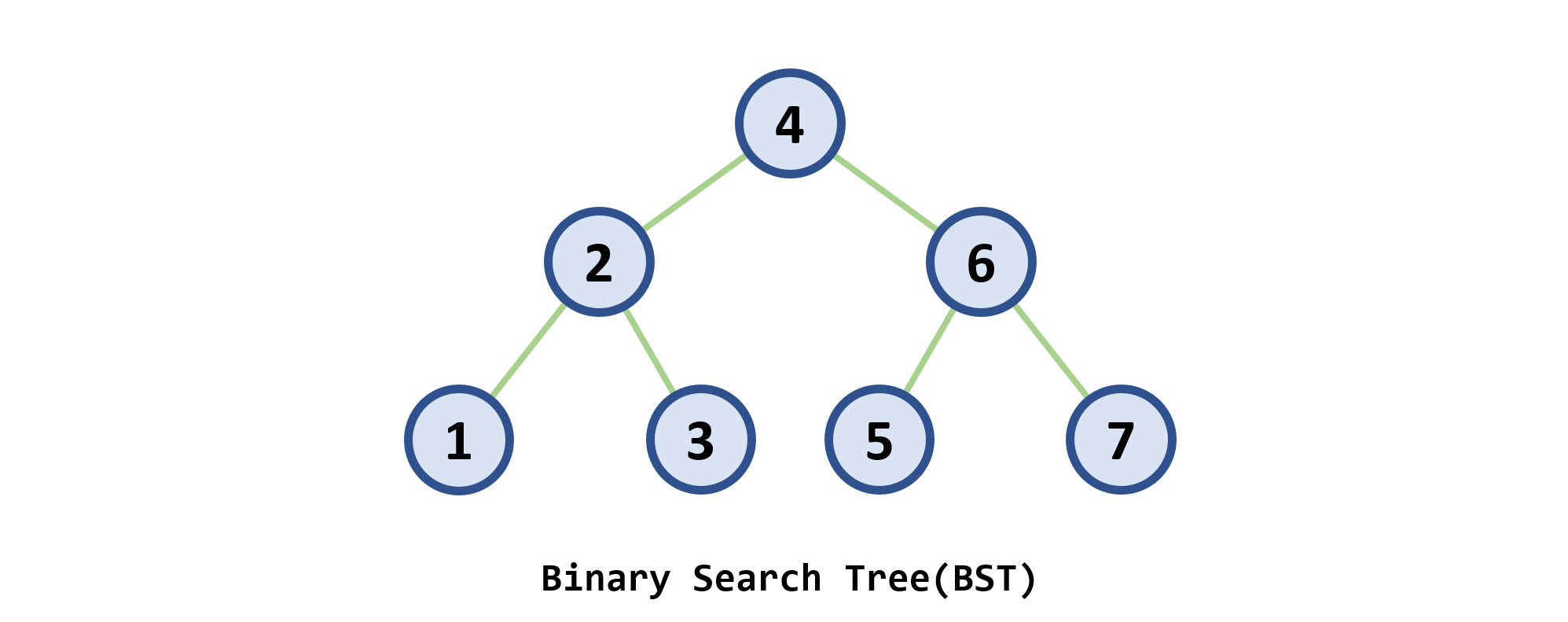
1. 二叉查找树
-
二叉查找树:二叉查找树(二叉排序树) 或者是一棵空树,或者是具有下列性质的二叉树
-
二叉查找树的特点
- 任意一个节点的关键字都 大于 其左子树的任意节点,小于 其右子树的任意节点
- 按 中序遍历 二叉查找树所得到的中序序列是一个 递增的有序序列
- 同一数据集的二叉查找树 不唯一,但是中序序列唯一
2. 二叉查找树的操作
- 查找:在树中查找关键字
keykey == node.val查找成功key < node.val,则递归地在node的左子树查找keykey > node.val,则递归地在node的右子树查找key
- 插入:若二叉排序树为空树,则新插入的结点为根结点;否则,新插入的结点必为一个新的叶结点
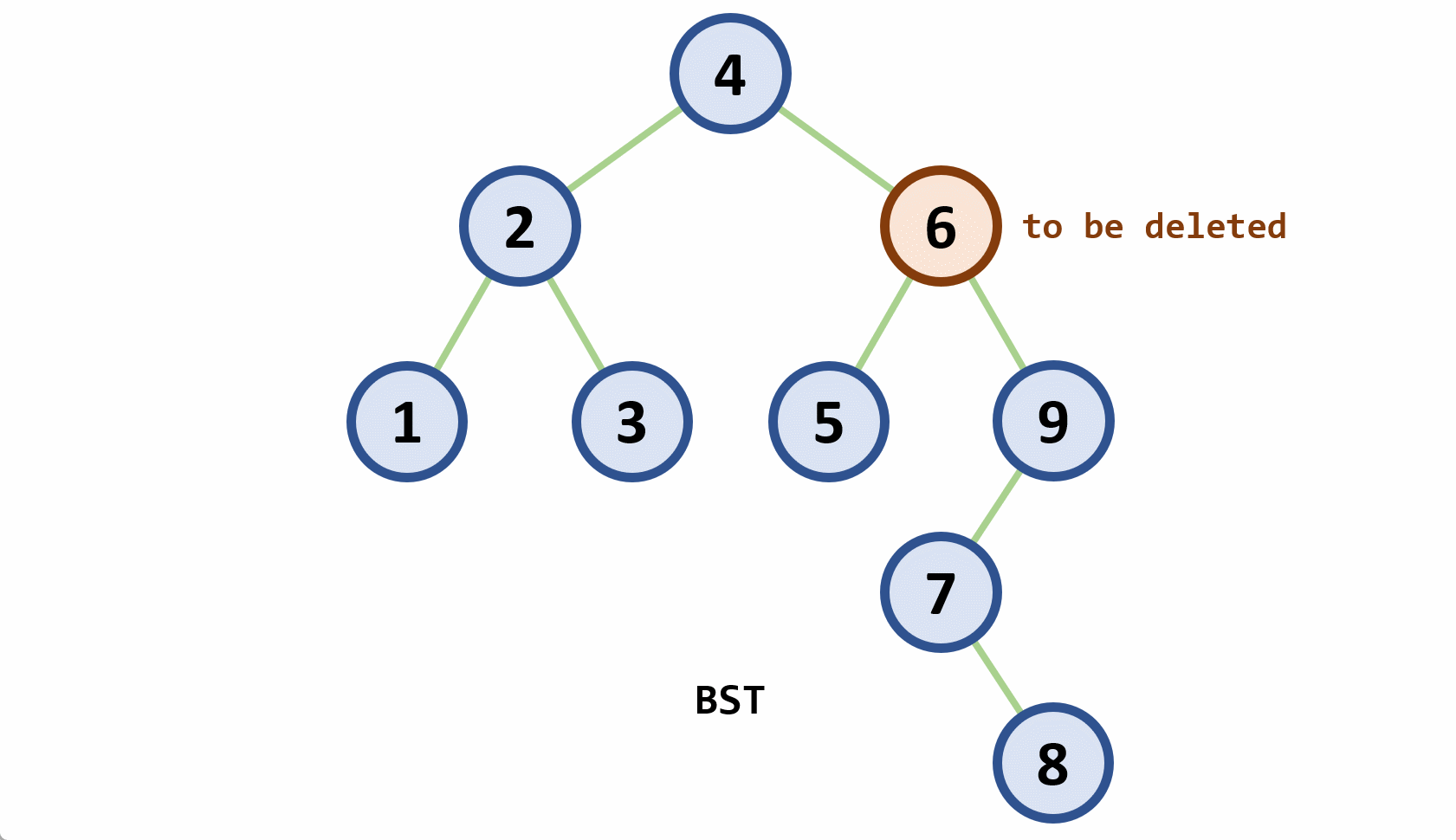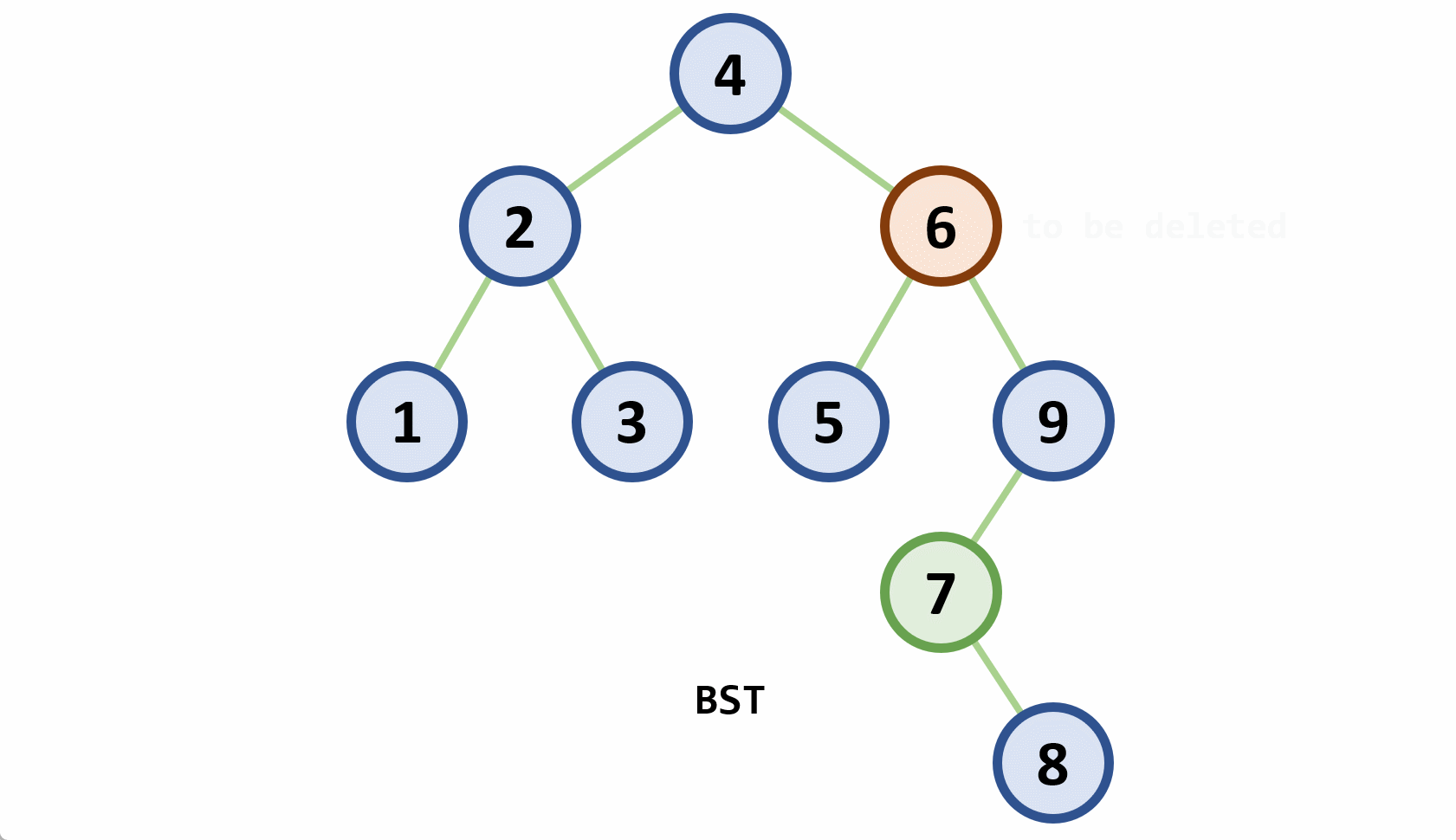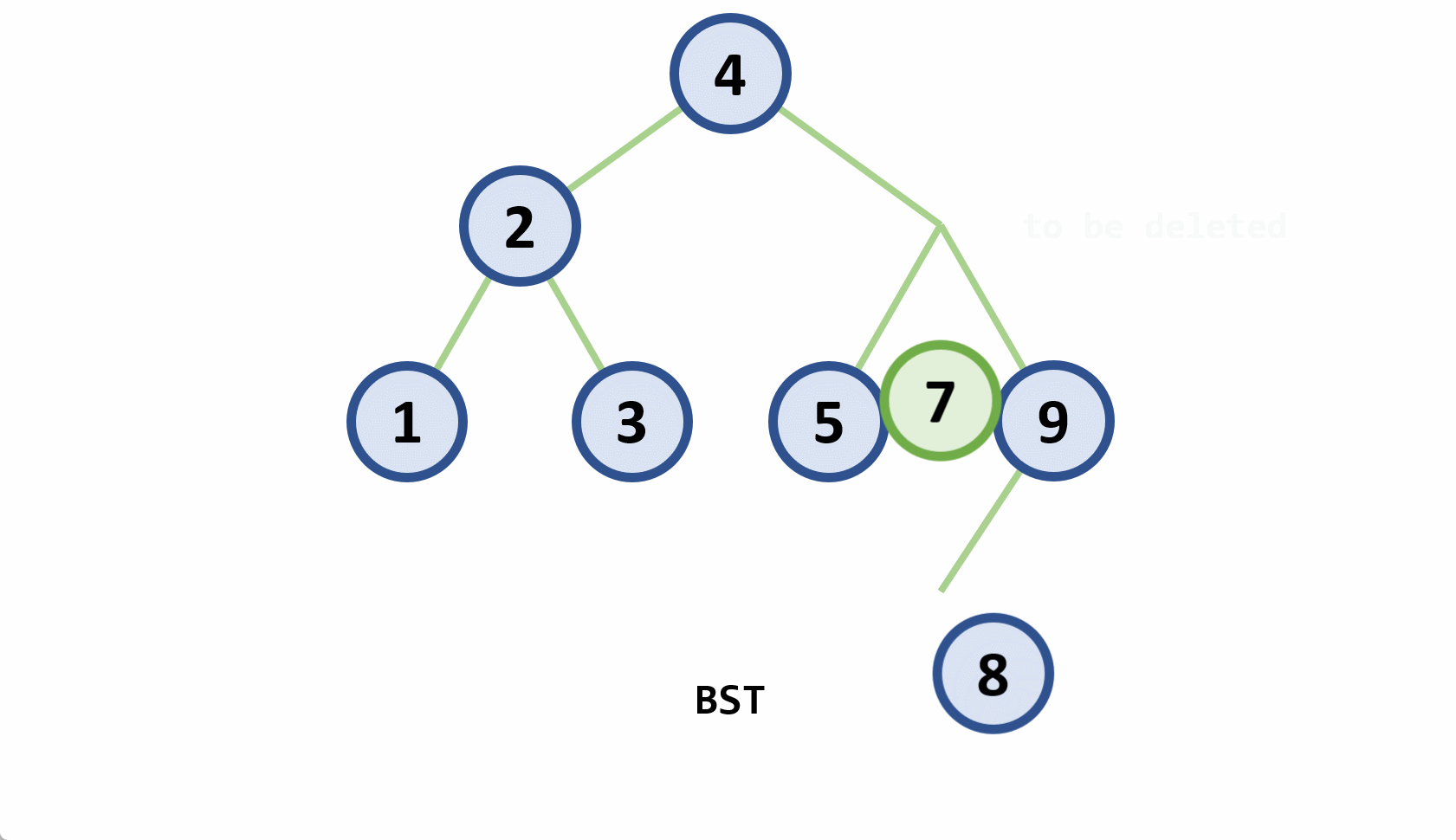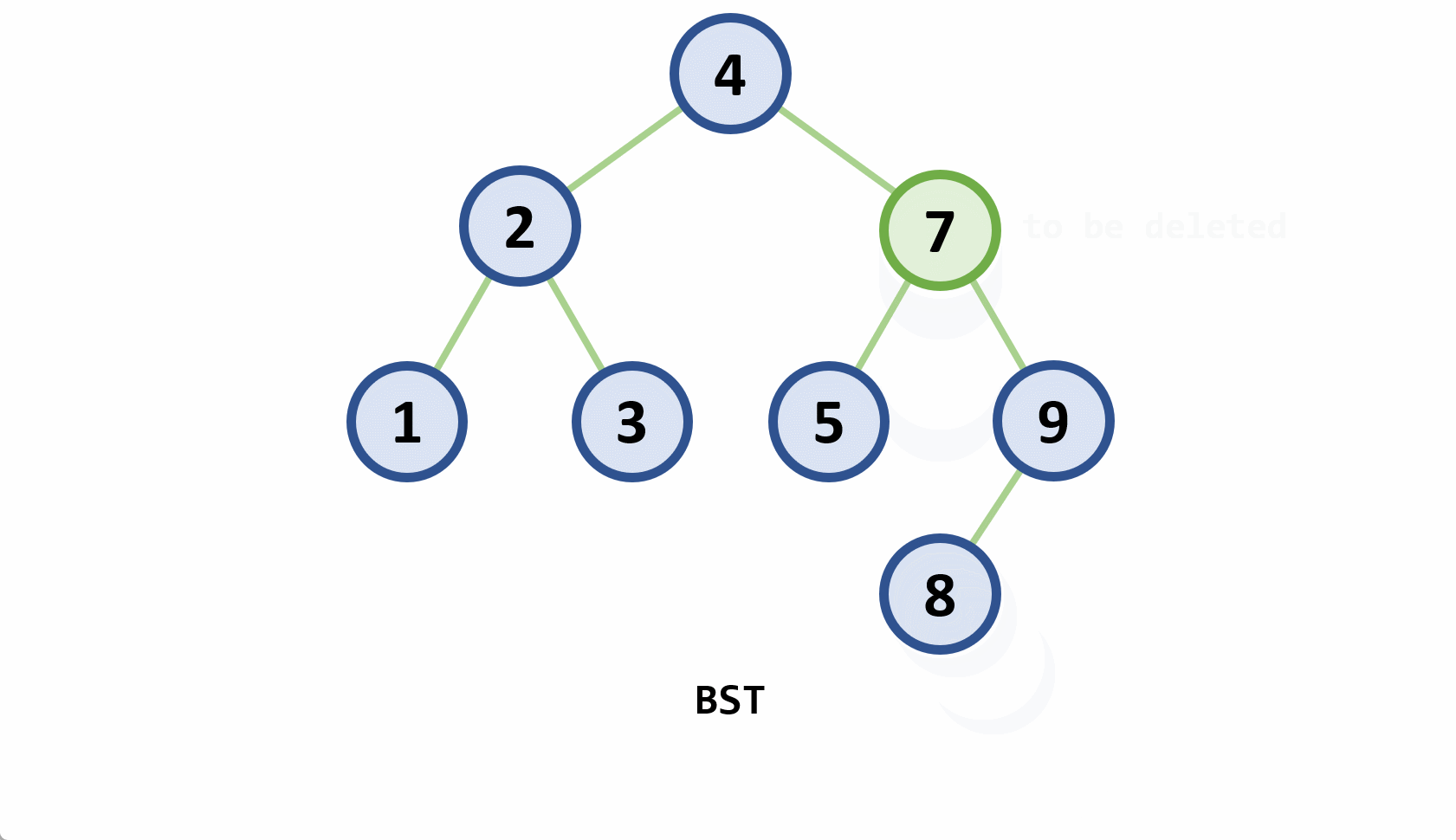
- 删除
3. 平衡二叉查找树
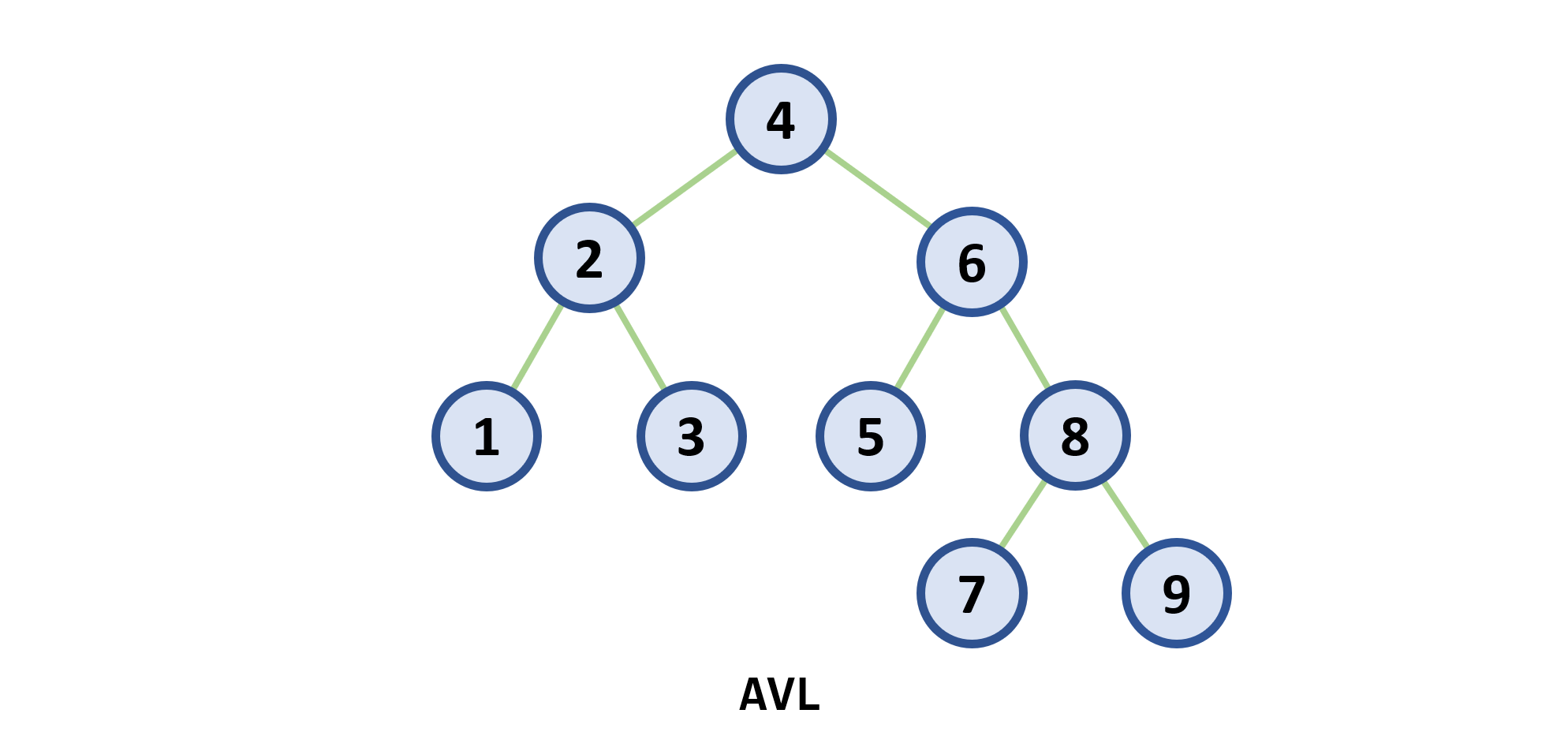
-
平衡二叉查找树:一棵
-
-
结点的平衡因子
- 每个结点附加一个数字,给出该结点右子树的高度减去左子树的高度所得的高度差。这个数字即为结点的平衡因子
balance - 根据
- 如果一个结点的平衡因子的绝对值大于1,则这棵二叉查找树就失去了平衡,不再是
- 如果一棵二叉查找树是高度平衡的,它就成为
- 每个结点附加一个数字,给出该结点右子树的高度减去左子树的高度所得的高度差。这个数字即为结点的平衡因子
-
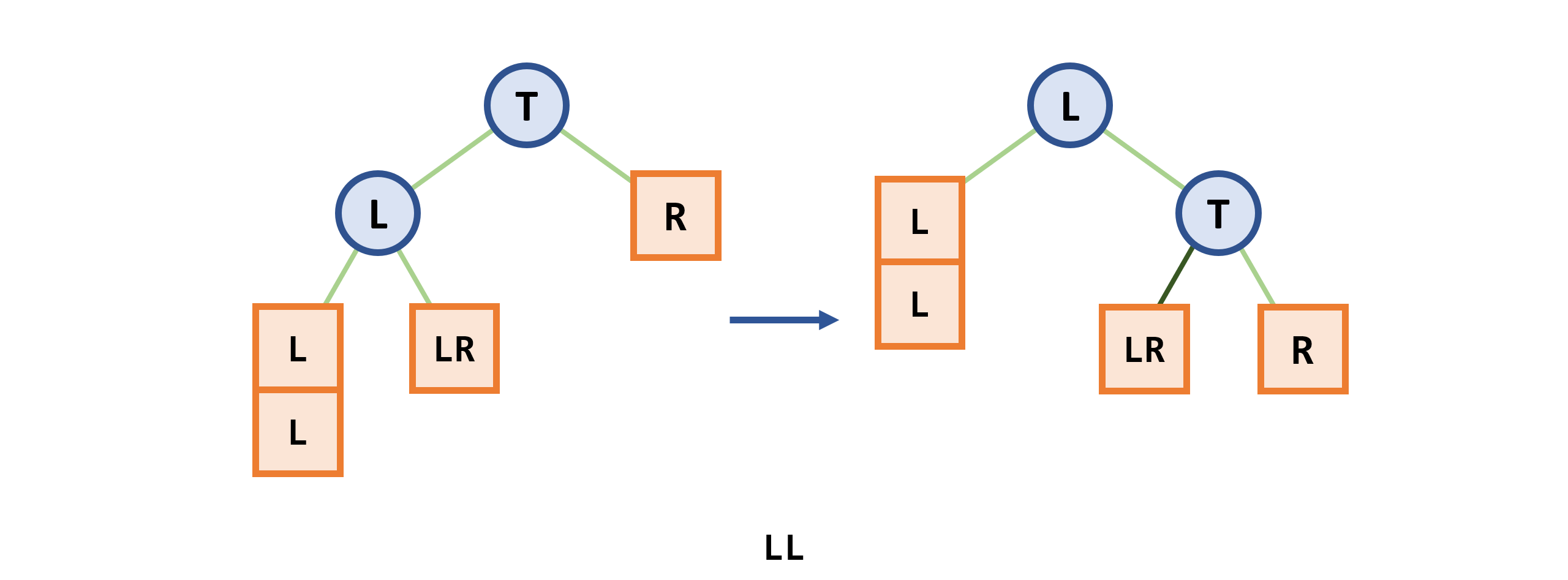
- 在向一棵本来是高度平衡的AVL树中插入一个新结点时,如果树中某个结点的平衡因子的绝对值
|balance|> 1,则出现了不平衡,需要做平衡化处理 - 算法从一棵空树开始,通过输入一系列对象的关键字,逐步建立
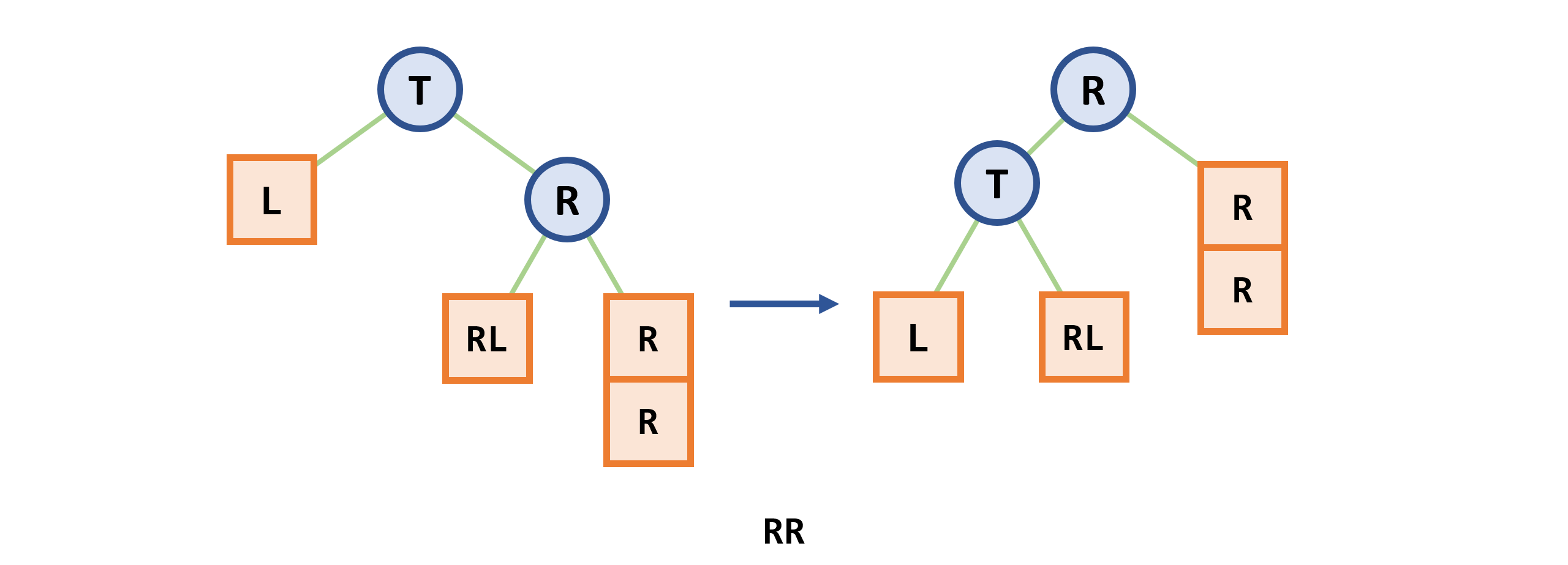
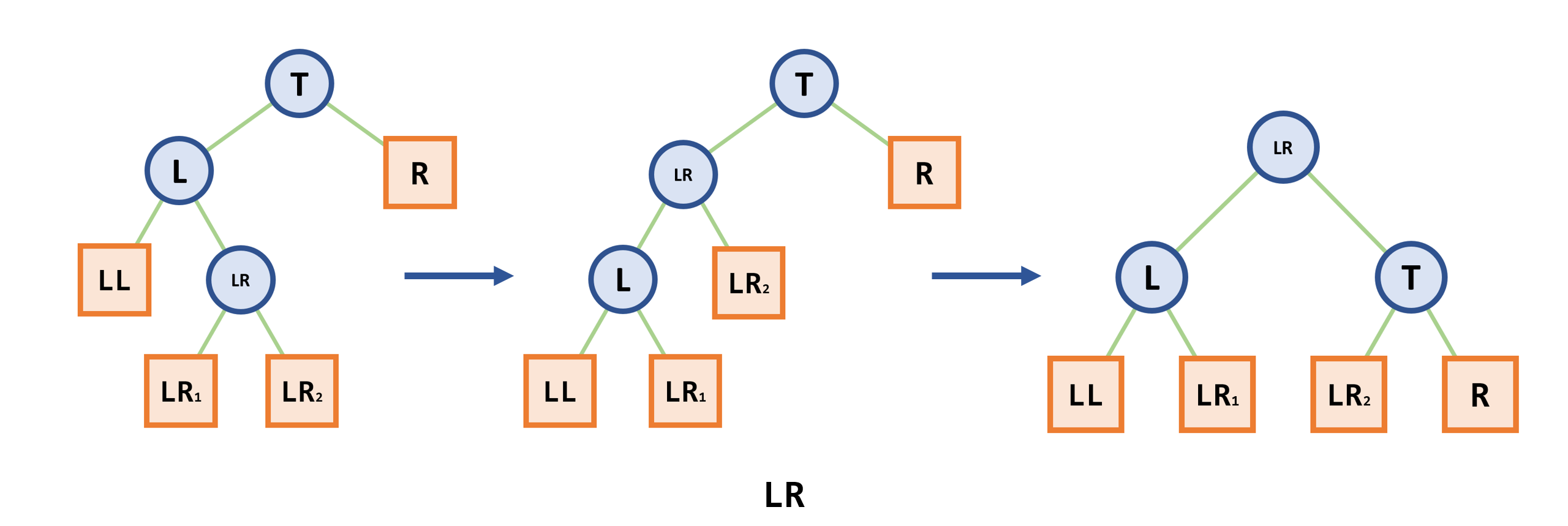
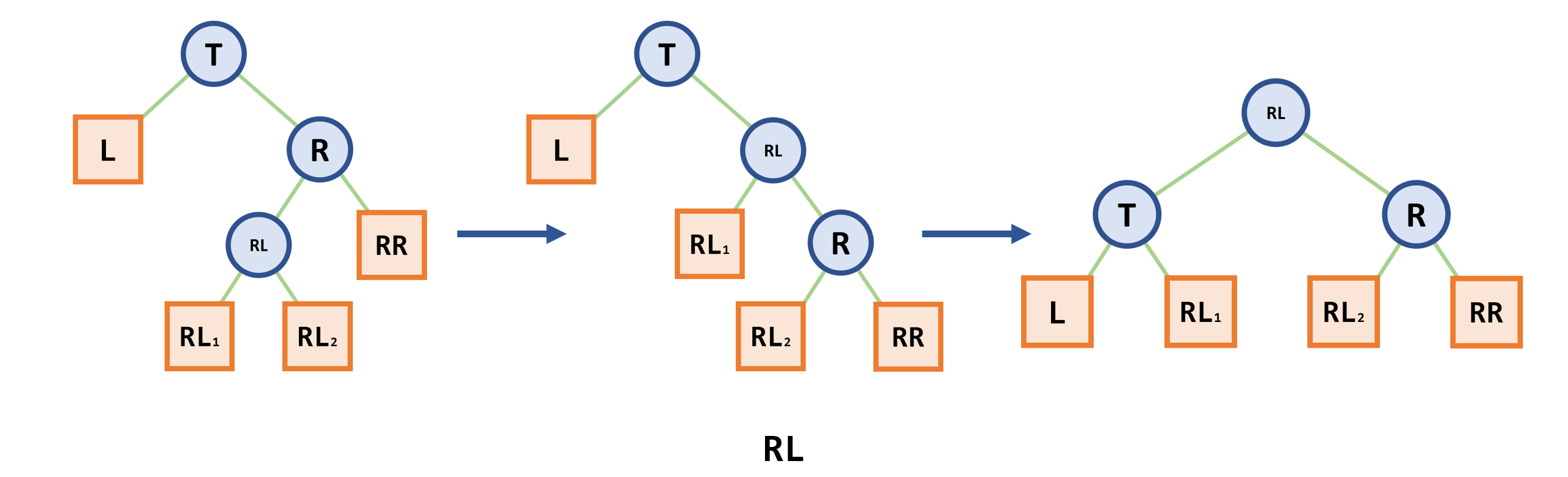
- 平衡旋转
- 在向一棵本来是高度平衡的AVL树中插入一个新结点时,如果树中某个结点的平衡因子的绝对值
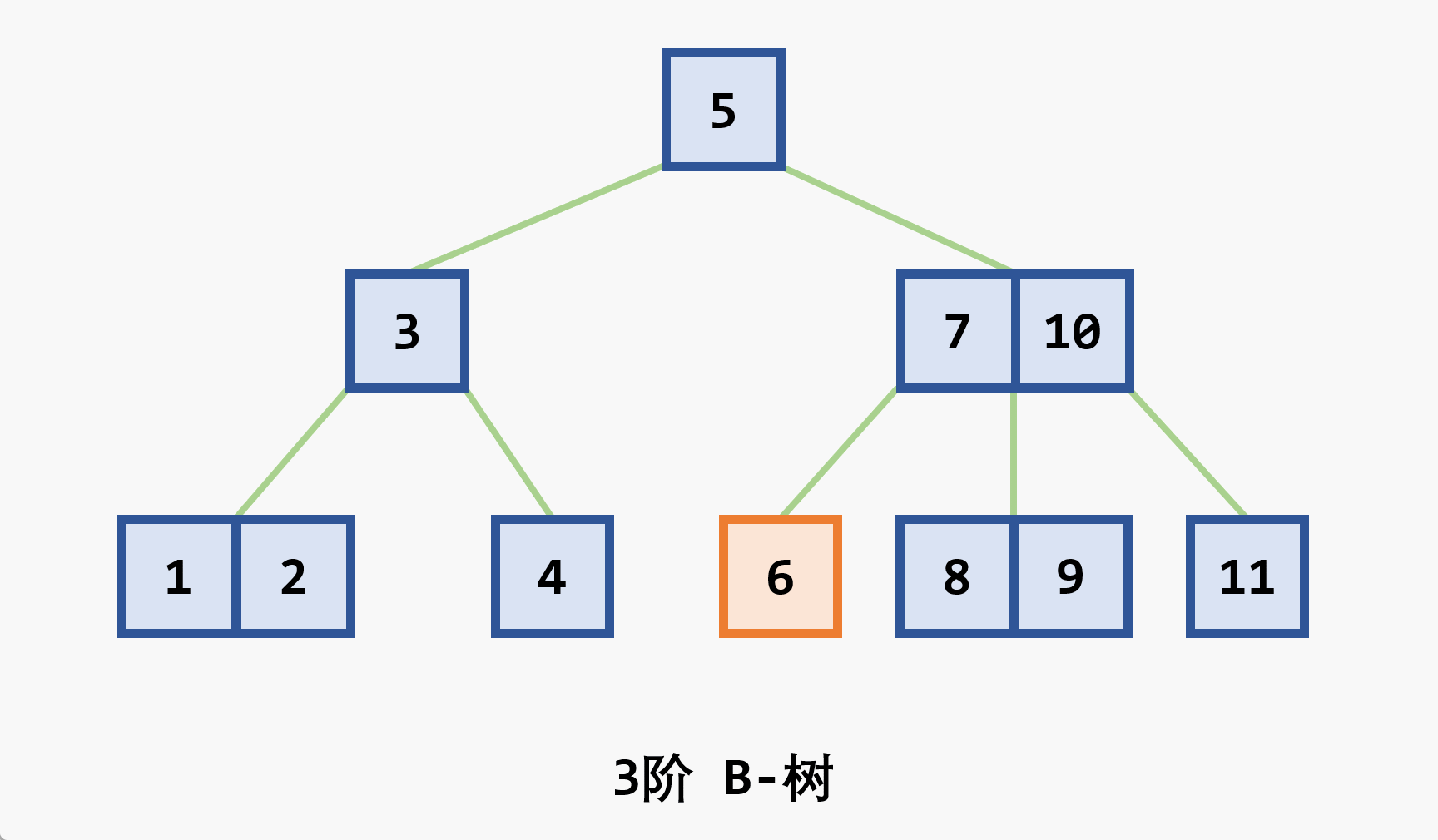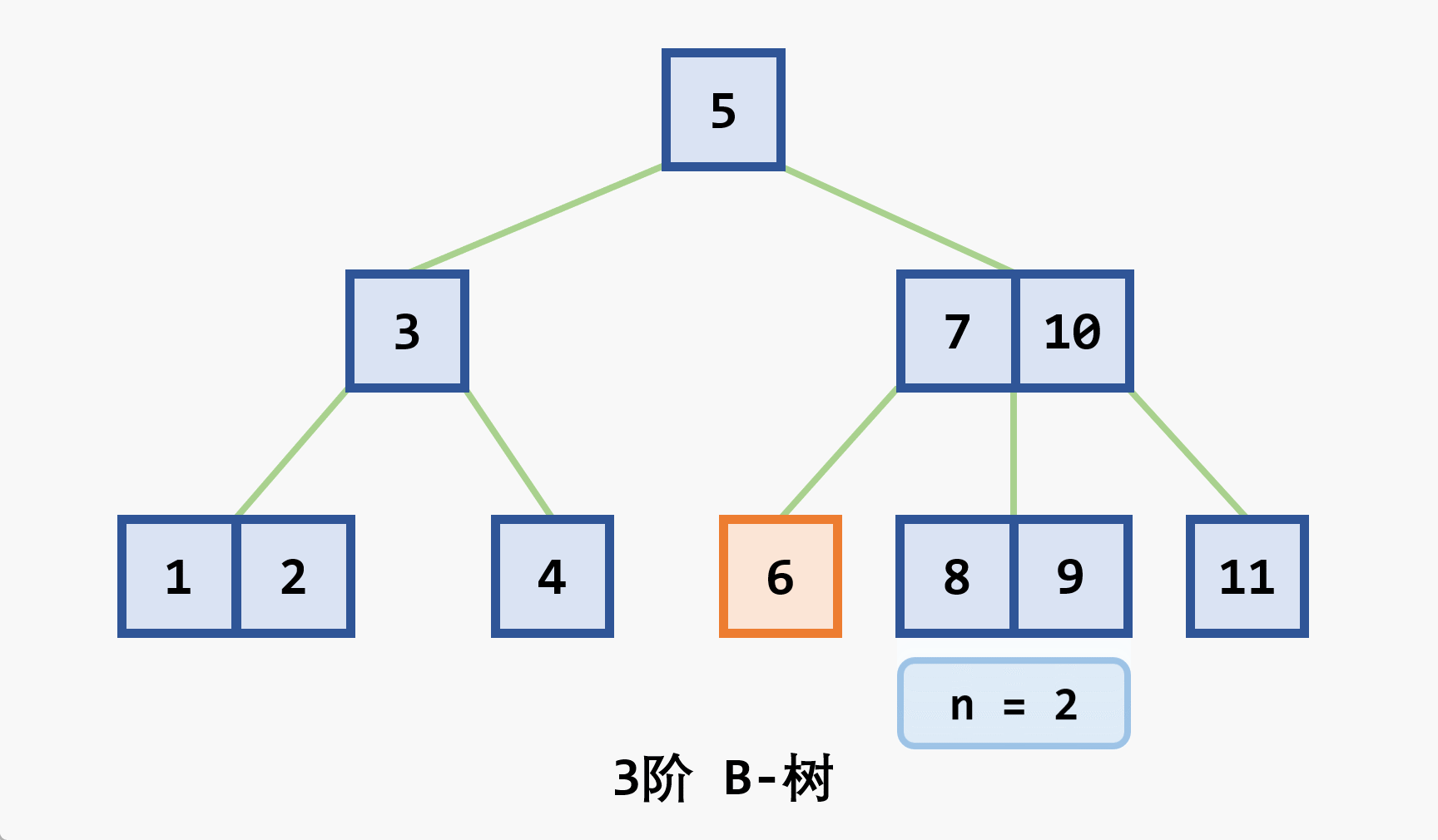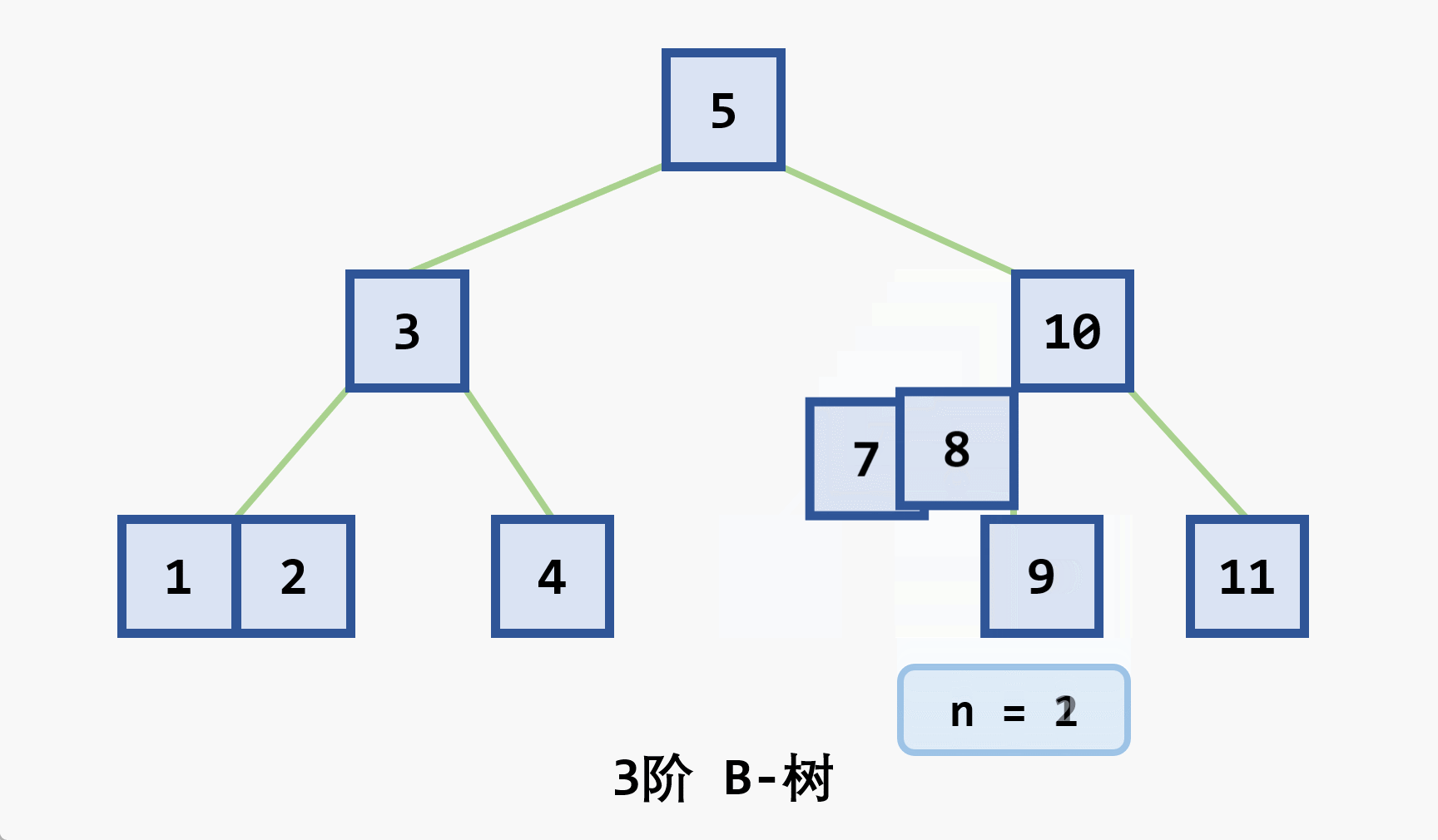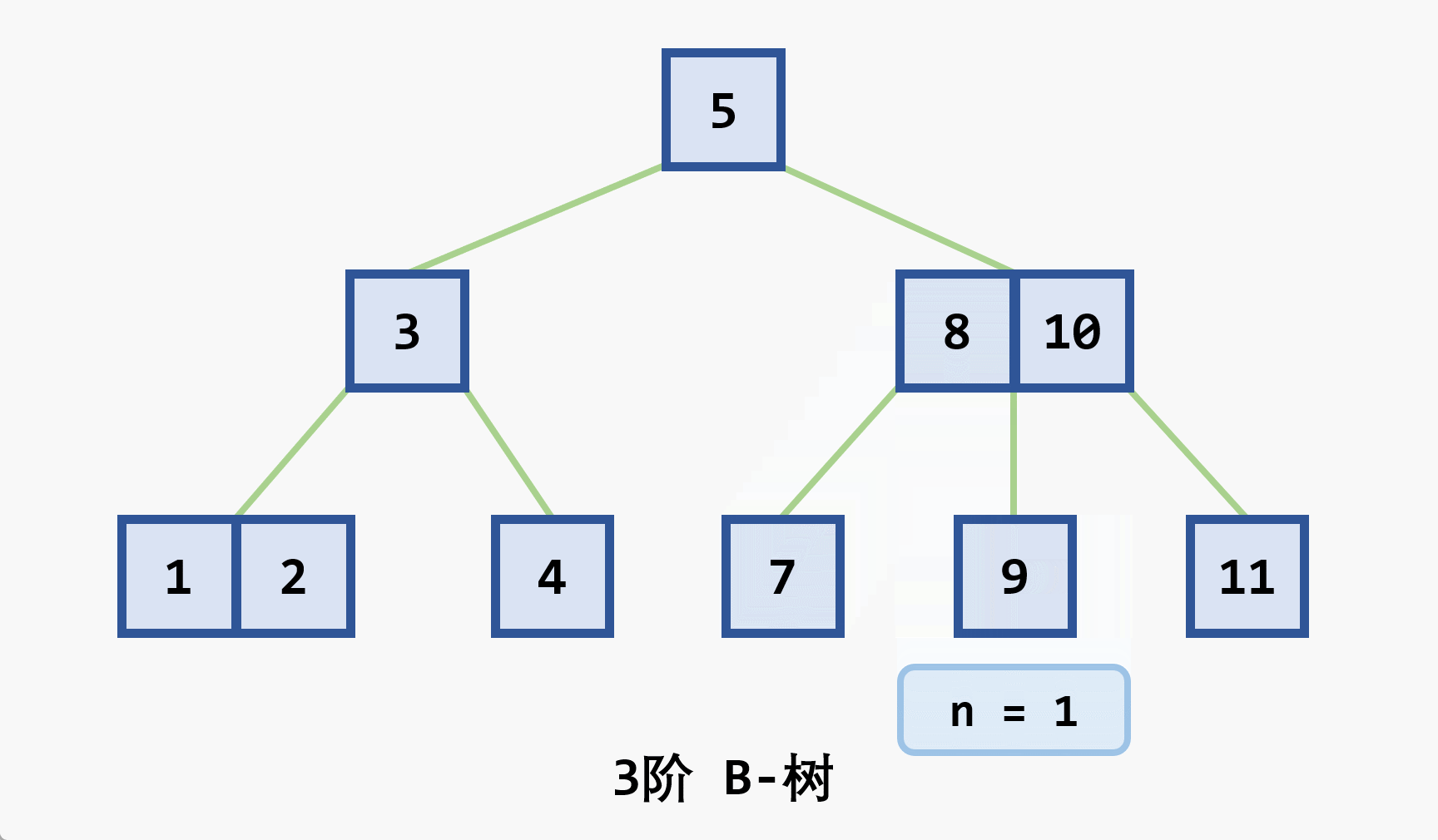
7.
1. 动态查找结构
-
背景:当查找表上的大小超过内存容量的时候,由于必须从磁盘等辅助存储设备中读取这些查找树结构的节点,每次只能根据实际需要读取一个节点,因此,
-
-
- 在
-
-
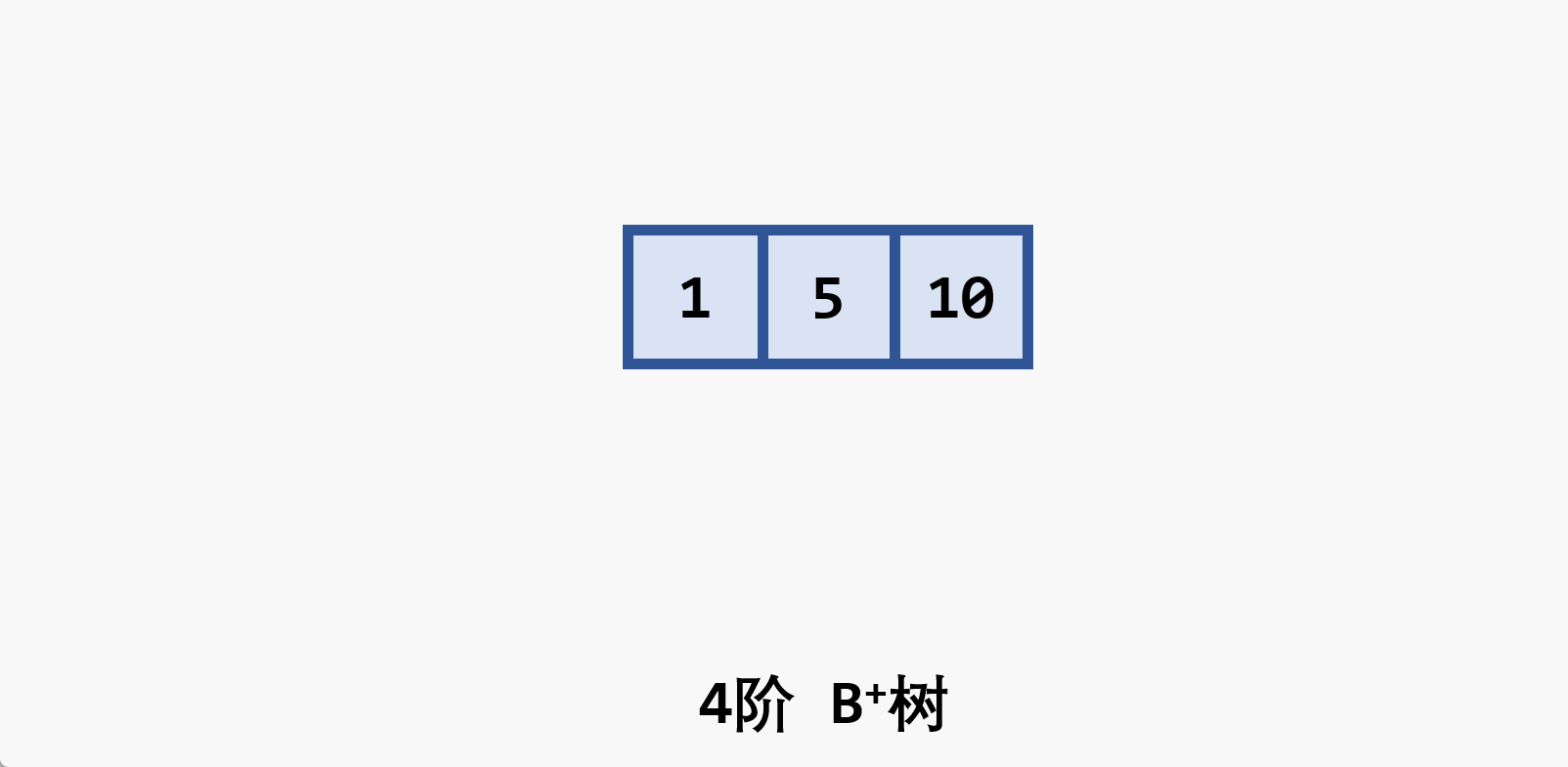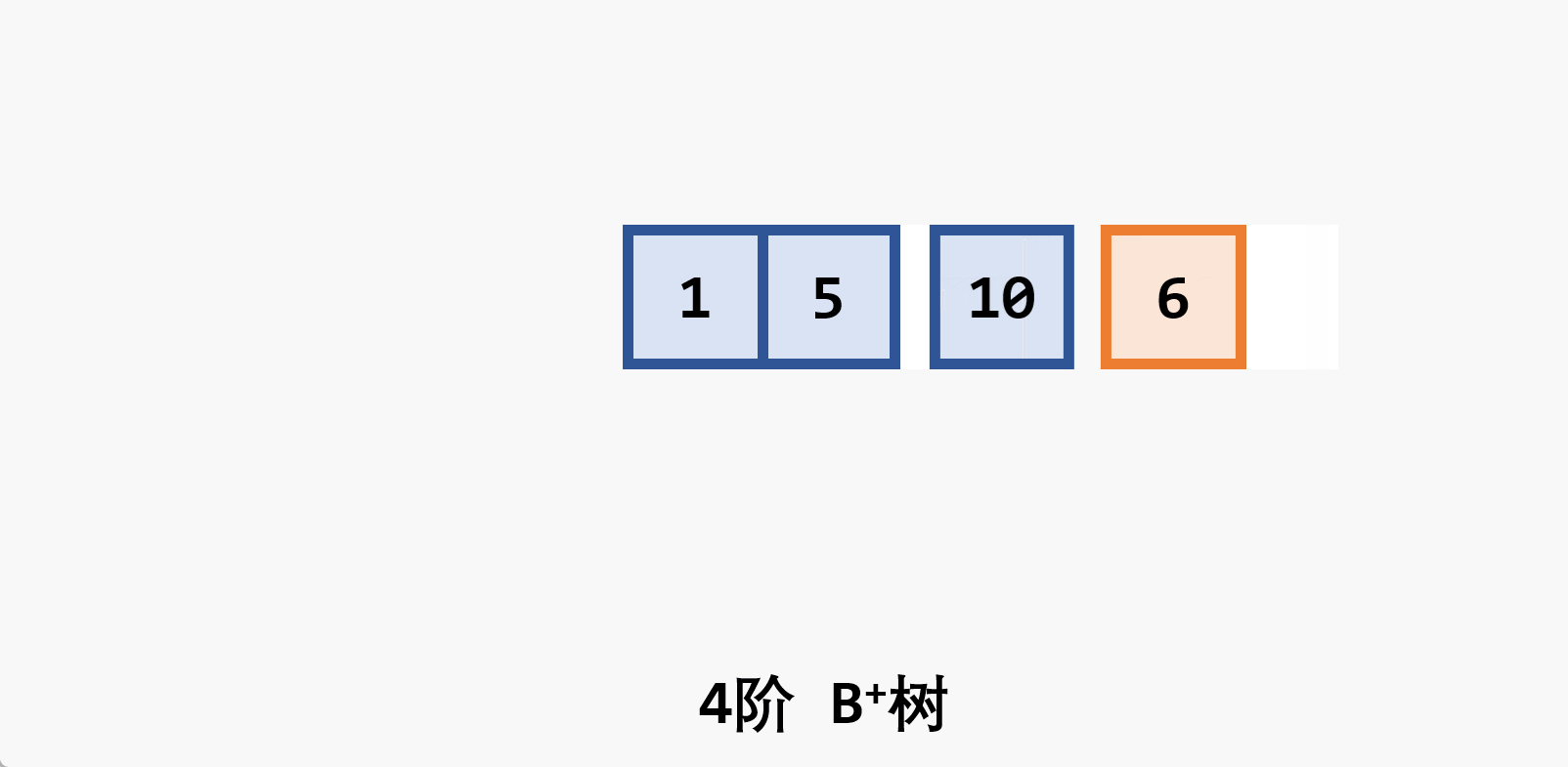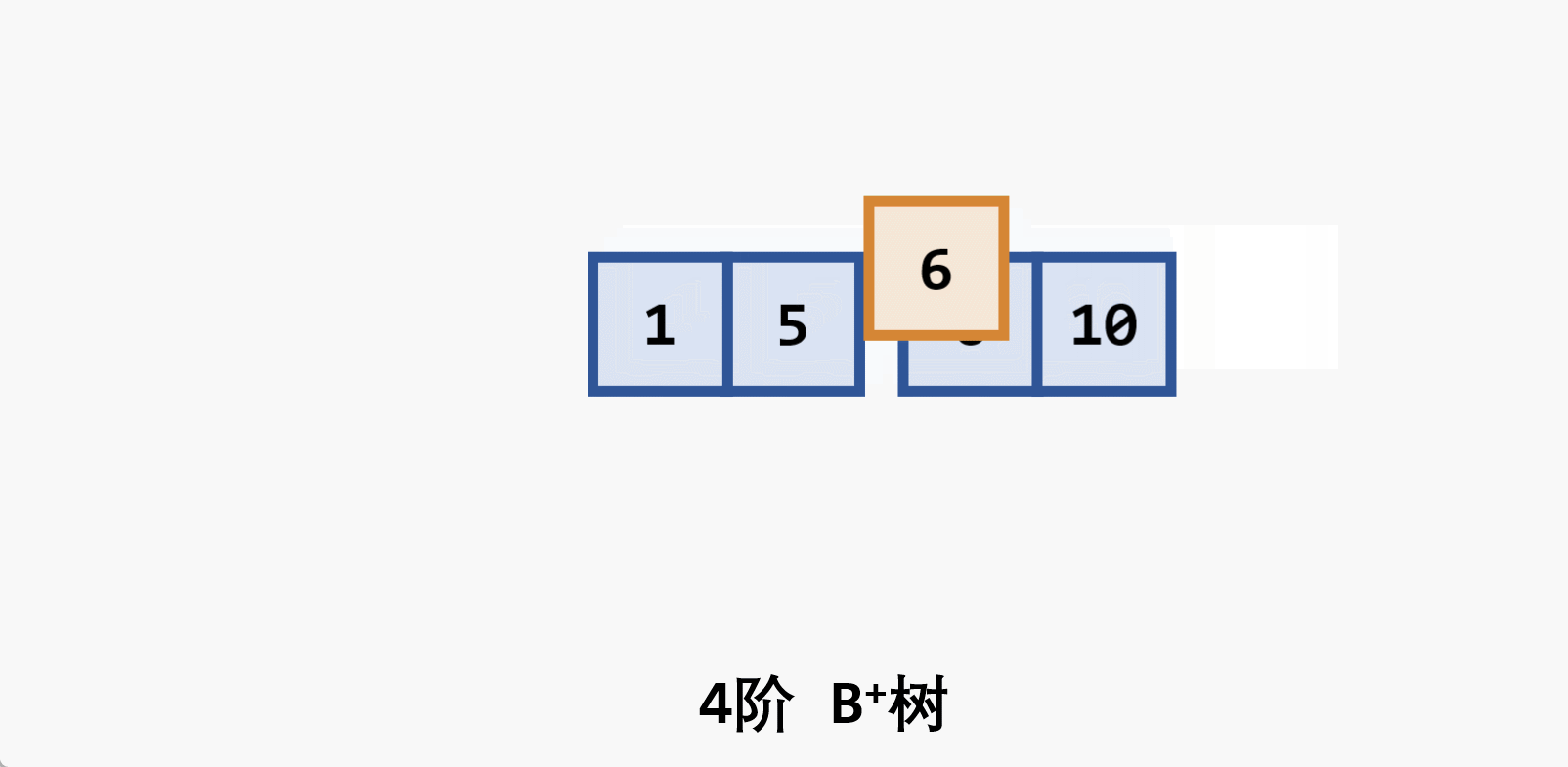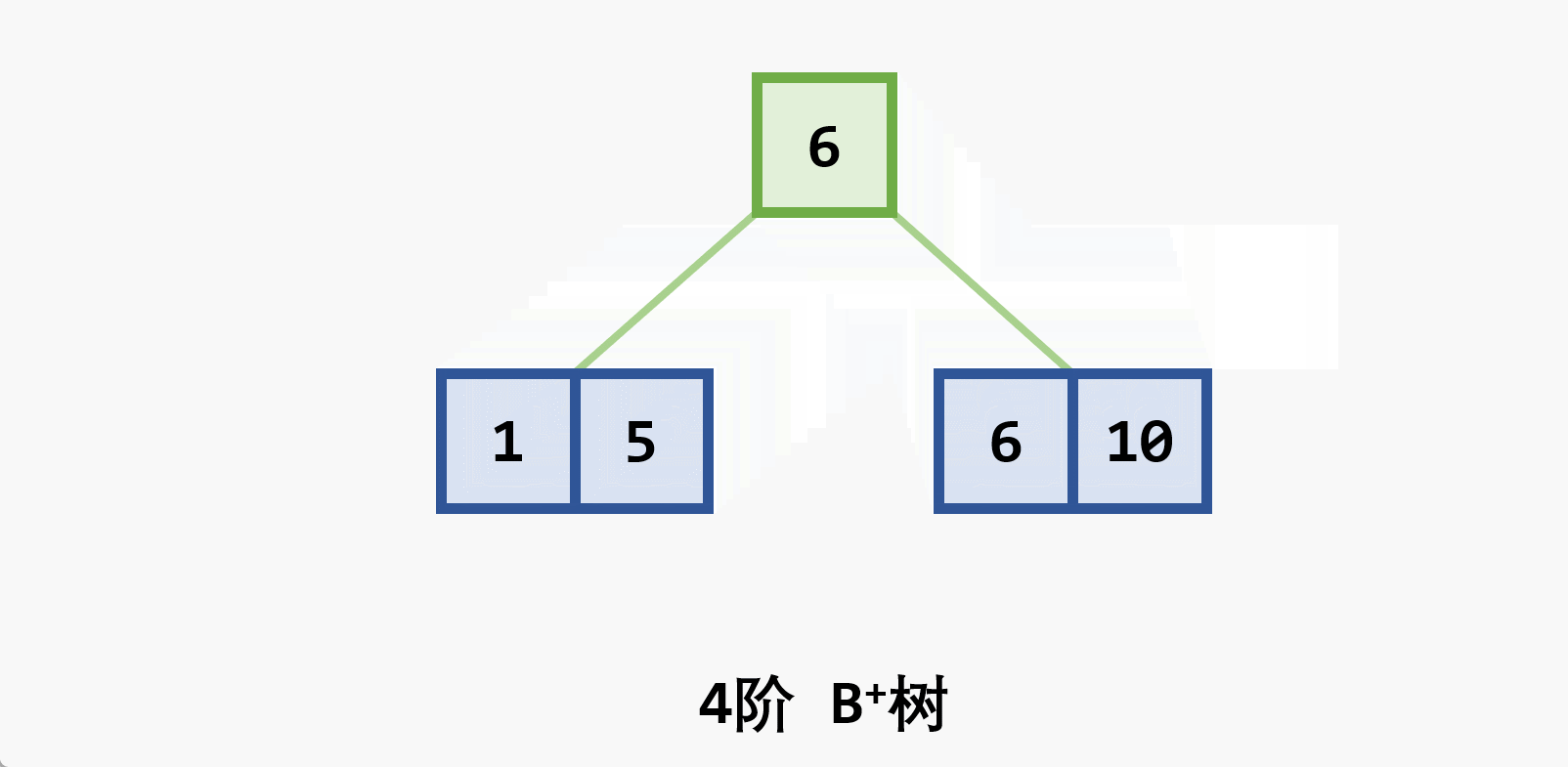
- 基本思想:在
- 若删除结点非最后一层:且被删关键字为
- 若在最后一层上的删除(橙色为待删除结点)
- 基本思想:在
2.
-
背景:
-
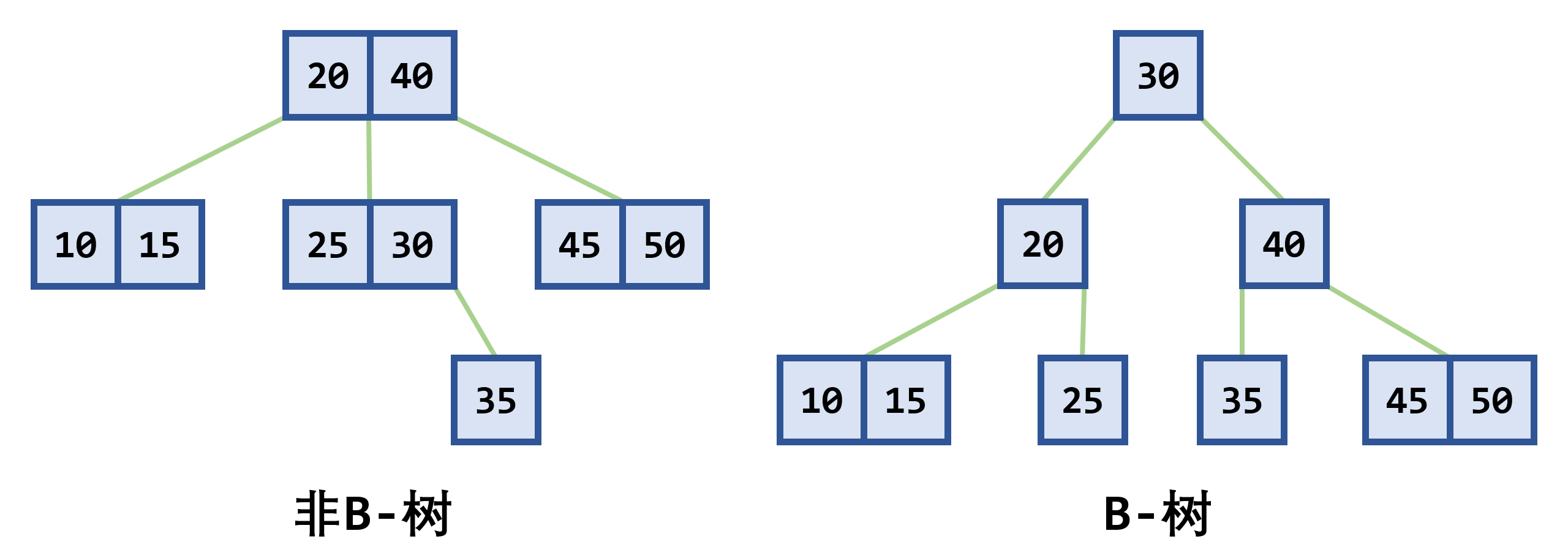
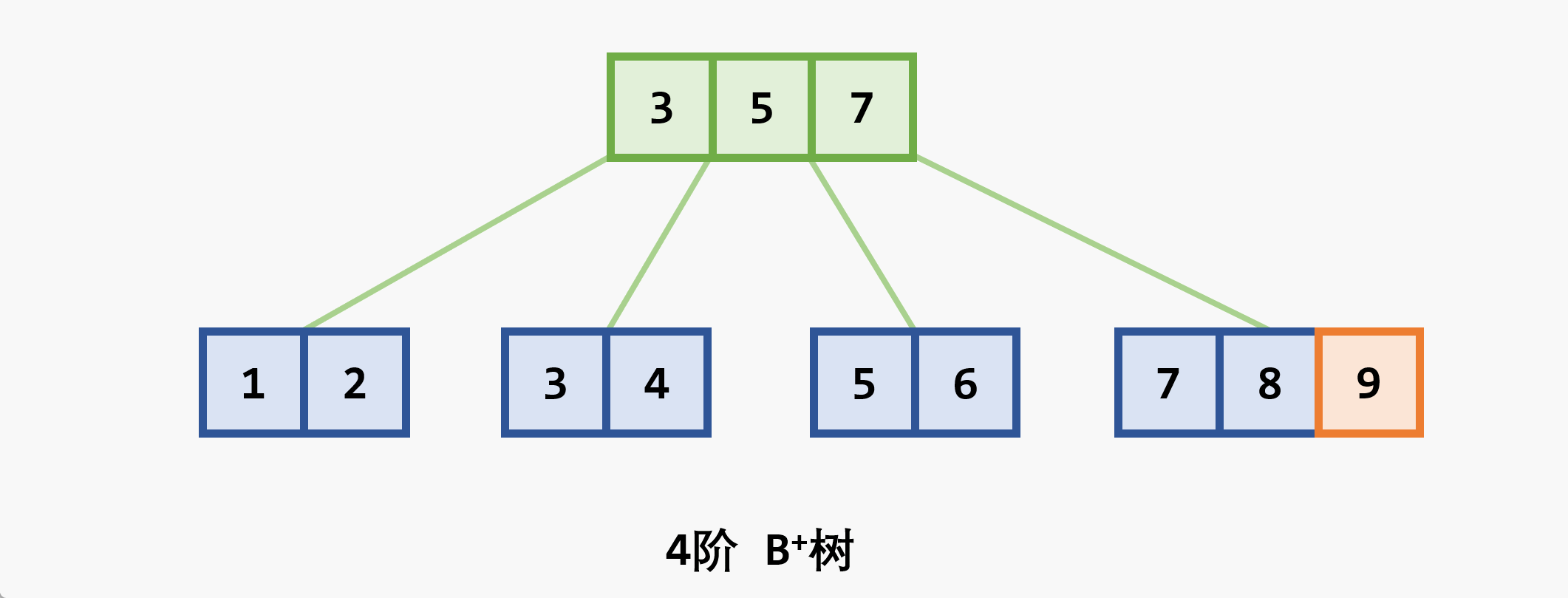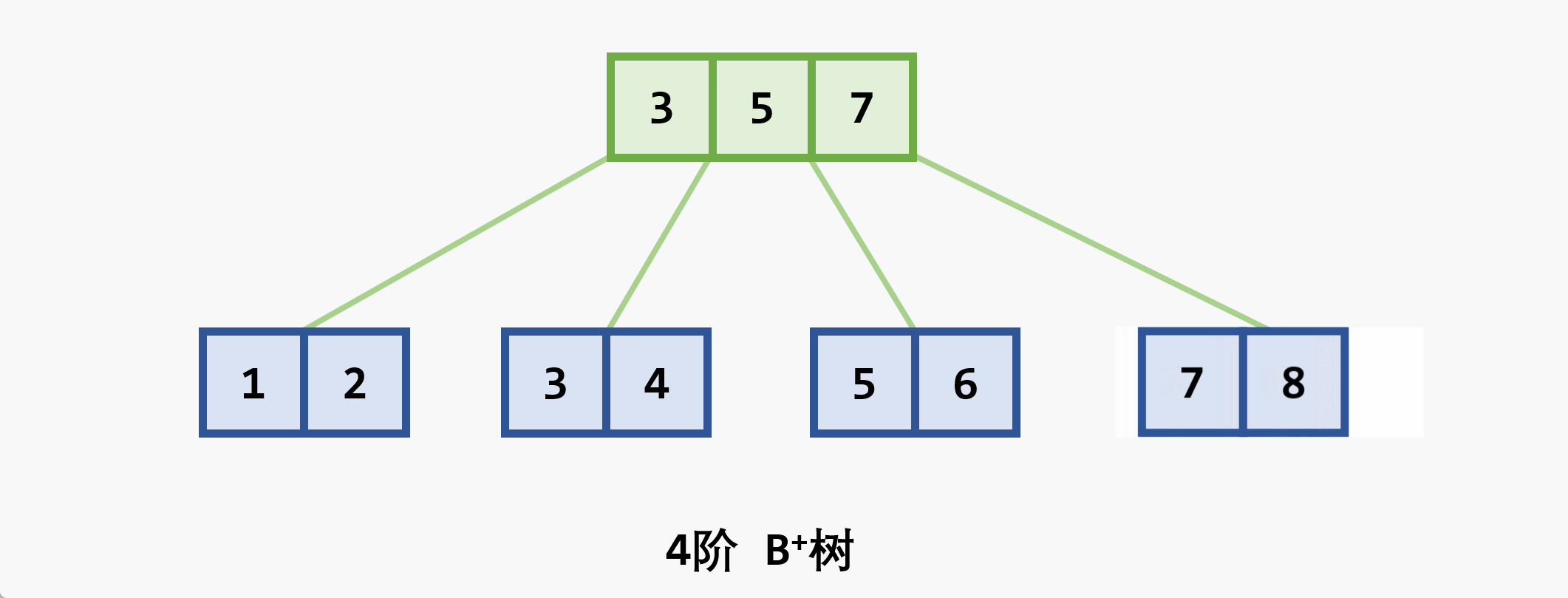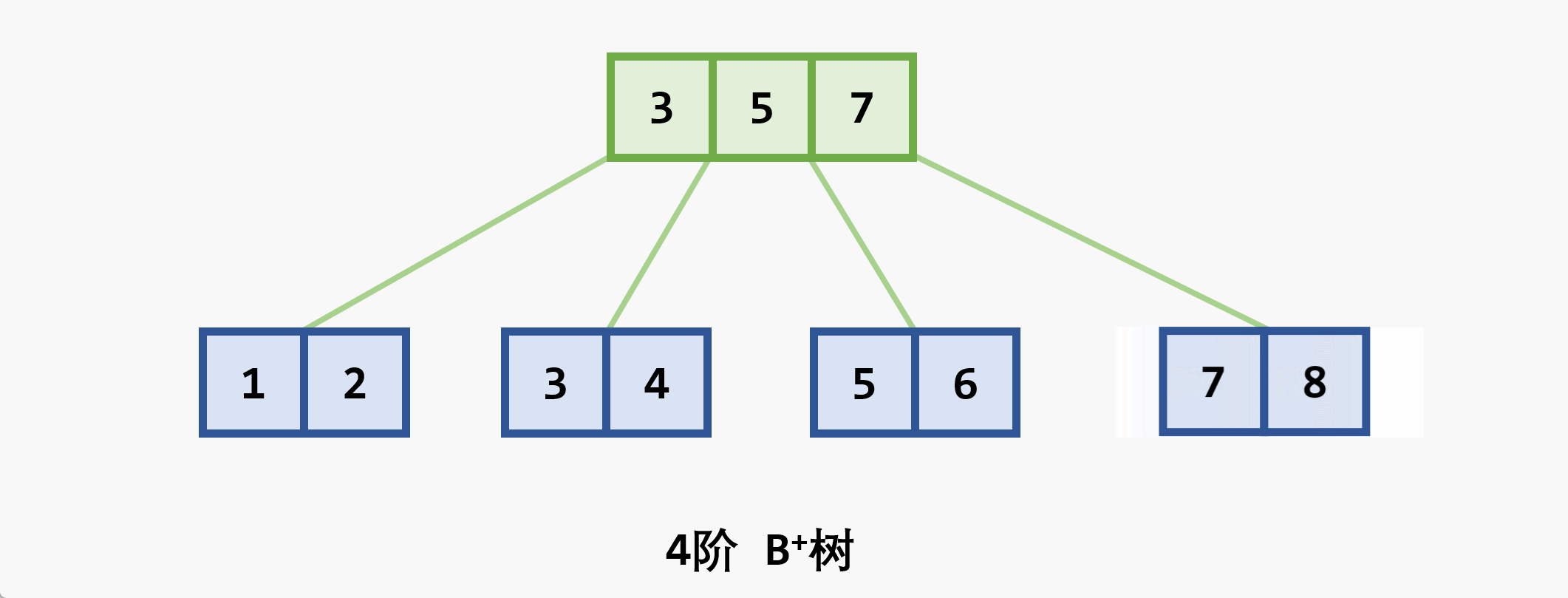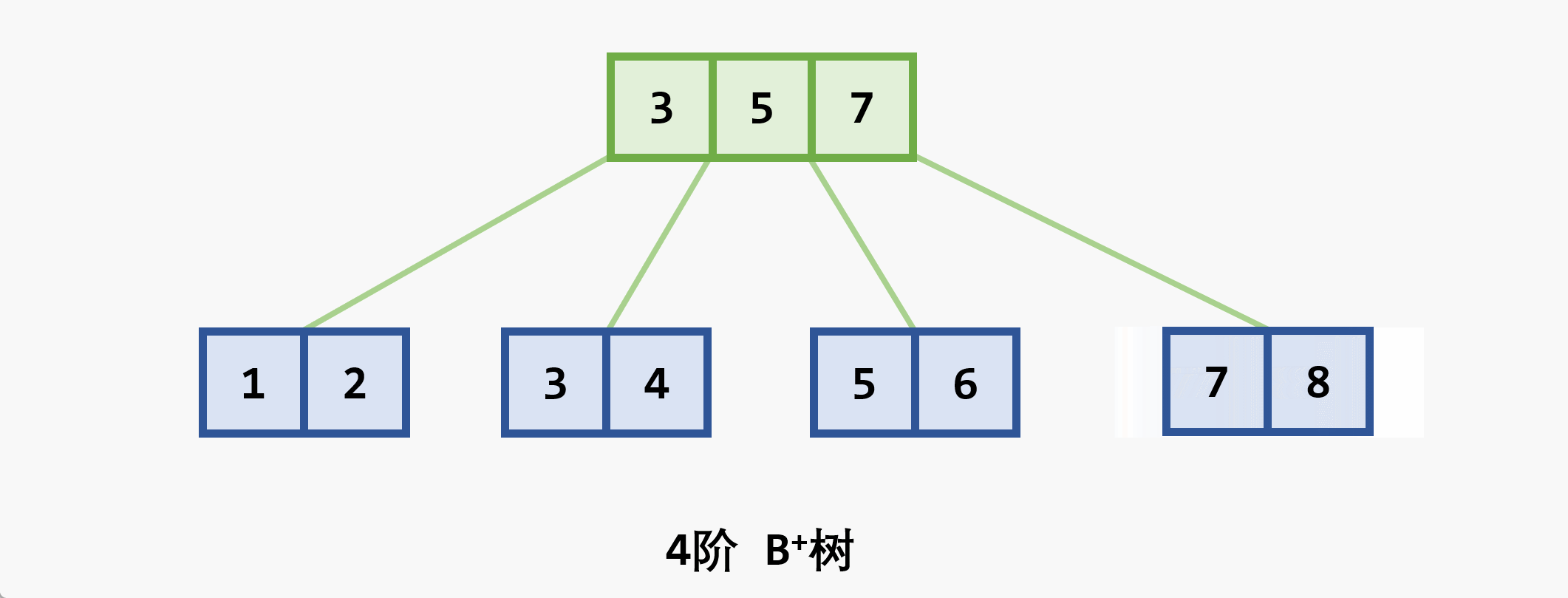
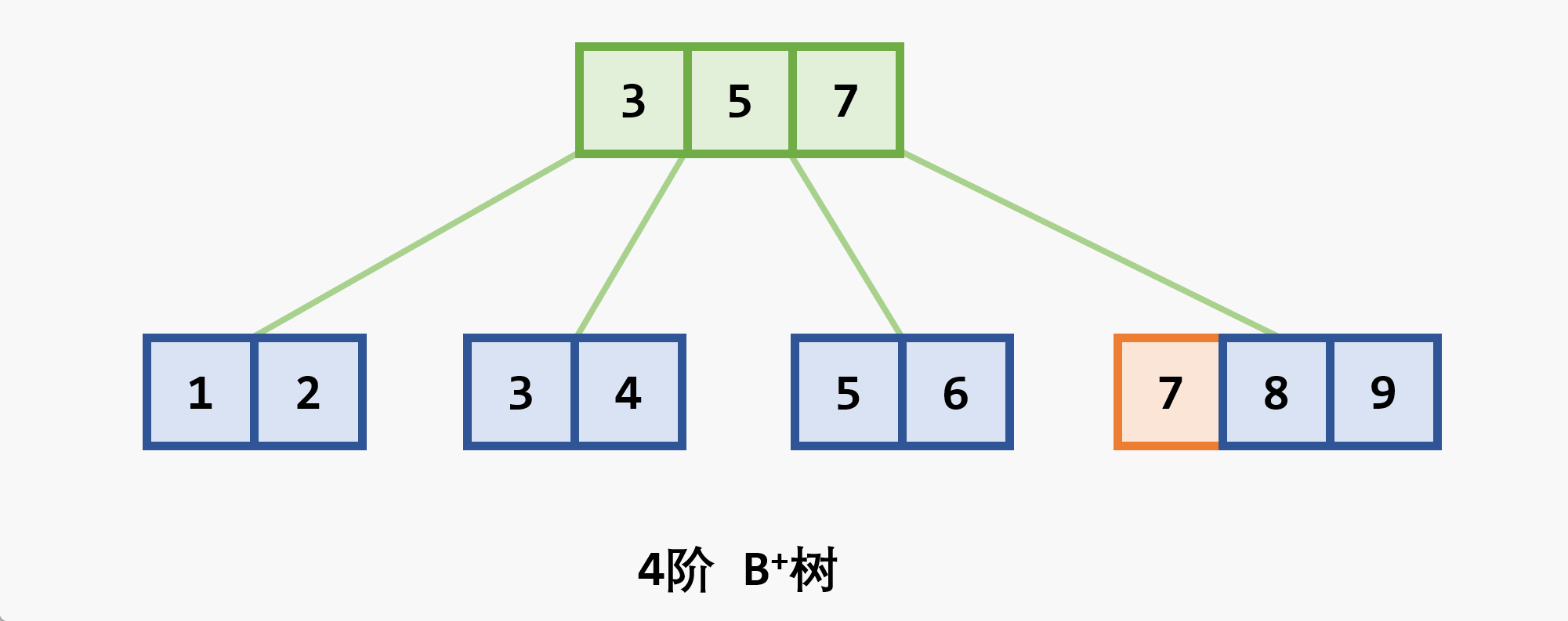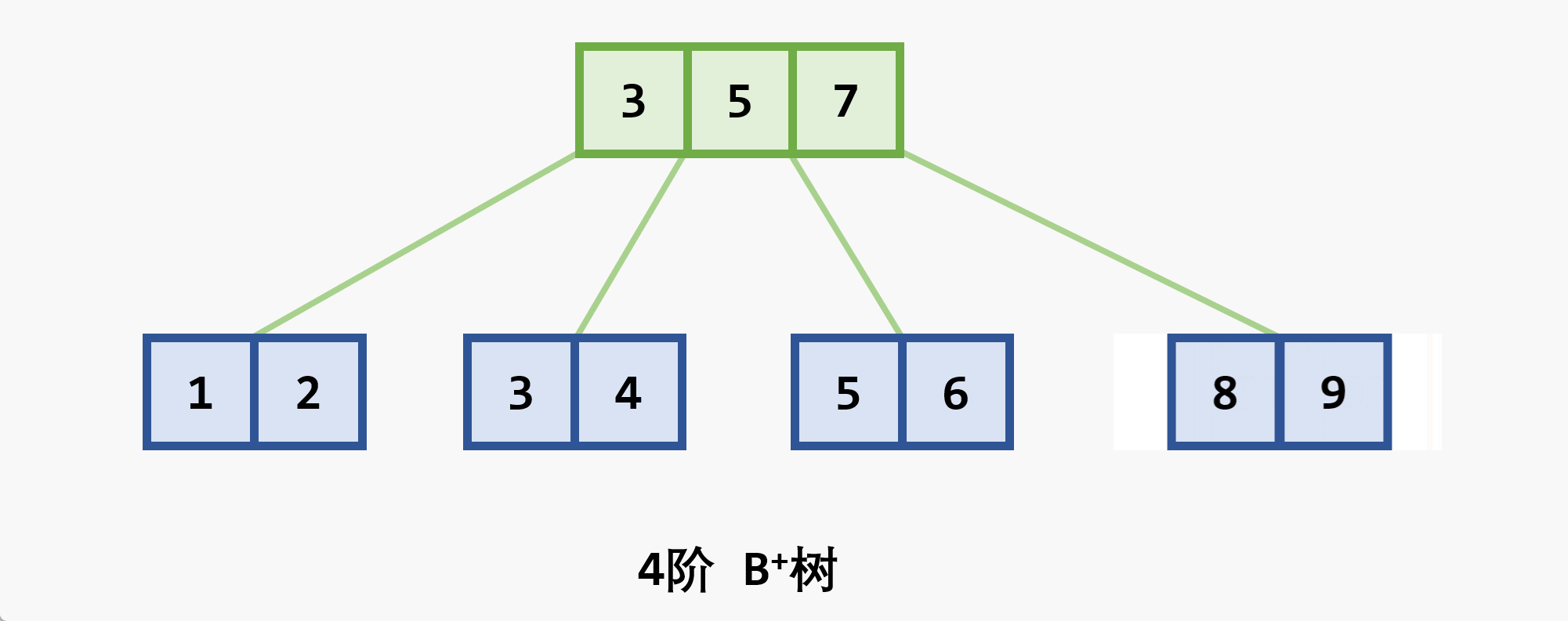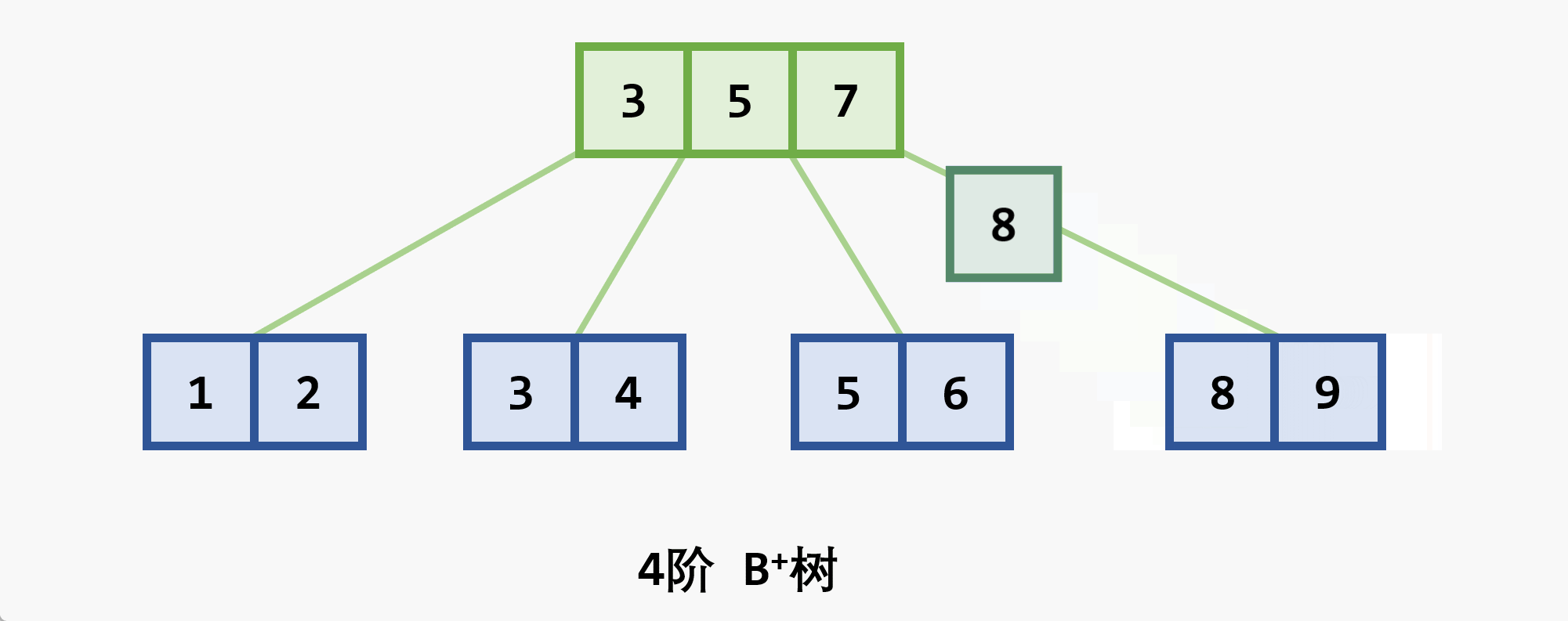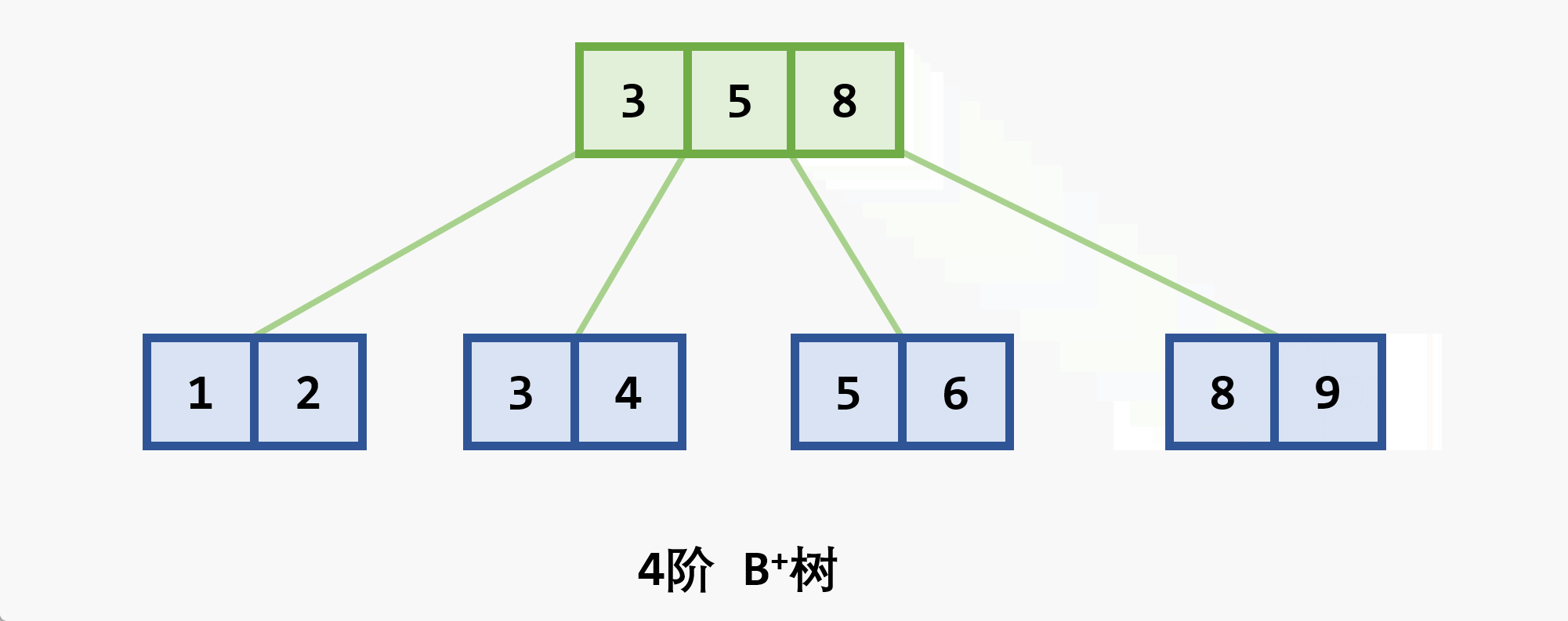
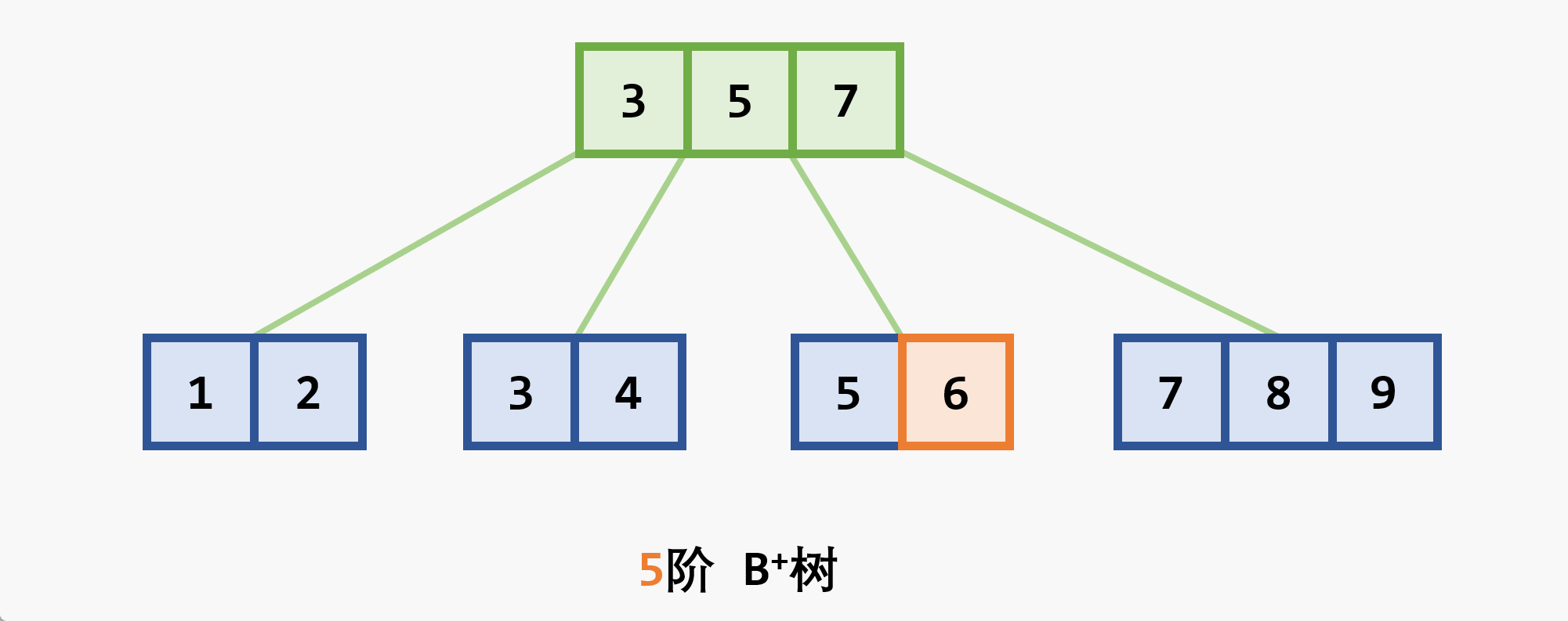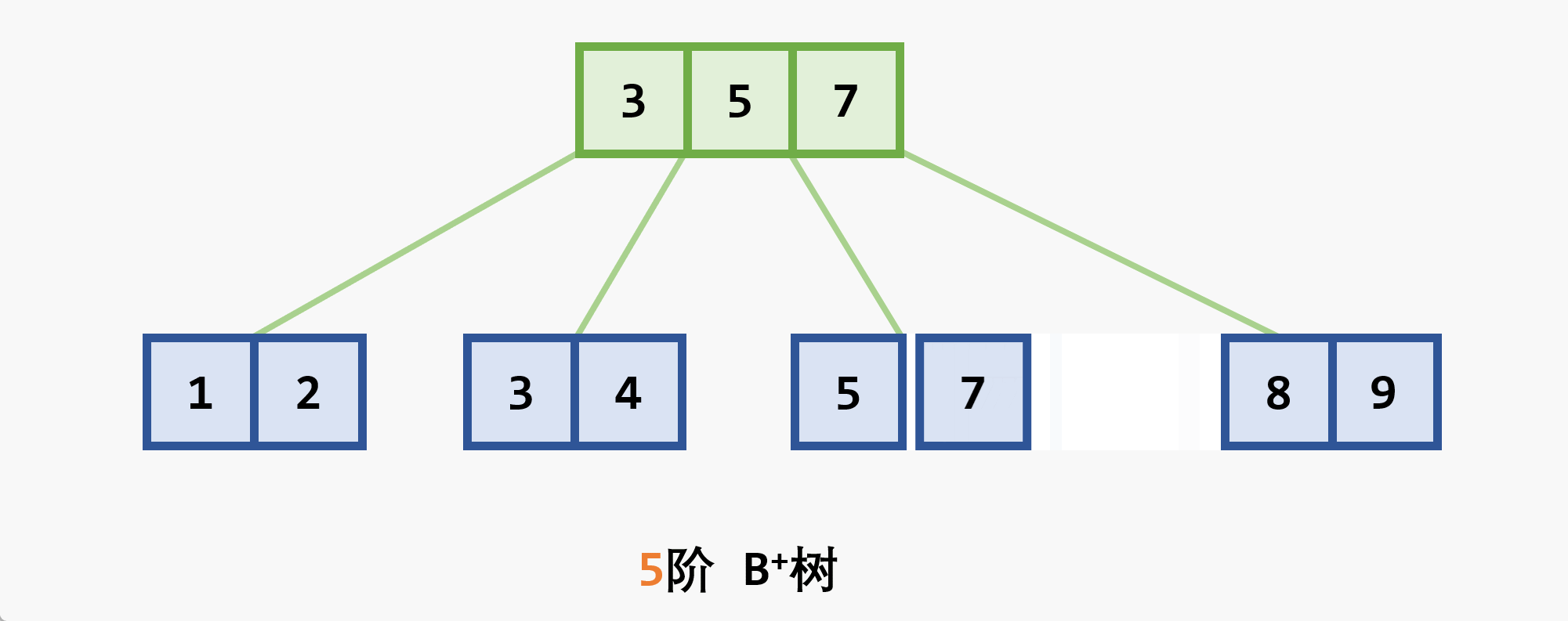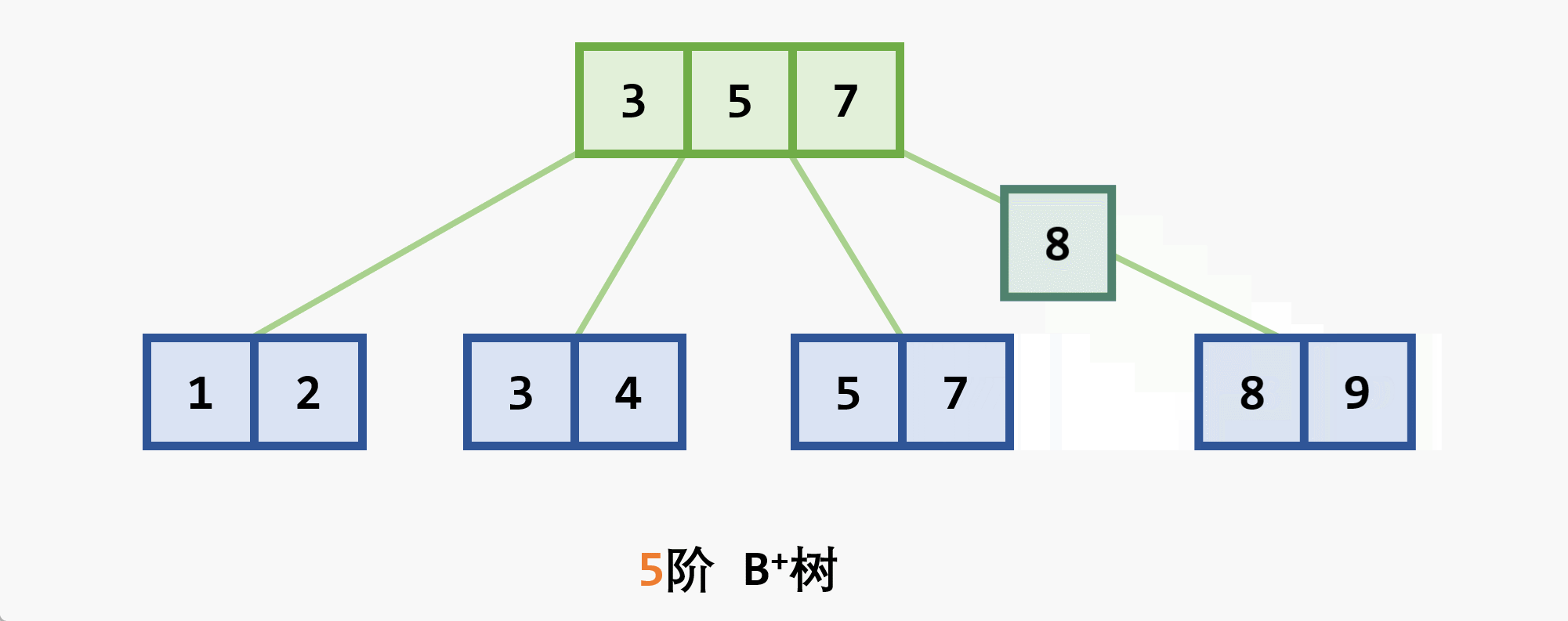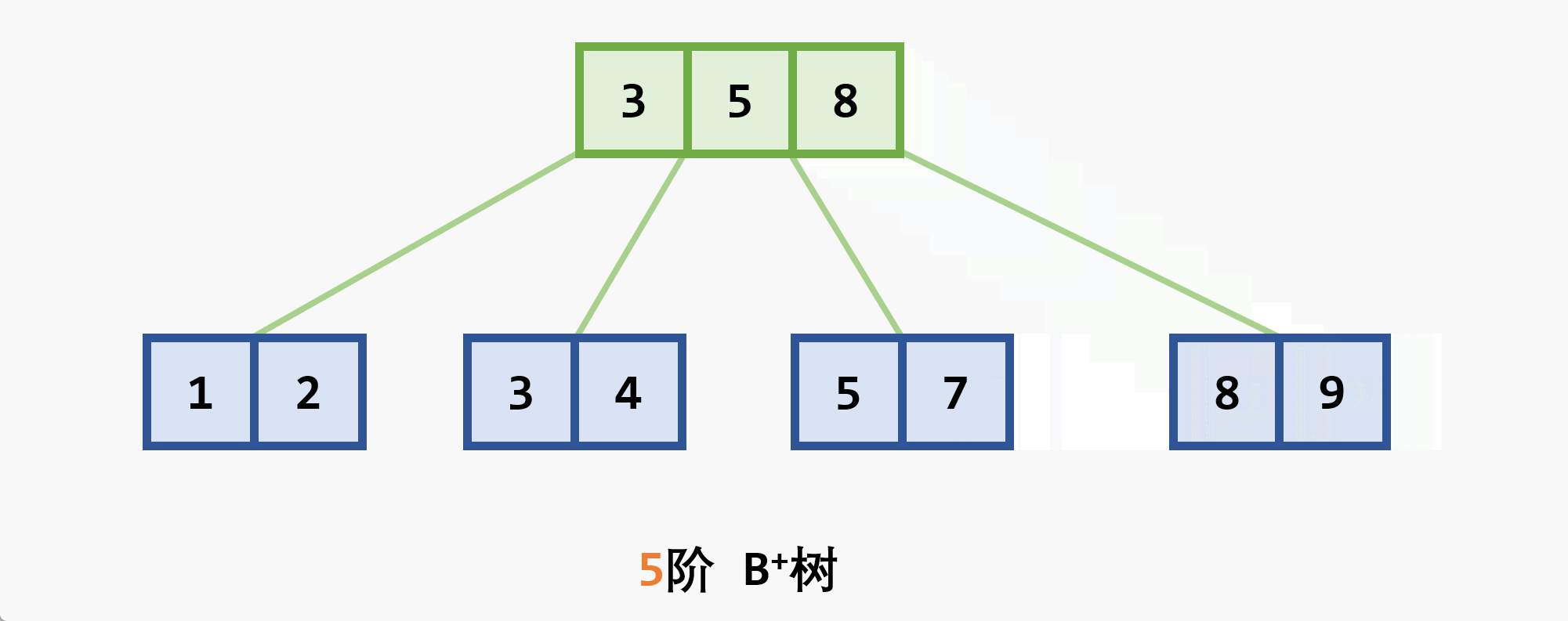
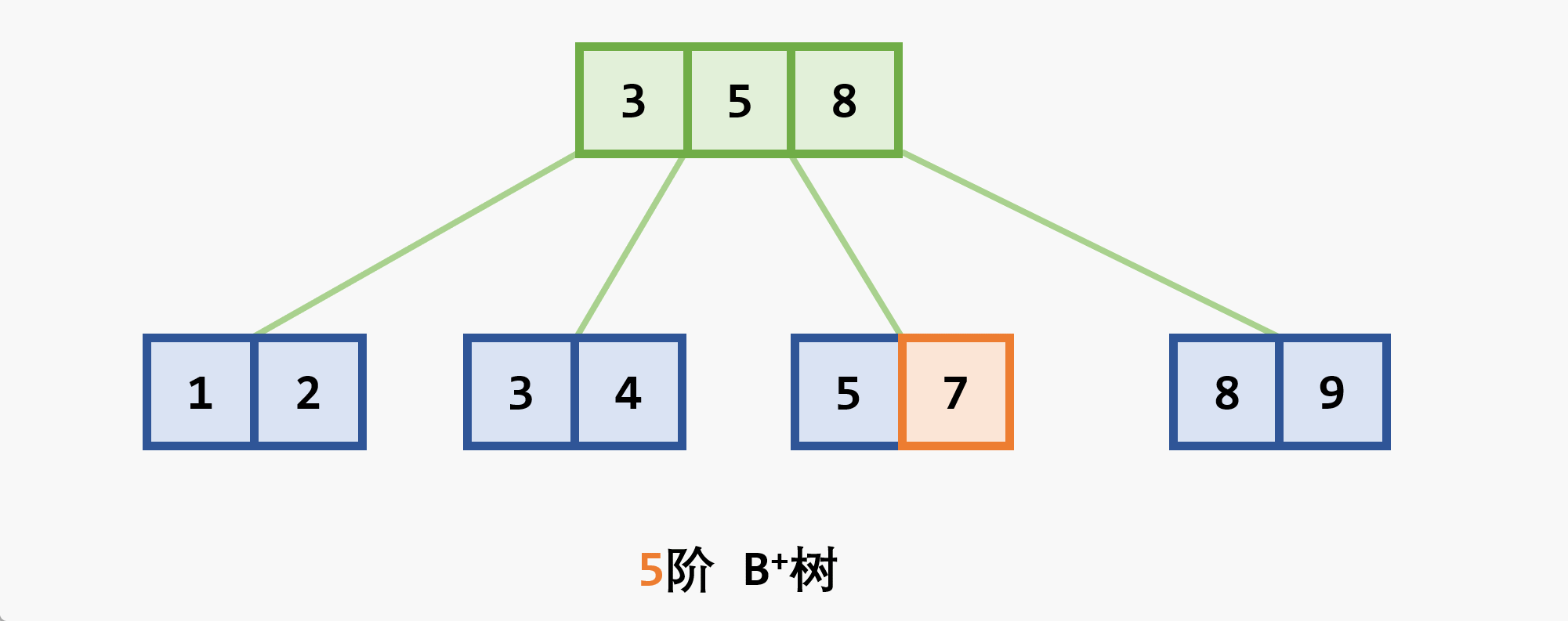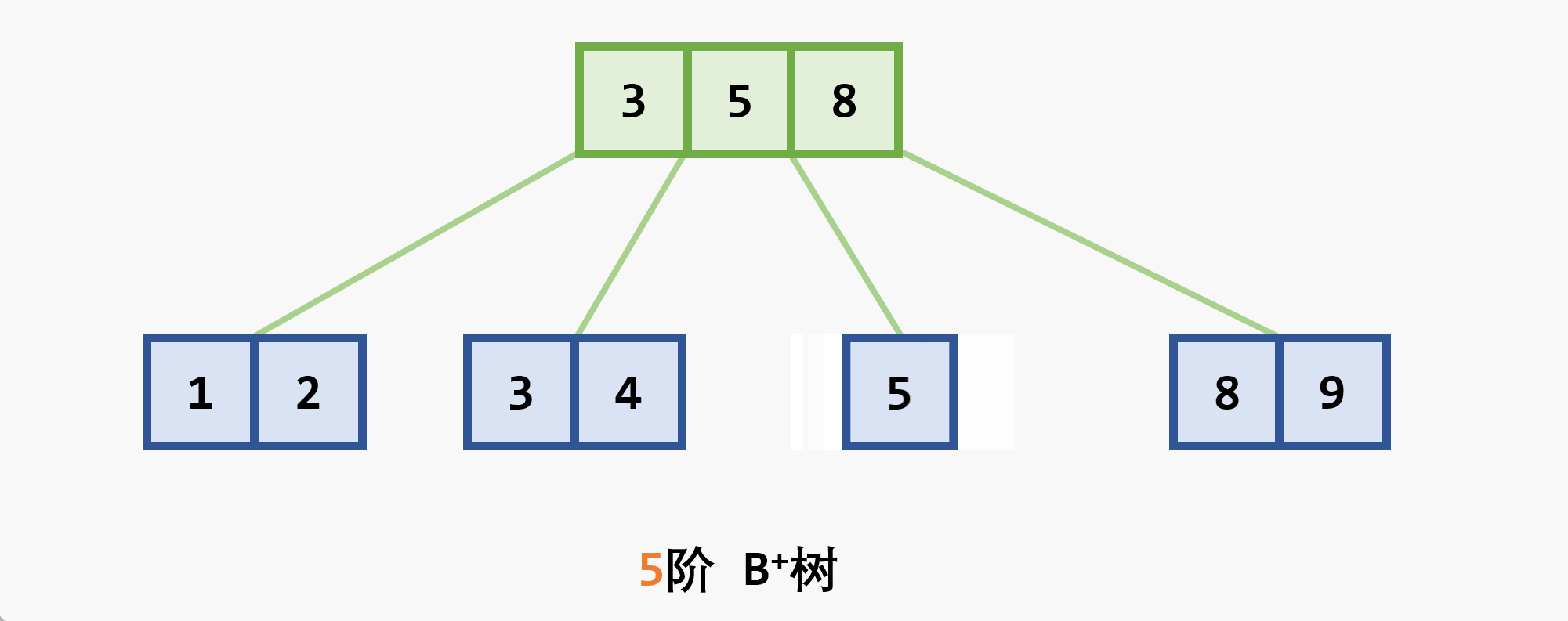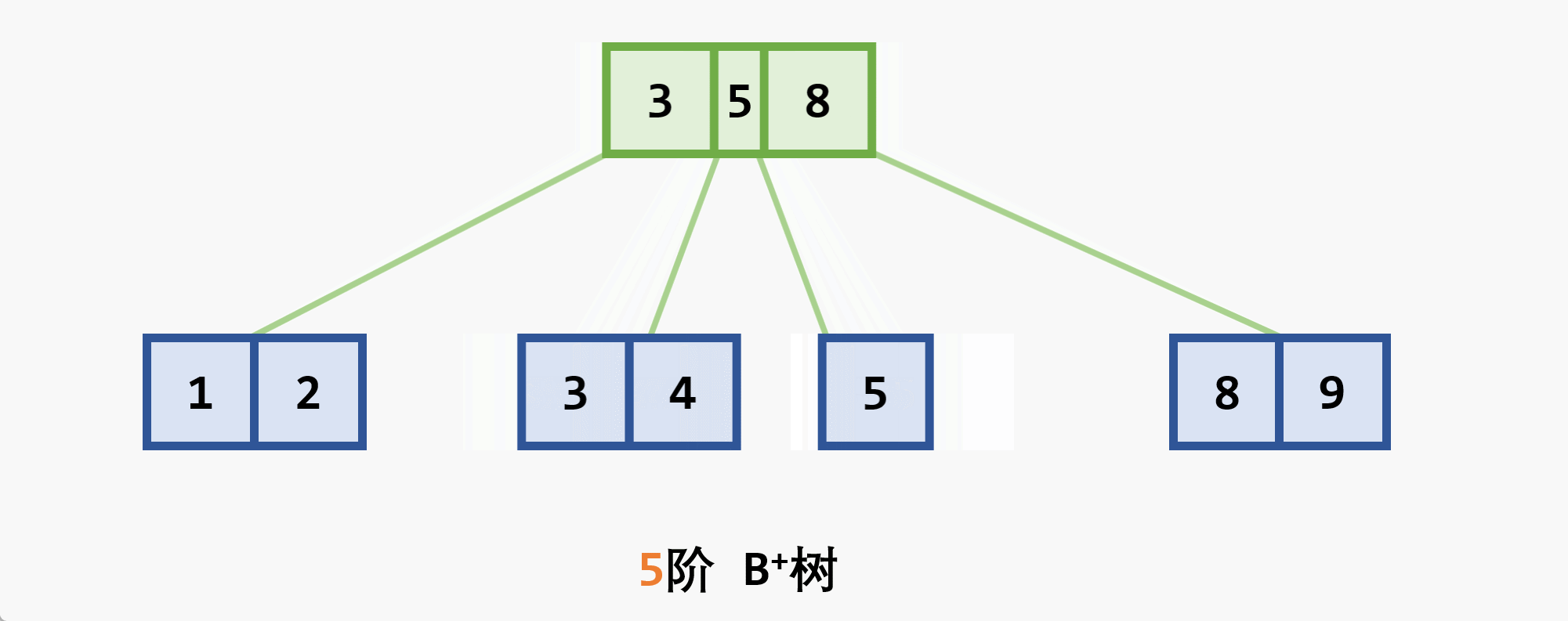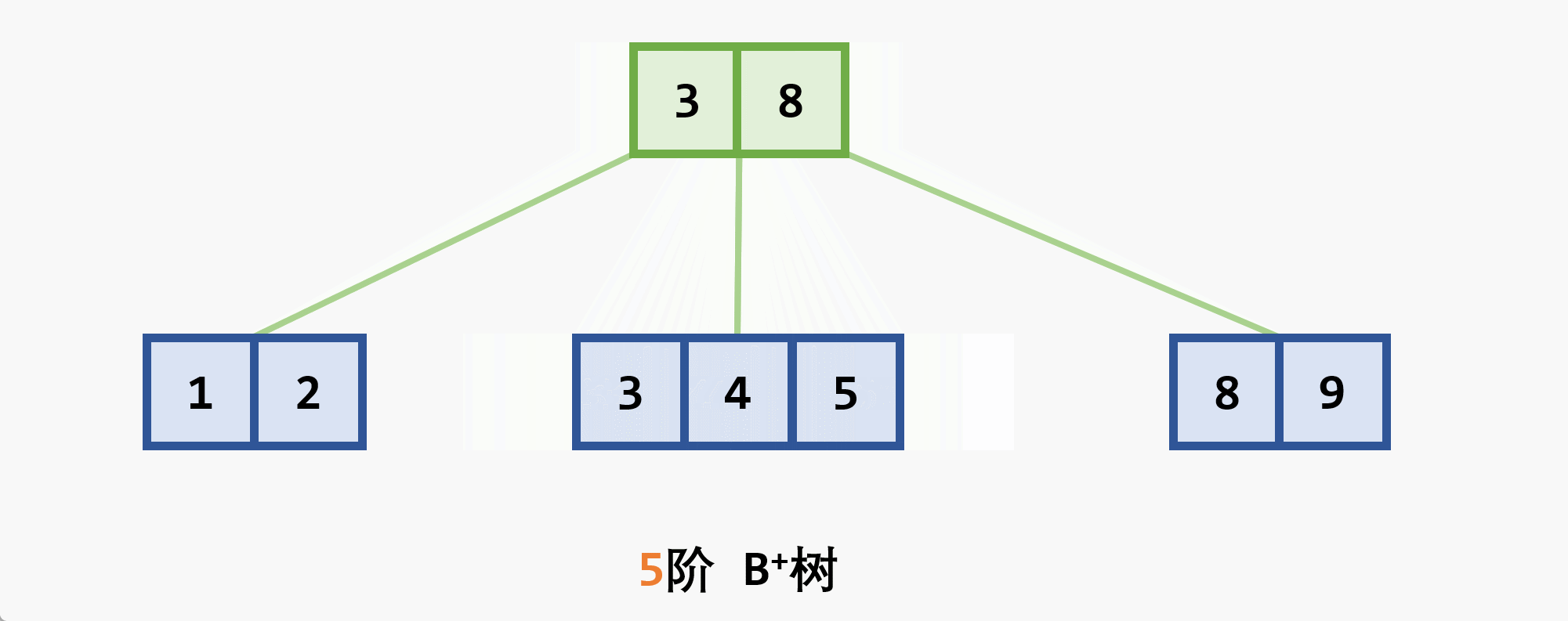
与
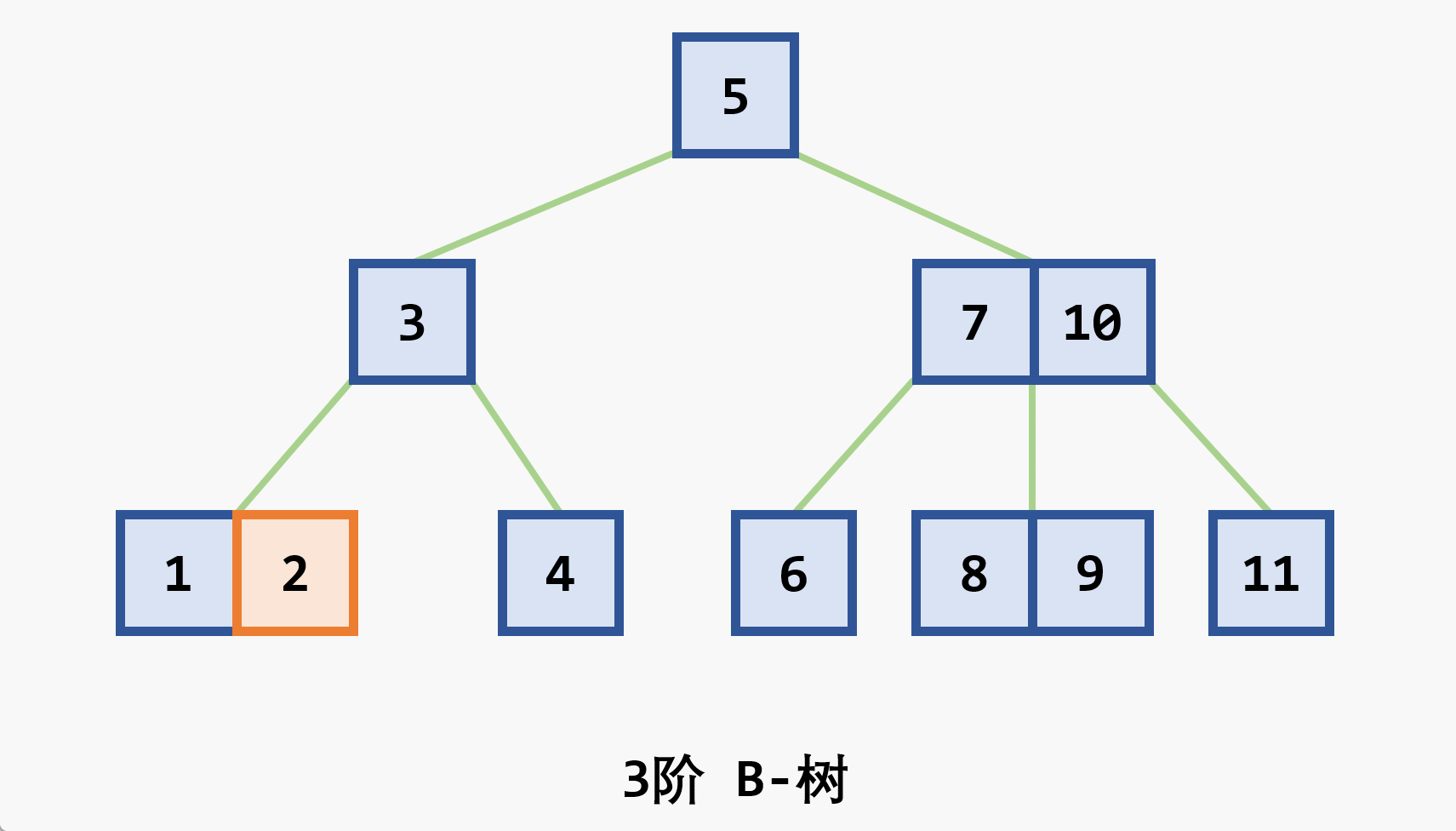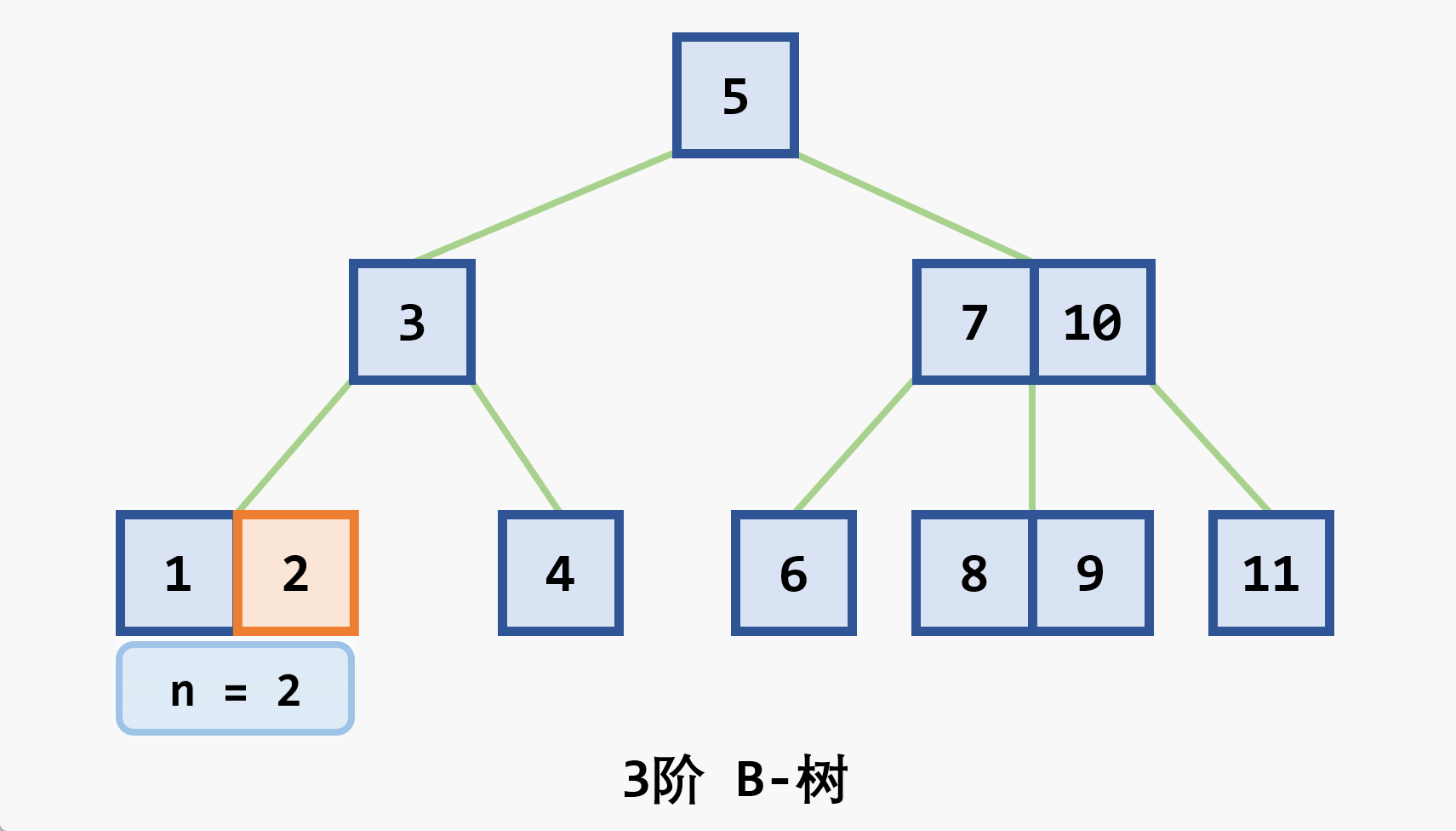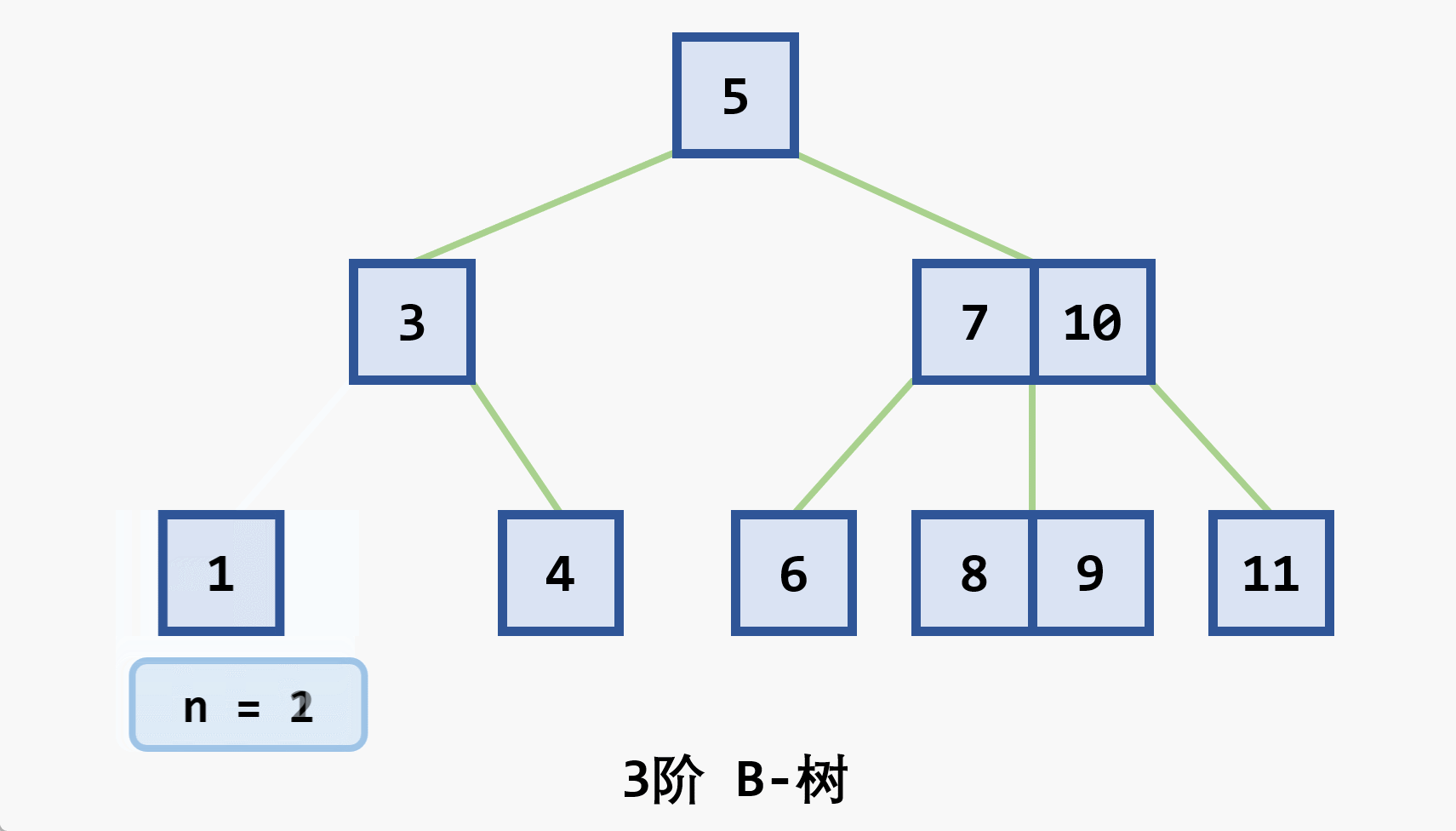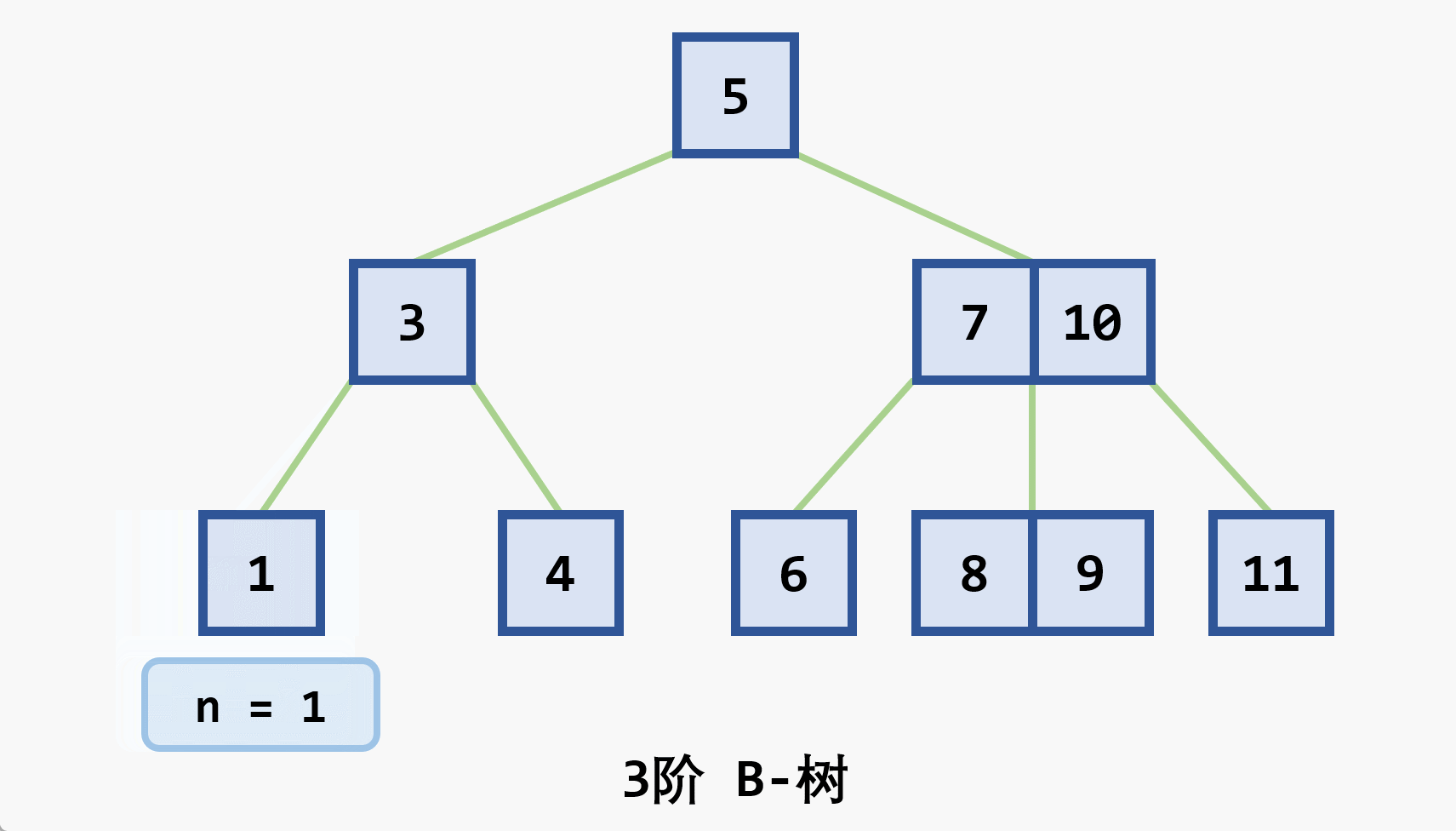
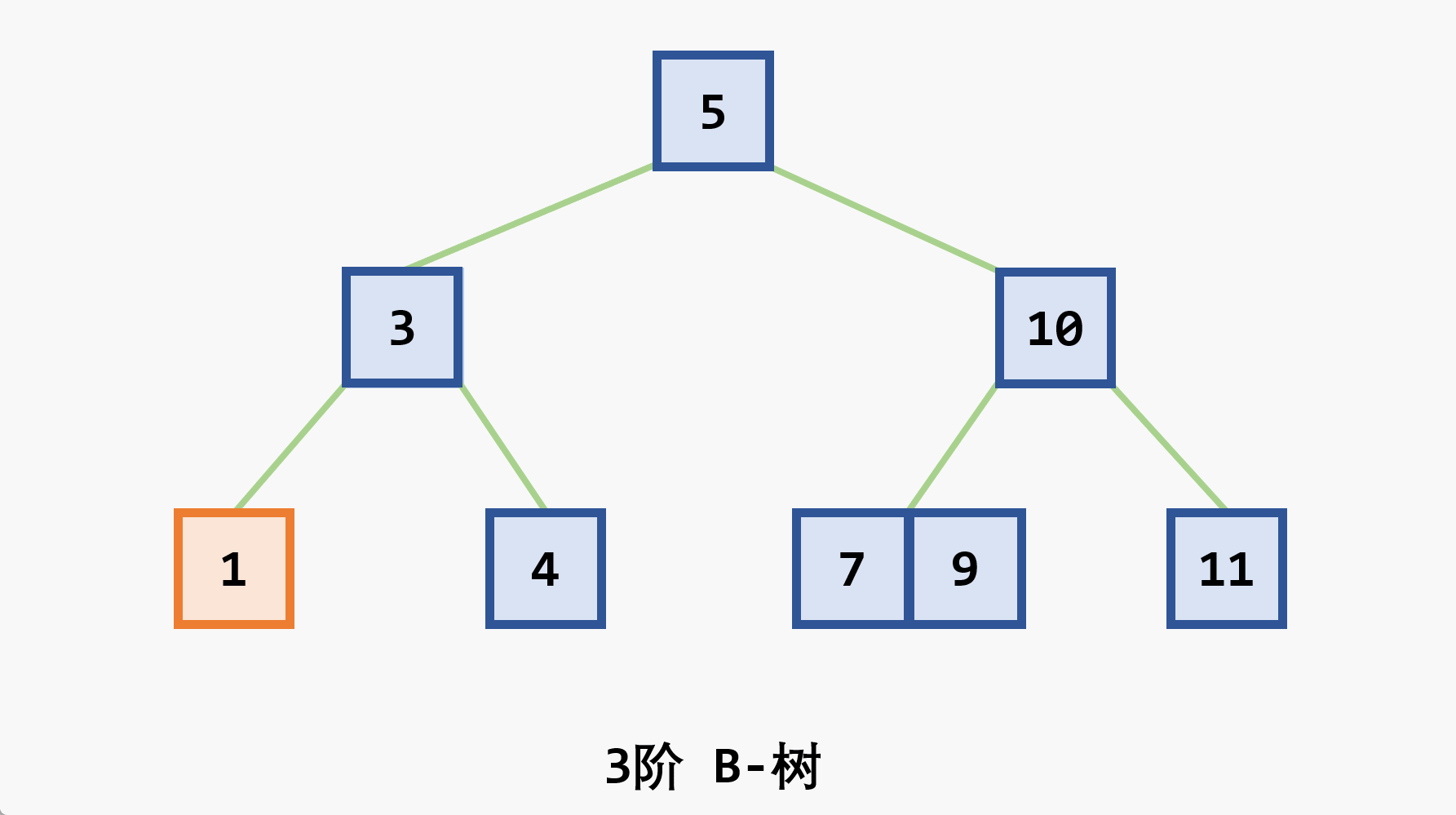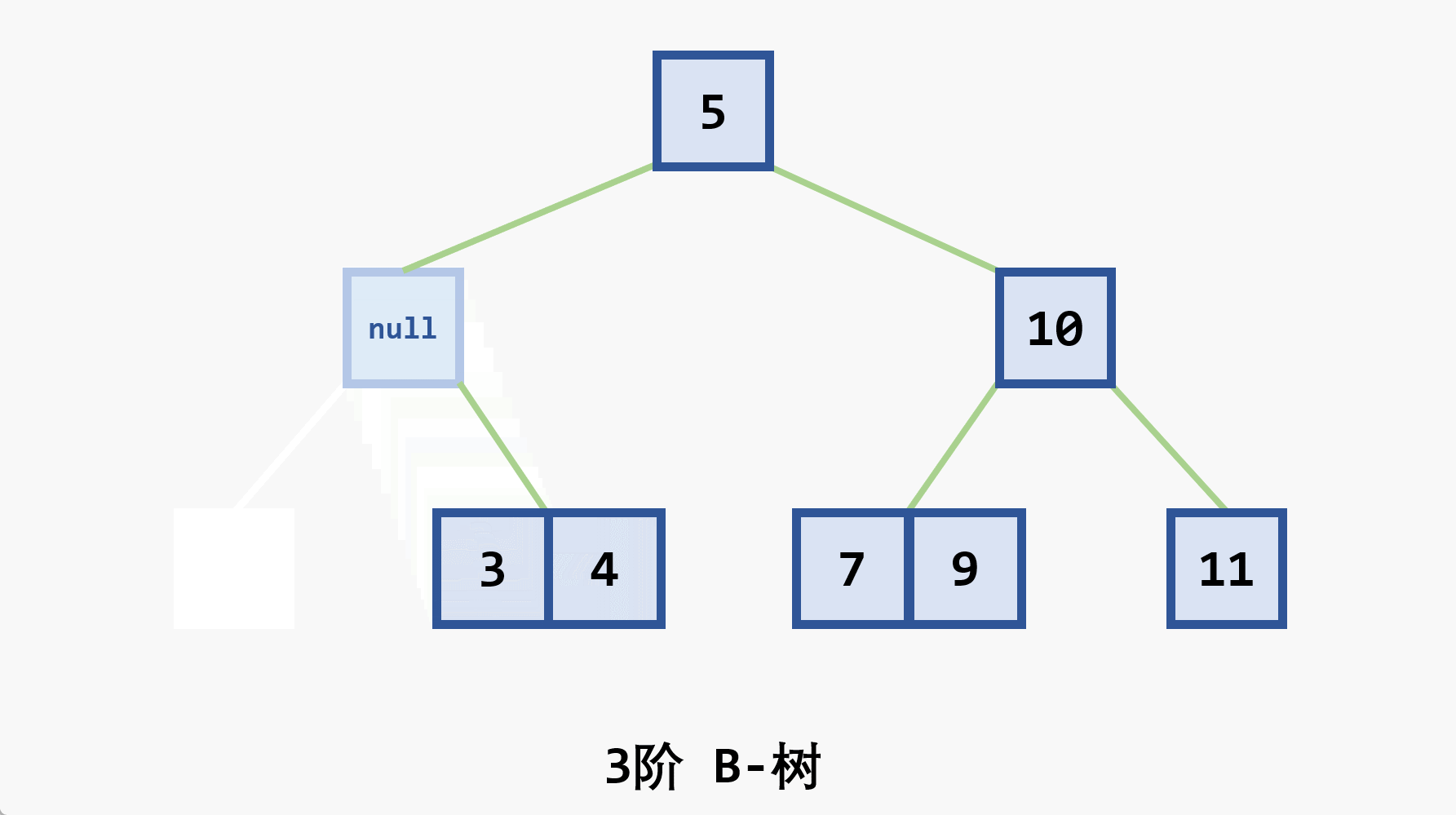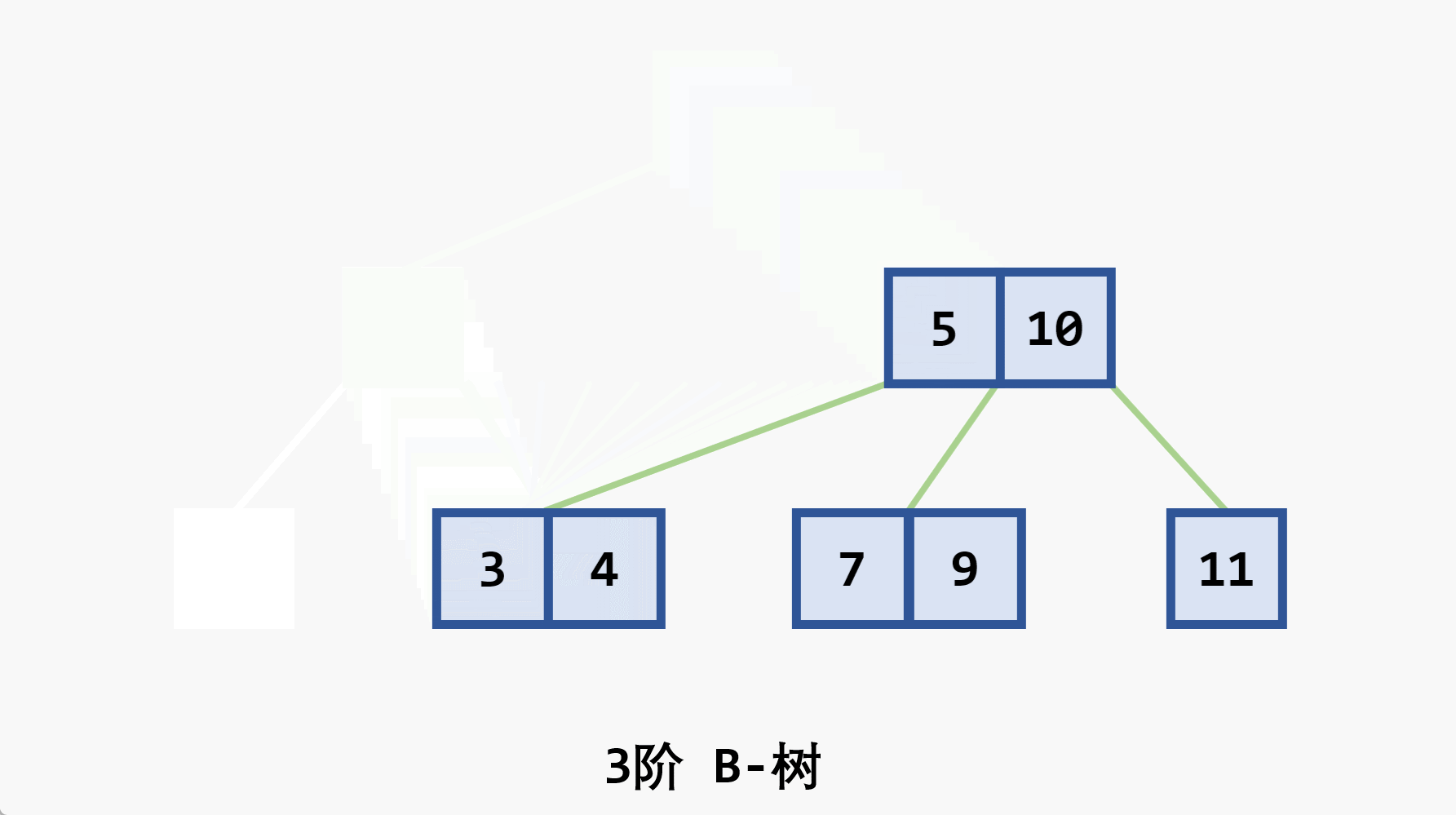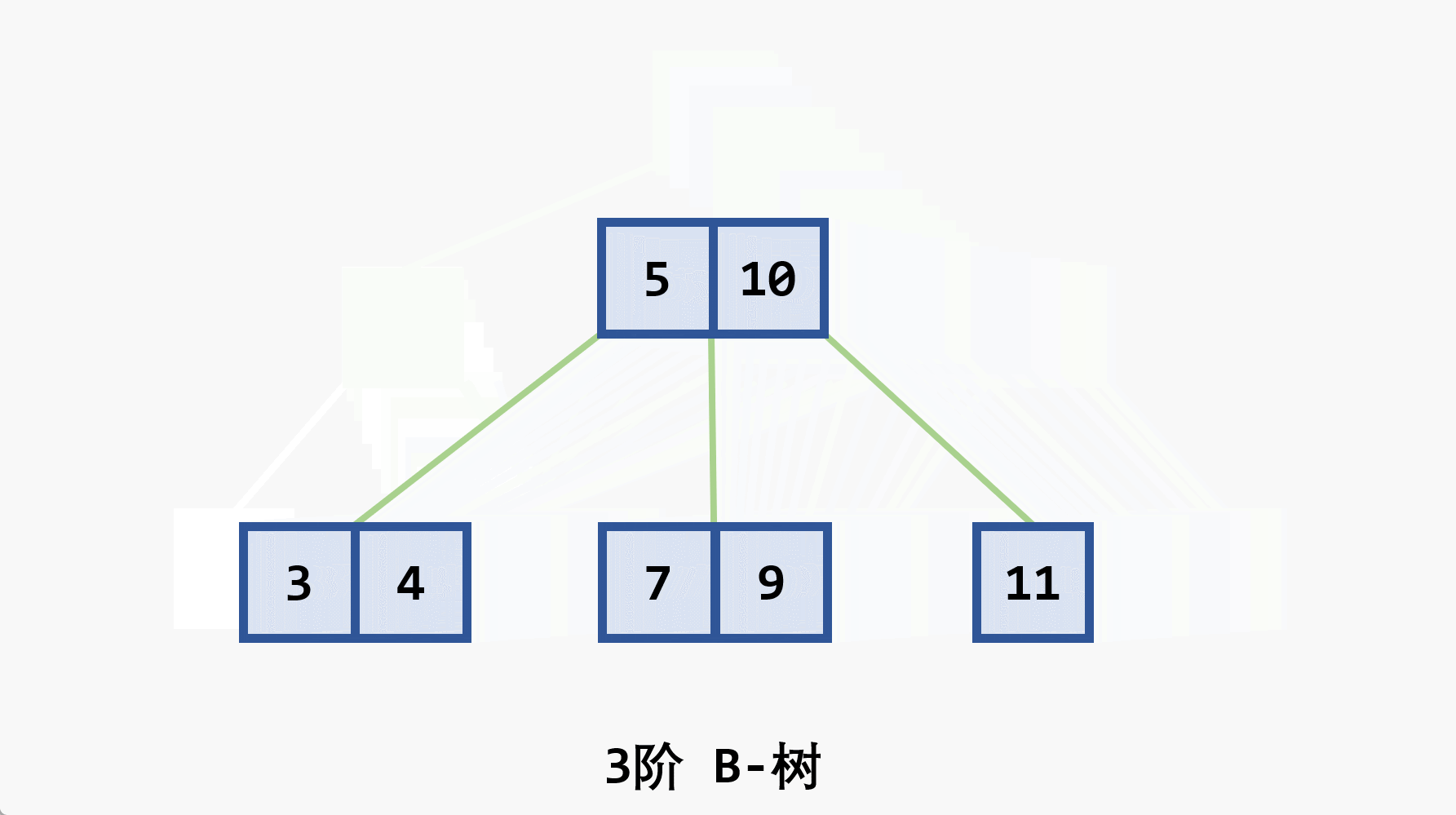
-
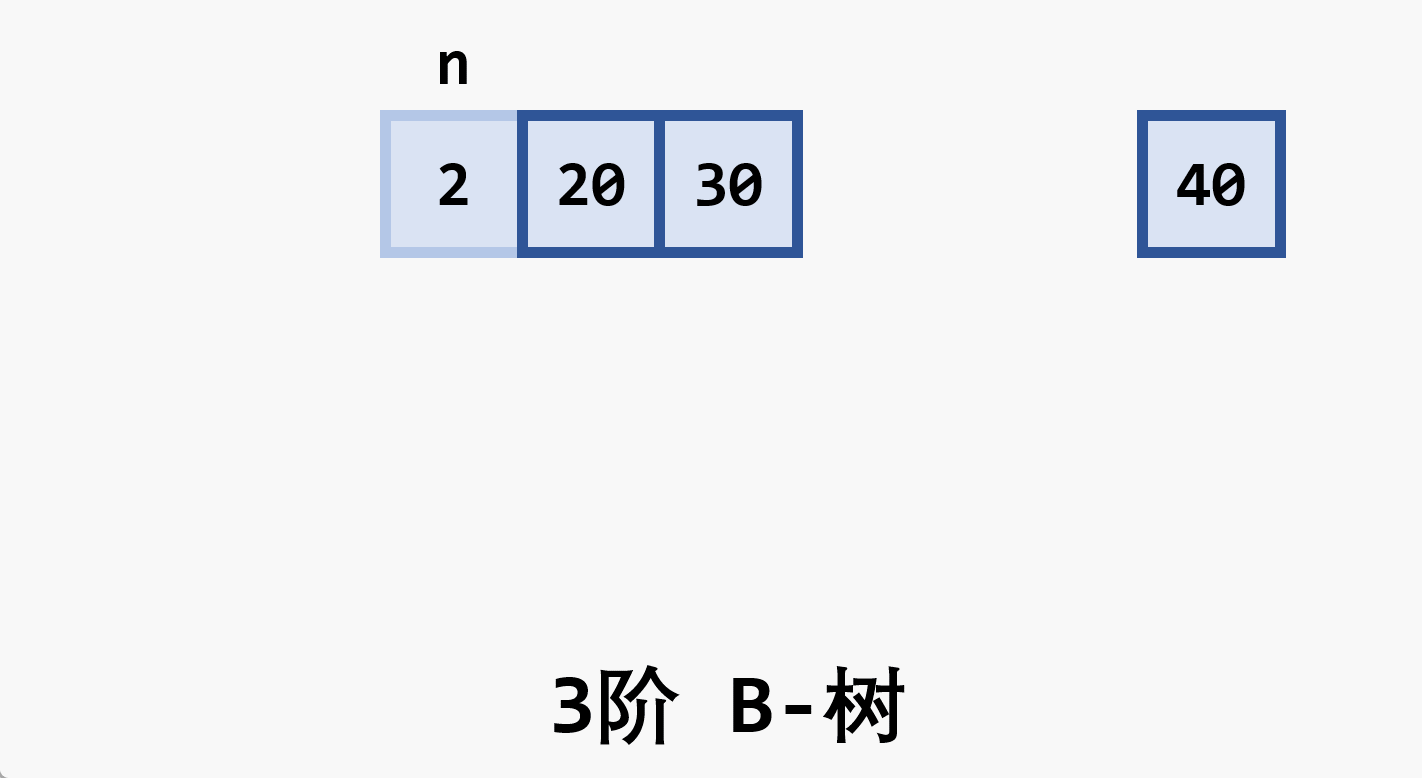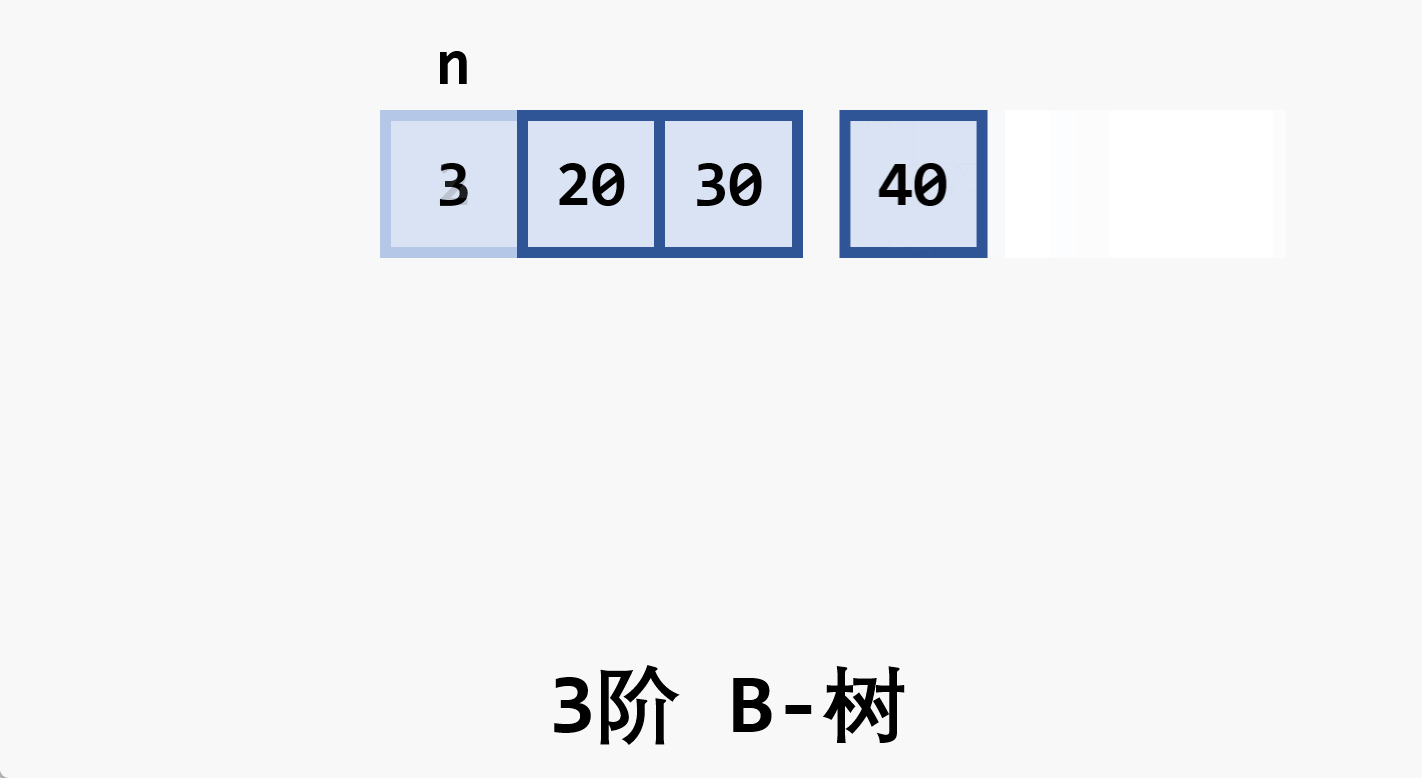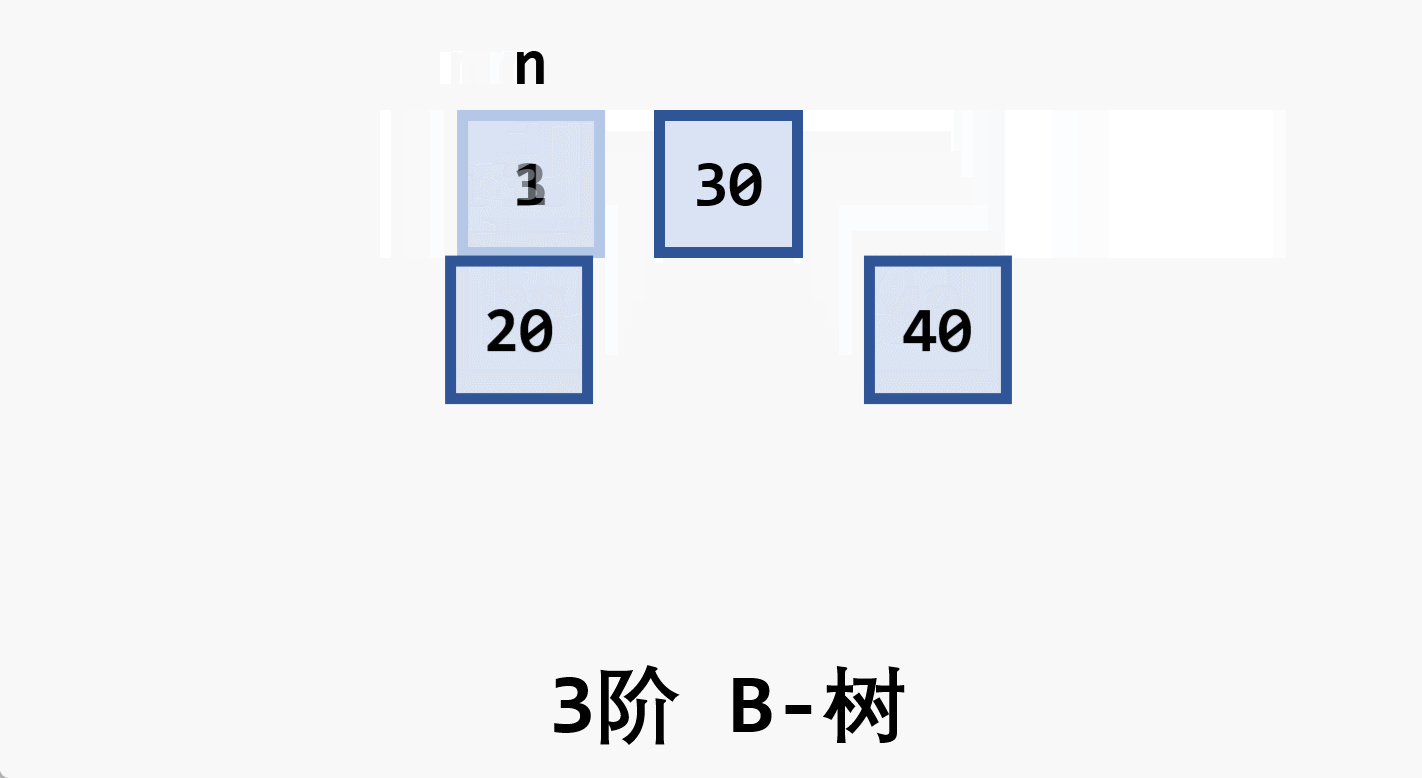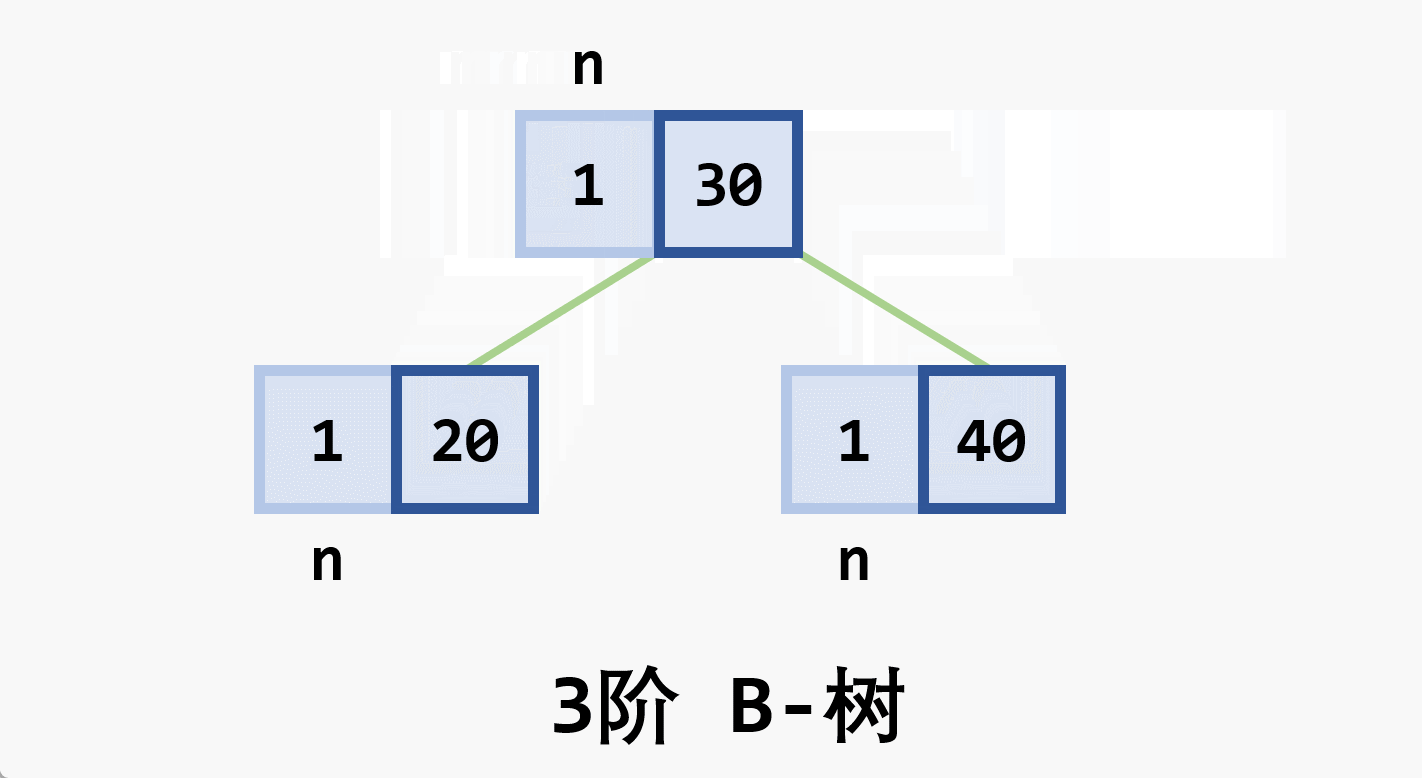
- 树中每个非叶结点 最多 有
- 根结点 (非叶结点) 至少有
- 所有的叶结点都处于同一层次上,包含了全部关键字及指向相应数据对象存放地址的指针,且叶结点本身按关键字 从小到大 顺序链接
- 每个叶结点中的子树棵数
- 若根结点同时又是叶结点,则结点格式同叶结点
- 所有的非叶结点可以看成是索引部分,结点中关键码
- 在
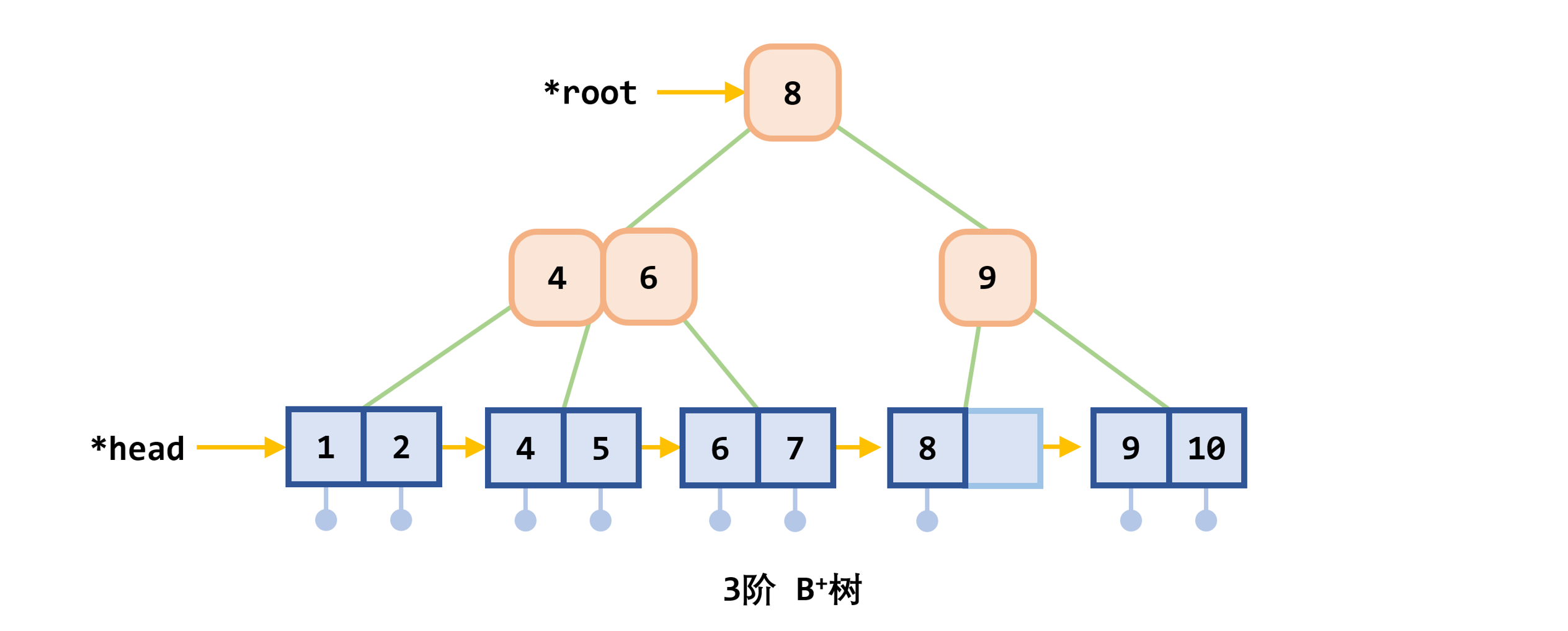
- 树中每个非叶结点 最多 有
-
- 由于与记录有关的信息存放在叶节点,查找时如果已经在上层找到了待查的关键码并不会停止,而是一直沿着指针向下查找直到叶子节点层
-
-
__EOF__
本文链接:https://www.cnblogs.com/RadiumGalaxy/p/17069404.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!

 树、二叉树等
树、二叉树等


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!