07 参数估计 | 概率论与数理统计

1. 点估计

1. 点估计

1. 点估计问题：设总体$X$的分布函数的类型为已知，但是它的某些参数是未知的，通过总体的一个样本来估计总体未知参数的值的问题称为参数的 点估计 问题
2. 点估计：设总体$X$的分布函数$F(x,\theta )$，其中$\theta$为待估计的参数，$X_1,X_2,\dots ,X_n$是$X$的一个样本，$x_1,x_2,\dots ,x_n$是相应的样本值；用样本$X_1,X_2,\dots ,X_n$构造一个适当的统计量$\hat{\theta }(X_1,X_2,\dots ,X_n)$用他的观察值$\hat{\theta }(x_1,x_2,\dots ,x_n)$作为未知参数$\theta$的 近似值，称$\hat{\theta }(X_1,X_2,\dots ,X_n)$为$\theta$的 估计量，称$\hat{\theta }(x_1,x_2,\dots ,x_n)$为$\theta$的 估计值
3. 点估计常用方法
   1. 矩估计法
   2. 极大似然估计法

2. 矩估计法

1. 基本思想：用样本矩估计总体矩，因为由大数定律知，样本的$k$阶矩依概率收敛与总体的$k$阶矩，这种用样本(原点)矩作为总体(原点)矩的估计量的方法称为 矩估计法
2. 方法：设总体$X$的分布函数为$F(x;{\theta }_1,{\theta }_2,\dots ,{\theta }_k)$，其中${\theta }_1,{\theta }_2,\dots ,{\theta }_k$为待估计参数，如果${\mu }_i=E(X^i)(i=1,2,\dots ,k)$存在，${\mu }_i$为${\theta }_1,{\theta }_2,\dots ,{\theta }_k$的函数，记${\mu }_i={\mu }_i({\theta }_1,{\theta }_2,\dots ,{\theta }_k)$，$X_1,X_2,\dots ,X_n$为总体$X$的样本，用$A_i$来估计$E(X^i)$，建立$k$个方程
   $$\{\begin{array}{c}{A}_1={\mu }_1({\theta }_1,{\theta }_2,\dots ,{\theta }_k)\\ A_2={\mu }_2({\theta }_1,{\theta }_2,\dots ,{\theta }_k)\\ \dots \\ A_k={\mu }_k({\theta }_1,{\theta }_2,\dots ,{\theta }_k)\end{array}⟹\{\begin{array}{c}\widehat{{\theta }_1}={\theta }_1(A_1,A_2,\dots ,A_k)\\ \widehat{{\theta }_2}={\theta }_2(A_1,A_2,\dots ,A_k)\\ \dots \\ \widehat{{\theta }_k}={\theta }_k(A_1,A_2,\dots ,A_k)\end{array}$$
   用$\widehat{{\theta }_i}$作为${\theta }_i$的估计量——矩估计量
3. 常见分布的矩估计量
   1. 均匀分布$X\sim U(a,b)$
      1. $\hat{a}=\bar{X}-\sqrt{\frac{3}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2}$
      2. $\hat{b}=\bar{X}+\sqrt{\frac{3}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2}$
   2. 指数分布$f(x)=\frac{1}{\theta }{e}^{-\frac{x}{\theta }}$
      1. $\hat{\theta }=\bar{X}$
   3. (0-1)分布
      1. $\hat{p}=\bar{X}$
   4. 二项分布$X\sim b(n,p)$
      $$\hat{n}=\frac{{\bar{X}}^2}{\bar{X}-\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2},\hat{p}=1-\frac{\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2}{\bar{X}}$$

   5. 正态分布$X\sim N(\mu ,{\sigma }^2)$
      1. $\hat{\mu }=\bar{X}$
      2. ${\hat{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2$
   6. 泊松分布$X\sim \pi (\lambda )$
      1. $\hat{\lambda }=\bar{X}$
      2. $\hat{\lambda }=\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2$

3. 极大似然估计法

1. 基本思想：概率最大的事件最可能出现；参数估计的极大似然法是要选取这样的值来作为参数的估计值，使得当参数取这一数值时，观测结果出现的可能性为最大
2. 似然函数
   1. 离散型：设总体$X$的分布律$P(X=x)=p(x;\theta )$，其中$\theta \in \mathrm{\Theta }$为待估计的参数，$\mathrm{\Theta }$是$\theta$可能取值的范围，设$X_1,X_2,\dots ,X_n$是来自$X$的样本，$x_1,x_2,\dots ,x_n$是样本观察值，则$(X_1,X_2,\dots ,X_n)$的联合分布率$P(X_1=x_1,X_2=x_2,\dots ,X_n=x_n)=\prod _{i=1}^{n}p(x_i;\theta )$，对固定的样本观察值$x_1,x_2,\dots ,x_n$，它是未知参数的函数，记为$L(\theta )=L(x_1,x_2,\dots ,x_n;\theta )=\prod _{i=1}^{n}p(x_i;\theta ),\theta \in \mathrm{\Theta }$，称之为样本的 似然函数
   2. 连续型：设总体$X$的概率密度函数为$f(x;\theta ),\theta \in \mathrm{\Theta }$为未知参数，此时样本的似然函数为$L(\theta )=L(x_1,x_2,\dots ,x_n;\theta )=\prod _{i=1}^{n}f(x_i;\theta ),\theta \in \mathrm{\Theta }$
3. 最大似然估计：如果存在$\hat{\theta }=\hat{\theta }(x_1,x_2,\dots ,x_n)$，使得$L(\hat{\theta })=\underset{\theta \in \mathrm{\Theta }}{max}L(\theta )$，则称$\hat{\theta }(x_1,x_2,\dots ,x_n)$为$\theta$的 最大似然估计值，$\hat{\theta }(X_1,X_2,\dots ,X_n)$的 最大似然估计量
4. 如何求$L(\theta )$的最大值
   1. 根据函数的单调性分析
   2. 对数似然方程：由于$L(\theta )$和$\ln L(\theta )$在$\mathrm{\Theta }$上有相同的最大值点，因此可以求$\ln L(\theta )$关于$\theta$的最大值点，当$\ln L(\theta )$关于$\theta$可微时，必然满足方程$\frac{\partial \ln L({\theta }_i)}{\partial {\theta }_i},(i=1,2,\dots ,k)$，然后确定其为最大值点
5. 常见分布的最大似然估计量
   1. (0-1)分布
      1. $\hat{p}=\bar{X}$
   2. 正态分布$X\sim N(\mu ,{\sigma }^2)$
      1. $\hat{\mu }=\bar{X}$
      2. ${\hat{\sigma }}^2=\frac{1}{n}\sum _{i=1}^n(X_i-\bar{X}{)}^2$
   3. 均匀分布$X\sim U(a,b)$
      1. $\hat{a}=\underset{1\le i\le n}{min}{X}_i$
      2. $\hat{b}=\underset{1\le i\le n}{max}{X}_i$
   4. 指数分布$f(x)=\frac{1}{\theta }{e}^{-\frac{x}{\theta }}$
      1. $\hat{\theta }=\bar{X}$
   5. 泊松分布$X\sim \pi (\lambda )$
      1. $\hat{\lambda }=\bar{X}$

4. 矩估计和极大似然估计的联系和区别

1. 极大似然法克服了矩估计法的一些缺点， 它利用总体的样本和分布函数表达形式所提供的信息建立未知参数的估计量， 同时它也不要求总体原点矩存在
2. 极大似然估计量一般要解似然方程，而有时解似然方程很困难，只能用数值方法求似然方程的近似解
3. 在统计问题中往往先使用最大似然估计法，在最大似然估计法使用不方便时，再用矩估计法

2. 估计量的评选标准

1. 无偏性

1. 引入原因：估计量是随机变量，对于不同的样本值会得到不同的估计值. 我们希望估计值在未知参数真值附近摆动，而它的期望值等于未知参数的真值. 这就出现了无偏性这个标准
2. 无偏估计量：如果估计量$\hat{\theta }=\theta (X_1,X_2,\dots ,X_n)$的数字期望$E(\hat{\theta })$存在，且对于任意$\theta \in \mathrm{\Theta }$有$E(\hat{\theta })=\theta$，则称$\hat{\theta }$是$\theta$的 无偏估计量

2. 有效性

1. 引入原因：用$\hat{\theta }$估计$\theta$时，仅具有无偏性是不够的，我们希望$\hat{\theta }$的取值能集中于$\theta$附近，而且密集的程度越高越好；方差是描述随机变量取值的集中程度的，所以无偏估计以方差小者为好，因此提出所谓 有效性 标准
2. 有效：设$\widehat{{\theta }_1}$与$\widehat{{\theta }_2}$都是参数$\theta$的无偏估计，若$D(\widehat{{\theta }_1})\le D(\widehat{{\theta }_2})$，则称$\widehat{{\theta }_1}$较$\widehat{{\theta }_2}$ 有效

3. 相合性

1. 引入原因：无偏性和有效性是在样本容量$n$一定的情况下对估计量提出的要求，一个好的估计量$\hat{\theta }$，当样本容量增大时， $\hat{\theta }$的取值与参数$\theta$ 的真值任意接近的可能性应该更大，因此，还有所谓 一致性 标准
2. 相合估计量：设$\widehat{{\theta }_n}$是未知参数$\theta$的估计量，如果对于$\mathrm{\forall }\epsilon >0$，有
   $$\underset{n\to \mathrm{\infty }}{lim}P(|\hat{\theta }-\theta |<\epsilon )=1$$
   则称$\hat{\theta }$为$\theta$的 相合估计量，即$\hat{\theta }\stackrel{P}{\to }\theta$
3. 定理：若$\widehat{{\theta }_n}$ 是$\theta$ 的无偏估计量，且当$n\to \mathrm{\infty }$时，$D(\widehat{{\theta }_n})\to 0$则$\widehat{{\theta }_n}$ 是$\theta$ 的 相合估计量

3. 区间估计

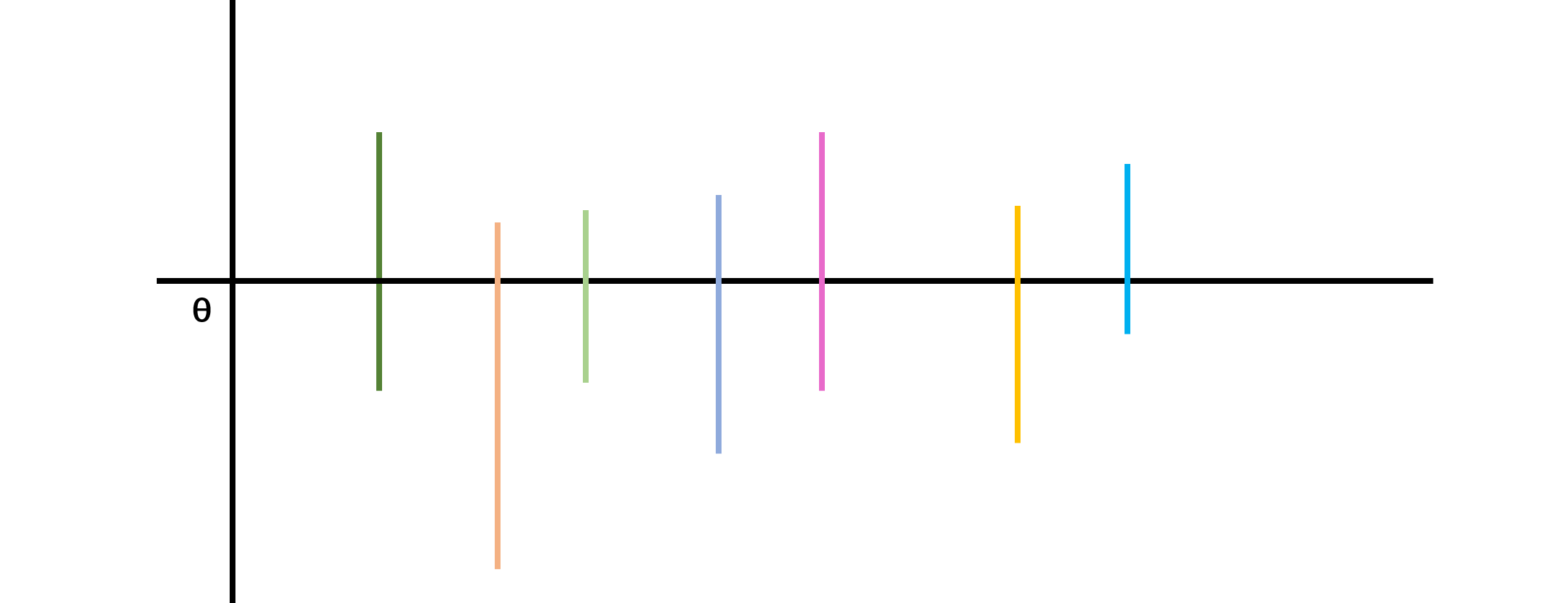
1. 置信区间的概念

1. 置信区间：设总体$X$的分布函数$F(x;\theta )$，其中$\theta$为未知参数，$X_1,X_2,\dots ,X_n$是取自总体的样本，对给定值$\alpha (0<\alpha <1)$，如果存在统计量${\theta }_1,{\theta }_2$满足$P({\theta }_1<\theta <{\theta }_2)\ge 1-\alpha$，则称随机区间$({\theta }_1,{\theta }_2)$为$\theta$置信水平 为$1-\alpha$的置信区间，${\theta }_1,{\theta }_2$分别称为置信度为$1-\alpha$的 双侧置信下限和 置信上限
2. 评价置信区间好坏标准
   1. 精度：${\theta }_2-{\theta }_1$越小越好
   2. 置信度：$P({\theta }_1<\theta <{\theta }_2)$越大越好
3. 置信度与估计精度
   1. 估计精度：置信区间的长度${\theta }_2-{\theta }_1$
   2. 置信度与估计精度是一对矛盾的量
      1. 置信水平高，则区间大，区间精度差
      2. 置信区间小，则精度高，但置信水平低
      3. 一般准则：在保证置信度的条件下尽可能提高精度

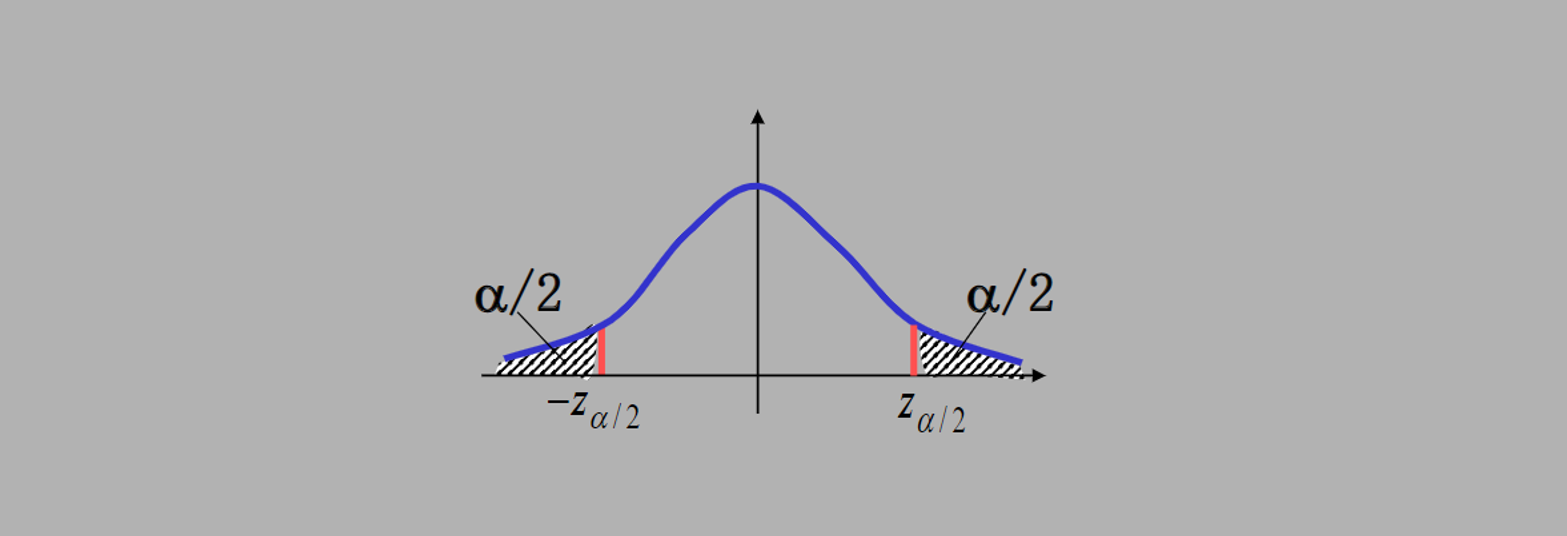
2. 寻求置信区间的方法

1. 基本思想：在点估计的基础上，构造合适的含样本及待估参数的函数$U$，且已知 $U$ 的分布，再根据给定的置信度导出待估参数置信区间
2. 一般步骤
   1. 选取未知参数$\theta$ 的某个较优估计量$\hat{\theta }$（如无偏估计）
   2. 围绕$\hat{\theta }$构造一个与待估参数$\theta$有关的函数$U$, 且分布已知
   3. 对给定的置信水平$1-\alpha$，确定${\lambda }_1$与${\lambda }_2$，使$P({\lambda }_1<U<{\lambda }_2)=1-\alpha$
   4. 对上式作恒等变形，化为$P({\theta }_1<\theta <{\theta }_2)=1-\alpha$，则$({\theta }_1,{\theta }_2)$就是$\theta$的置信水平为$1-\alpha$的置信区间

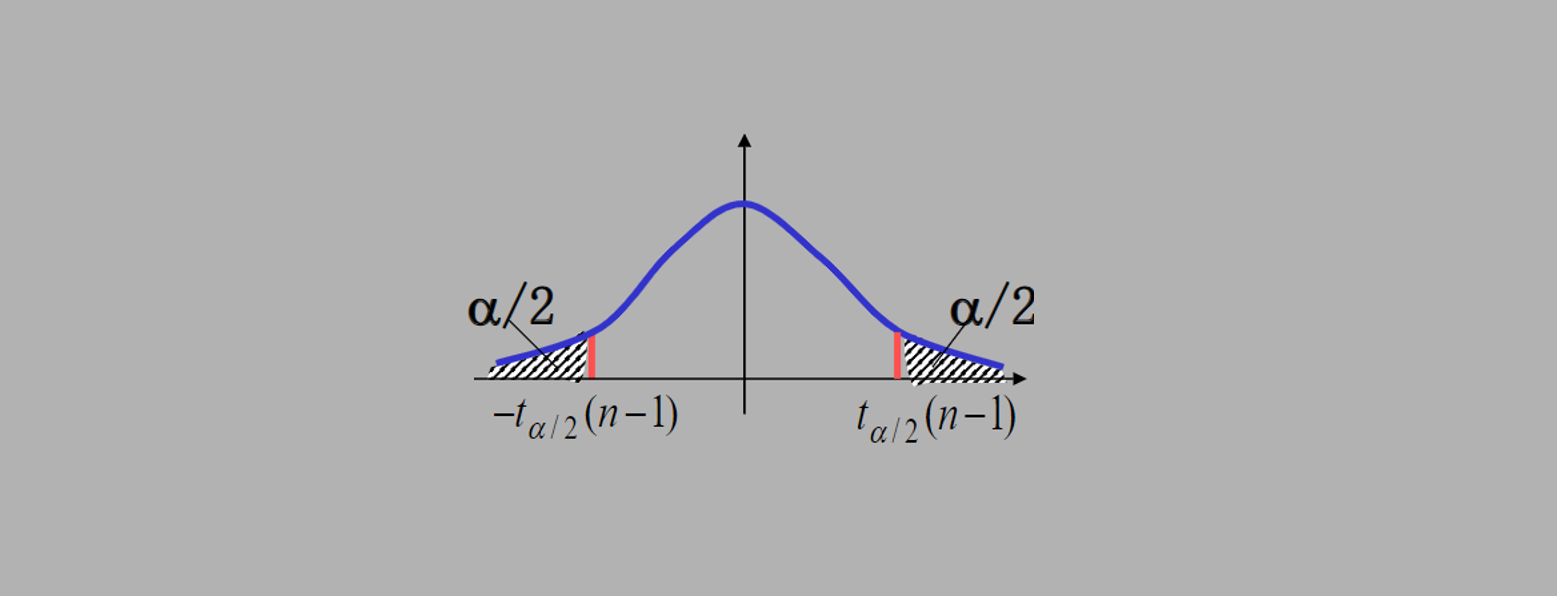
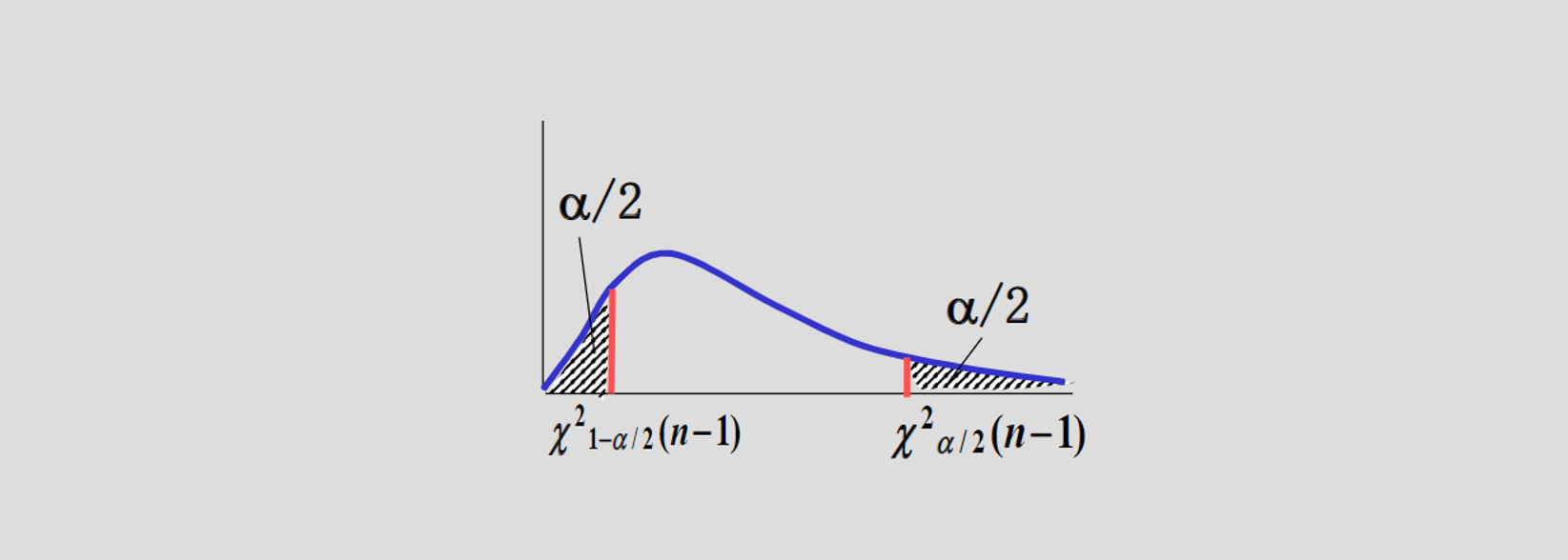
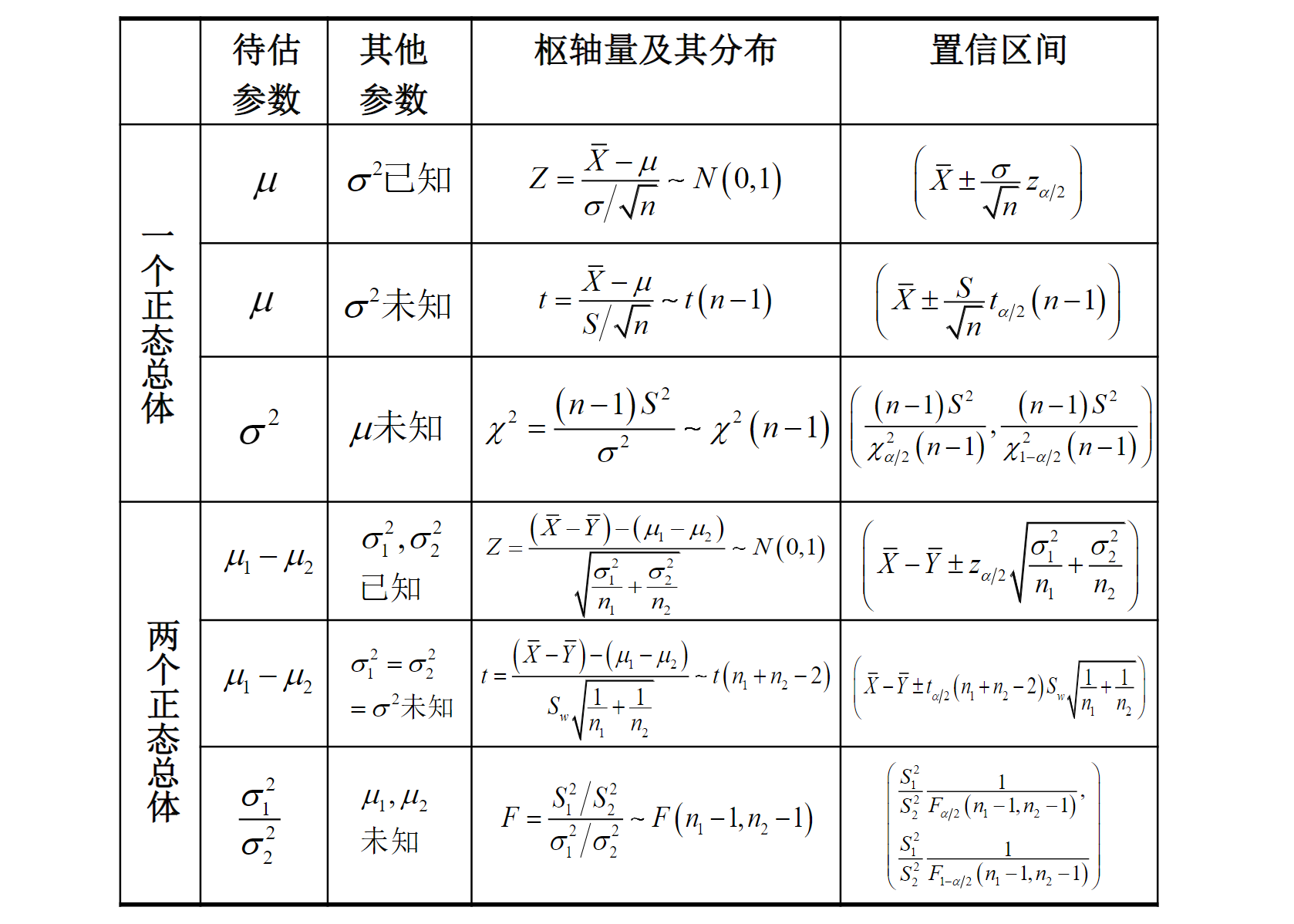
4. 正态总均值与方差的区间估计

1. 单个正态总体

1. 均值$\mu$的置信区间

   1. ${\sigma }^2$已知：$\mu$的置信度水平为$1-\alpha$的置信区间（$\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}\sim N(0,1)$）

      $$(\bar{X}-\frac{\sigma }{\sqrt{n}}{z}_{\alpha /2},\bar{X}+\frac{\sigma }{\sqrt{n}}{z}_{\alpha /2})$$

      

   2. ${\sigma }^2$未知：$\mu$的置信度水平为$1-\alpha$的置信区间（$\frac{\bar{X}-\mu }{S/\sqrt{n}}\sim t(0,1)$）

      $$(\bar{X}-\frac{S}{\sqrt{n}}{t}_{\alpha /2}(n-1),\bar{X}+\frac{S}{\sqrt{n}}{t}_{\alpha /2}(n-1))$$

      

2. 方差${\sigma }^2$的置信区间（$\mu$未知）：$\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$

   $$(\frac{(n-1)S^2}{{\chi }_{\alpha /2}^2(n-1)},\frac{(n-1)S^2}{{\chi }_{1-\alpha /2}^2(n-1)})$$

   

2. 两个正态总体

1. 两个总体均值差${\mu }_1-{\mu }_2$的置信区间
   1. ${\sigma }_1^2,{\sigma }_2^2$已知：${\mu }_1-{\mu }_2$的置信区间
      $$(\bar{X}-\bar{Y}-z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}},\bar{X}-\bar{Y}+z_{\alpha /2}\sqrt{\frac{{\sigma }_1^2}{n_1}+\frac{{\sigma }_2^2}{n_2}})$$

   2. ${\sigma }_1^2={\sigma }_2^2={\sigma }^2$，但是${\sigma }^2$未知：${\mu }_1-{\mu }_2$的置信区间
      $$(\bar{X}-\bar{Y}\pm t_{\alpha /2}(n_1+n_2-2)S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}})$$
      其中
      $$S_w^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}$$

2. 两个总体方差比${\sigma }_1^2/{\sigma }_2^2$
   1. 置信区间：${\mu }_1,{\mu }_2$未知：$\frac{S_1^2/{\sigma }_1^2}{S_2^2/{\sigma }_2^2}\sim F(n_1-1,n_2-1)$
      $$(\frac{S_1^2}{S_2^2}\frac{1}{F_{\alpha /2}(n_1-1,n_2-1)},\frac{S_1^2}{S_2^2}\frac{1}{F_{1-\alpha /2}(n_1-1,n_2-1)})$$

3. 正态总体均值、方差的置信区间总结

5. (0-1)分布参数的区间估计

1. (0-1)分布参数的区间估计

1. (0-1)分布参数的区间估计：设总体$X\sim b(1,p)$，$p$为未知参数，$X$的分布律为$f(x;p)=p^x(1-p{)}^{1-x},x=0,1$，取$X_1,X_2,\dots ,X_n(n>50)$作为$X$的大样本，已知(0-1)分布的均值和方差分别为$\mu =p,{\sigma }^2=p(1-p)$，则由中心极限定理
   $$\frac{\sum _{i=1}^n{X}_i-np}{\sqrt{np(1-p)}}=\frac{n\bar{X}-np}{\sqrt{np(1-p)}}\stackrel{\mathrm{近}\mathrm{似}}{\sim }N(0,1)$$
   于是有枢轴量
   $$P(-z_{\alpha /2}<\frac{n\bar{X}-np}{\sqrt{np(1-p)}}<z_{\alpha /2})\approx 1-\alpha$$

2. $p$的近似置信度为$1-\alpha$置信区间为$(p_1,p_2)$，其中$p_1=\frac{1}{2a}(-b-\sqrt{b^2-4ac}),p_2=\frac{1}{2a}(-b+\sqrt{b^2-4ac})$
   由
   $$(n+z_{\alpha /2}^2)p^2-(2n\bar{X}+z_{\alpha /2}^2)p+n{\bar{X}}^2<0$$
   得到，记
   $$a=n+z_{\alpha /2}^2,b=-(2n\bar{X}+z_{\alpha /2}^2),c=n{\bar{X}}^2$$

6. 单侧置信区间

1. 单侧置信区间

1. 单侧置信下限：对于给定值$\alpha (0<\alpha <1)$，如果由样本$X_1,X_2,\dots ,X_n$确定的统计量$\underset{―}{\theta }=\underset{―}{\theta }(X_1,X_2,\dots ,X_n),$对$\mathrm{\forall }\theta \in \mathrm{\Theta }$满足$P(\theta >\underset{―}{\theta })=1-\alpha$，成随机区间$(\underset{―}{\theta },+\mathrm{\infty })$是$\theta$的置信水平为$1-\alpha$的 单侧置信区间，$\underset{―}{\theta }$称为$\theta$的置信水平为$1-\alpha$的 单侧置信下限
2. 单侧置信上限：对于给定值$\alpha (0<\alpha <1)$，如果由样本$X_1,X_2,\dots ,X_n$确定的统计量$\bar{\theta }=\bar{\theta }(X_1,X_2,\dots ,X_n),$对$\mathrm{\forall }\theta \in \mathrm{\Theta }$满足$P(\theta <\bar{\theta })=1-\alpha$，成随机区间$(-\mathrm{\infty },\bar{\theta })$是$\theta$的置信水平为$1-\alpha$的 单侧置信区间，$\bar{\theta }$称为$\theta$的置信水平为$1-\alpha$的 单侧置信上限

2. 常见单侧置信区间

__EOF__

本文作者：RadiumGalaxy
本文链接：https://www.cnblogs.com/RadiumGalaxy/p/16974392.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！