02 轨迹与方程 | 解析几何
1. 平面曲线的方程
1. 曲线的方程
- 曲线的定义:平面上的曲线,是具有某种特征性质的点的集合;具体说,曲线上点的特征性质包含如下两方面要求
- 曲线上的点都具有这些性质
- 具有这些性质的点都在曲线上
- 曲线的方程:
2. 曲线的一般方程
- 一般方程:
- 求解:通常通过点的某些共同性质写出曲线的一般方程
3. 曲线的参数方程
-
参数方程
- 向量式参数方程:
- 坐标式参数方程
- 向量式参数方程:
-
求解:有些曲线上动点的运动规律,不是直接反映为动点的两个坐标
-
一般方程和曲线方程的转换
- 曲线的一般方程能够转化成参数方程
- 将参数方程不一定能转化成一般方程
- 选取参数的时候注意参数取到的值要保证互化的方程形式等价,不能放大或者缩小值的域
-
旋轮线(摆线):取直角坐标系, 设半径为
-
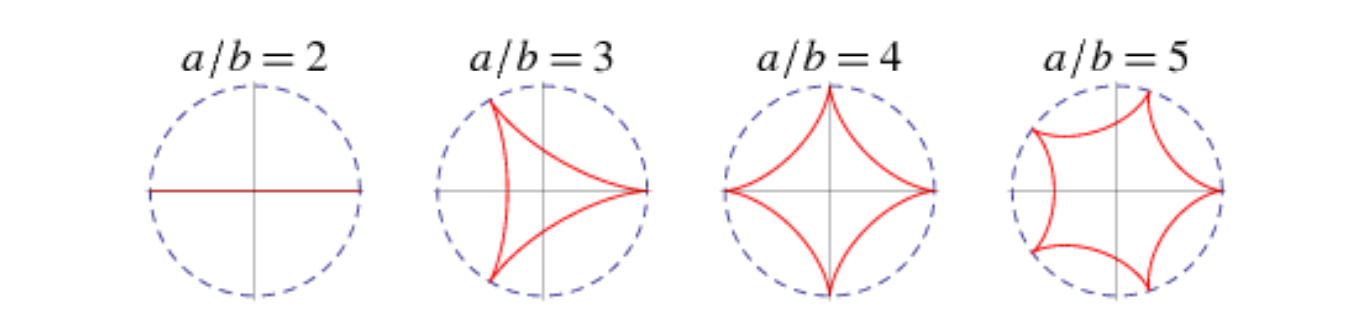
内旋轮线(内摆线):已知大圆半径为
特别的,由
当
-
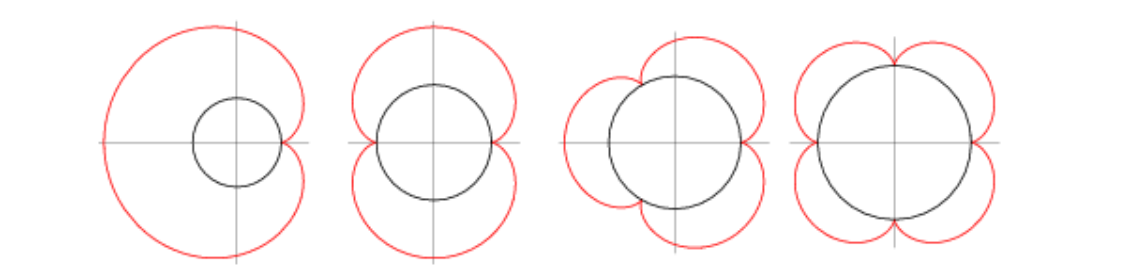
外旋轮线(外摆线):已知大圆半径为
2. 曲面的方程
1. 曲面方程的定义
- 曲面:具有某种特征性质的点的集合;具体说,曲面上点的特征性质也包含如下两方面要求
- 曲面上的点都具有这些性质
- 具有这些性质的点都在曲面上
2. 曲面方程的分类
- 曲面的一般方程
- 形式:
- 球面
- 实球面:
- 点:
- 虚球面:
- 实球面:
- 形式:
- 曲面的参数方程
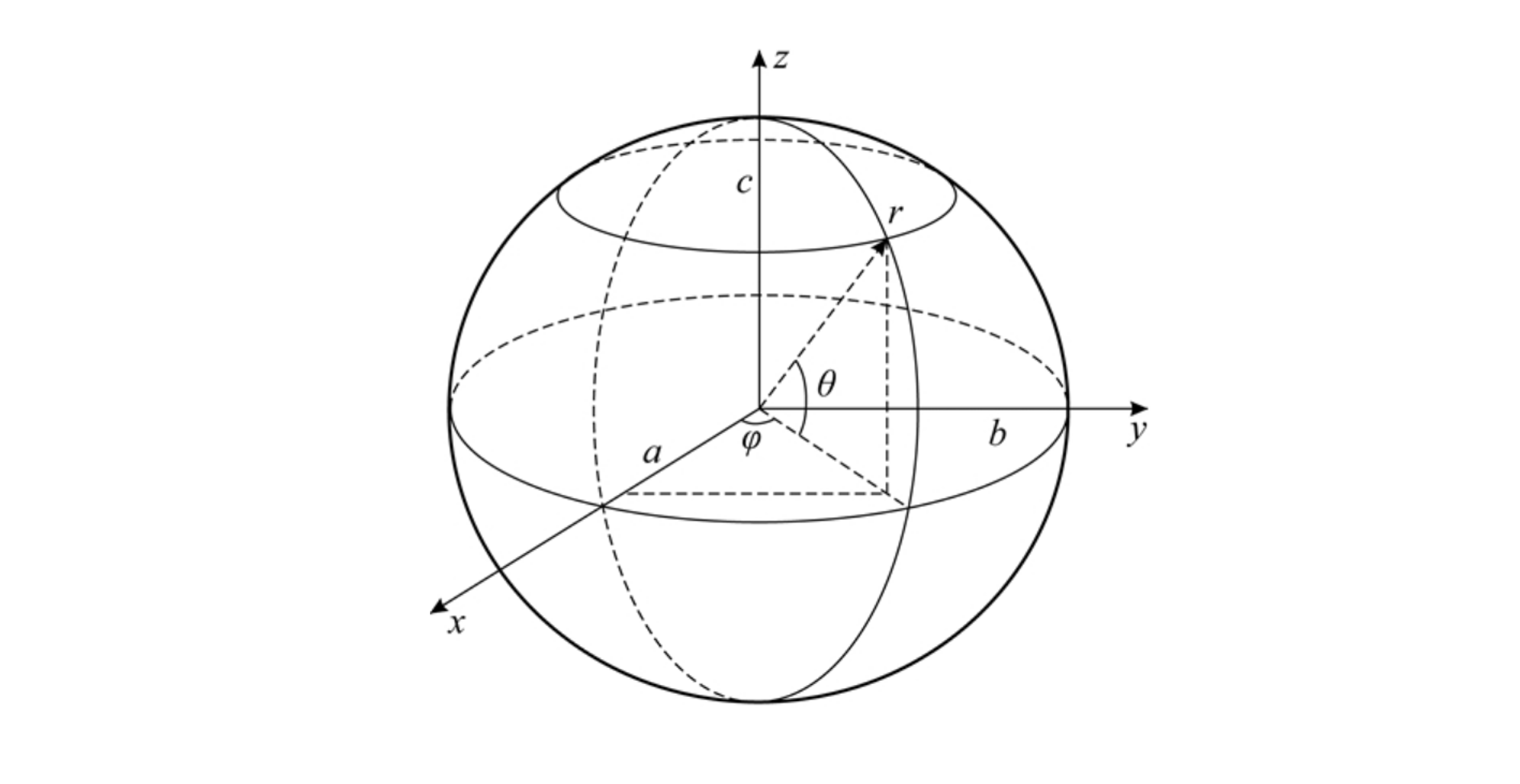
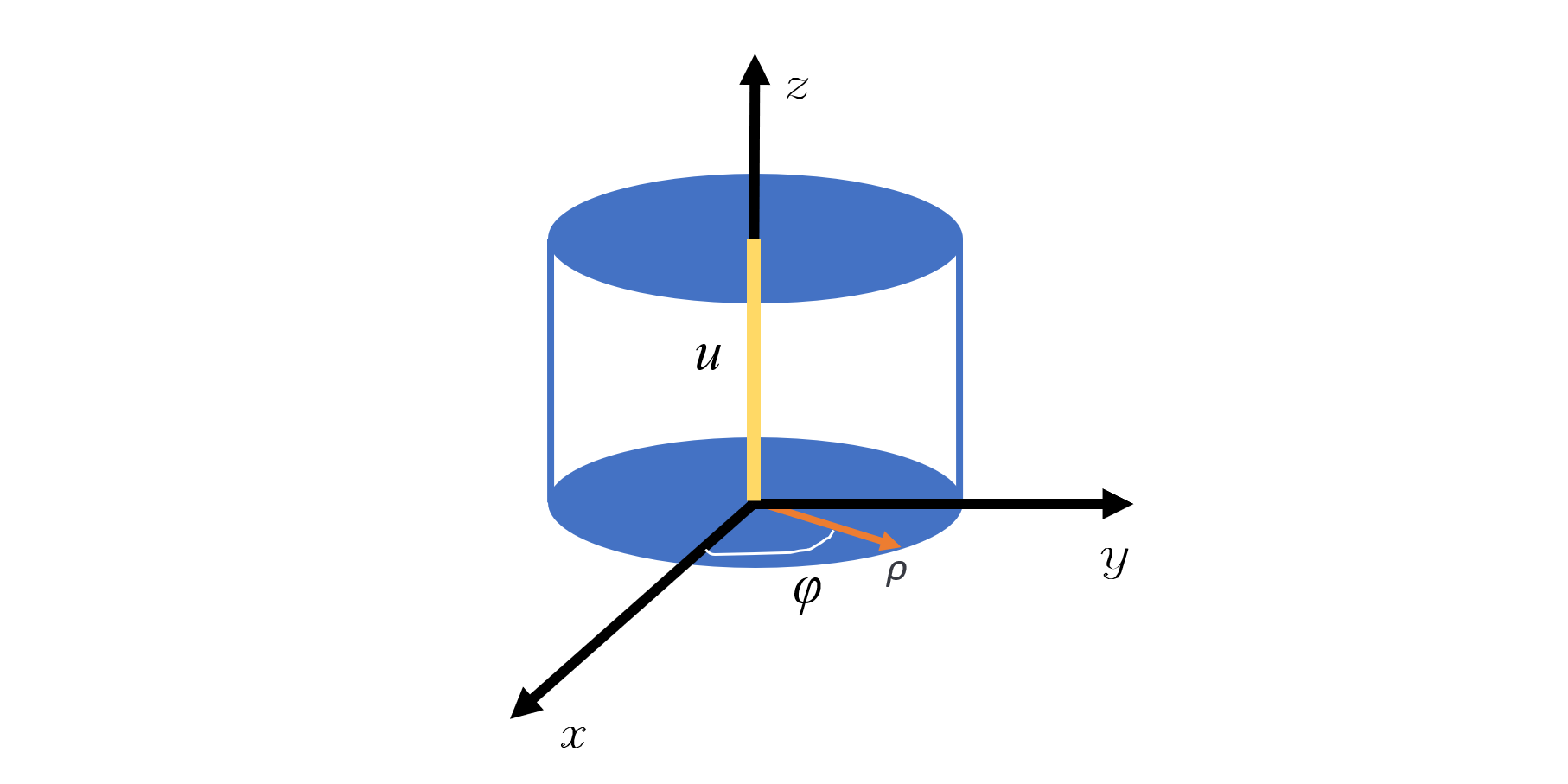
3. 球坐标系和柱坐标系
4. 二次曲面
3. 空间曲线方程
1. 空间曲线的一般方程
- 空间曲线:可以看作空间两个曲面的交线
2. 空间曲线的参数方程
- 向量式参数方程
- 坐标式参数方程
3. 空间曲线在坐标面的投影
- 投影柱面:设空间曲线的一般方程
- 投影曲线:空间曲线在
__EOF__
本文作者:RadiumGalaxy
本文链接:https://www.cnblogs.com/RadiumGalaxy/p/16915480.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
本文链接:https://www.cnblogs.com/RadiumGalaxy/p/16915480.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
标签:
Courses

 平面曲线、空间曲面和空间曲线
平面曲线、空间曲面和空间曲线
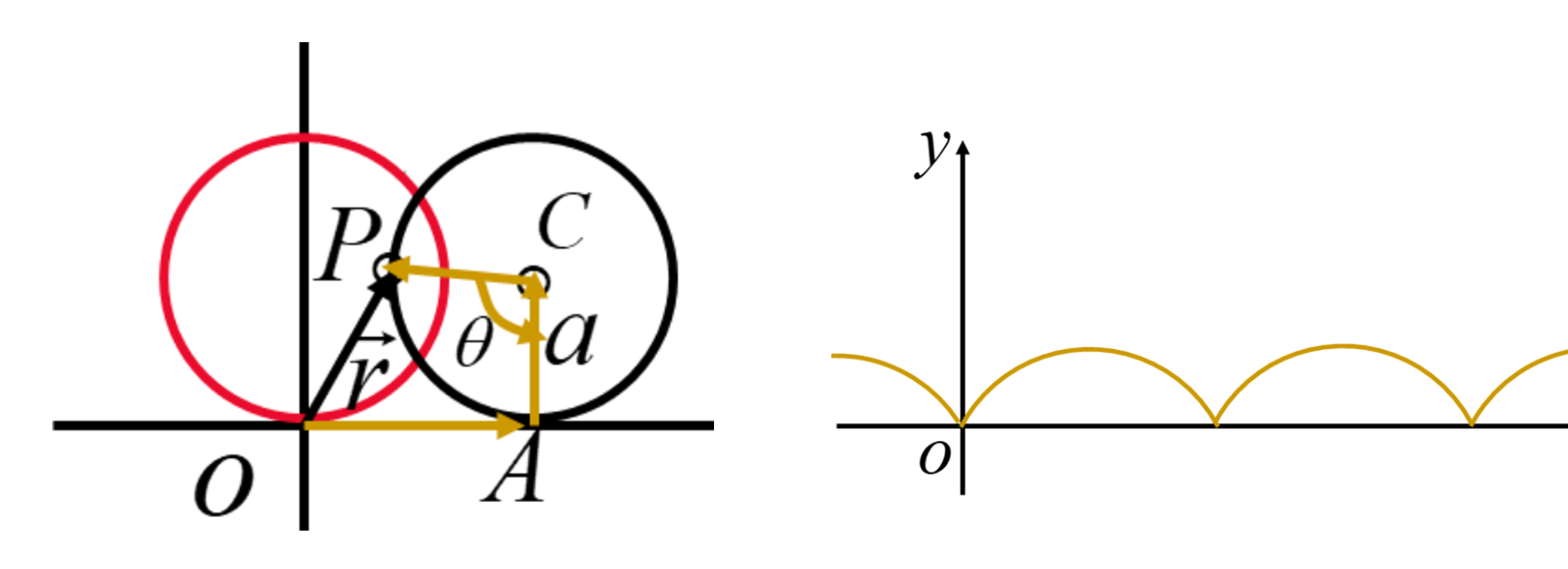



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!