03 计算机中的运算 | 计算机组成原理

1. 基本运算

1. 位运算

  1. 与&
    A B A&B
    0 0 0
    0 1 0
    1 0 0
    1 1 1
  2. 或|
    A B A|B
    0 0 0
    0 1 0
    1 0 0
    1 1 1
  3. 非~
    A ~A
    1 0
    0 1
  4. 异或^
    A B A^B
    0 0 0
    0 1 1
    1 0 1
    1 1 0

2. 逻辑运算

  1. 逻辑与&&
    A B A&&B
    0 0 0
    0 1 0
    1 0 0
    1 1 1
  2. 逻辑或||
    A B A||B
    0 0 0
    0 1 1
    1 0 1
    1 1 1
  3. 逻辑非!
    A !A
    1 0
    0 1
  4. 位运算与逻辑运算的区别
    1. 位运算针对二进制数，逻辑运算针对表达式的值
    2. 位运算的结果是二进制数，逻辑运算的结果是布尔量：真与假

3. 移位运算

  1. 算数移位：针对 有符号数
    1. 算术左移<<
      1. 高位移出，低位补0
      2. 溢出：如果移出的数字和新的符号位不相同，则溢出
    2. 算术右移>>
      1. 低位移除，高位补符号位
      2. 后果：会导致有效位数丢失
  2. 逻辑移位：针对 无符号数
    1. 逻辑左移<<
      1. 高位移出，低位补0
      2. 溢出：如果移除的是1，则溢出
    2. 逻辑右移>>
      1. 高位补0，低位移除
      2. 后果：会导致有效位数丢失

2. 加法与减法

1. 原码二进制加法

  1. 同号：数值位相加，如果最高位产生进位则表示溢出，和的符号取被加数的符号
  2. 异号：负数取补码，与正数相加，分两种情况讨论
    1. 最高数值位产生进位：符号位为0，表明加法结果为正，所得的数值位正确
    2. 最高数值位没有产生进位，符号位为1，表明加法结果为负，得到的是数值位的补码形式，需对结果求补，得到原码结果

2. 补码二进制加减法

  1. 加法
    1. 模2意义下，任意两数的补码之和等于该两数之和的补码：\([A+B]_{补}=[A]_{补}+[B]_{补} (mod 2)\)
    2. 加法规则：符号位参与直接相加
  2. 减法
    1. 模2意义下，两数差的补码等于被减数的补码加上减数的机器负数 ：\([A-B]_{补}=[A]_{补}+[-B]_{补} (mod 2)\)
  3. 溢出问题
    1. 为了处理溢出问题，在补码中采用两位符号位（变形补码）：\([x]_{补}=4+x(mod 4)\)
    2. 符号位仍然参与运算，但是表示的状态有所不同
      符号位 00 01 10 11
      状态 正数 正溢出 负溢出 负数

3. 移码二进制加减法

  1. 加法：直接将\([E_1]_{补}\)和\([E_2]_{补}\)进行模\(2^n\)相加，对结果符号进行 取反
  2. 减法：先将减数\([E_2]_{补}\)求补，然后与\([E_1]_{补}\)相加，对结果符号取反
  3. 溢出：如果两个数字的符号位相同，且与和数的符号位也相同（未对结果符号进行取反之前），说明发生了溢出

4. 加法器

  1. 串行进位加法器
    1. 分\(n\)步实现，每步只求一位和
    2. 缺点
      1. 进位按串行方式传递，速度慢
      2. 进位延时较长，时间复杂度\(O(n)\)
  2. 并行进位加法器
    1. 进位生成函数：\(G_i = A_iB_i\)
    2. 进位传递函数：\(P_i = A_i+B_i\)
    3. 进位表示：\(Carry_i = G_i+P_iC_{i-1}\)
    4. 缺点：高位的进位形成逻辑涉及变量较多，电路复杂
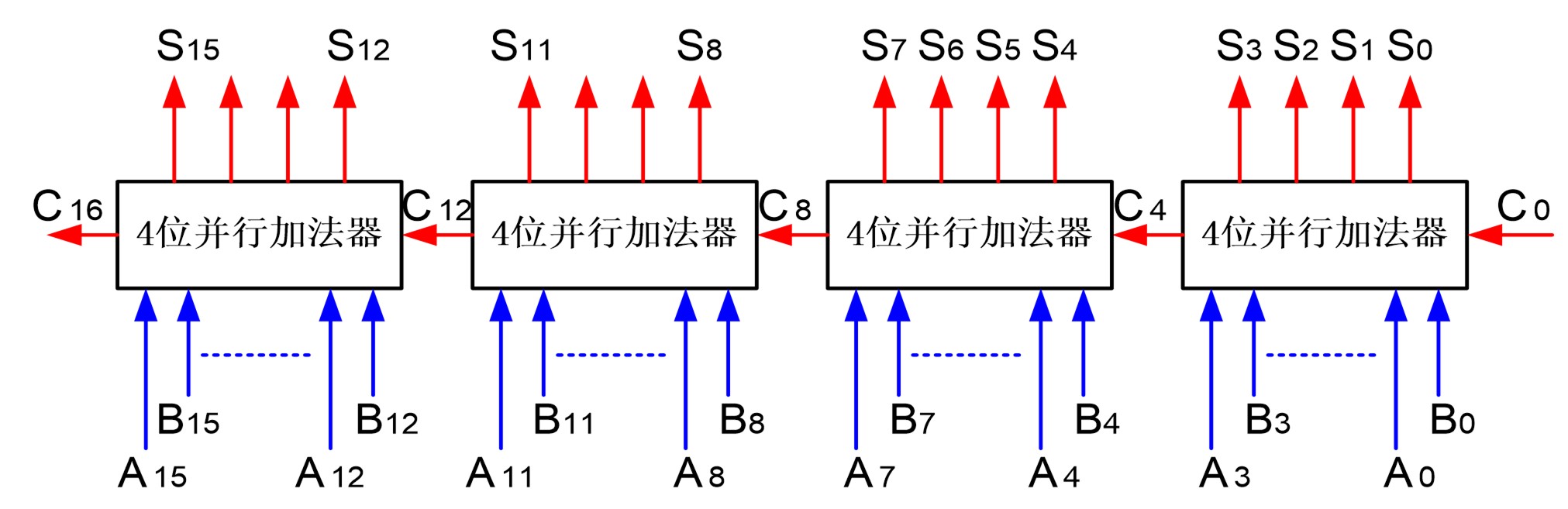
  3. 大规模加法器：组内并行，组间串行image

5. 浮点数的加法

  1. 对阶：目的是使两个操作数的阶码相等(对齐小数点)
  2. 规则：小阶向大阶看齐，阶小的数的尾数右移，右移位数等于两个阶码差的绝对值
  3. 步骤：对于规格化浮点数\(A = M_a\cdot 2^{E_a}, B = M_b\cdot 2^{E_b}\)
    1. 求阶差： \(E_a−E_b\)
    2. 对阶：\(M_b\cdot 2^{-(E_a - E_b)}\)
    3. 尾数相加：\(M_a + M_b\cdot 2^{-(E_a - E_b)}\)
    4. 结果规格化：\(A+B = (M_a + M_b\cdot 2^{-(E_a - E_b)})\times 2^{E_a}\)
  4. \(A\pm B = (M_a \pm M_b\cdot 2^{-(E_a - E_b)})\times 2^{E_a}\)
  5. \(A\times B= (M_a\times M_b)\times 2^{E_a + E_b}\)
  6. \(A\div B= (M_a\div M_b)\times 2^{E_a - E_b}\)

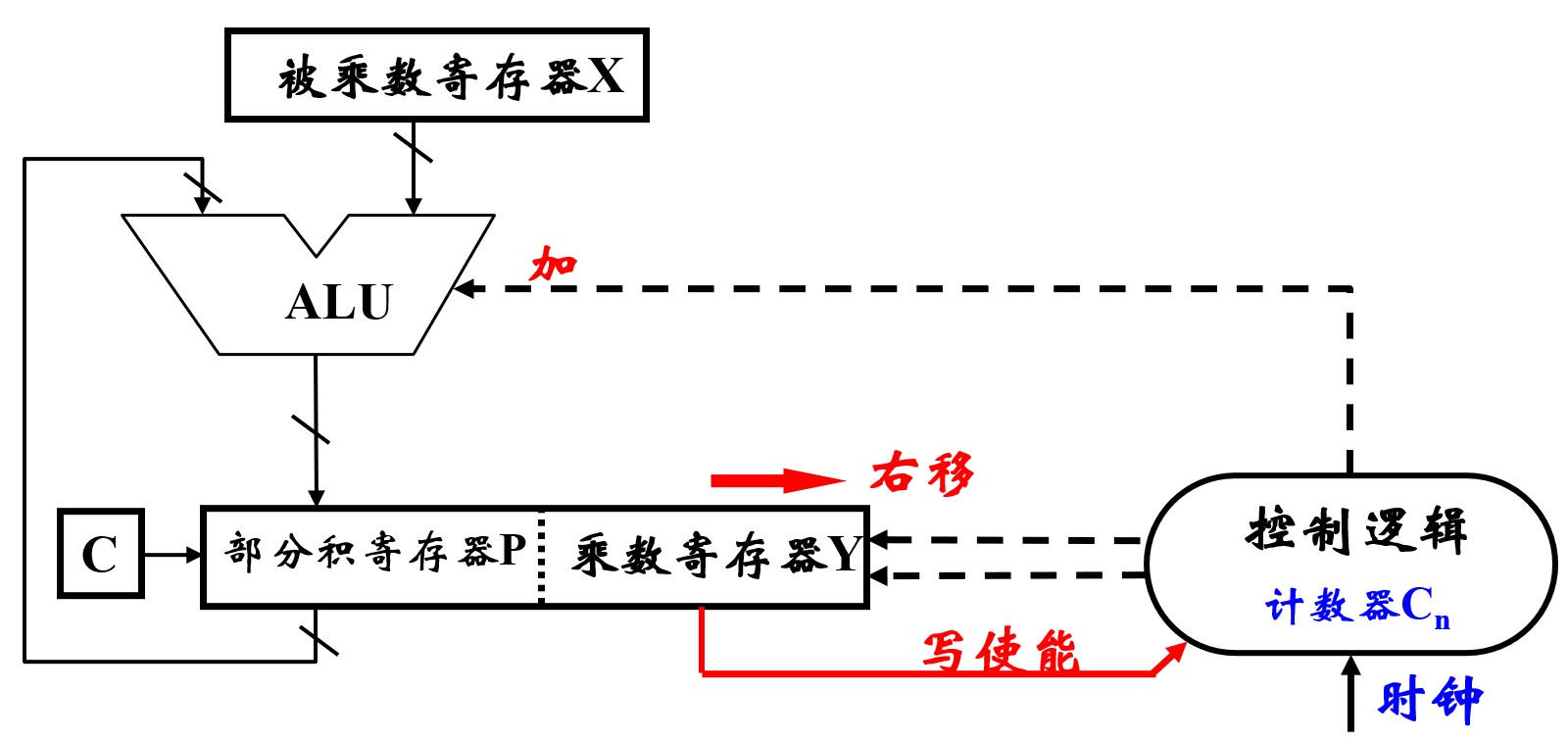
3. 乘法运算

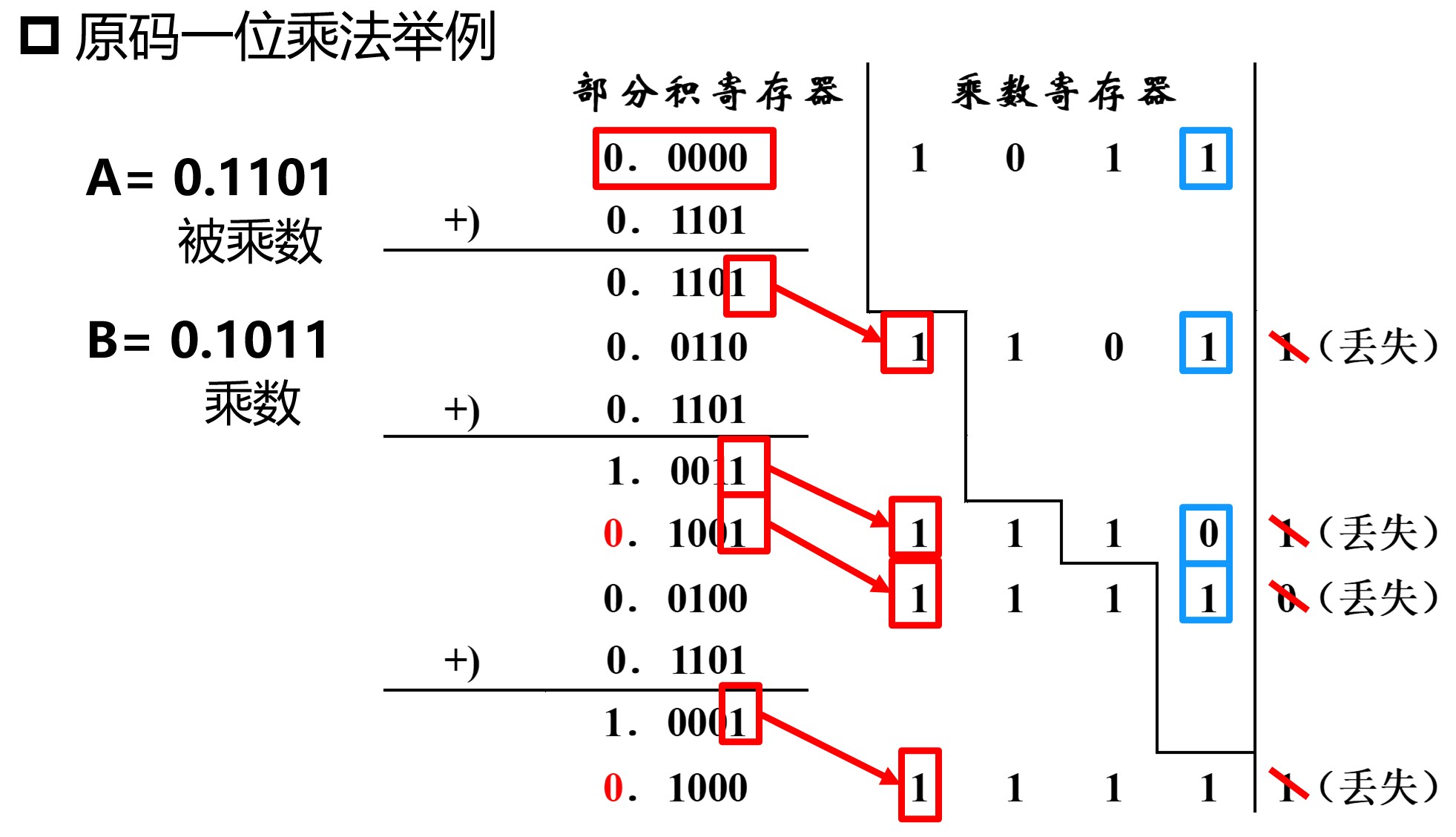
1. 原码一位乘法

  1. 组成部分image

    1. 部分积寄存器
    2. 乘数寄存器
    3. 加法器
    4. 控制电路

  2. 原理：每次循环对进位、部分积寄存器和乘数寄存器实现同步右移image

2. 补码一位乘法：\(Booth\)乘法

  1. \(Booth\)乘法：乘数和被乘数的符号位参与运算
  2. 判断
    判断位\((B_n,B_{n+1})\) 新部分积\([P_{i+1}]_{补}\) 操作 说明
    (0, 0) \(2^{-1}[P_i]_{补}\) \(\rightarrow 1\) 右移一位
    (0, 1) \(2^{-1}([P_i]_{补}+[A]_{补})\) \(+,\rightarrow 1\) \(+[A]_{补}\)右移一位
    (0, 1) \(2^{-1}([P_i]_{补}+[-A]_{补})\) \(-,\rightarrow 1\) \(+[-A]_{补}\)右移一位
    (1, 1) \(2^{-1}[P_i]_{补}\) \(\rightarrow 1\) 右移一位
  3. 运算规则
    1. 被乘数A和部分积P均取两位符号位即变形码，乘数取一位符号位，符号位参与运算
    2. 乘数末尾增设附加位\(B_{n+1}\) ，其初始值为\(0\)
    3. \(B_n\)和\(B_{n+1}\)构成各步运算的乘数判断位
    4. 按补码移位规则：部分积为正(第1符号位为0)，右移时有效位最高位补0；部分积为负，右移时有效位最高位补1
    5. 按\(Booth\)乘法表算法进行到第n+1步，但第n+1步的部分积不再移位
    image
posted @ 2022-10-25 16:21  RadiumStar  阅读(151)  评论(0)  编辑  收藏  举报