04 队列 | 数据结构与算法

1. 队列

1. 队列的概念

1. 队列：操作受限的线性表，只允许在一端进行元素的插入，另一端进行元素的删除
2. 空队列：不含有任何元素的队列
3. 队头和队尾：进行删除的一端叫 队头front，进行插入的一段叫 队尾rear

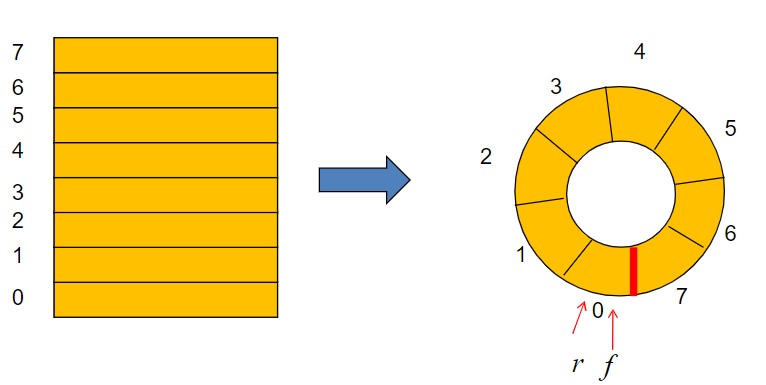
2. 队列的存储形式

1. 连续设计：利用一组连续的存储单元(一维数组) 依次存放从队首到队尾的各个元素，称为顺序队列
   1. 队头指针 总是指向队头元素的 前一个位置
   2. 操作

   #define MAXN 1000
   typedef struct queue{
       int queue_array[MAXN];
       int front, rear;
   }queue;
   

   // 1. initialize a queue
   void initialize(queue& q){
       q.front = q.rear = 0;
   }
   

   // 2. insert element in the queue
   bool push(queue& q, int data){
       q.rear = q.rear + 1;
       if(q.rear == MAXN) return false;    //overflow
       else {
           q.queue_array[q.rear] = data;
           return true;
       }
   }
   

   // 3. delete element in the queue
   bool pop(queue& q){
       if(q.empty()) return false;     // there's no element
       else {
           q.front = q.front + 1;  
           //会导致队列 *假溢出*（实际上还有空间）
           return true;
       }
   }
   

   // 4. check the queue is empty or not
   bool empty(queue& q){
       return q.front == q.rear;
   }
   

   // 5. return the top of the queue
   int front(queue& q){
       if(q.empty()) return -1;    //queue is empty
       else return q.queue_array[q.front + 1];
   }
   

2. 循环队列

   1. 定义：将为队列分配的向量空间看成为一个首尾相接的圆环；充分利用了向量空间，克服上述假溢出现象
      

   2. 操作

   #define MAXN 1000   //queue max size
   typedef struct queue{
       int queue_array[MAXN];
       int front, rear;    //full queue is (front+1)%MAXN == rear
   }queue;
   

   // 1. initialize a queue
   void initialize(queue& q){
       q.front = q.rear = 0;
   }
   

   // 2. insert element in the queue
   bool push(queue& q, int data){
       q.rear = (q.rear + 1) % MAXN;
       if((q.front + 1)%MAXN == rear) return false;    //overflow
       else {
           q.queue_array[q.rear] = data;
           return true;
       }
   }
   

   // 3. delete element in the queue
   bool pop(queue& q){
       if(q.empty()) return false;     // there's no element
       else {
           q.front = (q.front + 1) % MAXN;
           return true;
       }
   }
   

   // 4. check the queue is empty or not
   bool empty(queue& q){
       return q.front == q.rear;
   }
   

   // 5. return the top of the queue
   int front(queue& q){
       if(q.empty()) return -1;    //queue is empty
       else return q.queue_array[(q.front + 1) % MAXN];
   }
   

3. 链接设计
   1. 队列的链式存储结构简称为链队列，它是限制仅在表头进行删除操作和表尾进行插入操作的单链表。需要两类不同的结点：数据元素结点，队列的队首指针和队尾指针的结点
   2. 操作和单链表相似，只是多了front和rear队头队尾指针，并且操作限制在队头队尾

   typedef struct queue_node{
       int data;
       queue_node *next;
   }node;
   

   typedef struct queue{
       node *front, *rear;
       queue(node *front = nullptr, node *rear = nullptr):front(front), rear(rear){}
   }queue;
   

2. 其他操作受限的线性表

1. 输入受限的队列：限定在一端进行输入，可以在两端进行删除的队列
2. 输出受限的队列：限定在一端进行输出，可以在两端进行加入的队列
3. $Deque$双向队列：输入输出限定在两头的队列：限定在两端进行输出，在两端进行加入的队列

__EOF__

本文作者：RadiumGalaxy
本文链接：https://www.cnblogs.com/RadiumGalaxy/p/16796874.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！